网络型甩挂运输模式下的车辆调度问题

余 莉 林 桦 陈伯如

0 引 言

甩挂运输是指牵引车按照预定的运行计划，牵引车拖带挂车至目的地，在目的地点甩下所拖的挂车，换上其他挂车继续往另一个目的地的运输组织方式[1]。在甩挂运输实际运作中，牵引车与半挂车或挂车之间能够自由分离、耦合，通过两者之间的合理调度、接合，可以大幅度减少牵引车到达目的地后装卸货的等待时间，从而提高牵引车的运输效率。正因如此，甩挂运输成为我国道路运输的必然趋势[2]。

1 甩挂运输的组织模式

道路甩挂运输的组织模式主要有以下几种：一线两点、一线多点、一点多线和网络型甩挂四种模式。

1.1 一线两点甩挂运输

一线两点甩挂运输是在短途运输线路上采用的形式。牵引车往复于两装卸作业点之间，牵引车在线路两端根据具体条件作甩挂作业，根据货流情况或装卸能力，可采用“一线两点，一端甩挂”（即装甩卸不甩）和“一线两点，两端甩挂”。以“一线两点，两端甩挂”为例：设有A、B两个装卸作业点，A、B两点各预留一定数量的挂车。牵引车拖挂挂车从A点出发驶向 B点，到达 B点后，卸下挂车，挂上预留在 B点的挂车，驶向 A点。到达 A后卸下挂车，装上 A点挂车，进行下一循环。

1.2 一线多点甩挂运输

由一线两点的甩挂模式演化而来，装卸作业点在两个以上，所有装卸作业点由运输车辆串联。每个装卸点存在数量不等的半挂车，由单一的牵引车顺次在不同甩挂作业区进行甩挂作业。

1.3 一点多线甩挂运输

一点多线甩挂运输也是由一线两点的模式演化而来，所不同的是，一般其运输是单向的，即在一个完整的运输过程中（去程+回程），货物从集货点向货运站方向运输，或与之相反。因此在该模式下，牵引车去程是空载，回程是满载，或与之相反。

1.4 网络型甩挂运输

网络型甩挂模式是甩挂运输发展到一定阶段的产物，适合多个装卸作业点的长途运输。网络型甩挂运输的路线不一定是线性的，而是将整个运输线路有机地结合起来。网络中的各个装卸作业点可能对任何其他作业点产生货运需求。

2 车辆调度问题

车辆调度问题（Vehicle scheduling problem，简称 VSP）是运输管理研究中的核心问题之一。VSP一般描述为：对一系列客户（取、送货点），组织适当的行车路线使车辆有序地通过它们，在满足一定的约束条件（如货物需求量、发送量、交发货时间、车辆容量限制、行驶里程限制、时间限制等）下，达到一定的目标（如路程最短、费用极小、时间尽量少、使用车辆数尽量少等）[3]。

2.1 车辆调度问题的分类

车辆调度问题根据不同的标准可分为不同的类别[4]。根据车场（或货场、配送中心等）的数目分为单车场问题和多车场问题；根据运输车辆的种类多少可分为单车型问题（所有车辆容量相同）和多车型问题（车辆的容量不全相同）；根据车辆是否有容量约束，可分为有容量约束的车辆调度问题和无容量约束的车辆调度问题；根据载货现状可以分为满载车辆路径问题、非满载车辆路径问题；根据货运任务的完成是否有时间要求，车辆调度问题又可分为有时间窗约束和无时间窗约束的车辆调度问题；根据路径规划信息是否是一成不变，车辆调度问题可分为静态车辆调度问题和动态车辆调度问题。根据货运任务的性质，分为纯装货问题、纯卸货问题以及装卸货混合问题。

网络型甩挂运输网络中存在多个车场，牵引车拖挂挂车在各节点间进行作业，因此网络型甩挂运输模式下的车辆调度问题属于满载多车场车辆调度问题。

2.2 甩挂运输调度问题

甩挂运输的最大特点在于牵引车和挂车可以相互分离，其车辆调度问题也与传统车辆调度问题有所区别，这对车辆调度工作提出了新的要求。本文研究满载运输情况下的“一车一挂”甩挂运输车辆调度问题，文中将甩挂运输网络中的各个运输节点（如港口码头、物流园区、客户仓库等）视为牵引车的“服务点”，并假设这些服务点均有足够的空间存放挂车。

下面通过一个实际操作中的简单示例来说明这种甩挂运输的操作方法和调度过程。

（1）问题描述

假设在 2个车场和 5个服务点之间实行甩挂运输，2个车场编号分别是车场A和车场B；5个服务点编号分别是服务点 a、服务点 b、服务点 c，服务点d和服务点e。服务点a需要运1单位挂车货至服务点b，服务点b有1单位挂车货将根据货物类型运至服务点c或服务点d，服务点e要运2单位挂车货至服务点d。各服务点的运输需求和位置关系如图1所示。车场的空挂车数量不限，车场之间牵引车和挂车可以相互调用，牵引车实行“一车一挂”的甩挂运输，运输需求完成后，各服务点的挂车数目保持不变，牵引车返回车场。需要调度人员根据各服务点的货运需求和所拥有的车辆资源对这一系列任务进行调度。

图1 甩挂运输车辆调度示意Fig.1 Sketch map of drop and pull transport vehicle scheduling

（2）调度过程

第一阶段：先从距离服务点a最近的车场A派出牵引车1拖挂空挂车至服务点a，卸下空挂车，挂上服务点a事先装载好的送往服务点b的重挂车。同时从距离服务点e最近的车辆B派出牵引车2拖挂空挂车至服务点e，卸下空挂车后，挂上事先装载好的送往服务点d的重挂车。

第二阶段：牵引车1从服务点a将重挂车运至服务点b，卸下重挂、装上在服务点b的空挂车。牵引车2从服务点e将重挂运至服务点d，卸下重挂、装上在服务点d的空挂车。

第三阶段：牵引车1从服务点b将重挂运至服务点c，卸下重挂车，装上在服务点c或d的空挂车。

牵引车2从服务点d将空挂车运至服务点e，卸下空挂车，装上事先装载好的送往服务点d的重挂车。

第四阶段：牵引车1从服务点c或d将空挂带回车场A或B。

牵引车2从服务点e将重挂运至服务点d，卸下重挂车，装上在服务点d的空挂车。

第五阶段：牵引车2从服务点d将空挂车带回车场B。

牵引车的总路线流程为：

牵引车2：

该问题的车辆调度如图1所示。

3 网络型甩挂运输车辆调度问题的数学建模

3.1 问题描述

甩挂运输车辆的调度问题可以描述为：

某个运输系统里分布有多个车场和多个服务点，牵引车只能停放在车场，每个车场可提供的牵引车和空挂车数量不限，车场之间的牵引车和挂车资源共享，但牵引车运输不可以从车场到车场。服务点有足够数量的空挂车，服务点之间的挂车可以通用，但服务点自身拥有的挂车数保持不变。为满足服务点之间的货运需求，在甩挂运输的模式下，牵引车从车场出发向多个服务点执行配送任务，在有限时间内完成货运需求后返回车场，如何安排牵引车合理的配送路线，使得总运输成本最小。

（1）已知条件

①车场与服务点之间的往返路线不一定对称，运输网络中各个车场及各服务点之间的距离固定。②用单位挂车作为两点间的货运需求量的单位。③多个车场服务多个服务点，且车场能提供牵引车和挂车的数量不限。

④牵引车行驶路线的起点和终点均为车场，但牵引车不可从车场直接行驶到车场。

⑤客户自身拥有足够数量的空挂车，所有待运货物都在牵引车到来之前装上，客户间的挂车可以通用，但客户拥有的挂车数量保持不变。

⑥牵引车卸挂和装挂的作业时间较短，忽略不计。⑦牵引车以固定的平均行驶速度进行运输作业。（2）优化目标

单目标：总运输成本最低。

3.2 模型构建

3.2.1 建模说明

为了满足服务点i到服务点j之间的货运需求，首先牵引车从距离服务点 i最近的车场或服务点出发，将空挂车送至服务点 i，换上重挂后将重挂运至服务点 j。到达服务点 j之后，卸下重挂，换上服务点j的空挂车，如无服务，则牵引车挂上空挂返回最近车场；如有服务，则挂上空挂驶向另一个服务点。整个运作过程中，牵引车运输作业不产生等待时间。

由以上描述可知，对于甩挂运输网络中的每一个节点，为完成货运需求都需要牵引车到达和离开该节点。

牵引车的行驶状态分为两种类型：

①h=1：牵引车拖挂空挂车行驶；

②h=2：牵引车拖挂重挂车行驶。

对于每个服务点而言，可能是牵引车拖挂空挂或重挂到达，也可能是牵引车拖挂重挂和空挂离开。对于车场，牵引车到达和离开都只能是拖挂或空挂状态。牵引车拖挂空挂和重挂的单位成本不同。

3.2.2 数学模型

（1）变量设置：

D：所有车场的集合, D =｛ 1， 2， 3，…, d｝；

C：所有服务点集合， C =｛ 1， 2， 3， … , c｝；

V：所有牵引车的集合， V =｛ 1， 2， 3， … , v｝；

H：牵引车的行驶状态集合， H ={1， }2；

d：第d个车场；

v：第v辆牵引车；

lij：点i到点j的距离（km）；

Qij：点i到点j的货运量（挂车）；

C(h)：牵引车行驶状态为h时的单位成本（元）；

T：完成所有货运需求的最大工作时间（h）；

S：牵引车平均行驶速度（km/h）；

（2）建立模型

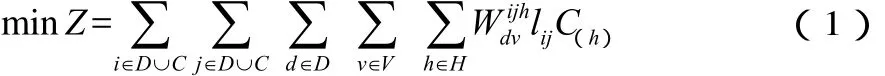
s.t.

式（1）表示模型的目标函数是实现总运输成本最小。

式（2）表示牵引车拖挂重挂从服务点 i到服务点j行驶的次数等于服务点i到服务点j的运输需求；

式（3）表示每个服务点挂车数不变；

式（4）表示牵引车拖挂重挂到达服务点 i的总和等于其他各服务点到服务点i的货运量的总和；

式（5）表示牵引车拖挂重挂离开服务点 i的总和等于服务点i到其他各服务点的货运量的总和；

式（6）表示牵引车只能拖挂空挂从车场出发；

式（7）表示牵引车只能拖挂空挂返回车场；

式（8）表示牵引车不能直接从车场到车场；

式（9）表示所有货运需求必须要在牵引车有限工作时间内完成。

4 算法设计

4.1 算法思想

根据各服务点的货运需求，将服务点之间连成有向图，并根据货运量大小赋予权值。一辆牵引车完成一个有向图；若完成该有向图的时间超过设定的最大牵引车工作时间，则该有向图分解成若干个有向图，由不同的牵引车完成。当牵引车到达有向图中最后一个服务点时，根据距离大小，判断是返回最近的车场还是继续完成下一个有向图的任务，直到所有任务完成。

4.2 算法步骤

步骤1：初始化集合；

步骤2：更新各服务点参数（货运量、挂车数量）；

步骤3：将各服务点根据货运需求连成有向图，权值为货运量（货运量以挂车为单位）。

步骤4：判断有向图中各服务点的货运需求所需时间是否会超过牵引车的最大设定工作时限，lij计算（2n-1）次，其中 n为有向边的权值。若未超过设定时限，执行步骤5；否则，执行步骤7。

步骤5：选定离有向图起点最近的车场。

步骤 6：判断离有向图止点最近的车场的距离1l和离该止点最近的另一个有向图起点的距离2l的大小关系：若12ll≤，选定车场，执行步骤10；否则，执行步骤9。

步骤7：将该有向图进行分段，最大的不超过设定时间的部分，执步骤行8；剩余部分，执行步骤4。

步骤8：寻找离有向图起点最近的车场和离有向图止点最近的车场，执行10。

步骤9：将有向图止点与寻找到的有向图起点连接，执行4。

步骤 10：将选定的起止车场和有向图连接，形成线路。

步骤 11：判断是否还有服务点未与车场形成线路，若是，执行步骤2；否则，任务结束。

具体算法流程参见图2。

4.3 算例分析

假设在一个有13个节点的网络中，有3个车场，在运输系统的编号分别为车场A、车场B、车场C；10个服务点在运输系统的编号分别为服务点1、服务点2、服务点3、服务点4、服务点5、服务点6、服务点7、服务点8、服务点9、服务点10。各节点之间相互距离以及货运需求如表1、表2所示。在这10个客户点之间随机生成货运需求，并假设牵引车每天最大工作时限为 24小时，牵引车行驶平均速度为60km/h。牵引车从车场出发满足客户点之间货运需求后，返回最近车场，目标是使得牵引车的总行程最小。

图2 甩挂运输车辆调度的算法流程Fig.2 Algorithm process of drop and pull transport scheduling

表1 运输网络中各节点间的距离（单位：km)Tab.1 Distances between each node in the transportation network（unit: km）

表2 客户点之间的货运需求（单位：挂车）Tab.2 Freight demands between customers（unit: trailer）

（1）根据货运需求形成初步有向图，并对每边赋予权值，标注节点间距离：

（2）根据有向图生成原则，有向图调整为：

（3）根据各有向图起止点选定起止车场，连成牵引车行驶路线：

4.4 实验结果

假设各服务点之间是高速公路对接的，设牵引车行驶平均速度为 60km/h；一般情况下，可设装货时间为1.5h/挂，卸货时间为1h/挂；设牵引车重载行驶的成本为0.5元/km，空载行驶的成本为0.35元/km；在牵引车每天最大工作时限为24小时的情况下，传统运输模式和甩挂运输模式有不同的运输结果，如表3所示。

由表3可知，甩挂运输能有效地减少汽车空载行程，提高运输效率；由于甩挂运输不产生等待时间，能够有效地减少工作时间，且运距越短，节约时间的效果也越明显。

表3 传统运输模式和甩挂运输模式的实验结果分析Tab.3 Experimental result analysis of the traditional transport and drop-pull transport

5 结束语

甩挂运输作为一种高效的运输方式，已经在国内外多地得到广泛的应用。研究其车辆调度问题，有助于更好地发挥降低物流成本，促进节能减排、提高经济效益的优势。有关甩挂运输车辆调度的研究还不多，本文只是进行了初步的探索和研究，如一车多挂和动态情况下的甩挂运输等的车辆调度还值得进一步研究。

[1] 吴 宇, 曾传华, 杨 伟. 道路运输组织甩挂运输策略研究[J]. 物流工程与管理, 2010,(08): 83-85.

[2] 温旖旎. 道路运输发展的必然趋势[J]. 现代经济信息(产业经济), 2012,(3): 273

[3] 肖建军. 车辆路径优化文献综述[J]. 广东技术师范学院学报(自然科学版), 2010,(2): 31-36.

[4] 陈君兰, 叶春明. 物流配送车辆调度问题算法综述[J]. 物流科技, 2012,(3): 08-12.

[5] 王 莹. 拖挂分离模式集装箱运输车辆调度研究[D]. 武汉：武汉理工大学, 2010.

[6] 熊 浩. 多车场物流配送车辆调度研究[D]. 武汉：华中科技大学, 2006.