多品种流交通网络的最大流算法研究
2014-03-21崔皓莹寇玮华
崔皓莹 寇玮华 丁 振
0 引 言
交通网络中的最大流量的分配问题,通常是针对单一品种的流量分配,在保持流量约束与守恒的条件下,一般选择基于Ford-Fulkerson算法对流量进行调整,以达到交通网络的最大流状态[1-10]。但在实际应用中,多品种流的最大流分配常常会在交通网络中出现,但是,针对于多品种流的研究成果却很少,因此,本文在借鉴传统的网络流理论及算法的基础上,构建了可行的多品种流交通网络最大流分配算法。
本文首先介绍多品种流交通网络问题并对其进行分析,在保证流量约束的条件下,基于 Ford-Fulkerson算法的思路,构造多品种流交通网络的最大流算法,在保证网络流量分配为最大流的状态下,明确每一个品种在网络中的流量分配。
1 多品种流交通网络的引例
为了解释说明交通网络的多品种流问题,也为了清晰地阐述多品种流交通网络最大流分配的算法研究,先给出多品种流交通网络的一个引例。
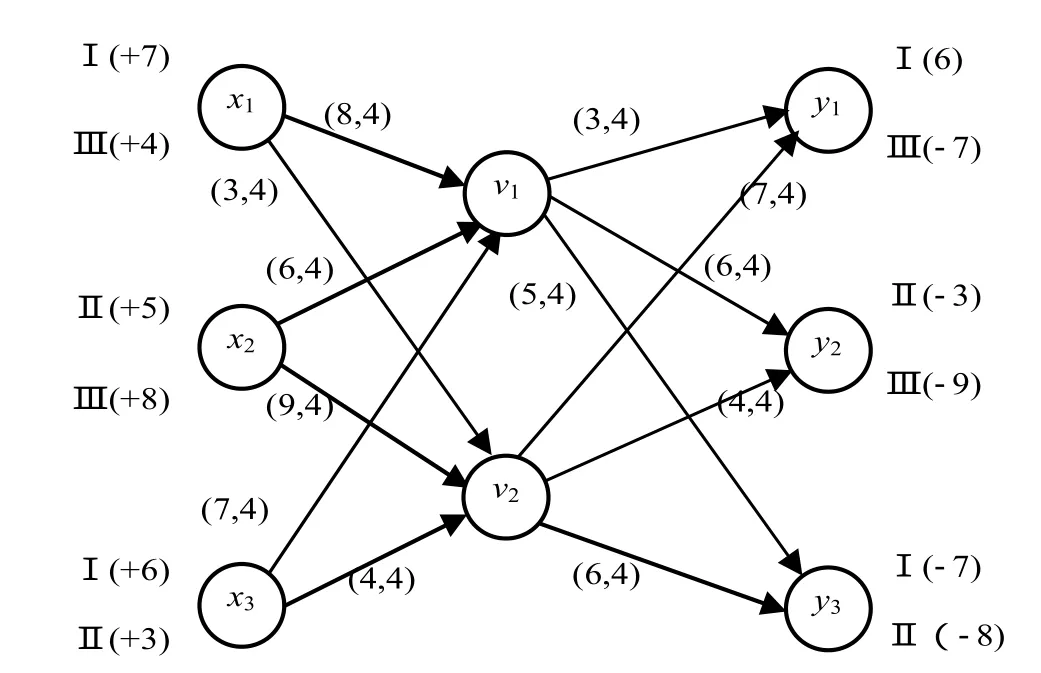
图1 交通网络的引例Fig.1 An example of transportation network
引例 有交通网络如图1所示,它分别给出了运送能力和运送费用,即边的容量、费用。其中 x1生产Ⅰ和Ⅲ两种产品,数量分别为7 t和4 t;x2生产Ⅱ和Ⅲ两种产品,数量分别为5 t和8 t;x3生产Ⅰ和Ⅱ两种产品,数量分别为 6 t和 3 t。y1、y2、y3分别为三个需求地,y1需要Ⅰ和Ⅲ两种产品,需求量分别为6 t和7 t;y2需要Ⅱ和Ⅲ两种产品,需求量分别为 3 t和9 t;y3需要Ⅰ和Ⅱ两种产品,需求量分别为7 t和8 t。
针对此引例,传统的交通网络最大流分配算法就不能完全适用于多品种交通网络的流量分配问题,所以,有必要研究多品种流交通网络的最大流分配算法。
2 多品种交通网络的最大流分配研究
2.1 多品种交通网络最大流问题分析
给定交通网络 G=(V,E,C,F,W,X,Y ),其中V=(v1,v2,…,vn),E=(e1,e2,…,em)。对顶点集合 V 取定两个非空子集X、Y。X为只发出流量的顶点集合,Y为只接收流量的顶点集合,且X∩Y=Ø。把X中的顶点xi称为网络G的源,Y中的顶点yi称为网络G的汇。针对边ei赋予两个非负的整数参数cij、fij,分别为边(vi,vj)的容量、流量。设顶点vi∉X、Y,即vi为中间点,用f+(vi)表示顶点vi发出的流量之和,f-(vi)表示顶点vi接收的流量之和。设k为多品种流中的第k个品种流,其中k=1,2,…,q。fijk为第k个品种流在边(vi,vj)上的流量,f+(vik)表示顶点vi发出第k个品种流的流量之和,f-(vik)表示顶点vik接收第k个品种流的流量之和。
针对多品种交通网络图,边(vi,vj)要遵从两个约束条件:
(2)所有中间点vi都要遵从流量守恒条件,即在保证所有品种的总流量守恒的同时,也要保证每一个品种的分流量守恒,则有:
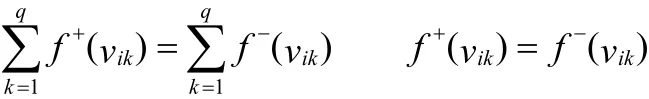
基于以上分析,多品种交通网络的最大流分配模型如模型(1)所示:

2.2 最大流算法思路
基于Ford-Fulkerson算法的思路,本文针对于多品种交通网络问题设计了其最大流算法。先将多源多汇的交通网络图G,化为单源单汇形式的网络图Gn,边(vi,vj)的属性为容量、流量,设表现形式如下,,式中,fij表示边(vi,vj)的总流量;fijk表示各品种的分流量。再给定网络图Gn一个初始的可行流 f(也可以是零流),对结点进行标号,判断和寻找是否存在增流链,如果不存在,则当前网络已为最大流,算法停止;如果存在增流链,再根据其调整值,调整网络,直至没有赠流链,算法停止。
针对最大流算法,设计结点vj的标号形式如下:[vi,边的方向,lk(vj)],其中,vi表示被标号点 vj的前一个顶点;边的方向通过“+”或“-”表示前向边或后向边;lk(vj)表示增流链中针对于k品种的调整量。
2.3 最大流算法步骤
算法步骤如下:
第一步 将 G转换为单源单汇的结构形式,构建新的网络图Gn:
(1)单源的构建
① 基于所有源xi共有的品种数q,在G中设定q个新源xk,同时将顶点xk与生产k品种的顶点xi相连,构建出边(xk,xi)。该边的容量c(xk,xi)等于网络G的源xi所生产的第k个品种的数量。
② 设定 x作为单源,同时构建边(x,xk),该边的容量 c(x,xk)=∑c(xk,xi)。
(2)单汇的构建
① 基于所有汇 yi共需要的品种数 q,在 G中设定 q个新汇 yk,同时将接收 k品种的顶点 yi与顶点yk相连,构建出边(yi, yk)。该边的容量c(yi, yk)等于交通网络G的汇yi所需要的第k个品种的数量。
② 设定y作为单汇,同时构建边(yk, y),该边的容量 c(yk, y)=∑c(yi, yk)。
第二步 设集合 X={x, xk, xi︱k=1,2,…,q;i=1,2,…,n}、V={vi︱i=1,2,…,n}、Y={yi, yk, y︱k=1,2,…,q;i=1,2,…,n },并给定网络图Gn一个初始流(一般为零流),即初始的均为,设源x的增流量l(x)= +∞,可以对源x标号为(0,+,+∞)。
第三步 对与x有直接连线的顶点xk标号,其中边(x, xk)为前向边。若fxk=cxk,此时该边流量不能增加,那么不对xk标号,即不能对k品种进行流量调整;若fxk<cxk,此时流量能增加,存在 lk(vx)=min{l(x),cxkfxk},那么,顶点xk标号为[x,+,lk(vx)],可判断出此时是对该路径的k品种进行流量调整。
第四步 继续检查,判断之后的边(vi,vj)能否成为增流链的边,边(vi,vj)成为增流链中的边必须满足如下条件:
(1)当vj∈X,V时,判断边(vi, vj)是否为增流链中的边,分以下两种情况:
① 当边(vi, vj)为前向边时:若 fij<cij,则该边流量可以增加,边(vi,vj)为增流链中的边,那么,lk(vj)=min{lk(vi),cij-fij},且顶点 vj标号为[vi,+,lk(vj)];若 fij=cij,则该边流量不可以增加,即不对顶点 vj标号。
② 当边(vi, vj)为后向边时:若fij>0,则该边流量可以减少,边(vi,vj)为增流链中的边,那么,lk(vj)=min{lk(vi), fij, fijk},且顶点 vj标号为[vi, -, lk(vj)];若fij=0,则该边流量不可以减少,即不对顶点vj标号。
(2)当 vj∈Y时,判断边(vi, vj)是否为增流链中的边,分以下情况:
① 当 vj∈yi时,设 vm为 yi的前一个顶点,判断边(vm,yi)是否为增流链中的边,方法同上。
② 当 vi∈yi,vj∈yk时,判断边(yi,yk)是否为增流链中的边,分以下两种情况:
♦ 顶点 yi与顶点 yk有直接连线,则判断边(yi,yk)能否成为为增流链中的边,若边(yi,yk)为增流链中的边,那么对顶点 yk标号,若边(yi,yk)不为增流链中的边,那么不对顶点yk标号。具体方法同上。
♦ 顶点 yi与顶点 yk没有直接连线,则边(yi,yk)不为增流链中的边,那么不对顶点yk标号。
若顶点 yk被标号,则转第五步;若顶点 yk没被标号,说明此路径无法找到一条增流链,返回第三步重新寻找增流链。
第五步 当汇y被标号,那么说明存在增流链,此时,按照标号方式的第一项,从汇y进行反向追踪,可得到增流链Q,以及调整量lk(Q)=lk(y)。流量的调整按照以下规则进行:
(1)边(vi, vj)在增流链中为前向边时,边的流量调整为,其余品种的流量保持不变。
(2)边(vi, vj)在增流链中为后向边时,边的流量调整为,其余品种的流量保持不变。
第六步 返回第三步,不断循环,直到不能找到增流链为止,即此时网络已为最大流,同时可确定多品种流交通网络 Gn在最大流情况下,各品种的流量分配方案。
2.4 示例求解
为了更好地解释说明多品种交通网络的最大流分配问题,下面对引例进行求解。
第一步 将图 1的交通网络转换为单源单汇的网络图Gn,并给Gn一个初始流,给定源x标号(0,+,+∞),如图2所示,边旁数据依次表示容量、流量。
第二步 利用标号法寻找从源x到汇y的一条增流链 x→xI→x1→v1→ y1→y,lI(Q)=min{13,7,8,3,6,13}=3,该增流链包含边(x,xI),因此是对I品种增流,按照 Ford-Fulkerson算法的思路调整流量,如图 3所示。
第三步 反复迭代寻找增流链,对其对应品种进行流量调整,其余步骤省略,最终的结果如图4所示。
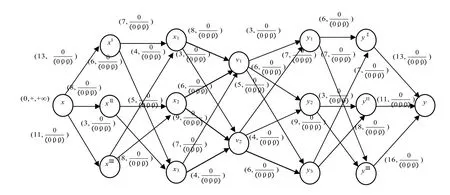
图2 交通网络的初始流Fig.2 Initialization flow of the transportation network

图3 第一次流量分配Fig.3 First flow distributing of the transportation network

图4 最大流分配方案Fig.4 Maximum flow distribution scheme
通过以上步骤,由图4可以知道该引例的总体方案,也可以知道该引例各个品种的具体方案。交通网G的最大流 max z=8+3+3+9+3+4=30,同时可知 x1发出Ⅰ品种7 t、Ⅲ品种4 t;x2发出Ⅱ品种5 t、Ⅲ品种7 t,x3发出Ⅰ品种5 t、Ⅱ品种2 t。
3 结束语
本文通过对多品种交通网络进行分析,并将多源多汇网络图构建成单源单汇的网络图形式,再基于Ford-Fulkerson算法在交通网络中寻找增流链以及流量调整的思路,设计了适合于多品种交通网络的最大流算法,并通过示例对算法进行了验证。然而,在交通网络中,仍然存在许多问题需要研究。一个多品种交通网络的最大流的流值是一定,但分布的状态不同,因此,最大流的分配方案是多种多样的,那么,也许就会存在特定的产地或销地有着具体的流量要求的情况下,求解多品种交通网络的流量分配问题,又或者在多品种交通网络中的中间点有截流的情况下,对该网络进行流量分配,这些问题都有待以后的研究。
[1] 寇玮华 编著, 李宗平 主审. 运筹学[M]. 成都:西南交通大学出版社,2013.
[2] 甘爱英等. 运筹学[M]. 北京:清华大学出版社,2002.
[3] 寇玮华,崔皓莹. 满足交通网络流量增长态势的扩能优化研究[J]. 交通运输工程与信息学报,2012,10(4):19-25.
[4] 寇玮华,董 雪,吕林剑. 交通运输网络中两个结点间有流量约束的最小费用最大流算法[J]. 兰州交通大学学报,2009,28(6):104-109.
[5] Network Optimization.麻省理工学院开放课件[EB/OL]. http∶//www.core.org.cn/OcwWeb/index.htm,2003.
[6] Transportation Flow System.麻省理工学院开放课件[EB/OL]. http∶//www.core.org.cn/OcwWeb/index.htm,2002.
[7] 谢 政,汤泽滢. 带模糊约束的最小费用流问题[J].模糊系统与数学,1999,13(2)∶ 90-941.
[8] 程 琳,王 炜. Dial交通量分配模型和选择率问题的研究[J]. 交通运输系统工程与信息,2002,2(3):29-32.
[9] 陈光亚. 带有向量值费用函数的交通网络平衡问题——模型与分析[J]. 交通运输系统工程与信息,2006,6(5):56-58.
[10] 任 刚,王 炜. 可直接计算转向流量的改进型Dial交通分配算法[J]. 中国公路学报,2005,18(4):83-86.
