对含有向量因子的曲线方程之三类问题的探讨

汪家军

(襄阳职业技术学院汽车工程学院，湖北襄阳441050)

求曲线方程在高考和数学竞赛中是公认的压轴题。命题专家们常常将向量因子寓于高考题的求曲线方程中作局部条件，借其宽阔的知识网点，灵活的构造方法和广泛的应用范围，来考查学生的空间想象能力、数学运算能力、动态思维能力和创新能力;或将其与其它形式的数学问题交融起来，检验学生分析解决问题的能力［1］;本文对含有向量因子的曲线方程之三类问题进行了探索，以期合理分类、探求共性、寻求规律，以求抛砖来引玉。

1 点积类问题

问题解析:对于点积类问题，可以以坐标系为依托让已知条件中的向量获得解放，再用其属性把向量表示翻译成几何性条件借以激活已知条件中的向量因子，紧扣方程思想和向量的数积运算规律及几何特性，就可依势而为。

(1)若一条双曲线的中心为O，其一个焦点为F，该双曲线的一侧经过点Q，(如图1所示)，且试求当取得最小值时此双曲线方程。

(2)设P、T为动点，分别在如上(1)求出双曲线的两条渐近线上运动，又设F1为这组双曲线的左焦点，当5|PT|=2|F1F|时，请求出线段PT的中点M的运动轨迹的方程，并说明该轨迹是何种曲线。

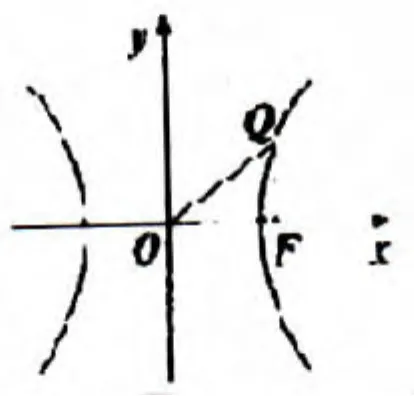
图1

解:(1)此时问题的条件含向量的点积与向量的模，依据激活向量因子的方法可以先设所求的双曲线方程为，再设点 Q 为(x1，y1).

(2)此时问题(1)已经解决了曲线方程问题，只要在此基础上再活化其特别条件下即可。设A(x1，y1)，B(x2，y2)，l1的方程为，l2的方程为

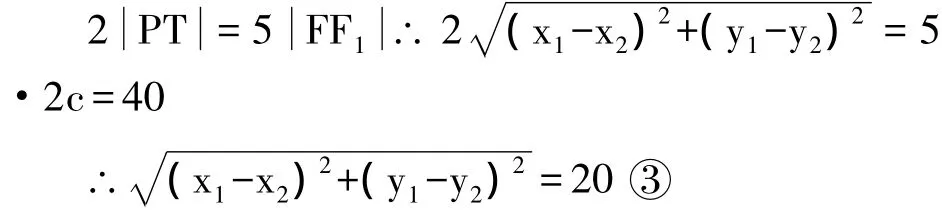
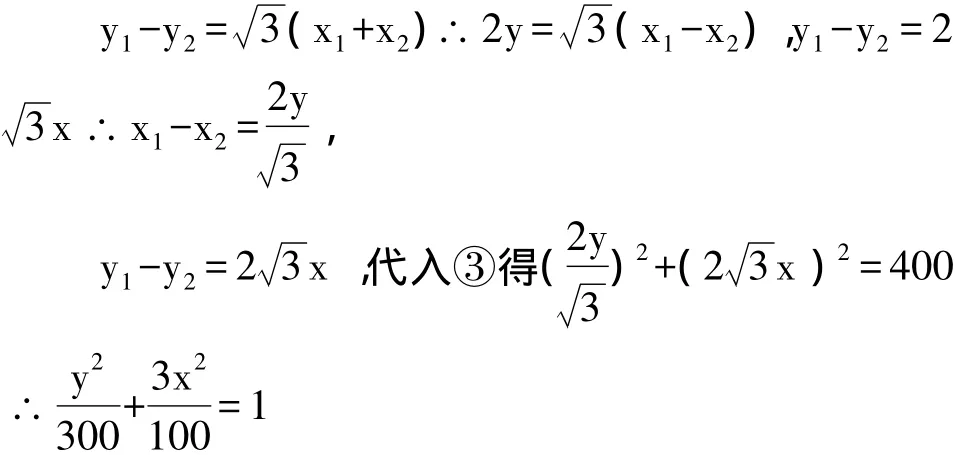
由此可知，点M的轨迹是焦点在y轴上的椭圆。

2 转移类问题

问题解析:这类题的设计是通过信息转移的方式来传导解题思路。在适当的坐标系下，点就会转化为向量从而获得活力，也就是构造了相关向量。因此，只要在坐标系下将点转化为向量，再建立与其等价的代数式即可求解。另外，当第⑴小题的问题得到解决之后，再将这一结论作为下一问题的已知条件的一部分，设计与上一个问题有关的新的问题，通常把这一问题称为前一个问题的一个“逆向”问题［2］，这也是解决这类“一题多问”的钥匙。

例2 设四边形ABCD为平行四边形，若边长AB=4，且向量AD的模为2。

⑴若平行四边形ABCD对角线交点为E，求E的轨迹方程。

⑵若一椭圆的焦点为A、B，过点A作直线交椭圆于P、Q两点，且∣PQ∣=，PQ的中点到Y轴的距离为，求这个椭圆的方程。

解:(1)本题的向量因子是CD的模为2，需要建立坐标系将平行四边形的相关条件进行转移。以平行四边形的一条边AB为X轴，不妨以其中点为原点，建立如图2所示的坐标系，就构造出向量、，依题意可设P、D两点的坐标是(x，y)、(x0，y0).

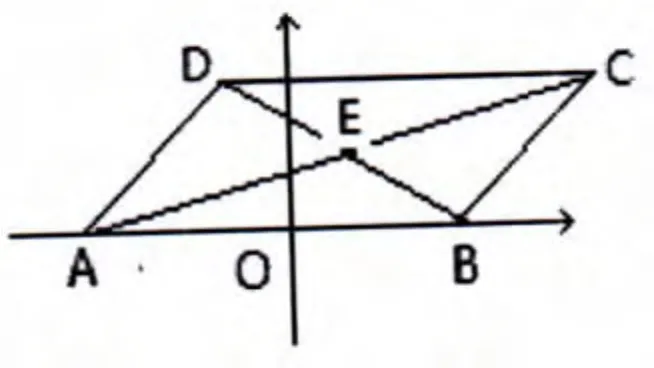
图2

依向量的运算可得:向量(4，0)与向量(x0+2，y0)的和等于 2(x+2，y)，于是有向量(x0+6，y0)和向量(2x+4，2y)产生，再进行向量计算可得

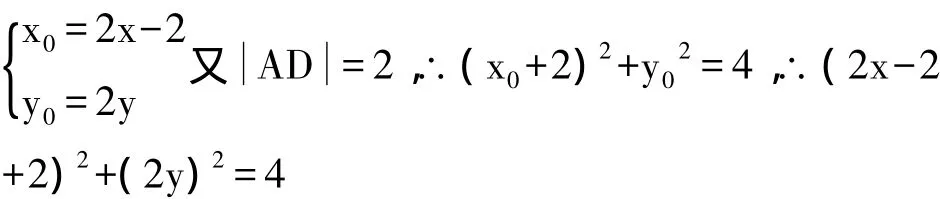
⑵将问题⑴这一结论转移成条件，作逆向问题再探即可。设过A的直线方程为y=k(x+2)

以A、B为焦点的椭圆的焦距为4，则有C=2于是可设椭圆方程为:

依此容易求得b2=4，∴所求椭圆方程为

3 交汇类问题

问题解析:这类问题，属于较为复杂的动点轨迹问题，其已知点是动点，轨迹点也是动点(尤其是本题中轨迹点为两条动曲线交点)，可以先设定参数并构造向量，求解时可以先将向量因子转化为几何条件进而换算成代数式，再利用“交轨法”以求出二动曲线的方程或适合动点坐标的含参关联等式，然后进行消参即可。

例3 设有抛物线为y2=2px如图3，若OA、OB是过该抛物线顶点O的两条弦，且=0，现有以OA、OB为直径的两个动圆，求这两个动圆的另一个交点P的轨迹。

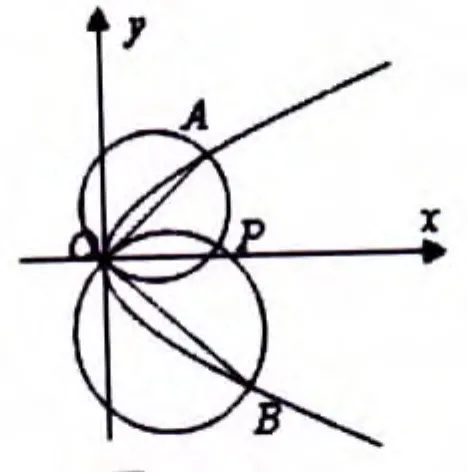
图3

解:先构造向量OA，借以活化题设中的点积条件，设定参数k后就有了解题的路经，最后进行消参就可以了。所以:

设直线OA的斜率为k，显然k存在且不等于0，则OA的方程为y=kx

解这个方程组得点B的坐标为(2pk2，－2pk)于是有:两条弦OA、OB的中点分别为M(，)和N(pk2，－pk)以此为条件再建立分别以OA、OB为直径的圆的含参数k方程，分别为:

∵P(x，y)是不同于原点的两个圆的另外一个交点，所以 x≠0，y≠0

由③和④消去k，就可以得方程:x2+y2－2px=0.由上可知，所求动点P的运动轨迹是为以p为半径，以点(p，0)为圆心的一个(不含原点的)圆。

总之，根据已知条件求方程这类问题，若已知条件中隐匿着向量因子(或幅、模、角，或点、叉积等)，从数学的角度来说，它可以整合空间形式与数量关系而形成知识网的交汇结点，以交叉互通的形式承载向量、方程、曲线、函数、不等式等多项数学知识和运算而成为解析几何的明珠;从老师的教学的角度来看，它不仅可以沟通代数、几何与三角的内在联系，来展示数学的奥妙，还能把代数的准确描述与几何图形的直观刻画耦合起来，去发展学生的创造性思维;从学生的学习来看，它“以数隐形，以形示数，数形互渗”，以其动态性和不确定性会给学生的学习造成困难。由于此类问题的求解，所涉及的知识点较多，内涵丰富，对考生的思维品质和变通能力的要求也较高;因此，多年来一直是高考的必备题型，其求解规律值得同行深究。

［1］朱赛飞.向量欣赏［J］.数学教学，2010(06):封二.

［2］谢之生等.平面向量的实数化模型［J］.数学通讯，2003(05):16～18.