基于时-空稀疏解的方位超分辨算法∗

杨广玉,马晓静,杨雪亚

(1.中国电子科技集团公司第三十八研究所，安徽合肥230088;2.电子工程学院，安徽合肥230037)

0 引言

对于同一距离单元或者邻近距离单元内的多个目标，对回波数据进行脉冲压缩无法从距离上进行分离，由于雷达相干脉冲数通常较少，也无法从多普勒维对径向速度接近的目标进行分离，这里考虑从方位角进行测量分辨多个目标。现有的方位角测量方法基本上是基于和、差波束或者多波束比幅的经典单脉冲测角方法。但是，在同一接收波束内存在多个目标时，单脉冲测角方法无法区分多个目标，导致误差变大、甚至完全失效。

实际上，改善方位角测量性能的关键是提高方位分辨率，因此，需要采用阵列超分辨技术对方位角进行估计。阵列超分辨算法以多重信号分类算法(MUSIC[1-2])及最大似然[3-4]算法(ML)为代表。MUSIC算法对信噪比和快拍数要求较高，而且对相关目标回波信号需要进行空间平滑，造成阵列孔径的损失。ML等参数化方法是一种渐近无偏估计，然而这类方法通常需要全局极值的多维搜索，多目标时无法满足实时处理。文献[5]采用基于去卷积的方法得到目标空间位置分布函数，不过去卷积方法对逆滤波器的参数选择、扫描波束等比较敏感，同时对信噪比有较高的要求。

稀疏分析在一组基向量中通过某种变换关系对应于信号的某个稀疏向量来表示信号的特征。文献[6]研究了基于l1范数的基向量选择问题，Rao[7-8]将其拓展至形式更为普遍的l(p≤1)稀疏度量，提出了FOCUSS(FOCal Underdetermined System Solver)算法，Cotter[9]将稀疏分析应用于多向量的情况下，综合利用多个快拍，便于实际应用。Malioutov[10]将其应用于均匀线阵的角度估计问题中，并提出了一种基于接收数据奇异值分解的简化算法。文献[11]将稀疏解应用于米波雷达测高问题中，改善了仰角分辨率和测高精度。

本文综合利用回波中包含的多普勒信息和空域信息，建立了基于时-空l(p≤1)类范数的稀疏度和2范数约束的数学模型，依次沿时域快拍和空域阵元求稀疏解，等效地拓展了快拍数长度和阵列孔径，显著提高了角度分辨率，从而实现对多个目标的分辨和方位角估计。

1 信号模型

针对阵元间距为d、水平放置的N个阵元组成的均匀线阵(ULA)，多普勒频率为f k的K个远场窄带目标的回波信号分别以方位角θk，k=1，2，…，K入射到阵列。

以N×L的矩阵X表示阵列接收的L个快拍的数据，则有

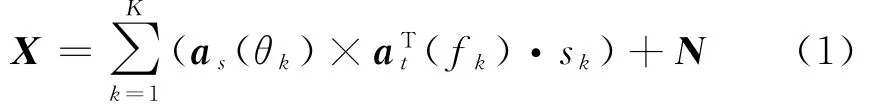
式中，

a s(θk)=[1 exp(j2πd/λsin(θk)) … exp(j2π(N-1)d/λsin(θk))]T为阵列对第k个目标的导向矢量;s k为第k个目标回波信号的复包络;a t(f k)=[0 exp(j2πf k Tr) … exp(j2πf k(L-1)Tr)]T为L个回波周期对第k个目标多普勒频率f k的导频矢量，Tr为采样间隔是脉冲重复周期;N为与信号不相关的复高斯白噪声矩阵。则数据矩阵X的结构如图1所示。

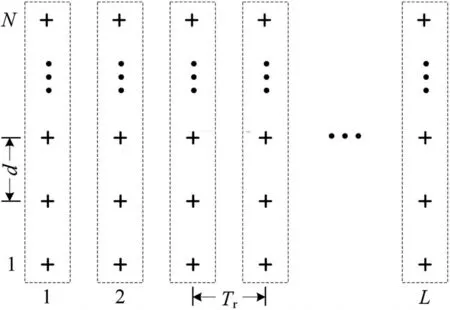
图1 时-空回波数据结构

2 多普勒频率角度估计

2.1 稀疏解

对于式(1)所示的N×L的信号矩阵X，求沿X的列方向的稀疏解，即是求解满足如下线性方程组的Y:

式中，F为一个N×M的行满秩矩阵，Y为一个M×L的稀疏矩阵，即其每一列的大部分元素均为0，M≫N以保证矩阵的稀疏性，噪声矩阵V的每个元素均为独立同分布的高斯变量，其方差为σ2。

假设Y的每个元素是服从广义高斯分布的变量，其广义方差为β。Y的最大后验估计是通过最小化式(3)所示的函数得到的[8]:

式 中，‖·‖F表示Frobenius范数为稀疏度量，，参数p(0＜p≤1)控制Y的概率密度分布的形状。由E(p)(Y)的表达式可见，Y的列元素是通过l(p≤1)范数结合的，产生了稀疏效果[10]，而行元素是由2范数结合的，没有稀疏效果，综合利用了L个快拍数据。

对J(Y)求导并令其等于0，得到求稀疏解Y[9]的迭代过程为

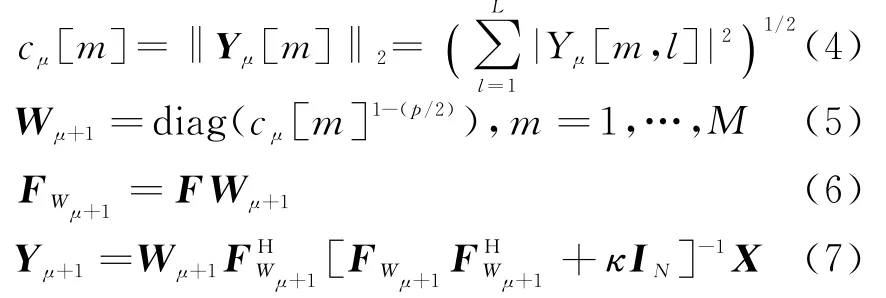
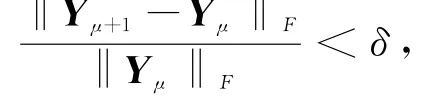
2.2 基于稀疏解的多普勒-角度估计

这里将以上稀疏解应用于多普勒频率和角度估计问题中，求回波数据X的两维稀疏解。稀疏解进行超分辨的原理是进行时-空二维稀疏拓展，从多普勒和角度两维信息对目标进行分辨。如图2所示，对接收数据X进行常规处理无法分辨多个目标，首先求一维时间稀疏解YT，等效地将快拍数从L拓展到L t，提高了多普勒维的分辨率;然后求二维时-空稀疏解Z，等效地将阵元数从N拓展到N s，提高了角度分辨率。

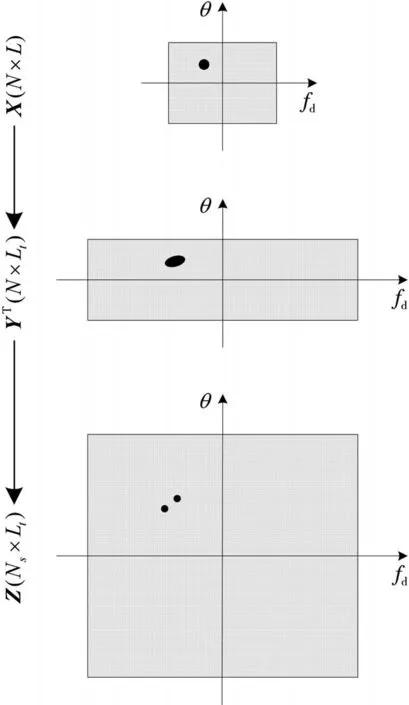
图2 时-空二维稀疏解示意图

由迭代算法求阵列的接收数据X沿时间维的稀疏解矩阵Y，等效地将每个阵元接收信号的长度从L拓展到L t，而沿阵列方向没有稀疏效果。算法描述为

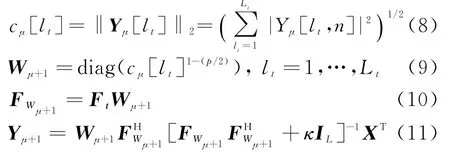
式中，F t为一个L×L t的DFT系数矩阵[12]，其元素F t[l，l t]=(1/L t)ex p(j2πll t/L t)。 迭 代 结束后得到的L t×N的稀疏矩阵Y对应于X在范数约束下沿行方向拓展矩阵的DFT。当f k Tr=l tk/L t，k=1，…，K时，|Y(n)|会在l tk位置出现K个峰值与K个信号频率对应，其中Y(n)表示Y的第n列。

类似地，沿列稀疏矩阵YT的阵列方向进行稀疏变换，得到N s×L t的二维稀疏矩阵Z。过程描述如下:

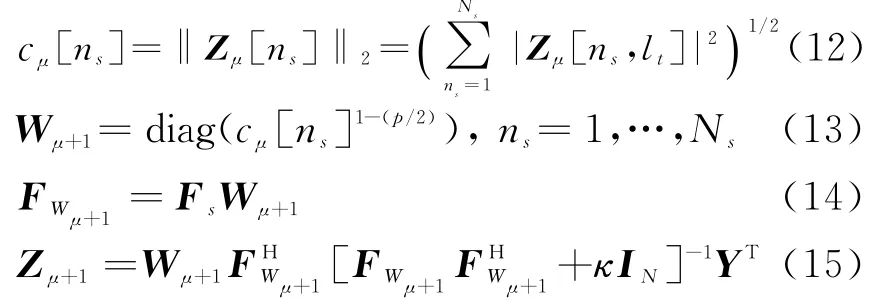
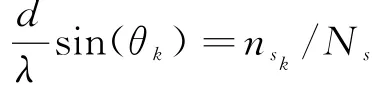
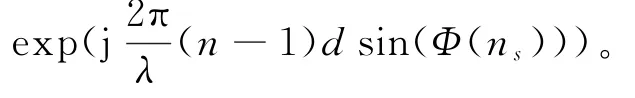
3 仿真分析

为了验证稀疏解方法对方位超分辨估计的有效性，给出计算机仿真结果。仿真所使用的阵列是20个阵元组成的ULA，阵元间距半波长。取δ=0.01。

假设两个目标距离均为200 km、方位角分别为θ1=-1.1°和θ2=1.1°，径向多普勒频率分别为160 Hz和176 Hz，此时两个目标回波信号部分相关，单元信噪比5 dB，回波快拍数10。稀疏解的长度L t=256，N s=512，p=0.2。经过16次迭代，一维时间稀疏解收敛，迭代过程的稀疏解的幅度变化如图3(a)所示，在迭代过程中逐渐增强信号分量、压低噪声功率，稀疏解在真实多普勒频率附近形成两个尖锐的峰值，最终多普勒频率的估计值分别为161.8 Hz和179.4 Hz;图3(b)为二维稀疏解幅度的投影图，两个极大值对应的方位角分别为-1.12°和1.12°。

图3 部分相关信号的稀疏解

设多普勒频率均为160 Hz的两个相干目标，其他条件和上面仿真一致，并和空间平滑MUSIC(SS-MUSIC)的空间谱进行比较。由于两个目标的多普勒频率相同，因此一维时间稀疏解的峰值只有一个，如图4(a)所示，多普勒估计值为161.8 Hz;图4(b)为时-空二维稀疏解的归一化幅度，在相应的目标参数处，二维稀疏解出现两个尖锐的峰值;图4(c)给出了二维稀疏解俯仰角剖面图和相同条件下的空间平滑MUSIC(SS-MUSIC)的空间谱，可见，受低信噪比和信号相干性的影响，MUSIC空间谱无法分辨角度间隔很小的两个目标，而时-空二维稀疏解具有更高的角度分辨率，在目标真实仰角附近形成两个峰值。

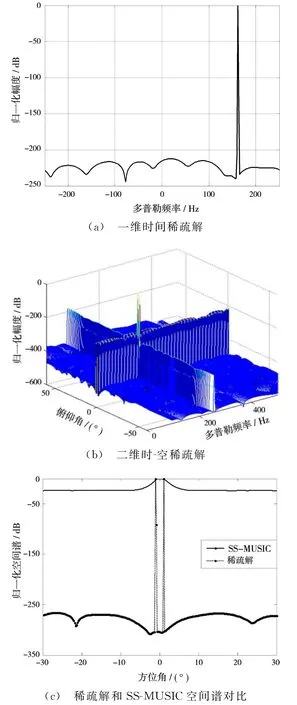
图4 相干信号的稀疏解

以上仿真结果充分表明了稀疏解方法在多普勒频率方位角时-空二维分辨的有效性，其高分辨率、低噪声门限和超低副瓣特性是传统超分辨算法无法达到的。

4 结束语

对于从距离和多普勒频率无法分辨的目标，可以考虑使用阵列超分辨技术，从方位角实现多个目标的分离。受限于信噪比、快拍数和目标相干性等因素，常规超分辨算法对方位角的分辨和测量效果不理想。为此提出了一种具有高分辨率和高测量精度的时-空二维稀疏解的方位超分辨方法，通过迭代法依次沿快拍维和阵元维求稀疏解，利用多普勒和角度两维信息对目标进行分辨。由于利用了多普勒信息，该方法改善了方位角分辨性能，同时对目标的相干性不敏感，可用于相干条件下方位超分辨。仿真结果表明了其相对于传统超分辨算法的良好测高性能。

[1]KUNDU D.Modified MUSIC Algorithm for Estimating DOA of Signals[J].IEEE Trans on Signal Processing，1996，48(1):85-90.

[2]THAKRE A，HAARDT M，GIRIDHAR K.Single Snapshot Spatial Smoothing with Improved Effective Array Aperture[J].IEEE Signal Processing Letters，2009，16(6):505-508.

[3]STOICA P，SHARMAN K.Maximum Likelihood Methods for Direction-of-Arrival Estimation[J].IEEE Trans on Acoustics，Speech，and Signal Processing，1990，38(7):1132-1143.

[4]TADAION A A，DERAKHTIAN M，GAZOR S，et al.A Fast Multiple-Source Detection and Localization Array Signal Processing Algorithm Using the Spatial Filtering and ML Approach[J].IEEE Trans on Signal Processing，2007，55(5):1815-1827.

[5]盛卫星，方大纲，杨正龙，等.一般非综合孔径雷达方位超分辨研究[J].南京理工大学学报，2000，24(4):289-295.

[6]ROMBERG J K.Sparse Signal Recovery vial1Minimization[C]∥2006 40thAnnual Conference on Information Sciences and Systems，Princeton，NJ:[s.n.]，2006:213-215.

[7]RAO B D，KREUTZ-DELGADO K.An Affine Scaling Methodology for Best Basis Selection[J].IEEE Trans on Signal Processing，1999，47(1):187-200.

[8]RAO B D，ENGAN K，COTTER S F，et al.Subset Selection in Noise Based on Diversity Measure Minimization[J].IEEE Trans on Signal Processing，2003，51(3):760-770.

[9]COTTER S F，RAO B D，ENGAN K，et al.Sparse Solutions to Linear Inverse Problems with Multiple Measurement Vectors[J].IEEE Trans on Signal Processing，2005，53(7):2477-2488.

[10]MALIOUTOV D，CETIN M，WILLSKY A S.A Sparse Signal Reconstruction Perspective for Source Localization with Sensor Arrays[J].IEEE Trans on Signal Processing，2005，53(8):3010-3022.

[11]杨雪亚，杨广玉.基于稀疏解的米波雷达测高方法[J].雷达科学与技术，2012，10(6):629-632.

[12]SACCHI M D，ULRYCH T J，WALKER C J.Interpolation an Extrapolation Using a High-Resolution Discrete Fourier Transform[J].IEEE Trans on Signal Processing，1998，46(1):31-38.