二次预应力外包钢组合梁叠合楼盖动力特性有限元分析

吴 庆，李 俊，张道明

(1.江苏科技大学土木工程与建筑学院，江苏镇江，212003)

(2.齐齐哈尔大学建筑与土木工程学院，黑龙江齐齐哈尔，161006)

近年来，组合楼盖体系在高层建筑结构中已得到越来越广泛的应用［1］.在组合楼盖体系中，组合梁通常仅作为竖向承重构件使用［2］.二次预应力外包钢组合梁叠合楼盖是通过焊接并施加预应力，使预制外包钢梁形成纵横交叉梁体系，张拉预应力后，在钢槽内填充轻骨料混凝土，并在该交叉梁结构体系上现浇混凝土叠合楼盖混凝土板，待混凝土达到设计强度和交叉梁体系形成肋梁结构，再次施加预应力，使组合结构形成预应力整体组合结构，共同承担楼盖荷载.因此，该交叉梁结构应具有足够的强度和刚度，满足叠合楼盖施工过程荷载对其承载性能的要求.该叠合楼盖施工分两阶段:第一阶段是预制外包钢组合梁组合形成交叉梁体系，并施加预应力改善该组合式交叉梁结构体系的力学性能，成为后续现浇叠合楼盖板施工的支撑结构体系;第二阶段待现浇叠合楼盖混凝土达到设计强度，再次张拉预应力改善组合楼盖体系整体承载性能.

叠合楼盖施工过程如下:①制作外包钢钢槽(图1).②在钢槽内通过钢筋设置预应力筋位置控制点和建立连接件(在外包钢内焊接钢板或钢筋)，防止混凝土与钢板滑移(图2)［3］.③在钢槽内铺设底部预应力筋和上部预应力筋孔道.④张拉底部的预应力筋，在钢槽内浇筑轻骨料混凝土.⑤在柱上焊接安装外包钢组合梁，将预应力筋锚固在柱子外侧，底部预应力筋和组合梁共同承担荷载.⑥支叠合楼盖模板和安装楼盖板钢筋，浇筑混凝土.⑦待楼盖板混凝土达到设计强度张拉上部预应力筋，锚固在柱子侧面形成交叉梁组合式叠合楼盖整体结构，共同承担自重和外荷载(图3).

图1 预应力筋位置Fig.1 Position of prestressing tendon

图2 预应力组合梁Fig.2 Built-up beam of prestressing tendon

图3 预应力组合梁Fig.3 Built-up beam of prestressing tendon

对于叠合楼盖安装阶段，由于施工中振动设备的存在，为了不发生共振，需要使结构的自振频率远大于或远小于振动设备所产生的振动频率［4］.所以对于叠合楼盖安装阶段自振频率的研究是有必要的.本文通过有限元方法对该叠合楼盖动力性能进行分析，并通过调整预应力大小、预应力布筋形态和柱的约束条件等进行参数分析，为叠合楼盖体系抗震性能的研究提供基础.

1 结构动力分析类型

模态分析是用来确定结构振动特性的一种技术，主要用于确定结构的固有频率、振型及振型参与系数等，而固有频率和振型的确定是承受动态荷载结构设计中的重要参数，也是其他各类动力学分析的基础.此外，模态分析可以使结构设计避免共振或以特定的频率进行振动，可以进一步深入了解结构对于不同类型的动力荷载的响应情况，并有助于在其他动力分析中估算求解控制参数，因此大多数结构要进行模态分析［5］.

ANSYS中的模态分析属于线性分析，对于结构的一些非线性特性，如塑性及接触单元等非线性问题，ANSYS不作考虑.ANSYS中针对不同的情况，常用的模态分析方法主要有Subspace法、Block Lanczos法、Power Dynamics法、Reduced法、Unsymmetric法及Damped法.根据二次预应力外包钢组合梁叠合楼盖的特点，本文选用Block Lanczos法进行结构的模态分析［6］.

2 有限元模型的建立

2.1 研究对象

通过有限元软件ANSYS建立了二次预应力外包钢组合梁叠合楼盖模型并对动力性能进行了模拟分析.整体楼盖共14.4m×18m，中间梁采用二次预应力外包钢组合梁，中间梁与外环梁截面尺寸均为300mm×800mm，外包钢板上翼缘板尺寸为100mm×5mm，腹板厚度为5mm，底板厚度为10 mm.梁与柱刚接，柱子总长度为8m，两端铰接.预应力筋分别采用二次抛物线形及折线形，其结构平面及预应力筋布置情况如图4所示.

图4 结构平面及预应力筋布置Fig.4 Structure plan and layout of tendons

安装阶段U型外包钢梁1和2二次抛物线形预应力筋方程为:

U型外包钢梁3和4二次抛物线形预应力筋方程为:

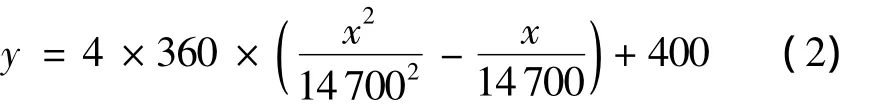
使用阶段U型外包钢梁1和2二次抛物线形预应力筋方程为:

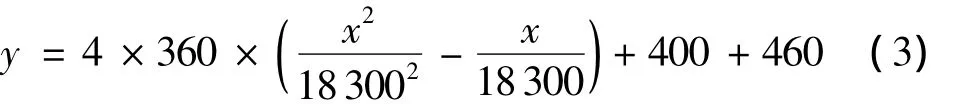
U型外包钢梁3和4二次抛物线形预应力筋方程为:

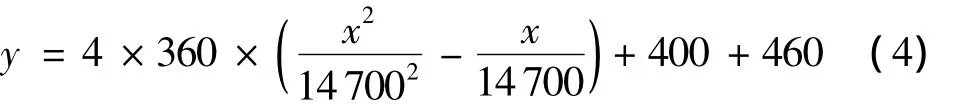
安装阶段U型外包钢梁1和2折线形预应力筋方程为:

U型外包钢梁3和4折线形预应力筋方程为:

使用阶段U型外包钢梁1和2折线形预应力筋方程为:

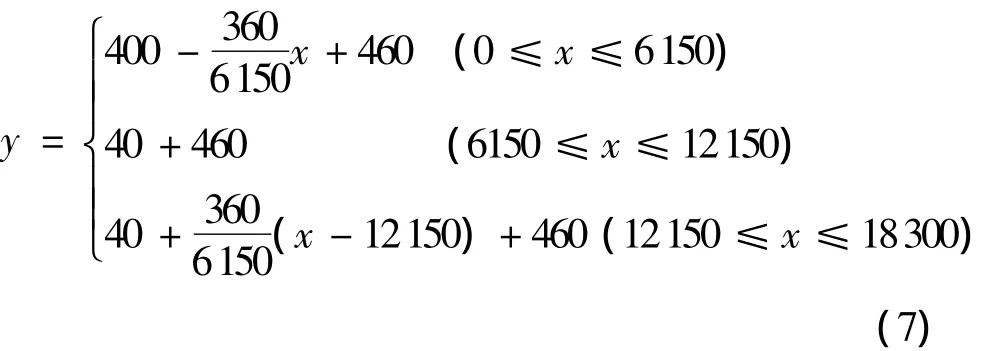
U型外包钢梁3和4折线形预应力筋方程为:

安装阶段预应力筋束截面面积为2 200mm2，使用阶段预应力筋束截面面积为800mm2，弹性模量为1.95×105MPa.柱截面尺寸为500mm×500 mm，现浇叠合楼板板厚为120 mm，受拉区配置10@100钢筋网，保护层厚度40mm.采用LC25轻骨料混凝土，密度标准值1 650 kg/m3，轴心抗压强度fc=12.5MPa，抗拉强度ft=1.30MPa，弹性模量E=14.2×103MPa，泊松比为0.2.楼板钢筋采用HRB335，外包钢板采用Q400钢材.楼盖模板体系自重为0.35 kN/m2，施工荷载(施工器具，人员自重1 kN/m2以及振捣混凝土时产生的荷载为2 kN/m2)，使用阶段楼面活荷载为3 kN/m2.

2.2 单元选用及界面处理

在有限元模型中采用SOLID65模拟混凝土的受力，楼板混凝土配筋在建模中采用整体式钢筋模型.采用BEAM4模拟柱，LINK8模拟普通钢筋和预应力筋.

采用SHELL181模拟外包刚板，该单元适合对薄的壳体结构数值分析，是一个4结点单元，每个结点具有6个自由度:x，y，z方向的位移自由度和绕X，Y，Z轴的转动自由度.SHELL181单元非常适用于分析线性的大转动变形和非线性的大形变，通过几何常数模块，可控制壳体厚度的变化.

考虑到外包钢板与混凝土之间无滑移，二者变形协调，所以在建模过程中界面采用了共用节点，不考虑钢板与混凝土界面相对滑移.

2.3 材料本构关系

计算中混凝土的单轴受压应力－应变关系及钢材的单轴本构关系均采用线性本构关系.

2.4 边界条件及荷载施加

对柱施加铰接约束，安装阶段施加第1批预应力、自重及施工荷载;使用阶段施加第2批预应力，楼面施加均布活荷载向下，单元划分及有限元模型如图5所示.

图5 安装阶段及使用阶段有限元模型Fig.5 Finite elementmodel of the installation and using phase

3 有限元计算结果

3.1 结构振动特性结果分析

采用抛物线形布筋方式，安装及使用阶段预应力按两阶段张拉控制力分别施加.

安装阶段U型外包钢梁1和2上预应力筋有效张拉控制力为2314.4 kN.

安装阶段U型外包钢梁3和4上预应力筋有效张拉控制力为1125.8 kN.

使用阶段U型外包钢梁1和2上预应力筋有效张拉控制力为1012.5 kN.

使用阶段U型外包钢梁3和4上预应力筋有效张拉控制力为455.2 kN.

对新型楼盖体系的模态进行了有限元分析，并提取了前6阶的频率和振型.

图6 安装阶段结构前6阶振型Fig.6 First six modes of the installation phase

①安装阶段前6阶的频率和振型见表1和图6.由表1和图6可知，安装阶段第1，2，3阶振型对应的频率较接近，第4，5阶振型的频率较接近.前6阶振型中的频率分布主要集中在3个区域:第1～3振型，第4～5振型，第6振型.

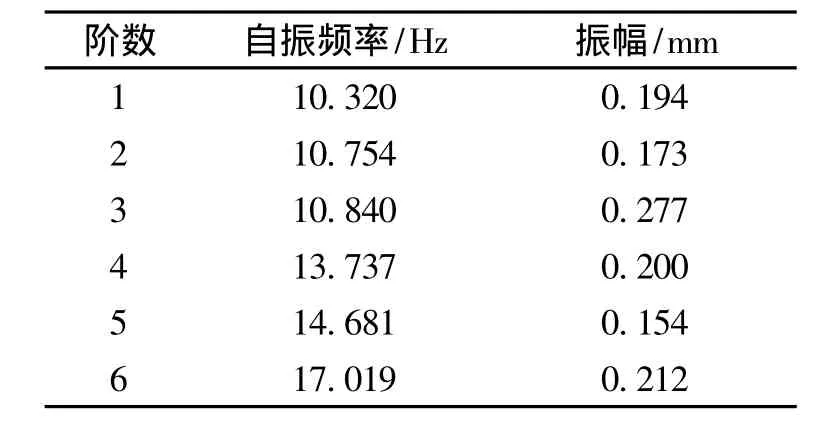
表1 安装阶段结构前6阶的自振频率及振幅Table1 First six natural frequencies and amp litudes of installation phase

②使用阶段前6阶的频率和振型见表2和图7.

表2 使用阶段结构前6阶的自振频率及振幅Table2 First six natural frequencies and amplitudes of using phase

图7 使用阶段结构前6阶振型Fig.7 First six modes of the using phase

由表2和图7可知，使用阶段第1，2阶振型对应的频率较接近，第3，4阶振型的频率较接近，第5，6阶振型的频率较接近.前6阶振型中的频率分布主要集中在3个区域:第1～2阶振型，第3～4阶振型，第5～6阶振型.

对比表1和表2可知，使用阶段的自振频率明显低于施工阶段的自振频率，这是由于使用阶段楼板的浇筑使得结构的质量大幅增加，从而结构使用阶段自振频率明显减小.同时使用阶段的振幅也明显低于施工阶段，这是由于第2批预应力的施加对结构的变形起到一定的约束作用，同时预应力的施加也提高了结构的刚度，因此结构的振幅明显降低.

对于频率标准，早期我国规范《高层民用建筑钢结构技术规程》(JGJ99－98)对钢－混凝土组合楼板振动舒适度采用频率限制，自振频率应控制在15Hz以上［7］.对于《规程》中对于15 Hz要求的限制，文献［8］中通过计算和试验研究指出该要求过于严格，高于加拿大国家规范5Hz以及欧洲规范9 Hz，无法合理指导工程设计，并建议参考外国相关规定与实测分析，将一般工程的组合楼板自振频率控制在9 Hz即可满足使用要求.从这种意义上来说，二次预应力外包钢组合梁叠合楼盖的自振频率基本能够满足正常使用的要求.

3.2 结构动力特性参数分析

3.2.1 预应力大小

同样的结构在不同的应力状态下，其动力特性也会不同，施加预应力对结构的自振频率会产生影响.因此，为了准确的对结构进行设计和动力分析，必须要对无预应力和有预应力两种情况进行模态分析［9］.当结构承受的外荷载很大，则所需施加的预应力也很大时，必须考虑对大幅增加预应力的情况进行模态分析.二次预应力外包钢组合梁叠合楼盖的模态分析与非预应力外包钢组合梁叠合楼盖模态分析基本方法和需要考虑的事项基本相同，但预应力模态分析需要先作施加预应力时结构的静力分析，然后作有预应力的模态分析，并且打开预应力分析开关［10］.本次分析以抛物线形预应力筋，柱端采用铰接的结构为例，分析预应力的大小对结构模态的影响，并分析其对结构动力特性的影响.

分别对预应力筋施加的预应力大小为0，Np，10Np(Np为有效预应力张拉控制力)的情况进行了模态分析，并提取了前6阶的振型、频率和振幅.不同预应力大小下结构体系前6阶自振频率f及振幅A的比较见图8～11，n为阶数.

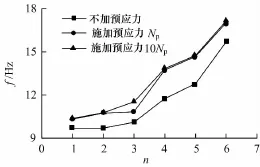
图8 安装阶段不同预应力下的自振频率Fig.8 Natural vibration frequencies of the installation phase in condition of different prestressing force

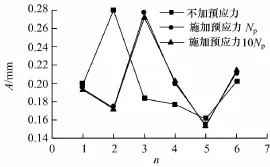
图9 安装阶段不同预应力下的振幅Fig.9 Vibration m ode of the installation phase in condition of different prestressing force

图10 使用阶段不同预应力下的自振频率Fig.1 0 Natural vibration frequencies of the using phase in condition of different prestressing force

图11 使用阶段不同预应力下的振幅Fig.1 1 Vibration mode of the using phase in condition of different prestressing force

由图8～11可知，安装阶段施加预应力后结构的频率明显升高.这是由于施加预应力对结构的变形起到了一定的约束作用，此外也增加了结构的刚度，因此使结构的自振频率升高.但施加的预应力从Np增大到10Np时结构振型、频率和振幅的变化不大，说明预应力的增大对结构的频率和振幅影响不大.使用阶段施加预应力后结构自振频率和振幅略有增大，施加的预应力从Np增大到10Np时结构的自振频率和振幅变化不大，说明预应力的变化对使用阶段结构刚度的影响很小.

3.2.2 预应力筋布筋形态

在预应力大小相等，柱约束条件相同的条件下，仅改变预应力筋的布筋形态，分别对结构布置抛物线、折线预应力筋的情况进行了模态分析并提取了前6阶的振型、频率和振幅.不同布筋形态下结构体系前6阶自振频率及振幅的比较见图12～15.

由图12～15可知，改变预应力筋布筋形态后，结构自振频率和振幅都发生微小变化，但变化趋势相同.这是由于布筋形态的改变使得结构的质量和刚度出现微小变化所致.

图12 安装阶段不同预应力筋线型的自振频率Fig.1 2 Natural vibration frequencies of the installation phase in condition of different layout of tendons

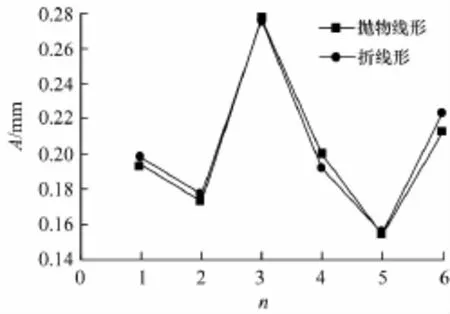
图13 安装阶段不同预应力筋线型的振幅Fig.1 3 Vibration mode of the installation phase in condition of different layout of tendons

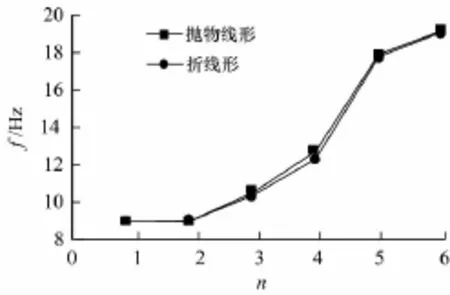
图14 使用阶段不同预应力筋线型的自振频率Fig.1 4 Natural vibration frequencies of the using phase in condition of different layout of tendons

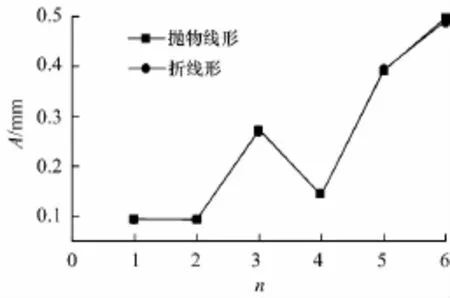
图15 使用阶段不同预应力筋线型的振幅Fig.1 5 Vibration mode of the using phase in condition of layout of tendons

3.2.3 柱的约束条件

由于柱约束条件会影响结构的刚度，从而影响结构的动力特性，因此，对柱约束为刚接和铰接两种情况分别建模，分析其对振动频率和振幅的影响.

在预应力大小相等，预应力筋布筋形态相同的条件下，仅改变柱的约束条件，分别对柱施加铰接和刚接约束的情况进行了模态分析并提取了前6阶的振型、频率和振幅.不同约束条件下结构体系前6阶自振频率及振幅的比较见图16～19.

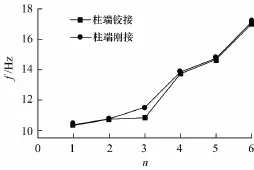
图16 安装阶段不同约束下的自振频率Fig.1 6 Natural vibration frequencies of the installation phase in condition of different constrained condition of column

图17 安装阶段不同约束下的振幅Fig.1 7 Vibration mode of the installation phase in condition of different constrained condition of column

图18 使用阶段不同约束下的自振频率Fig.1 8 Natural vibration frequencies of the using phase in condition of different constrained condition of column

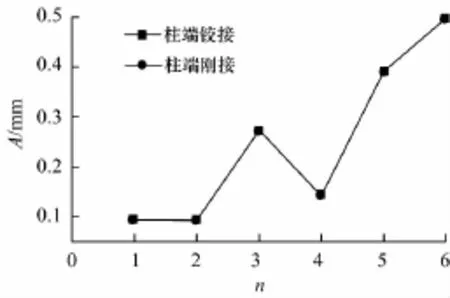
图19 使用阶段不同约束下的振幅Fig.1 9 Vibration mode of the using phase in condition of constrained condition of column

由图16～19可知，安装阶段结构铰接模型对应的频率均低于刚接模型对应的频率，说明柱约束条件的减弱使得整个结构的刚度减小，从而使结构的自振频率降低，振幅也略有减小.使用阶段结构铰接模型对应的频率和振幅与刚接模型对应的频率和振幅相同，说明柱约束条件的变化对使用阶段结构刚度的影响很小.

4 结论

1 )二次预应力外包钢组合梁叠合楼盖的自振频率基本能够满足正常使用的要求.

2 )预应力的施加使安装阶段结构的频率明显升高，增大预应力对安装阶段结构频率和振幅影响不大;预应力的施加和增大对于使用阶段结构的频率和振幅影响均很小.

3 )预应力筋布筋形态的不同使结构自振频率和振幅都发生微小变化，但变化趋势相同.

4 )柱约束条件的变化使安装阶段结构的自振频率和振幅都发生变化，但对使用阶段结构的自振频率和振幅的影响很小.

References)

［1］ 聂建国，余志武.钢－混凝土组合梁结构在我国的研究及应用［J］.土木工程学报，1999，32(2):3－8.

Nie Jianguo，Yu Zhiwu.Research and practice of composite steel-concrete beams in China［J］.China Civil Engineering Journal，1999，32(2):3－8.(in Chinese)

［2］ 田春雨，聂建国.组和楼盖竖向承重体系中楼板变形及内力分析［J］.工程力学，2006，23(5):62－66.

Tian Chunyu，Nie Jianguo.Analysis of deflection and internal force in composite slab-on-girder floor system［J］.Engineering Mechanics，2006，23(5):62－66.(in Chinese)

［3］ 张道明.新型预应力外包钢组合梁抗弯性能的研究［D］.辽宁沈阳:东北大学，2007.

［4］ 周建明，陈阳.楼盖竖向自振频率简化计算与控制方法的研究［J］.力学季刊，2013，34(1):147－153.

Zhou Jianmin，Chen Yang.Research on simplified calculation method and control of floor's perpendicular basic frequency［J］.Chinese Quarterly of Mechanics，2013，34 (1):147－153.(in Chinese)

［5］ 邱继生，黄炜，侯俊峰.钢纤维混凝土密肋复合楼盖体系动力特性的有限元分析［J］.四川建筑科学研究，2013，39(1):14－17.

Qiu Jishen，Huang Wei，Hou Junfeng.Finite element analysis of dynamic characteristic of multi-rib composite slab structure system containing steel fiber［J］.Sichuan Building Science2013，39(1):14－17.(in Chinese)

［6］ 李皓月，周田鹏，刘相新.ANSYS工程计算应用教程［M］.北京:中国铁道出版社，2003.

［7］ 中华人民共和国建设部.JGJ(99－98)高层民用建筑钢结构技术规程［S］.北京:中国建筑工业出版社，1998.

［8］ 何文汇，马智刚.组合楼板自振频率的计算与试验研究［J］.钢结构，2005，20(3):57－59.

He Wenhui，Ma Zhigang.Experimental studies and calculation of natural vibration frequency of composite floors［J］.Steel Construction，2005，20(3):57－59.(in Chinese)

［9］ 张耀庭，汪霞利，李瑞鸽.预应力梁固有频率的试验研究［J］.华中科技大学:自然科学版，2007，35(2):12－15.

Zhang Yaoting，Wang Xiali，Li Ruige.Experimental research on nature frequency of prestressed concrete beams［J］.Huazhong University of Science and Technology: Natural Science Edition 2007，35(2):12－15.(in Chinese)

［10］ 王新敏.ANSYS工程结构数值分析［M］.北京:人民交通出版社，2010.