二阶Camassa-Holm方程行波解的稳定性及性质

安 荣，丁丹平

(江苏大学理学院，江苏镇江212013)

2003年，Adrian Constantin和Boris Kolev在进行单位圆微分同胚群上的测地流时，首先得到了高阶Camassa-Holm方程，具体形式如下:

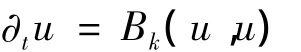
式中:k∈{0}∪N，∂tu=Bk(u，u):=ACk(u)-u∂x u，

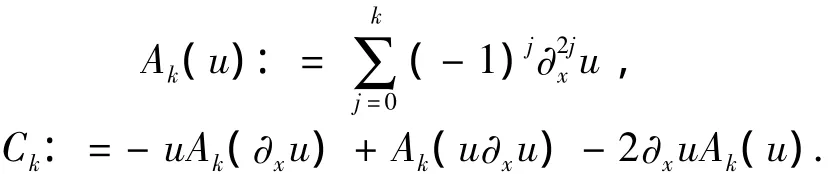
文献［1］研究了高阶Camassa-Holm方程的全局适定性.文献［2］研究了高阶Camassa-Holm方程Cauchy问题全局解的存在性.通过对局部频率方程采用小粘度方法确定了高阶Camassa-Holm方程有全局解，即若u0∈Hk(R)，且∀x∈R，u0(x)都为有限频段，即存在M＞0，使得P＞Mu0=0，则高阶CH方程有全局解:

u∈C(［0，∞);Hk-1(R1))∩L∞(［0，∞);Hk(R1))

并且全局解是能量守恒的.文献［3］中利用Kato定理证明了高阶Camassa-Holm方程和高阶双组份Camassa-Holm方程解的存在唯一性及连续性解的局部适定性定理，得到了方程的守恒量和解的先验估计，在此基础上得到解的整体存在性，另外还得到高阶双组份Camassa-Holm方程的爆破理论.当k=2时，高阶Camassa-Holm方程的具体形式如下:

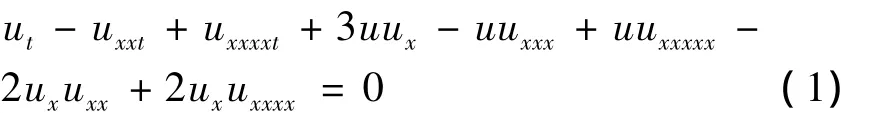
行波解为［4］

式中:c1c2=0.文献［5］中对著名的非线性哈密顿系统

进行理论的总结，提出了孤立波轨道稳定性理论.文献［6］中研究了CH方程孤立尖波解的稳定性问题，利用它的两个守恒量，证明了孤立尖波在H1范数意义下是轨道稳定的，受此启发，文中研究了方程(1)的行波解在H2范数意义下的稳定性;并对行波解在某一个时刻的零点分布研究，得到了行波解的零值分布.

1 行波解的稳定性

定理1［7－14］:若v∈(［0，T);H2(R))是方程(1)的一个解，如果有‖v(0，·)-φ‖H2＜δ，δ＞0，则有‖v(t，·)-φ(·-ct)‖H2＜ε.

注:在初始时刻接近行波的解，在它的存在时间内，必然与该行波的某个平移充分接近.

v(x，t)是方程(1)的一个解，φ(x，t)是方程(1)的行波解.记:v-φ=w，则

将式(3)代入方程(1)可得:

因为φ(x，t)是方程(1)的行波解，则

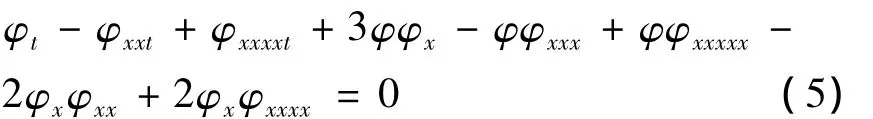
由式(4，5)可得

用w对式(6)在R上做内积，得到:

根据Holder不等式、施瓦茨不等式、Young不等式对下面的式子进行范数估计，得到:

由式(7，8)得到:

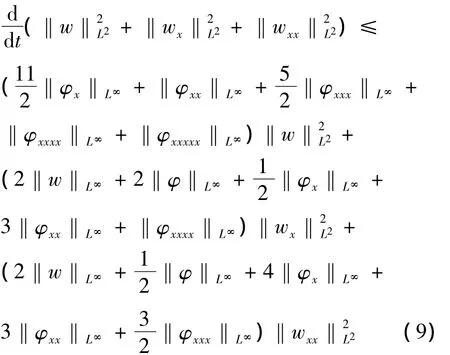
对‖φ‖L∞，‖φx‖L∞，‖φxx‖L∞，‖φxxx‖L∞，‖φxxxx‖L∞，‖φxxxxx‖L∞，‖w‖L∞做范数估计:

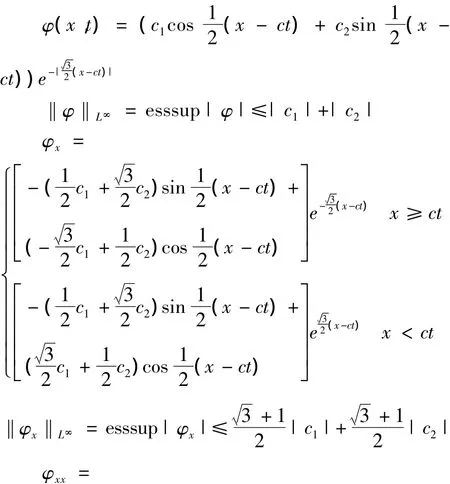
所以

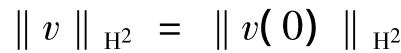
将L∞嵌入到H2中可得:

由式(9，10)得到:

由Grownwall不等式可得:

即:

可得:

即:

因此，称φ(x，t)是轨道稳定的.

2 二阶Camassa-Holm方程行波解的零值分布

当k=2时，高阶Camassa－Holm方程行波解:

式中:c为波速.

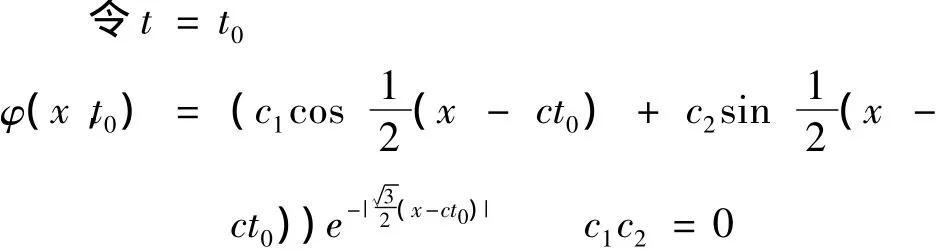
1 )当c1=0，c2≠0时，不妨设c2＞0，

(k为整数)，φ(x，t0)是递增的.

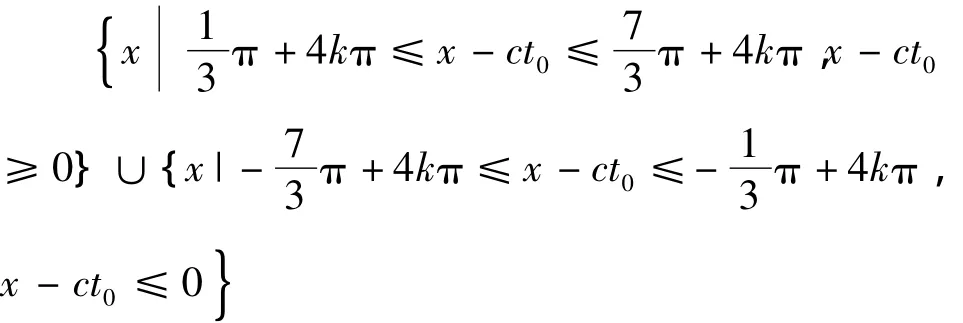
(k为整数)，φ(x，t0)是递减的.

则c1=0，c2＞0，x-ct0≥0时，

x=2nπ+ct0(n为自然数)是φ(x，t0)的零点.

c1=0，c2＞0，x-ct0＜0时，x=2nπ+ct0(n为整数)是φ(x，t0)的零点.

以x，φ(x，t0)建立直角坐标系，c1=0，c2＞0时，φ(x，t0)图像见图1.以上可以得到:

图1 c1=0，c2＞0时，φ(x，t0)Fig.1 Figure ofφ(x，t0)at c1=0，c2＞0

当c1=0，c2＞0时，φ(x，t0)的零点，极值点是相间的，从而得到行波解φ(x，t)的零值，极值是相间的.

2 )当c1≠0，c2=0时，不妨设c1＞0，

(k为整数)，φ(x，t0)是递增的.

(k为整数)，φ(x，t0)是递减的.

当c1＞0，c2=0，且x-ct0≥0时，

φ(x，t0)=0时，x=(2k+1)π+ct0(k为自然数)，则x=(2k+1)π+ct0是φ(x，t0)的零点.

c1＞0，c2=0，ε＜0时，

φ(x，t0)=0时，

x=(2k+1)π+ct0(k为整数)，则x=(2k+1)π+ct0是φ(x，t0)的零点.

以x，φ(x，t0)建立直角坐标系，c1＞0，c2=0时，φ(x，t0)图像见图2.

图2 c1＞0，c2=0时，φ(x，t0)Fig.2 Figure ofφ(x，t0)at c1＞0，c2=0

以上可以得到:

当c1＞0，c2=0时，φ(x，t0)零点、极值点是相间的，从而得到行波解φ(x，t)的零值、极值是相间的.

References)

［1］ Coclite GM，Holden H，Karlsen K H.Well-posedness of higher-order Camassa-Holm equation［J］.Journal of Differential Equations，2009，246(3):929－963.

［2］ Ding Danping，Lv Peng.Conservative solutions for higher-order Camassa-Holm equation［J］.Journal of Mathematical Physics，2010，51(7):86－92.

［3］ 张榀.一类高阶浅水波方程的适定性和爆破理论［D］.江苏镇江:江苏大学，2010:11－18.

［4］ 薛丰刚.高阶Camassa-Holm方程的行波解［D］.江苏镇江:江苏大学，2013:8－28.

［5］ Grillakis M，Statah J，Strauss W.Stability theory of solitary waves in the presence of symmetry［J］.Journal of Functional Analysis，1987，74(1):160－197.

［6］ Constantin A，Strauss W.Stability of peakon［J］.Commun Pure Appl Math，2000，53:603－610.

［7］ Constantin A，Escher J.Global existence and blow-up for a shallow water equation［J］.Annali della Scuola Normale Superiore di Pisa-Classe di Scienze，1988，26(2): 303－328.

［8］ Constantin A，Escher J.Globalweak solution for a shallow water equation［J］.Indiana Univ Math，998，47: 1527－1545.

［9］ Rodriguez-Blanco G.On the cauchy problem for the Camassa-Holm equation［J］.Nonlinear Anal Theory Methods Appl，2001，46:309－327.

［10］ Constantin A，Molinet L.Orbital stability of solitary waves for a shallow water equation［J］.Physica D:Nonlinear Phenomena，2001，157(1/2):75－89.

［11］ 杨灵娥，郭柏灵.浅水波方程的初边值问题［J］.数学理论与应用，2003，23:1－10.

Yang Linge，Guo Boling.Initial boundary value problem of shallow［J］.Mathematical Theory and Application，2003，23:1－10.(in Chinese)

［12］ Constantin A，StrassW A.Stability of the Camassa-Holm solitions［J］.JNonlinear Sci，2002，12:415－422.

［13］ Hakkaev S，Kirchev K.Local well-posedness and orbital stability of solitarywave solutions for the generalized Camassa-Holm equation［J］.Communications in Partial Differential Equations，2005，30(5/6):761－781.

［14］ Coclite GM，Holden H，Karlsen K H.Well-posedness of higher-order Camassa-Holm equation［J］.Journal of Differential Equations，2009，246(3):929－963.