基于最佳阻尼匹配的车辆悬架耗散功率的研究

刘小亭， 周长城， 高炳凯， 李 胜

(1.山东理工大学交通与车辆工程学院， 山东淄博 255091；2.淄博市交通运输监察支队， 山东淄博 255086；3.一汽解放青岛汽车有限公司， 山东青岛 266043)

现有车辆中普遍存在着能源的浪费现象[1]，如废气排放引起的振动能，汽车行驶过程中的振动能，以及制动时转化为热能的动能.在减少能源浪费的方案中，馈能悬架引起了国内、外车辆专家的高度关注.现有馈能悬架主要有静液蓄能式和电磁蓄能式[2].由于电磁式馈能悬架响应快，能量回收效率和执行精度高，而成为最理想的馈能方式[3].对于电磁式馈能悬架系统设计，必须首先确定悬架的功率，使悬架系统达到最佳阻尼匹配，满足车辆行驶平顺性的设计要求.据所查阅资料可知，由于受悬架系统阻尼匹配理论的制约，目前国内、外对于悬架功率一直未能给出可靠的设计理论和方法.例如，Wendel[4]等人研究了汽车悬架的能量再生系统，并给出了该系统的基本结构，Okada[5]教授利用双向电压变换电路和一个直线直流电机组成的阻尼作动器来吸收振动，国内喻凡教授则设计了滚珠丝杠结合永磁电机的馈能悬架，通过滚珠丝杠带动发电机发电，将动能转化为电能进行再利用.西南财经大学的蔡雷[6]，也只是通过最大速度与对应阻尼力确定悬架最大功率.这些研究虽给出了馈能悬架的结构模型，并对振动能量回收进行探讨，但是所确定的最大功率不能满足悬架阻尼匹配的要求，不能使车辆达到最佳减振效果.

本文首先通过单轮二自由度行驶振动模型对悬架系统最优阻尼比及最佳阻尼特性进行研究，然后依据悬架功率等于车载减振器单位时间所耗散能量，利用最佳阻尼特性数学模型，建立基于阻尼匹配的悬架功率设计数学模型，并通过设计实例及试验验证，从而解决制约馈能悬架设计的关键问题，使车辆达到最佳减振效果，提高车辆行驶平顺性.

1 单轮二自由度行驶振动模型及悬架最优阻尼比

1.1 单轮二自由度行驶振动模型

汽车单轮二自由度行驶振动模型[7]如图1所示，其中，单轮簧上质量为m2，簧下质量为m1，悬架阻尼为C；悬架弹簧刚度为K，轮胎刚度为Kt，q为路面不平度输入函数，z1、z2分别是车轮与车身垂直振动位移.

单轮二自由度系统的行驶振动微分方程可以表示为

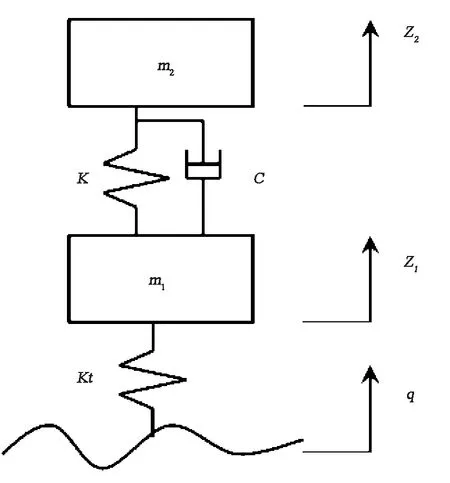
图1 单轮二自由度行驶振动模型

(1)

1.2 悬架最优阻尼比

为了便于分析，引入以下辅助变量：

由振动微分方程及根据随机振动理论[8]，可分别建立车身振动加速度响应和车轮动载荷的均方值数学模型[9]，即

(2)

(3)

式中，n0为参考空间频率，n0=0.1m-1；Gq(n0)为参考频率n0下的路面功率谱密度；v为车辆行驶速度.

(4)

(5)

根据基于舒适性的最佳阻尼比和基于安全性的悬架最佳阻尼比ζoc，利用黄金分割法ζos，可得到舒适性和安全性相统一的车辆悬架最优阻尼比ζo数学模型

ζo=ζoc+0.618(ζos-ζoc)

(6)

上式即为车辆悬架系统的最优阻尼比ζo，可使车辆达到最佳减振效果，满足车辆行驶平顺性的设计要求.

2 悬架最佳阻尼特性数学模型

2.1 复原行驶阻尼特性

已知悬架系统的固有频率fs，即

(7)

根据车辆参数、车身固有频率及最佳阻尼比ζo，可确定复原行程初次开阀阻尼系数

Ck1=4πζofsm2

(8)

由复原阀初次开阀速度Vk1及阻尼系数Ck1，可得初次开阀时的阻尼力和初次开阀前任意速度下的阻尼力

Fk1=Ck1Vk1

(9)

Fd=Ck1V

(10)

因为减振器在初次开阀前的阻尼系数Ck1，等于初次开阀前减振器速度特性曲线的斜率k1，由复原行程平安比η[10]，可得开阀后的特性曲线斜率为k2，即

k2=k1/ηps

(11)

根据开阀后的直线斜率k2和最大开阀速度点Vk2，可确定复原行程最大开阀阻尼力及最大开阀前任意速度下的阻尼力分别为

Fk2=Fk1+k2(vk2-vk1)

(12)

Fd=Fk1+k2(v-vk1)

(13)

2.2 压缩行驶阻尼特性

根据车辆参数以及压缩行程初次开阀阻尼系数Ck1y=Ck1=4πζofsm2[11]，压缩行程初次开阀速度Vk1y，可得压缩行程初次开阀前任意速度下的阻尼力和初次开阀时的阻尼力

Fd=Ck1yV

(14)

Fk1y=Ck1yVk1y

(15)

根据在相同速度情况下的减振器压缩与复原阻尼力的双向比β，可得压缩行程最大开阀阻尼力及最大开阀前任意速度下的阻尼力分别为

Fk2y=β[Fk1+k2(Vk2-Vk1)]

(16)

(17)

2.3 悬架最佳阻尼特性

根据复原和压缩行程的阻尼特性，可得悬架的分段速度特性曲线方程为

Fd=

3 悬架功率设计数学模型

3.1 减振器耗散功率数学模型

减振器示功图表示阻尼力随位移的变化曲线，所以曲线所围成的面积表示减振器一个循环周期内消耗的总功.减振器速度特性曲线表示阻尼力随速度的变化曲线，是由示功图求导得到，因此，曲线与坐标轴围成的面积S表示减振器消耗的功率.

设减振器复原和压缩最大速度分别为V2和V2y，则复原行程速度特性曲线与坐标轴围成的面积为

(19)

同理，压缩行程速度特性曲线与坐标轴围成的面积为

(20)

减振器在一个周期上、下振动循环过程中经过了复原和压缩两个行程，因此，减振器耗散功率可表示为

(21)

3.2 悬架功率数学模型

1)悬架最大功率。

由于悬架功率与减振器消耗的功率相等，所以当减振器速度对应悬架最大速度时，即V2=Vk2和V2y=Vk2y，则通过上式所得到的减振器最大耗散功率，即为悬架的最大功率设计值.

(22)

2)悬架额定功率.

当减振器速度对应车辆悬架常规速度时，则通过上式所得到的减振器耗散功率，即为悬架的额定功率设计值.

(23)

4 设计实例

某汽车悬架系统的单轮簧上质量m2=400kg；簧下质量m1=40kg；悬架弹簧刚度K=22 717N/m和轮胎刚度Kt=230 000N/m.在相同速度情况下的压缩阻尼力与复原阻尼力的双向比β=1/3，该汽车减振器的平安比ηps=1.5.

根据上述所建立的车辆悬架最优阻尼比数学模型，利用上述车辆参数，可求得基于舒适性的悬架最佳阻尼比ζc=0.164 8，基于安全性的阻尼比ζs= 0.436 9，以及舒适性和安全性相统一的悬架最优阻尼比ζo=0.333 0，并且建立车辆悬架最佳阻尼匹配速度特性数学模型，得到该车辆悬架的最佳阻尼特性曲线，如图2所示.

图2 匹配减振器的速度特性曲线

悬架最佳阻尼特性对应不同速度下所要求的阻尼力数值，见表1.

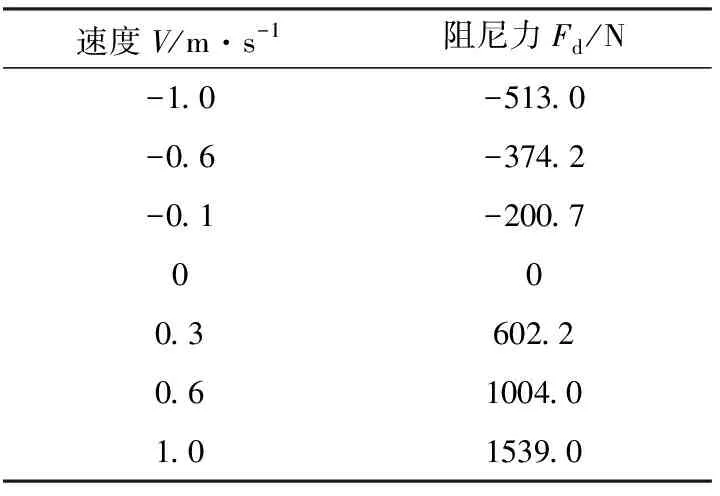
表1 速度特性值

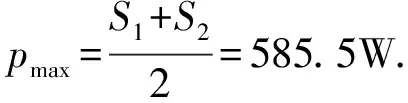
5 实验验证

利用电液伺服减振器综合性能试验台对所设计减振器的阻尼特性进行试验.该试验台的控制系统为数字控制和计算机控制的综合控制系统，可自动进行数据采集、处理、显示、打印数据和试验结果.其中，综合性能试验台，控制及数据采集系统，分别如图3和图4所示.

图3 电液伺服减振器综合试验台

图4 控制及数据采集处理系统

通过施加位移幅值为A=0.05m，频率分别为f=3.18Hz和f=1.909Hz的谐波激励信号，对减振器分别进行最大速度V=1.0m/s和常规速度V=0.6m/s下的特性试验.由试验测得的在不同加载频率下的减振器示功图，分别如图5中曲线1和曲线2所示.

图5 试验测得的在不同速度下的减振器示功图

由试验采集的数据，分别得到位移数组X={X(i)}和阻力数组Fd={Fd(i)}(i=1，2，3，…，N)，其中，N为一个周期循环所采集的数组个数.

已知试验的加载频率f，则利用位移数组X={x(i)}和阻尼力数组Fd={Fd(i)}，可求得减振器一个周期内消耗总功W，即

则减振器消耗的平均功率P，即

通过在最大速度V=1.0m/s下所测定的位移和阻尼力，利用Matlab分析计算程序，得该车辆所设计的原车载减振器的最大耗散功率为595.5W；在常规速度V=0.6m/s下，原车载减振器的额定耗散功率为246W.理论设计所得到的悬架最大功率和额定功率值与试验测得功率验证值的对比，如表2所示.

表2 悬架理论设计功率值与试验测得功率验证值的对比

由以上实例设计和试验验证可知，根据最优阻尼特性曲线所设计的悬架的最大功率和额定功率值，分别与所设计的车载减振器的耗散功率相吻合，其中，最大功率的相对偏差为1.7%，额定功率的相对偏差为1.4%.表明所建立的基于阻尼匹配的悬架功率的设计数学模型和方法是正确的.

6 结束语

通过理论分析、实例设计及试验验证，可知：通过车辆单轮行驶振动模型及分析，可建立基于舒适性和安全性的车辆悬架最优阻尼比及减振器最佳阻尼特性数学模型.根据减振器最佳阻尼特性数学模型，依据悬架的功率等于车载减振器单位时间所耗散能量，可以建立悬架最大功率和额定功率的设计数学模型.

3)实例设计及试验结果表明，所建立的悬架功率的设计数学模型的正确性，可使悬达到最佳阻尼匹配，为馈能悬架及发动机设计奠定了可靠理论基础.

[1] 王科星.汽车馈能式悬架技术研究[J].轻型汽车技术.2010(11/12):7-11.

[2] 于长淼,王伟华,王庆年.电磁馈能式悬架方案设计与节能分析[J],汽车技术,2010(2):21-24.

[3] 李志成.汽车馈能悬架的结构选型与性能仿真[D].长春:吉林大学汽车工程学院,2009.

[4] Wendel, Stecklein. A regenerative active suspension system[J]. SAE Publication SP-861,1991,95:129-135．

[5] Okada Y, Harada H. Regenerative control of active vibration damper and suspension system [C]// Proceedings of the 35th IEEE Conference on Decision and Control. Kobe, Japan: IEEE, 1996, 4:4 715-4 720.

[6] 蔡雷.汽车悬架能量回馈系统设计及控制研究[D].重庆：西南交通大学,2008.

[7] 周长城.汽车振动分析与测试[M].北京:北京大学出版社, 2011.

[8] 靳晓雄.汽车振动分析[M].上海:同济大学出版社, 2002.

[9] 周长城.汽车减振器设计与特性仿真[M].北京:机械工业出版社,2012.

[10] 周长城,孟婕,田立忠,等.汽车筒式减振器分段线性特性的建模与仿真[J].汽车工程,2010,32(4):333-339.

[11] 周长城,孟婕.车辆悬架最佳阻尼匹配减振器设计[J].交通运输工程学报,2008,8(3):15-19.