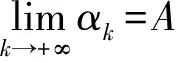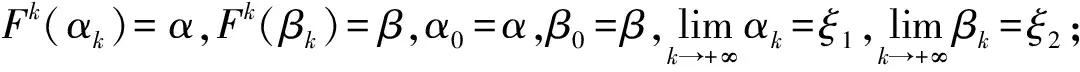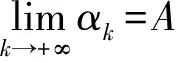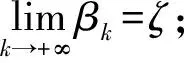一类有常值区间函数的迭代

成凯歌

(浙江旅游职业学院 基础部, 浙江 杭州 311231)

函数迭代的研究至今已经获得了许多重要成果[1-10].在对自然界的观察和科学技术的实验研究中，人们常常遇到这样的系统：系统在初始时刻t0状态可以决定以后的时刻t的状态，这样，时刻t的状态Xt便可看成时刻t0状态Xt0和差t-t0的函数Xt=F(t-t0,Xt0).要是每隔一个单位时间对系统作一次观测，则第n+1次观测到的状态Xtn+1=F(tn+1-tn,Xtn).由于tn+1-tn=1，所以Xtn+1=F(Xtn)，这里F(X)=F(1,X).于是Xtn+1=Fn+1(Xt0).这说明通过对F的迭代研究可以从t0时刻的状况分析系统在今后tn时刻的状况.另外计算机技术离不开迭代理论的指导，因为迭代最容易在计算机上进行[11].同时迭代还是一个普遍的现象，在X-射线的透射，流体的渗流等过程中都包含了迭代.在数学中，一切递推关系都是迭代，等差数列和等比数列就是迭代的产物[12].当自映射是严格单调时，其迭代情况最为简单，对于非单调自映射的迭代就会变得复杂起来了.本文将讨论一类有无穷多个非单调点的迭代问题，即有常值区间[13]的递增连续函数的迭代问题.

1 相关概念

在以下讨论中，设E=[0,1],k表示给定的任一非负整数，α,β∈(0,1)且α<β,F:E→E是一个连续自映射.F|S表示F在S上的限制,其中S⊆E.

定义1.1[14]记

F0(x)=x,Fk(x)=F(Fk-1(x)),

∀x∈E,k=1,2,…,

则Fk(x)对一切非负整数k都有定义.Fk称为F在E上的k次迭代函数.其中k称为迭代指数.

定义1.2[14]设x0∈E满足F(x0)=x0,则称x0是F的一个不动点或者称为一阶周期点.

明显地，若x0是F的一个不动点，则x0必是Fk的一个不动点.

定义1.3[15]设t0∈E是E的一个内点，如果存在t0的某个领域U(t0)，使得F在U(t0)上严格单调，则t0称为F的单调点.否则，t0称为F的非单调点.

定义1.4假如F在[α,β]上是一个常值函数，则称[α,β]是F的一个常值区间，或称F在[α,β]上是常值.

由定义可得，若[α,β]为F的一个常值区间，那么任意x∈[α,β]，x一定是F的非单调点.因此有常值区间的自映射必有无穷多个非单调点.

2 讨论过程

定义在E上并且以[0,α]和[β,1]为常值区间，[α,β]为严格递增区间的连续自映射全体记为C([0,α];[β,1]).为了便于表述，再令:=C([0,α];[β,1]);C1([0,α];[β,1])={F:F∈,F(β)≤α}；C2([0,α];[β,1])={F:F∈,F(α)≤α

定理2.1设F∈C(E),那么:1)Fk是E上的递增函数;2)Fk∈C(E).

证明1) 因为F∈C(E)是一个递增函数，而递增函数经过迭代运算之后依然是递增的，所以1)的结论是明显的.

为了证明2)的结论，分以下几种情况进行：

(i) 若F(x)=c,∀x∈E，则Fk(x)=c,∀x∈E，自然地Fk∈C(E).

(ii) 设F∈C([0,α];[β,1])并设k=i时结论成立.即Fi∈C(E).假如Fi(x)=c,∀x∈E，由

Fi+1(x)=c, ∀x∈E,

得到Fi+1∈C(E).假如Fi∈C([0,αk];[βk,1])，其中αi,βi∈E并且αi<βi以及α≤αi,βi≤β.如果Fi(αi)≥β或者Fi(βi)≤α，那么

Fi+1(x)=F(β), ∀x∈E,

Fi+1(x)=F(α), ∀x∈E,

必有其中一式成立.从而Fi+1∈C(E).如果α≤Fi(αi)

αi+1<βi+1,Fi(αi+1)=α,Fi(βi+1)=β.

并且当x∈[0,αi+1]时，Fi(x)≤α，当x∈(αi+1,βi+1)时，αβ.因此

Fi+1∈C([0,αi+1];[βi+1,1]),

即有Fi+1∈C(E).类似地可得，当α≤Fi(αi)<β

由上述定理的证明过程即可得到如下的推论.

推论2.1设F∈C([0,α];[β,1])，k为一任意正整数，记Fk∈C([0,αk];[βk,1]),那么:1) [0,α]⊆[0,αk],[β,1]⊆[βk,1];2)Fk(αk)≥F(α),Fk(βk)≤F(β);3) 当k≥2时，αk-1≤αk,βk≤βk-1,及4) 当k≥2时，Fk(αk)≥Fk-1(αk-1),Fk(βk)≤Fk-1(βk-1).这里记α1=α,β1=β.

推论2.1表明当F∈C([0,α];[β,1])时，F经过迭代之后它的常值区间不减.

定理2.2设F∈C1([0,α];[β,1]),那么当正整数k≥2时，Fk是E上的常值函数.

证明对∀x∈E，有F(x)∈[0,α].因此有F2(x)=F(α)对∀x∈E成立.从而有k≥2时，Fk是E上的常值函数.

定理2.3设F∈C2([0,α];[β,1]),那么当正整数k≥2时，有:

1) 若F在区间(α,β)内没有不动点并且F(α)<α，则存在正整数k0，使得当k≤k0时，Fk∈C([0,αk-1];[β,1])，其中αk-1满足Fk-1(αk-1)=α,α0=α；当k>k0时，Fk是E上的常值函数.

3) 若F(α)=α,则对任意正整数k，有Fk∈C2([0,α];[β,1]).

证明1) 因为F在区间(α,β)内没有不动点，从而ξ=F(α)是F的唯一不动点并且

因此必存在正整数k1，使得当k≤k1时，Fk(β)>α以及∃αk∈(α,β)使得Fk(αk)=α.当k>k1时，Fk(β)≤α.因此当k-1≤k1时有

Fk-1([0,αk-1])⊆[0,α],

Fk-1([αk-1,1])⊆[α,β].

因此对∀x∈[0,αk-1]有

Fk(x)=ξ<α<αk-1,

而Fk在[αk-1,β]上严格递增，对∀x∈[β,1]有

Fk(x)=Fk(β)>β.

所以当k≤k1+1时，Fk∈C([0,αk];[β,1]).因为Fk1+1(E)⊆E,所以当k>k1+1时，对∀x∈E有Fk(x)=F(α).因此令k0=k1+1就得要证结论.

2) 由假设可得存在α1∈(α,ξ)使得F(α1)=α.因为

F2(α1)=F(α)<α<ξ=F2(ξ).

所以又存在α2∈(α1,ξ)使得F2(α2)=α.如存在αi∈(αi-1,ξ)使得Fi(αi)=α,那么由

Fi+1(αi)=F(α)<α<ξ=Fi+1(ξ)

可知存在αi+1∈(αi,ξ)使得Fi+1(αi+1)=α.由归纳法可得{αk}满足

αk∈(αk-1,ξ),Fk(αk)=α.

3) 因为F(α)=α，所以对∀x∈[0,α]，都有Fk(x)=α；对∀x∈(α,1]，都有F(x)∈(α,β).从而Fk|[α,β]严格递增,Fk|[β,1]是常数并且ξ

定理2.4设F∈C3([0,α];[β,1])，记ξ1=min{x:F(x)=x,x∈[α,β]},ξ2=max{x:F(x)=x,x∈[α,β]},那么当正整数k≥2时有:

3) 当F(α)=α,F(β)=β时，则Fk∈C3([0,α];[β,1]);

证明因为F在[α,β]上必有不动点，所以ξ1,ξ2都存在.

1) 由假设可得ξ2=β,所以

Fk(x)=β,∀x∈[β,1].

又由假设可得∃α1∈(α,ξ1)使得F(α1)=α.因为

F2(α1)=F(α)<α<ξ1=F2(ξ1),

所以又存在α2∈(α1,ξ1)使得F2(α2)=α.如果存在αi∈(αi-1,ξ1)使得Fi(αi)=α.那么由

Fi+1(αi)=F(α)<α<ξ1=Fi+1(ξ1)

2) 因为F(α)<α,F(β)>β，所以α<ξ1≤ξ2<β.完全类似于1)中归纳法的证明可得存在αk,βk满足{αk}严格递增有界，{βk}严格递减有界，并且

Fk(αk)=α,Fk(βk)=β,

α<αk<ξ1≤ξ2<βk<β.

完全类似于定理2.3条件2)中的证明可得

除此之外，当x∈[0,αk-1]时，Fk-1(x)≤α；当x∈(αk-1,βk-1)时，α

3) 当x∈[0,α]时，Fk-1(x)≤α，当x∈(α,β)时，α

4) 类似于1)中所用归纳法可得存在{βk}关于k严格递减并且

βk∈(ξ2,βk-1),Fk-1(βk-1)=β.

Fk(x)=F(β)≥β≥βk-1.

当x∈(α,βk-1]时，α

定理2.5设F∈C4([0,α];[β,1])，那么Fk∈C4([0,α];[β,1]).

证明由F∈C4([0,α];[β,1])可得当x∈[α,β]时，总有Fk-1(x)∈(α,β).从而Fk|[α,β]是严格递增并且α

定理2.6设F∈C5([0,α];[β,1]),那么当正整数k≥2时有:

1) 若F在区间(α,β)内没有不动点并且F(β)>β，则存在正整数k0，使得当k≤k0时，Fk∈C([0,α];[βk-1,1])，其中βk-1满足Fk-1(βk-1)=β,β0=β；当k>k0时，Fk是E上的常值函数;

3) 若F(β)=β,则对任意正整数k，有Fk∈C2([0,α];[β,1]).

证明1) 因为F在区间(α,β)内没有不动点，从而ξ=F(β)是F的唯一不动点并且

因此必存在正整数k1，使得当k≤k1时，Fk(α)<β以及∃βk∈(α,β)使得Fk(βk)=β.当k>k1时，Fk(α)≥β.因此当k-1≤k1时有

Fk-1([βk-1,1])⊆[β,1],

Fk-1([0,βk-1])⊆[α,β].

因此对∀x∈[βk-1,1]有

Fk(x)=ξ>β>βk-1,

而Fk在[α,βk-1]上严格递增，对∀x∈[0,α]有

Fk(x)=Fk(α)>α.

所以当k≤k1+1时，Fk∈C([0,α];[βk,1]).因为Fk1+1(E)⊆E,所以当k>k1+1时，对∀x∈E,有Fk(x)=F(β).因此令k0=k1+1就得要证结论.

2) 由假设可得∃β1∈(ζ,β)使得F(β1)=β.因为

F2(β1)=F(β)>β>ζ=F2(ζ).

所以又存在β2∈(ζ,β1)使得F2(β2)=β.如存在βi∈(ζ,βi-1)使得Fi(βi)=β,那么由

Fi+1(βi)=F(β)>β>ζ=Fi+1(ζ)

可知存在βi+1∈(ζ,βi)使得Fi+1(βi+1)=β.由归纳法可得{βk}满足

βk∈(ζ,βk-1),Fk(βk)=β,

3) 因为F(β)=β，所以对∀x∈[β,1]，都有Fk(x)=β；对∀x∈[0,β)，都有F(x)∈(α,β).从而Fk|[α,β]严格递增,Fk|[0,α]是常数并且Fk(α)>α.由此得Fk∈C2([0,α];[β,1]).

定理2.7设F∈C6([0,α];[β,1]),那么当k≥2时，Fk是E上的常值函数.

证明注意到F(β)是F的唯一不动点，并且对任意x∈E，有F(x)∈[β,1].因此有F2(x)=F(β)对∀x∈E成立.从而有k≥2时，Fk是E上的常值函数.

[1] Abel N H. Oeuvres Completes[M]. Christiania,1881,II:30-47.

[2] Bödewadt U T. Zur iteration reeller funktionen[J]. Math Z,1944,49:90-523.

[3] Zdun M C. On the iteration of the hat-functions[J]. Aequationes Math,1977,16:181-182.

[4] Blokh A, Coven E, Misiurewicz M, et al. Roots of continuous piecewise monotone maps of an interval[J]. Acta Math Univ Comenian,1991,60:2-9.

[5] Targonski G. Progress of iteration theory since 1981[J]. Aequationes Math,1995,50:50-72.

[6] Bogatyi S. On the nonexistence of iterative roots[J]. Topology Appl,1997,76(2):93-122.

[7] Jarczyk W, Powierza T. On the smallest set-valued iterative roots of bijections[J]. Inter J Bifur Chaos Appl Sci Engrg,2003,13(7):1887-1898.

[8] Shi Y Y. Convergence of fixed point iteration for modified restoration problems[J]. J Math Imaging Vision,2008,32(1):31-39.

[9] Marchenkov S S. Iteration operators on a set of continuous functions of Baire space[J]. Moscow University Computational Mathematics and Cybernetics,2011,35(4):184-188.

[10] Krassowska D, Zdun M C. On iteration group of diffeomorphisms with two fixed points[J]. J Math Anal Appl,2011,382(1):204-213.

[11] 张景中，熊金城. 函数迭代与一维动力系统[M]. 成都:四川科技教育出版社,1992:1-6.

[12] 张伟年. 动力系统基础[M]. 北京：高等教育出版社,2001:1-4.

[13] 张广远. 一类线段自映射的共轭与迭代根[J]. 数学年刊,1992,A13(4):473-478.

[14] Kuczma M, Choczewski B, Ger R. Iterative Functional Equations[M]. Cambridge:Cambridge Univ Press,1990.

[15] 张景中,杨路. 论逐段单调连续函数的迭代根[J]. 数学学报,1983,26(4):398-412.