耗散SLRW方程的一个新的守恒差分逼近

林雪梅, 胡劲松, 刘 倩

(西华大学 数学与计算机学院, 四川 成都 610039)

在研究弱非线性离子声波和空间带电波的传播时,文献[1]提出了对称正则长波(SRLW)方程

uxxt-ut=ρx+uux,

(1)

ρt+ux= 0.

(2)

关于SRLW方程(1)、(2)的定解问题的适定性及数值方法的研究也引起了广泛关注[2-5].但在实际问题中,粘性耗散是不可避免的,且与色散一样起着十分重要的作用.因此,本文考虑如下一类具有耗散项的SRLW方程的初边值问题

uxxt-ut+βuxx=ρx+uux,

(3)

ρt+ux= 0,

(4)

u(x,0)=u0(x),ρ(x,0)=ρ0(x),

x∈[xL,xR],

(5)

u(xL,t)=u(xR,t)=0,ρ(xL,t)=ρ(xR,t)=0,

t∈[0,T],

(6)

其中β是耗散系数.不难证明,该问题具有如下守恒律

(7)

(8)

在考虑耗散时,方程(3)和(4)是反映非线性离子声波运动本质现象的合理模型[6].文献[6-10]分别讨论了方程(3)和(4)的解的适定性和整体存在唯一性以及解的长时间性态等,但其解析解很难求出,于是,研究其定解问题的数值解就很有意义.如果计算精度较高,而且还能模拟问题本身的守恒性质,无疑是最理想的数值方法[2-4,9-10].文献[11-12]对(3)～(6)式分别提出了一个具有二阶精度的2层非线性差分格式和3层线性差分格式,文献[13-14]又进一步对带有阻尼项的耗散SRLW方程进行了数值研究,但都没有考虑问题的守恒律(7)和(8)式.本文利用Lax格式的离散思想,在保持二阶理论精度的情况下,引入加权系数a,对问题(3)-(6)提出了一个3层线性的加权差分格式,格式合理地模拟了(7)和(8)式,从而适合长时间计算.由于格式是线性的,数值求解是不需要迭代,计算时间比较节约;数值算例表明,通过适当地调整加权系数a,从而使计算结果比文献[12]中的二阶格式具有更高精度.

1 守恒律和差分解估计

(9)

(10)

(9)～(12)式对(7)和(8)式的数值模拟得定理1.

定理1(9)～(12)式关于离散能量守恒

(13)

(14)

证明(9)式两端乘以h后对j求和,结合(12)式和(3)式,可得

递推可得(13)式.

同理,对(10)式两端乘以h后对j求和,然后递推可得(14)式.

定理2设u0∈H1,ρ0∈L2,则(9)～(12)式的解满足:‖un‖ ≤C,‖uxn‖ ≤C,‖ρn‖ ≤C,‖un‖∞≤C(n=1,2,…,N).

(15)

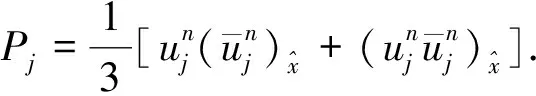
(17)

(18)

将(15)与(18)式相加,并结合(16)和(17)式得

令

a(‖ρn+1‖2+‖ρn‖2),

将上式递推可得

Bn≤Bn-1≤ …≤B0=C,

又

则

(a-|1-a|)(‖un+1‖2+‖un‖2)+

(‖ρn+1‖2+‖ρn‖2) ≤Bn≤C,

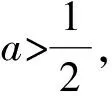
由离散的Sobolev不等式[3]得

‖un‖∞≤C.

2 差分格式的收敛性和稳定性

(20)

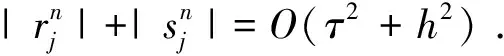
定理3设u0∈H1,ρ0∈ L2,则差分格式(9)～(12)式的解un以‖·‖∞,ρn以‖·‖L2收敛到初边值问题(3)～(6)式的解,且收敛阶为O(τ2+h2).

(22)

(23)

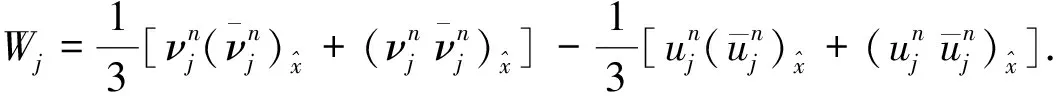
(24)

由定理2以及Schwraz不等式得

‖en+1‖2+‖exn+1‖2+‖exn-1‖2),

(25)

又

(26)

(27)

再将(24)和(27)式相加,并结合(25)和(26)式,令

有

Dn-Dn-1≤τ‖rn‖2+τ‖sn‖2+Cτ(‖en+1‖2+

(28)

将(28)式从1到n求和有

(29)

其中

T·O(τ2+h2)2,

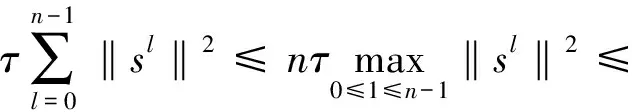
T·O(τ2+h2)2,

先用2层格式[11]计算出u1和ρ1,使之满足D0≤O(τ2+h2)2,又类似(19)式有

(‖ηn+1‖2+‖ηn‖2)

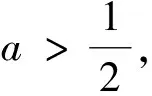
‖ηn‖≤O(τ2+h2),

再由(3)式有

‖en‖∞≤O(τ2+h2).

与定理3类似,可以证明定理4.

定理4在定理3的条件下,差分格式(9)～(12)式的解un以‖·‖∞,ρn以‖·‖L2稳定.

3 数值实验

在t=0时,由于耗散还没有产生,所以在数值实验中,把(3)～(6)式中的初值函数取为SRLW方程(1)和(2)的初值函数[11](t=0时)

固定-xL=xR=20,T=1.0,取β=1.由于方程(3)和(4)的精确解并不知道,用类似文献[11]中的误差估计方法,将细网格(τ=h=1/160)上的数值解作为精确解来估计误差,就τ和h的不同取值时,几个不同时刻的l∞误差(表1～2),及对守恒量的模拟(表3和4).

当加权系数a=1时,本文的格式即为文献[14]中的格式.数值结果表明,加权系数a(a>1/2)取得越小,计算精度越高,特别当a=1/2时,计算精度比文献[14]中的格式的计算精度有大幅度提高;另外格式对守恒量(7)和(8)式也进行了很好的模拟,故本文的格式是有效的.

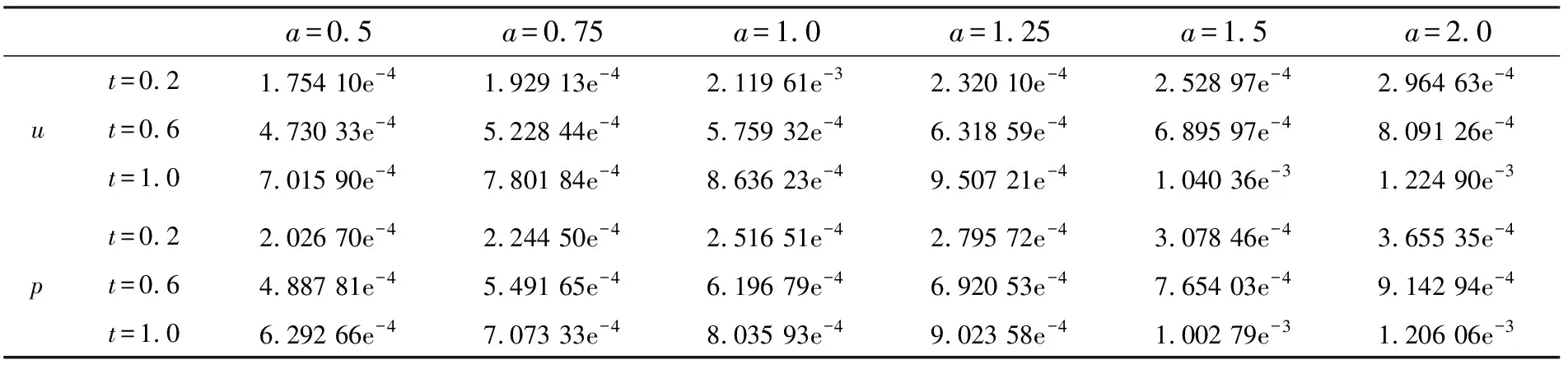
表 1 τ=h=0.05时,就不同的参数a,在几个不同时刻的l∞误差Table 1 The error at various time step in norm ‖·‖∞ with τ=h=0.05

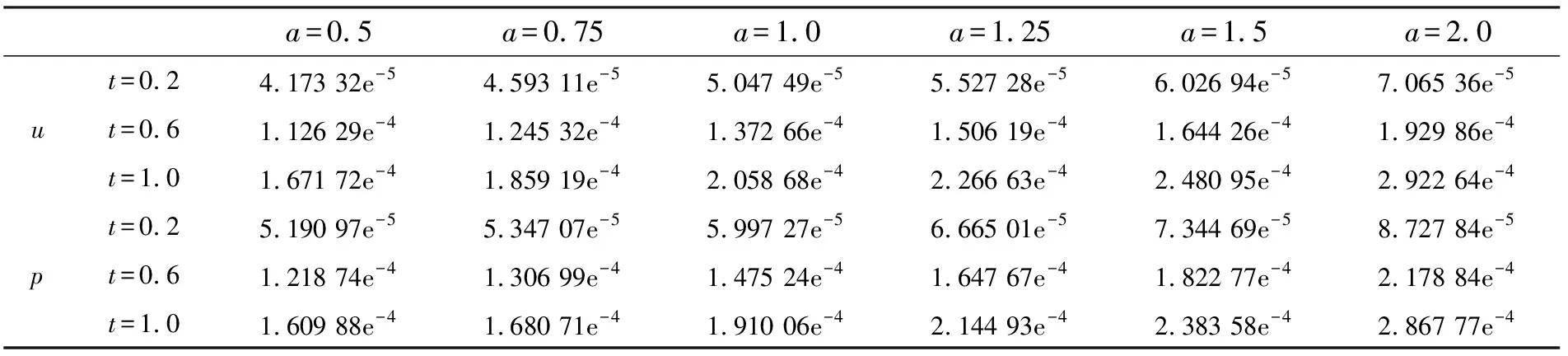
表 2 τ=h=0.025时,就不同的参数a,在几个不同时刻的l∞误差Table 2 The error at various time step in norm ‖·‖∞ with τ=h=0.025

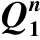
表 3 在不同时刻对守恒量(7)和(8)式的数值模拟和Table 3 Numerical simulations on two conservation invariants and with τ=h=0.05

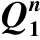
表 4 在不同时刻对守恒量(7)和(8)式的数值模拟和Table 4 Numerical simulations on two conservation invariants and with τ=h=0.025

致谢西华大学研究生创新基金(YCJJ201311)对本文给予了资助,谨致谢意.

[1] Seyler C E, Fenstermacler D C. A Symmetric regularized long wave equation[J]. Phys Fluids,1984,27(1):4-7.

[2] Wang T C, Zhang L M, Chen F Q. Conservative schemes for the symmetric regularized long wave equations[J]. Appl Math Comput,2007(190):1063-1080.

[3] 柏琰,张鲁明. 对称正则长波方程的一个守恒差分格式[J]. 应用数学学报,2007,30(2):248-255.

[4] 王廷春,张鲁明. 对称正则长波方程的拟紧致守恒差分逼近[J]. 数学物理学报,2006,A26(7):1039-1046.

[5] Guo B L, Shang Y D. Approximate inertial manifolds to the generalized symmetric regularized long wave equations with damping term[J]. Acta Math Appl Sinica,2003,19(2):191-204.

[6] Shang Y D, Guo B L, Fang S M. Long time behavior of the dissipative generalized symmetric regularized long wave equations[J]. J Partial Diff Eqns,2002(15):35-45.

[7] 尚亚东,郭柏灵. 耗散的广义对称正则长波方程周期初值问题的整体吸引子[J]. 数学物理学报,2003,A23(6):745-757.

[8] Fang S M, Guo B L, Qiu H. The existence of global attractors for a system of multi-dimensional symmetric regularized long wave equations[J]. Commun Nonlinear Sci Numer Simulat,2009(14):61-68.

[9] 刘利斌,刘焕文,余锦鸿. 四阶抛物型方程子域精细积分紧致差分格式[J]. 重庆师范大学学报:自然科学版,2008,25(3):24-27.

[10] 刘桂利,刘利斌. 四阶抛物型方程的样条子域精细积分配置法[J]. 重庆师范大学学报:自然科学版,2007,24(4):33-36.

[11] 胡劲松,胡兵,徐友才. 耗散对称正则长波方程的有限差分逼近[J]. 计算数学,2011,33(2):177-184.

[12] 胡劲松,胡兵,徐友才. 耗散对称正则长波方程的平均隐式差分格式[J]. 高等学校计算数学学报,2012,34(4):300-307.

[13] Hu J S, Xu Y C, Hu B. A linear difference scheme for dissipative symmetric regularized long wave equations with damping term[J/OL]. Mathematical Problems in Engineering,2010,http://www.researchgate.net/publication/50282553.

[14] Hu J S, Hu B, Xu Y C. C-N difference schemes for dissipative symmetric regularized long wave equations with damping term[J/OL]. Mathematical Problems in Engineering,2011,http://dx.doi.org/10.1155/2011/651642.