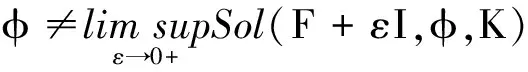广义混合变分不等式的Tikhonov正则化方法

付冬梅, 何诣然

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

广义混合变分不等式(简称GMVI(F,φ,K))是指寻找x∈K和x*∈F(x)满足

〈x*,y-x〉+φ(y)-φ(x)≥0, ∀y∈K,

在文献[1-4]中,广义变分不等式已经被广泛研究,Tikhonov正则化方法是解决不适定变分不等式解存在的一种重要方法,而在文献[5]中已经用Tikhonov正则化方法讨论了不适定广义变分不等式解的存在性问题.广义混合变分不等式是广义变分不等式的推广,本文用Tikhonov正则化方法来研究广义混合变分不等式解的存在性.

作为准备,首先给出了GMVI(F,φ,K)解存在的一个结论:如果F是具有非空紧凸值的上半连续集值映象,K是紧凸集,则GMVI(F,φ,K)有一个解.如果K不是紧集,GMVI(F,φ,K)解的存在性通常要求额外的强制条件.研究者试图寻找尽可能弱的强制条件.本文给出了几种常用的强制条件,并证明了(A)是几种强制条件中最弱的.定理2.5证明了如果(F,φ)具有混合变分不等式性质,而且强制条件(A)成立,则GMVI(F,φ,K)有一个解.而当F是具有非空紧凸值的集值映象,φ是真凸下半连续泛函时,(F,φ)具有混合变分不等式性质.最后建立了广义混合变分不等式的Tikhonov正则化结果.

1 预备知识

除非特别说明,文中总是假设K⊂Rn是一个非空闭凸集,F:K→2Rn是一个非空集值映象,φ：K→R∪{+∞}是真凸下半连续泛函.对∀r>0,Kr:={x∈K:‖x‖≤r};对∀ε>0,Aε⊂Rn,有

有εn→0+,xn∈Aεn且xn→x}.

定义1.1设F:K→2Rn是一个非空集值映象.1)F称为是单调的,如果对∀x,y∈K及∀x*∈F(x),y*∈F(y),〈y*-x*,y-x〉≥0. 2)F称为是拟单调的,如果对∀x,y∈K及所有的x*∈F(x),y*∈F(y),〈x*,y-x〉>0⟹〈y*,y-x〉≥0. 3)F称为在x∈K处上半连续,如果对于F(x)的任一邻域V,都存在x的邻域U使得对所有的y∈K∩U有F(y)⊂V;如果F在每一个x∈K处上半连续,则称F在K上上半连续.4)F称为沿线结上半连续,如果F沿K的每一个线节上半连续.

命题1.2如果F是具有紧凸值的集值映象,φ是真凸下半连续泛函,那么

1) 存在x∈K和x*∈F(x)使得对∀y∈K,〈x*,y-x〉+φ(y)-φ(x)≥0;

2)⟹1)令φ(x*,y)=〈x*,y-x〉+φ(y)-φ(x).则x*→-φ(x*,y)是下半连续的凸泛函,y→-φ(x*,y)是凹泛函.因为F是具有紧凸值的集值映象,由文献[6]中Sion极大极小定理得

即

由2)成立,即

∀y∈K.

存在x*∈F(x)使得

〈x*,y-x〉+φ(y)-φ(x)≥0, ∀y∈K.

定理1.3如果K是Rn中的紧凸集,F:K→2Rn是具有非空紧凸值的上半连续映象,φ:K→R∪{+∞}是真凸下半连续泛函,则GMVI(F,φ,K)有解.

∀y∈K.

即存在x∈K使得

∀y∈K,

即GMVI(F,φ,K)有解.

2 解的存在性和强制条件

定义2.1如果对K中每一个非空有界闭凸集D,GMVI(F,φ,D)有解,则称(F,φ)有混合变分不等式性质.

命题2.2F是具有非空紧凸值的上半连续集值映象,φ是真凸下半连续泛函,那么(F,φ)具有混合变分不等式性质.

证明因为Rn中有界闭凸集为紧凸集,所以由定理1.3可得结论.

命题2.3如果F:K→2Rn是具有非空紧凸值的上半连续映象,T:K→2Rn是单调且具有非空紧凸值的沿线结上半连续映象,φ1、φ2:K→R∪{+∞}为真凸下半连续泛函,则(F+T,φ1+φ2)有混合变分不等式性质.

证明设D⊂K为有界闭凸集,定义G,H:D→2D为

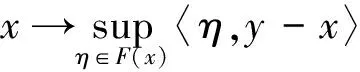
(φ1+φ2)yi-(φ1+φ2)y0<0,

又因为

(φ1+φ2)y0-(φ1+φ2)y0=

(φ1+φ2)yi-(φ1+φ2)y0),

与

(φ1+φ2)yi-(φ1+φ2)y0<0

两边同时除以t>0则有

进而

让t→0+,由T是上半半连续映象可得,对∀y∈D有

即对∀y∈D有

考虑下面几种强制条件之间的关系:

(C) 存在r>0使得∀x∈KKr,∀x*∈F(x),存在y∈kr满足〈x*,x-y〉-φ(y)+φ(x)>0;

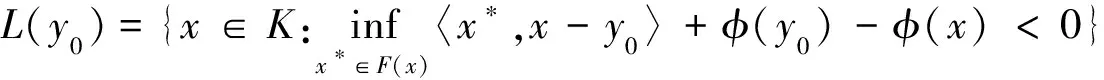
命题2.41) 如果F是具有凸值的集值映象,则(C)⟹(B).2) 如果F是拟单调的,则(D)⟹(B).3) (E)⟹(B)⟹(A).

证明1) 由(C)成立知∀x∈KKr有

因为F(x)是凸值的,Kr是紧凸集,由文献[6]中Sion极大极小定理可知

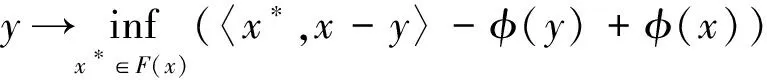
则(B)成立.

〈y*,x-y〉-φ(y)+φ(x)>0.

又F是拟单调的,所以对∀x*∈F(x),

〈x*,x-y〉-φ(y)+φ(x)≥0,

即

3) (E)⟹(B) 如果L(y0)=Φ,则对∀x∈K有

如果L(y0)≠Φ,则存在r使得L(y0)∪{y0}⊂Kr,对∀x∈KKr,y0∈K满足‖y0‖<‖x‖且

即(B)成立.

(B)⟹(A)设r为(B)成立的r,则对∀x∈KKr+1,存在y∈Kr使得

且‖y‖≤r

定理2.5设K⊂Rn是一个非空闭凸集,F:K→2Rn是具有非空紧凸值的集值映象,φ:K→R∪{+∞}是真凸下半连续泛函.假设强制条件(A)成立且(F,φ)有混合变分不等式性质,则GMVI(F,φ,K)有解.

证明设m>r,由于Km是有界闭凸集且(F,φ)有混合变分不等式性质,则存在xm∈Km使得对∀y∈Km存在

如果‖xm‖=m,则‖xm‖>r.由(A)成立可知存在y0∈K满足‖y0‖<‖xm‖=m且

由于‖y0‖

(1-t)(y0-xm)〉+φ(y0+t(y-y0))-φ(xm)≤

tφ(y)+(1-t)φ(y0)-φ(xm)≤

两边同时除以t,则对∀y∈K,

如果‖xm‖

两边同时除以t,则对∀y∈K,

推论2.6设K⊂Rn是一个非空闭凸集,F:K→2Rn是具有非空紧凸值的上半连续集值映象,φ:K→R∪{+∞}真凸下半连续泛函,如果(A)成立,则GMVI(F,φ,K)有解.

证明由命题2.2和定理2.5可得结论.

3 Tikhonov正则化

定理3.1设K⊂Rn是非空闭凸集,F:K→2Rn是具有非空紧凸值的上半连续集值映象,φ:K→R∪{+∞}真凸下半连续泛函,如果(A)成立,则对∀ε>0,1)GMVI(F+εI,φ,K)有解;2) 集合A={Sol(F+tI,φ,K):t∈(0,ε]}有界.

证明1) 由(A),对∀x∈KKr,存在y∈K满足‖y‖<‖x‖且

又因为

ε〈x,x-y〉≥ε‖x‖2-ε‖x‖‖y‖≥0.

即对∀x∈KKr,存在y∈K满足‖y‖<‖x‖,

则(F+εI,φ)满足条件(A).又由F是具有非空紧凸值的上半连续集值映象,I是连续单调映象,φ是真凸下半连续泛函,所以由命题2.3和定理2.5,GMVI(F+εI,φ,K)有解.

2) 设t∈(0,ε],x(t)∈Sol(F+tI,φ,K),下证x(t)∈Kr.若x(t)Kr,则存在y(t)∈K满足‖y(t)‖<‖x(t)‖且

φ(y(t))+φ(x(t))≥0,

又由x(t)∈Sol(F+tI,φ,K)且y(t)∈K,则

φ(y(t))+φ(x(t))=

t‖x(t)‖2-t〈x(t),y(t)〉-φ(y(t))+φ(x(t))≥

t‖x(t)‖2-t‖x(t)‖‖y(t))‖

与‖y(t)‖<‖x(t)‖矛盾.

证明设r>0且满足

φ(y)+φ(x))<0}⊂Kr,

则∀x∈KKr有

由于y0∈D⊂Kr,则‖y0‖

εn‖xn‖2+φ(y)-φ(xn).

又因为

-εn‖xn‖2+φ(y)-φ(xn))≤

〈x*,y-x〉+φ(y)-φ(x),

故对∀y∈K,〈x*,y-x〉+φ(y)-φ(x)≥0,从而x∈Sol(F,φ,K).

致谢四川师范大学研究生优秀论文培育基金项目(校研字201314-35)对本文给予了资助,谨致谢意.

[1] Fang S C, Peterson E L. Generalized variational inequalities[J]. J Optim Theory Appl,1982,38(3):363-383.

[2] Daniilidis A, Hadjisavvas N. Coercivity conditions and variational inequalities[J]. Math Programming,1999,A86(2):433-438.

[3] He Y R. Stable pseudomonotone variational inequality in reflexive Banach spaces[J]. J Math Anal Appl,2007,330(1):352-363.

[4] Qiao F S, He Y R. Strict feasibility of pseudomonotone set-valued variational inequalities[J]. Optimization,2011,60(3):303-310.

[5] He Y R. The Tikhonov Regularization Method for Set-Valued Variational Inequalities[J/OL]. Abst Appl Anal,2012,http://dx.doi.org/10.1155/2012/172061.

[6] Sion M. On general minimax theorems[J]. Pacific J Math,1958,8(1):171-176.

[7] Aubin J P, Ekeland I. Applied Nonlinear Analysis[M]. Toronto:John Wiley & Sons,1984.

[8] 张石生. 变分不等式及其相关问题[M]. 重庆:重庆出版社,2008.

[9] Facchinei F, Pang J S. Finite-Dimensional Variational Inequalities and Complementarity Problems[M]. New York:Springer-Verlag,2003.

[10] 何诣然. 具有集值映射变分不等式的理论分析[J]. 四川师范大学:自然科学版,2010,33(6):840-848.

[11] 刘智,何诣然. 集值变分不等式解的存在性问题[J]. 四川师范大学:自然科学版,2010,33(2):156-158.

[12] 刘智,何诣然. Banach空间集值变分不等式解的存在性[J]. 四川师范大学:自然科学版,2011,34(5):621-624.

[13] 何诣然. KKM定理,极小极大不等式的推广和应用[J]. 四川师范大学:自然科学版,1998,21(2):154-158.

[14] 王敏,何诣然. Banach空问中集值映射的广义变分不等式问题[J]. 四川师范大学:自然科学版,2006,29(4):447-449.

[15] 薛建明. 拟Banach空间正交的右存在性和左存在性[J]. 重庆师范大学学报:自然科学版,2012,29(5):50-52.

[16] 赵勇,赵克全,廖伟. 集值映射向量优化的近似Benson真有效性[J]. 重庆师范大学学报:自然科学版,2013,30(2):7-9.