快速成型中基于MATLAB软件的STL模型的分层优化

王春香，郝志博，陈浩宏

(1.内蒙古科技大学机械学院，内蒙古包头014010;2.包头市万佳信息工程有限公司，内蒙古包头014010)

0 前言［1－8］

STL 格式的模型为大多数快速成型设备所接受，其分层算法的好与坏直接影响到快速型成技术的精度要求和制造效率，直接制约着零件的实用性和投产，因此快速成型技术的分层算法成为了研究热点。

按照对三角形面片的信息利用方式的不同可以将三角形面片的分层算法分为以下3 类:

(1)基于三角形面片位置信息的分层算法。这种算法是按照三角形面片中的顶点坐标z 值的大小对STL 模型进行排序，将不同的三角形面片按照顶点z值坐标上的最小值和最大值从小到大进行分类排序，以便于减少三角形面片与分层切平面的位置判断次数，提高分层的效率。但是分类排序过程中类的划分十分模糊，不能完全杜绝位置关系无效判定;而且分层过程中类的划分也十分耗时。

(2)基于三角形面片的拓扑信息的分层算法。该算法是根据三角形面顶点坐标依次建立点、线、面的链表或者根据平衡二叉树对STL 模型建立整体的拓扑信息，使得相邻的三角形面片之间具有毗邻关系，当分层切平面与一个三角形面片相切时，便可以通过三角形面片的毗邻关系依次查找出其他与该分层切平面相交的三角形面片，最后按顺序输出分层轮廓线。该方法的局限性在于对模型建立拓扑关系非常耗时，尤其在模型数据量较大时十分耗费内存资源。

(3)基于三角形面片的局部拓扑信息的分层算法。这种算法是针对上述两种算法的改进，用以提高三角形面片的搜索效率。该算法首先建立一个三角形面片集，然后将与某一层分层切平面相交的三角形面片动态地储存在该集合中，当分层切平面从上一层到下一层时，把不与该层相交的三角形面片从集合中剔除，将与该层相交的新三角形面片加入集合，然后对这些在集合中的三角形面片建立局部的拓扑关系，进行求交运算，最终输出该层的轮廓线。该算法局限性在于集合中动态储存三角形面片和局部拓扑关系的建立仍是比较费时的工作。

面向STL 模型的分层切片算法要求分层程序具有较高的稳定性和时效性。本文作者提出一种基于三角形面片的排序精简方法，提取只与分层切平面相交的三角形面片，提高了分层效率，尤其是在数据量较大的模型下，其高效性更为突出，而且经过多次验证该算法具有较高的稳定性。

1 算法的基本思想

该算法在总结分析以上优点，得出以下的结论:基于三角形面片在分层方向上的最大值和最小值的不同，最小值小的先被切到，而最小值大的后被切到;当三角形面片的最小值大于该分层切平面的高度值或者当三角形面片的最大值小于该分层切平面的高度值时都不会与该分层切平面相交;相邻的两个分层切平面相交的三角形面片集合之间变化很小。依据这些原理，对STL 模型中的三角形面片进行剔除和排除，用以精简数据，直接提取出只与分层截面相交的三角形面片，最后将分切层平面与每个三角面片进行求交运算，无需建立三角形面片之间的拓扑关系，直接输出分层截面轮廓线。

2 算法实现的基本过程

应用MATLAB 软件的强大矩阵逻辑运算功能，快速地实现了该算法。该算法具体实现过程如下:

2.1 数据的读取

由于STL 模型数据是由字符串与数值混合在一起，所以必须对模型中每一个三角形面片的3 个顶点坐标以及三角形面片法向量坐标进行提取。通过整行读取的形式对STL 模型数值数据进行提取，即对STL模型中的数据一行一行读取，然后采用不同限定条件对模型中三角形面片数据中的顶点坐标和法向量坐标分别提取，最终用两个矩阵分别对应表示出所有三角形顶点坐标以及向量坐标。其表示形式如下:

datatri= ［v1x v1y v1z;v2x v2y v2z;v3x v3y v3z;…］

datan= ［ni nj nk;…］

其中“;”代表每一行的分隔符，“datatri”代表三角形面片顶点坐标矩阵，“datan”代表三角形面片法向量坐标矩阵。每三行顶点坐标与一行法向量坐标相对应组成一组数据，这么一组对应数据表示一个三角形面片。这样STL 模型的读取初步完成。

2.2 数据的整合和第一次排序

数据的整合包括两个部分:(1)将每一个三角形面片的3 个顶点坐标进行整合;(2)STL 模型中三角形面片顶点矩阵与三角形面片法向量矩阵的整合。三角形面片的顶点矩阵与法向量矩阵的整合是以三角形面片的3 个顶点坐标的整合为基础的，将这些数据整合后使得每一个三角形面片的信息储存在一个矩阵中的一行内，便于后续过程的需要。

(1)第一次数据整合

由于MATLAB 中的运算都是按一列一列顺序进行，而读取STL 模型数据的每一个顶点坐标都是按行提取的，若要整合一个三角形面片的3 个顶点坐标则必须将其作一次转置，使之成为3 行n 列的矩阵，其表示形式如下:

datatri’ = ［v1x v2x v3x…vnx;v1y v2y v3y…vny;v1z v2z v3z…vnz］

将转置后的矩阵转换为9 行n/3 列的矩阵。这样完成了三角形面片3 个顶点坐标的整合，转换后的矩阵中的每一列代表一个三角形面片的3 个顶点。

(2)第一次排序

整合三角形面片的3 个顶点坐标后，为了后续的排序方便，在三角形面片的顶点矩阵与法向量矩阵整合之前，先对STL 模型中的每一个三角形面片顶点进行第一次排序，对模型的每一个三角形面片的3 个顶点按照其在分层方向上的分量的大小进行升序排列。这个过程在MATLAB 中的具体实现为:将第一次整合后的矩阵进行转置，将其转换为n/3 行9 列矩阵，依次提取矩阵中的每一行，将其转换为3 行3 列矩阵，对该3 行3 列矩阵进行转置，按照其中的某一列三值的大小对矩阵排序。(这样就把每一个三角形面片划分了出来，然后根据顶点坐标在分层方向上分量的大小对三角形面片的3 个顶点进行第一次排序。)排序后将3 行3 列矩阵转置，然后将其转换为一行。一行一行地将其输出，组成一个n/3 行9 列的矩阵。(这样将顶点排序后的每一个三角形面片放回到了原位置，该操作不仅完成了三角形面片的排序，而且输出的矩阵可以直接和对应的法向量矩阵相结合组成三角形面片矩阵)这个n/3 行9 列的矩阵表示形式为:

datatrinew= ［v1x v1y v1z v2x v2y v2z v3x v3y v3z;…］

其中“v1x v1y v1z v2x v2y v2z v3x v3y v3z”是排序完成以后的3 个顶点坐标，并且每个三角形面片的3 个顶点的坐标处在该矩阵中的一行。

(3)第二次整合

第二次整合，即三角形面片的3 个顶点坐标矩阵与法矢量矩阵的整合。将第一次排序完成的三角形面片顶点坐标矩阵和三角形面片法向量坐标矩阵进行对应合并。由于在第一次整合和第一次排序过程中，本文始终没有打乱三角形面片顶点坐标矩阵和三角形面法向量坐标矩阵的对应关系。所以对于这一次的整合就变得十分简单，其表示形式如下:

data= ［datan，datatrinew］= ［ni nj nk v1x v1y v1z v2x v2y v2z v3x v3y v3z;…］

整合和第一次排序后的矩阵能够完整地表示STL模型的几何信息，而且使得原有的STL 模型数据得到精简，经过第一次的坐标排序以后，使得每一个三角形面片的顶点坐标变得有序化，为后期的排序节省了许多时间，对后续工作的完成十分重要。

2.3 数据的分层排序过程

(1)第二次排序和数据的删除

经过数据整合和第一次的排序，虽然三角形面片在模型的整体矩阵中仍以散乱的方式储存，但是每一个三角形面片却有规律可循了。因此对模型的整体矩阵进行排序精简，用以达到对模型的快速分层要求。

每一个三角形面片顶点的坐标按照其在分层方向上分量的大小进行了升序排列，且每一个三角形面片的所有数据都在矩阵中的一行，那么按照三角形面片顶点坐标在分层方向上的最大值的大小对整合后的整个矩阵进行升序排列，这样STL 模型中的三角形面片的第二次排序进行完成。

如果三角形面片在分层方向上的最大值小于某一分层切平面，那么说明该三角形面片就不会与该分层切平面相切，由于STL 模型分层处理时是按照分层平面由小到大进行切割，那么该三角形面片也不会与以后的分层切平面相交，这样可以直接剔除该三角形面片，以便减少内存的占有量。

三角形面片第二次排序在MATLAB 中实现方式:将整合后的矩阵按照其中一列的数值大小进行升序排序(这一列的数值是每一个三角形面片顶点坐标在分层方向上的最大值，也就是按照每个三角形面片顶点在分层方向的最大值的大小进行升序排序)。

剔除三角形面片的过程在MATLAB 中实现方式:将整理后的那一列中所有小于分层切平面高度值的数值所属的行全部删除，由于在MATLAB 中不能按照数值的大小直接将整理后的列中小于分层切平面高度值的数值所属的行直接删除，所以只能通过查找小于分层切平面高度值的数值所在矩阵中的行数中最大的那一行，然后将这一行以及行数小于这一行的行全部删除，经过这一过程后，将整个矩阵进行了精简。这一过程也就是将所有顶点在分层方向最大值小于该分层切平面的高度值的三角形面片剔除，达到了精简数据的目的。

(2)第三次排序和相交数据的提取

经过第二次的排序和数据的删除，已经将顶点在分层方向上的分量的最大值小于分层切平面的三角形剔除，经过删除后的矩阵只剩下与平面相交的三角形面片和最小值大于该分层切平面的三角形面片。

为了能够获得只与分层切平面相交的三角形面片，对删除后矩阵作第三次排序，然后将不与分层切平面相交的三角形面片排除，提取出只与分层切平面相交的三角形面片。这一过程中不能够对最小值大于分层切平面的三角形面片进行剔除，而只是用排除的方法，是为了提取只与分层切平面相交的三角形面片。而在(1)中的删除是对已不会再与其他分层切平面相交的三角形面片的彻底删除，达到数据精简的目的。经过本次过程能够把与该分层切平面相交的三角形面片全部提取出来。

三角形面片第三次排序在MATLAB 中实现方式:在第二次排序和数据删除后的矩阵中，找到三角形面片顶点坐标在分层方向分量最小值的那一列，将该矩阵的行按照这一列中的数值大小进行升序排列。经过第三次排序后，使得剩余三角形面片按照其顶点坐标在分层方向上的最小值的大小进行了有序的排列。

相交数据的提取在MATLAB 中实现方式:矩阵第三次排序完成后，将其排序列中数值大于分层切平面高度值的行全部排除，从该矩阵中的排序列里寻找到小于或者等于分层切平面的数值所在的最大行，然后从该矩阵中提取出这一行到最后一行，这部分矩阵中的数据就是与该分层切平面相交的所有三角形面片的数据信息。这一步主要是将顶点坐标在分层方向上的分量的最小值大于分层切平面高度值的三角形面片进行排除，然后把所有与分层切平面相交的三角形面片直接提取出来。

2.4 分层切平面与三角形面片的求交

通过对数据的排序，精简，提取出了只与分层切平面相交的三角形面片。对分层切平面与三角形面片的求交提出两种方法。(1)应用文献［8］中的Trioutline 函数直接获得分层切平面与三角形平面的交线段，然后采用边输出边制造的方法输出轮廓线;(2)对提取的三角形面片建立点表，求得切平面与其中一个三角形面片的两个交点后，按照顺序查找与其相邻的三角形面片，然后获得与其相邻的三角形面片另一个顶点，顺序求交直到切平面与初次相交的三角形面片再次相交时为止;这样求交，对每个三角形面片的每一个边只需求得一次交点，节省了对同一边两次求交所浪费的时间。

3 实例分析

快速成型技术要求分层算法要有较高的稳定性，而且在满足精度的前提下，能够很快地对模型进行分层运算，快速地输出快速成型机能够接受的分层轮廓线。

通过两个实例对该程序的快速性及稳定性进行验证。每一个例子都是以ASCII 的形式对STL 模型的进行读取。分层算法是在DELL N5010(处理器CPU:Intel(R)Core3)的Windows7 系统中安装的MATLAB R2010a 编程语言环境下运行的。

快速成型技术中，分层方向的不同，模型在制造精度、制作时间以及需要添加的支撑都会不同，那么对模型的成型效率和制作成本都会产生较大的影响。文中分别从z、y、x 3 个方向对两个模型进行分层处理试验，具体结果如下:

3.1 卡扣

该卡扣是由三维扫描点云经过转换得到的STL模型，该模型尺寸12.02 mm×29.00 mm×7.33 mm，面片个数50 329 个，顶点个数26 379 个，分层厚度为0.1 mm，3 个制作方向如图1所示。

图1 卡扣的分层图

3.2 斗齿

该斗齿模型也是由三维扫描点云转换得到的STL模型，尺寸为:97.64 mm ×222.00 mm ×89.69 mm，面片个数:101 462 个，顶点个数:50 727 个，由于该面片数据量较大，为了便于观察，将分层层厚设置为:3 mm，分别从z、y、x 3 个方向分层，如图2所示。

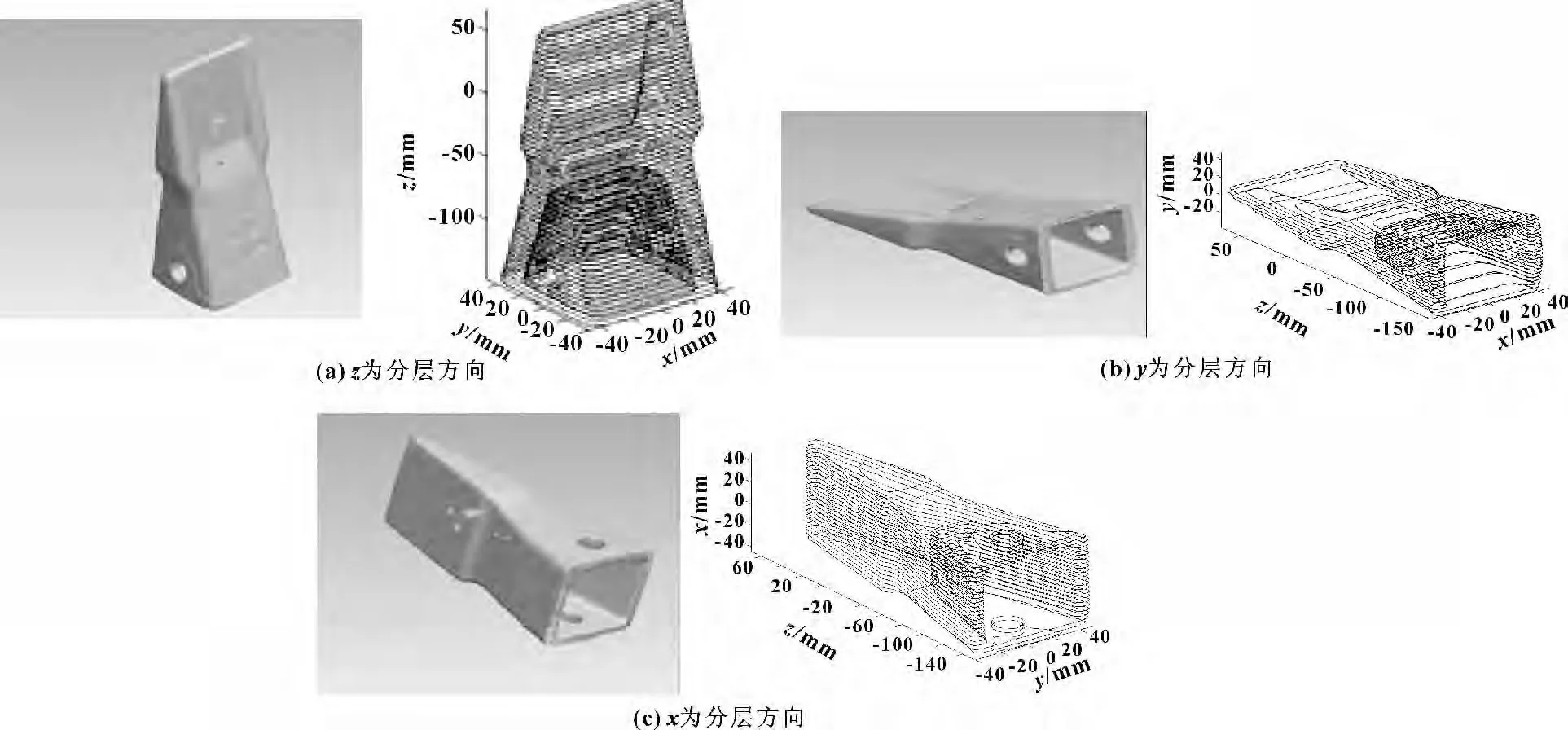
图2 斗齿的分层图

表1 文献［9］与文中算法相同精度对同一模型的分层对比

4 结束语

通过对STL 模型的排序、精简数据，直接提取只与分层切平面相交的三角形面片，然后快速输出截面轮廓线。通过实例显示该算法在保证精度的前提下，以较快的速度获得所需数据，在与文献［9］的对比中，文中算法不仅稳定性较高，而且速度较快，尤其在数据量较大的时候其运行速度明显快于文献［9］，是文献［9］运行速度的10 倍左右。

［1］PAN Haipeng，ZHOU Tianrui.Generation and Optimization of Slice Profile Data in Rapid Prototyping and Manufacturing［J］.Journal of Materials Processing Technology，2007，187/188:623－626.

［2］胡德洲，李占利，李涤尘，等.基于STL 模型几何特征分类快速分层处理算法研究［J］.西安交通大学学报，2000，34(1):37－40.

［3］牟小云，郑建明，田静云.基于坐标分层的STL 模型切片算法的研究［J］.机床与液压，2008，36(7):52－53.

［4］李仲阳，谢存禧，杨家红.基于STL 文件的快速成型分层算法与毗邻拓扑信息的快速提取［J］.计算机工程与应用，2002，4(7):3235－3236.

［5］赵吉宾，刘伟军.快速成型中基于STL 模型的分层算法研究［J］.应用基础与工程学报，2008，16(2):224－233.

［6］温佩芝，黄文明，吴成柯.一种改进的STL 文件快速分层算法［J］.计算机应用，2008，28(7):1766－1768.

［7］赵保军，汪苏，陈五一.STL 数据模型的快速切片算法［J］.北京航空航天大学学报，2004，30(4):329－333.

［8］马良，黄卫东.基于STL 数据模型动态拓扑重构的快速切片算法［J］.中国激光，2008，35(10):1623－1626.

［9］王春香，李振华.STL 模型分层算法的优化及应用［J］.机械设计与制造，2013(3):87－90.