基于SimMechanics的仿人机器人运动学仿真

江乐果，朱华炳

(合肥工业大学机械与汽车工程学院，安徽合肥230009)

0 前言

仿人机器人具有与人相似的步行运动方式，可以代替人类从事放射性、高强度、高危险性等有害环境下的工作［1］。仿人机器人与普通的工业机器人最大的区别在于步行状态、自由度数目较多、没有固定的基座，在对它进行设计与研究时，需要充分考虑步行的稳定性，逻辑合理性，因此针对仿人机器人的研究具有十分重要的意义。以下介绍的是基于Matlab/Sim-Mechanics 软件平台下所做的仿真分析。Matlab 软件运算功能强大，包含了很多可以用来解决实际工程问题的工具箱，其中SimMechanics 工具箱就可实现机械构件、关节、传感器、驱动器等组成部件的建模与仿真。针对普通的机械系统一般采用正向动力学分析和逆向动力学分析这两种分析方式，对于机器人机械系统可利用SimMechanics 工具箱提供的机构模块集来搭建仿真模型，这样显著地缩短了机械系统的分析时间，同时增加了可视化界面，可以更直观地观察机构的变化。

1 仿人机器人的动力学分析

对于机构的动力学分析常用的方法有拉格朗日法、牛顿－欧拉法、达朗贝尔法以及Kane 法等，以上几种方法基本上是等价的，只是每种方法的形式不同，在不同的领域各有应用［2］。Kane 方法较其他几种动力学分析有一些特点，它综合了分析力学和向量力学两方面的优点，着眼于广义速度、偏速度、偏角速度的确定，而且偏重于广义主动力、广义惯性力的计算，且步骤较程序化，方便计算机完成;避免了寻求系统以各种形式表示的动力学函数及它们的导数;Kane 方法不仅适用于完整系统也适用非完整系统。非完整系统的Kane 方程可由不考虑约束时系统的Kane 方程组合而成，这一结论使得机器手、步行机器人之类约束经常变动的动力学问题计算简化［3］。因此采用Kane 法对仿人机器人的机构模型进行动力学分析。

Kane 动力学方程可描述为:作用在系统上或刚体上相对于广义速率ur的广义主动力Fr和广义惯性力之和为0 ，即

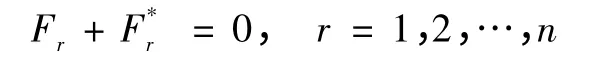
作用在质点j 上的力系和作用在刚体上的力矩系可简化到一固定点上，成为主力矢和主力矩。这样，可用把作用在刚体上的外力统一用Fj表示。同理，把刚体上的惯性力和惯性力矩统一用表示。广义主动力是外力Fj与第j 点的偏速度的点积，广义惯性力是惯性力与第j 点的偏速度的点积，即

求各质心点的偏速度和各刚体的偏角速度。将仿人机器人在运动过程中双脚支撑的瞬间，建立一个平面五杆机构运动模型，进行动力学分析，图1 为双脚支撑时的机构简图。以两条小腿杆即AB 杆、DE 杆的角位移φ1、φ4为独立变量，构成完整的多刚体系统，通过Kane 方程来描述系统。e1、e2、e3表示x、y、z 方向上的单位向量。

图1 双脚支撑机构简图

由Kane 方程广义速率

由机构封闭矢量图1 可得

对上式求导后可得，

同理得

同理可求得，

广义主动力F1和F2为

式中:F 为阻力;MA、ME为驱动力矩。

2 仿人机器人建模

2.1 机器人的基本外形尺寸

仿人机器人在设计时需要考虑的首要问题是组成机器人的各部分的尺寸比例需要符合人体的比例。图2 给出了人体各部分的尺寸相对于身高的比例图。这里仅作为仿人机器人外形尺寸的参考［4］。

图2 仿人机器人各个部位相对于身高的比例图(H 为人体身高)

根据人体的比例标准，假设人体身高是H，那么髋部关节距离足部为0.53H，其中，踝关节与足部距离是0.03H，大腿和小腿各为0.25H;人体肩部与足部的距离为0.83H，上臂的长度为0.18H，下臂的长度则为0.14H;头部的高度是0.13H，两肩膀之间的距离为0.23H，两髋部间距为0.2H。参照以上的尺寸比例，确定机器人的各个部位的基本外形尺寸，如表1所示。

表1 人体身高1 600 mm 时，各部位的外形尺寸

2.2 SimMechanics 仿真模型的建立

SimMechanics 主要应用于机械系统的刚体运动仿真，在SimMechanics 模块集中具有模拟旋转运动、平移运动、固定焊接等运动模块，可以方便地定义刚体的质量属性和运动属性。首先根据仿人机器人的身体结构，在SimMechanics 工具箱中选取需要的模块，然后按照刚体(body)—关节(Joint)—刚体—关节—刚体的方式组合在一起，形成一个完整的结构。最后添加上必要的驱动模块(Actuator)和传感模块(Sensor)，这样得到了机构的模型框图。依据机器人对称的结构，分为主躯体模型、头部模型、胳膊模型和腿足部模型。因为人类在行走过程中，两只脚轮流作为基座，人体的重心会发生一些变化，机器人真实的运动十分复杂。在此，以保持主躯体的重心稳定为前提，建立简化的仿真模型。

2.2.1 刚体质量属性的计算

在body 模块中，需要定义刚体的质量、惯量矩阵、位置参数。机器人的质量可以根据材料密度与体积的关系得到，位置参数由仿人机器人的基本外形尺寸得出。惯量矩阵属于刚体的重要参数，对于不规则的刚体形状，惯量矩阵的计算比较复杂，通常借助常见的三维绘图软件如Proe、Solidworks、UG 等得到，该仿人机器人经过简化后，构件形状规则，便于计算。

(1)细直杆的惯量矩阵

其中:细直杆在z 轴方向的长度为L。

(2)长方体的惯量矩阵

其中:a、b、c 分别为x、y、z 方向上的边长。

2.2.2 各部分模块框图

胳膊模型是由上臂与主躯体的转动副、上臂与下臂之间的转动副连接构成，模型框图见图3。

图3 胳膊模型框图

腿足部是一个比较复杂的模型结构，它是整体模型的重要组成部分，由它完成机器人的步行过程。腿部SimMechanics 模型图由3 个body 组成:大腿杆、小腿杆、足部，其中大腿与躯体通过旋转副连接，大小腿之间为旋转副连接，足部和小腿焊接在一起。另外，在大腿上增加一个电动机驱动，作为大腿向前运动的驱动力。人体的腿部是一个并联结构，以右腿为例，腿部模型见图4。

图4 腿部结构模型框图

仿人机器人整体模型由各个部分的结构模型图组成，而每个部分的模型图包含的模块比较多，为了使整体模型能够在Simlink 窗口界面显示出来，将其他各个部分创建成子系统，在以下的仿人机器人整体模型框图中，包含有头部模型子系统(Head)、左臂模型子系统(Left arm)、右臂模型子系统(Right arm)、左腿模型子系统(Left leg)、右腿模型子系统(Right leg)几个部分，图5 为仿人机器人整体模型框图。

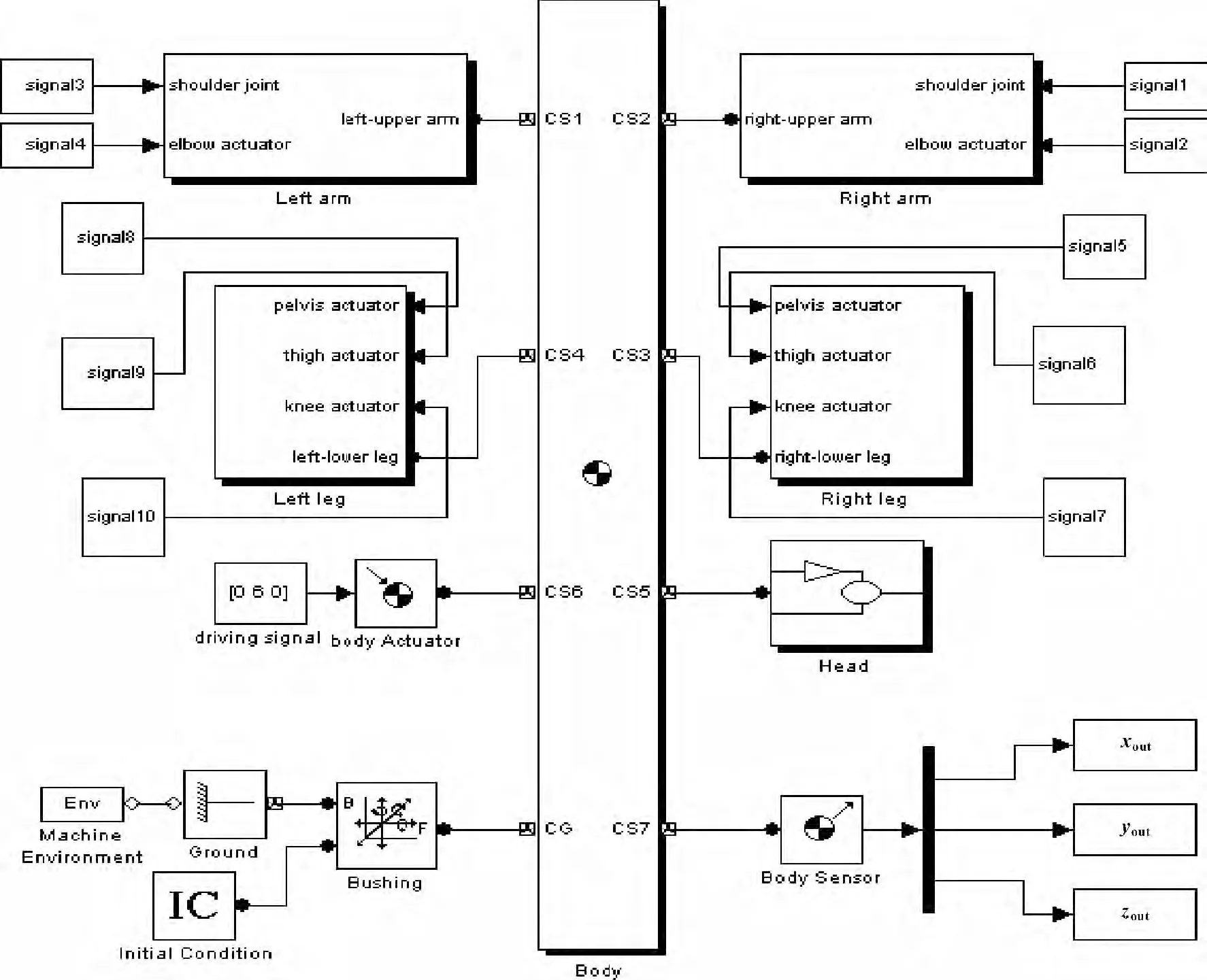
图5 仿人机器人整体模型框图

3 仿真结果及分析

按照图5 的整体模型图，给该机械系统输入60 s的运动时间，可以观察仿人机器人的运动变化过程，以及更加直观地显示出它在不同时刻的状态。在Simlink 工作界面的参数设置里，将更新与动画设置打开，在仿真中，会弹出仿人机器人的三维动画窗口。图6 为仿人机器人的三维动画图，图7 为仿人机器人的行走过程图，图中机器人是沿着y 轴方向前进。象。在10 s 和20 s 阶段，主躯体的重心与腿部保持了一致性，当行走了45 s 后发现重心前移，此时，机器人属于向前大步加速前进，这基本符合了人体行走的过程。

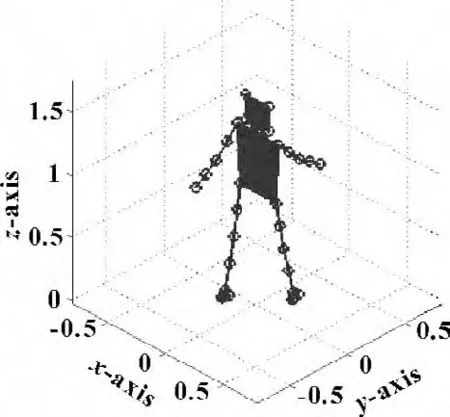
图6 仿人机器人的三维动画图

图7 仿人机器人行走过程

图8 仿人机器人不同时刻的状态图(侧视)

根据图8 机器人在不同时刻的状态，可以得出:在给定机器人合适的驱动力和控制函数，就能够保证机器人在步行过程中的稳定性，避免身体发生倾覆现

在SimMechanics 机器人的整体框图中，通过to workspace 模块将躯体重心的变化输入到Matlab 主界面中，调用Figure 窗口，可以清晰地描绘出主躯体重心的角加速度在3 个方向上的曲线变化图，见图9。图中曲线变化表明，仿人机器人在行走过程中，角加速度在z 轴方向改变量微小，随着左右腿的轮流作为支撑腿，重心在x 轴反向得到一个波动图，y 方向上的变化值也很小。

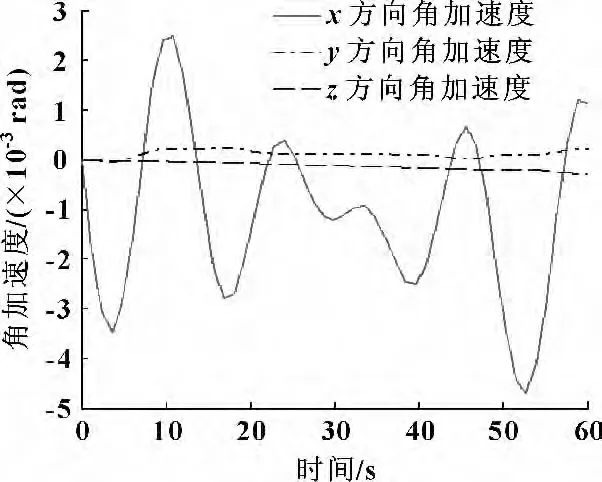
图9 仿人机器人躯体重心的角加速度

机器人的支腿模型图中，将足部与小腿焊接在一起，在足部刚体模块上添加了位移传感器，将数据传入工作界面中，得到图10。由图10 可知，机器人在y 方向上并非匀速运动，速度在逐渐增加。使机器人保持匀速前进，是接下来研究的一个重点内容。

图10 仿人机器人足部速度

机器人的转向是通过上身与腿部之间的髋部来实现的，髋部在以z 轴的旋转中承受着扭矩的作用，文中仿人机器人是实现直线行走，在腿部的摆动中，髋部并不是作纯摆动，为了使机器人沿y 方向直线前进，因此它的髋部需承受几个方向上的反扭矩作用，从而保持行进的准确性和稳定性。图11 为机器人在给定的时间内髋部所承受的扭矩大小。

图11 仿人机器人髋部的计算扭矩及各方向上的反扭矩

4 结论

仿真实验结果表明，对于预定的输入信号，仿人机器人的末端执行器能够按照预期的方式进行平稳连续的运动。各关节的力矩和速度都在工作范围内，足部对地面的接触也属于柔性冲击，主躯体的重心变化平稳，整个运动过程连贯，达到了仿真要求。通过仿真实验可以看出，在机械系统的设计及仿真优化过程中，Matlab/SimMechanics 软件相比普通的数值计算方法有很大的优势。在接下来的研究中，将根据更加精确的人体步态轨迹，推导验证出控制机器人各部位运动的驱动函数，最后得到最优化的仿人机器人运动仿真结果。

［1］刘成军，薛方正，李祖枢，等.双足机器人动态步行仿人智能控制［J］.重庆大学学报，2013，36(2):45－50.

［2］王树新，姜文兰，刘又午.多臂机器人系统的动力学分析与实验［J］.天津大学学报，1996，29(4):533－537.

［3］苏曙.Kane 方法及其特点［J］.机械设计，1993，(4Z):4－6.

［4］朱秋国.仿人机器人结构设计与分析［D］.杭州:浙江大学，2011.

［5］张晓超，董玉红.基于MATLAB/Simulink 的机器人运动学仿真［J］.现代制造工程，2005(S1):66－67.

［6］宫赤坤，高丽丽.仿人机器人的设计与实现［J］.机械传动，2013，37(5):43－49.

［7］李颖，朱伯立，张威.Simulink 动态系统建模与仿真基础［M］.西安:西安电子科技大学出版社，2004.

［8］杨东超，刘莉，徐凯，等.拟人机器人运动学分析［J］.机械工程学报，2003，39(9):70－74.

［9］伊强，付成龙，陈恳.基于Simulink 的仿人机器人步行运动仿真模型［J］.机械设计与制造，2010(12):1－3.

［10］王鲁敏，李艳文.基于Matlab 的教学型机器人空间运动轨迹仿真［J］.机械与电子，2005(9):55－58.