一种基于多普勒频率变化率单站无源定位的改进跟踪滤波算法

谈欣荣，高宪军，李宝珠，王 宇

（1.空军航空大学 研究生队，吉林 长春 130022；2.空军航空大学 科研部，吉林 长春 130022；3.空军航空大学 军事仿真技术研究所，吉林 长春 130022）

无源定位技术是一种定位设备本身并不主动发射信号，而仅仅依靠被动接收辐射源的信息来实现定位的技术[1]。单站无源定位主要有两个方面的难点：一是相对较少的测量信息使得单一时刻的测量信息无法实现对目标辐射源的相对定位；二是目标辐射源复杂的运动形式使得精确的跟踪方程难以建立，从而影响跟踪算法的精度。针对上述困难，本文选择了基于多普勒频率变化率的无源定位方法进行定位。但是光靠单站无源定位技术还不足以获取运动目标连续的位置信息，需要进行有效的跟踪滤波。

在机动目标跟踪领域，交互式多模型（IMM）算法[2-3]被认为是迄今为止最有效的算法之一。交互式多模型算法考虑了模型的特点，它假设目标有多种运动状态，每一种运动状态对应一种模型，目标在任意时刻的运动状态都可以用给定模型中的一种来表示，而运动状态的变化也就是运动模型之间的切换用齐次马尔可夫链表示，目标的滤波结果是多个模型滤波结果的加权综合。对于不同的应用要求，IMM算法又可能结合多种滤波算法。将IMM算法与卡尔曼滤波器（Kalman Filter，KF）或者无迹卡尔曼滤波器（Unscented Kalman Filter，UKF）结合，这样做有算法简单，计算量小等优点，但是这些算法存在线性化误差，估计精度不高，且不适用于非高斯问题。将IMM算法与粒子滤波相结合的IMM-PF算法（Interacting Multiple Model Particle Filter）[4-9]集成了IMM对机动目标的跟踪的良好特性，同时避免了线性化误差和高斯噪声的限制，有效的提高了状态估计的精确度。但粒子滤波的主要问题是计算量大，若多模型中的每个模型匹配一个粒子滤波器，计算量无疑会很大，影响跟踪的实时性。

针对以上问题，本文提出了一种改进的IMM滤波算法（IMMKF-UKF-PF）进行定位跟踪。其原理是：将系统的多模型分成三类，一类是线性模型，匹配卡尔曼滤波；一类是三阶及三阶以下非线性高斯模型，匹配无迹卡尔曼滤波；一类是三阶以上非线性高斯模型或非高斯模型，匹配粒子滤波。仿真结果表明该算法大大改善了计算效率。

1 利用多普勒频率变化率的二维单站无源定位原理

如图 1 所示，观测平台在位置（xo，yo）处以（x˙o，y˙o）作直线运动，目标辐射源在位置（xT，yT）处以（x˙T，y˙T）作直线运动，二者之间的相对位置（x，y）=（xT-xO，yT-yO）。

图1 二维平面观测平台与目标辐射源几何示意图Fig.1 Observation platform and target in the two-dimensional

根据几何关系和运动学原理，经过一系列推导得观测站平台和辐射源之间的距离为

然后根据三角原理得出目标辐射源的位置（xT，yT）:

在多次测量的情况下，选择适当的非线性跟踪滤波算法，对辐射源进行跟踪定位。

2 IMMKF-UKF-PF滤波算法

设一个使用确定模型集合 M={Mi|i=1，2，…，M}的混合系统，状态方程和观测方程离散形式为：

其中 xi（k）表示在模型 i（i=1，2，…，M）下的目标运动状态矢量，vi是相应的非高斯过程噪声，zi（k）是观测矢量，r是高斯观测噪声。Qi（k）和 R 分别是 vi（k）和 r（k）的协方差。一共有 M 个模型，假设其中1到M1是线性的，M1到M2时是三阶及三阶以下非线性高斯模型，其它是三阶以上非线性高斯模型或非高斯模型。

系统模型之间的转移概率用一个马尔可夫链来表示：

图2给出了IMMKF-UKF-PF滤波算法结构示意图，从k-1时刻开始到k时刻，一个采样周期的IMMK-UKF-PF实现步骤如下：

步骤1：输入交互

图2 IMMKF-UKF-PF滤波算法结构示意图Fig.2 Filter algorithm structure of IMMKF-UKF-PF

步骤2：滤波

在交互运算的结果和观测量z（k）的基础上，通过 3种滤波器，得到各模型的状态估计量xˆi（k|k）和协方差估计量Pˆi（k|k）。由于进行滤波算法时与常规的IMM-KF、IMM-UKF算法和IMM-PF算法近似，这里不再赘述。

步骤3：模型概率更新

各模型概率更新如下：

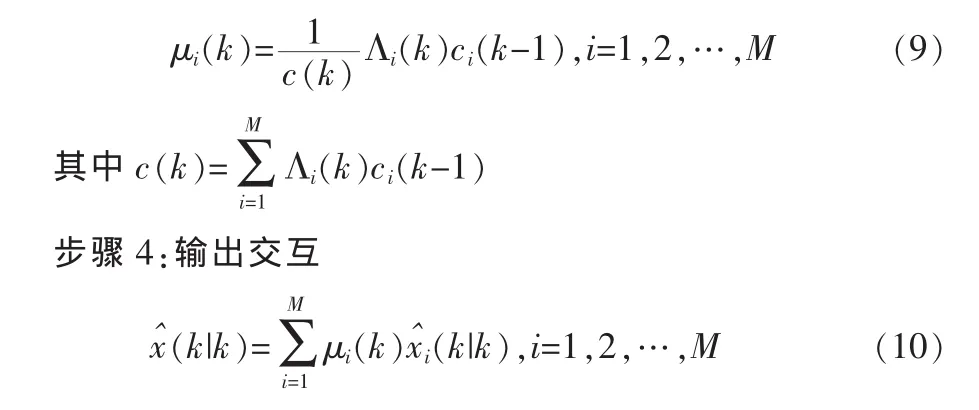
3 数学建模及仿真验证

为了验证本文改进的IMM算法的有效性，将其与IMM-UKF、IMM-PF算法进行Matlab仿真，并将仿真结果进行比较分析。

仿真中采用CV模型、CA模型和JERK模型[10]进行交互。

当目标处于匀速运动时，用xi=xTi-xOi、yi=yTi-yOi表示目标的相对位置，用表示目标与观测站相对速度，选取状态变量建立如下状态方程：

建立如下状态方程：

当目标处于变加速运动时：X或Y一维情况下状态转移矩阵为

式 中 p1=（2-2αT+α2T2-2e-αT）/2a3，q1=（e-αT-1+αT）/α2，r1=（1-e-αT）/α，s1=e-αT，参数 α 为“机动”频率。

观测方程

下标 m 表示为含有噪声的观测量， 其中 vβ、vβ˙、 vf˙分别为相互独立服从零均值高斯分布的测量误差。

假设测量条件为：观察间隔为T=1 s，波达角、波达角变化率和频率变化率的测量精度分别取：5×10-3rad、0.2×10-3rad/s、1 Hz/s。各模型滤波状态初始化，假定目标距离搜索范围为0～500 km，目标速度范围假定为-500～500m/s，且初始分布假定为均匀分布，在此假定下可由概率论知识得到目标位置和速度的期望值以及相应协方差值。 X（0）=[8 000，50，7 000，60]T是初始状态矢量，P=diag（1，1，1，1）是初始状态协方差，各模型初始概率均为1/3，模型转移概率矩阵为

粒子滤波时模型的粒子数为N=800，蒙特卡罗仿真次数为100。

仿真结果如图3、4、5所示，分别表示IMM-UKF、IMMPF、IMMKF-UKF-PF 3种算法估计目标位置的误差曲线。

图3 X方向均方根误差Fig.3 Error of X direction

图4 Y方向均方根误差Fig.4 Error of Y direction

图5 R方向均方根误差Fig.5 Error of R direction

Execution time （seconds）

TIMM-UKF=5.451 2，TIMM-PF=13.451 2，TIMMKF-UKF-PF=6.032 4

由图3、4、5以及仿真时间可以得出，IMMKF-UKF-PF滤波算法的均方根误差略小于IMM-PF算法，跟踪性能有一定的改善，IMM-UKF算法跟踪性能最不理想；最重要的是IMMKF-UKF-PF滤波算法仿真所用时间相比IMM-PF减少很多，与IMM-UKF相近，这在现实应用中具有重要的意义。

4 结束语

本文在基于多普勒频率变化率的单站无源定位问题的基础上提出了一种改进的交互式多模型滤波算法 （IMMKFUKF-PF），利用不同的模型匹配不同类型的滤波器，IMMKFUKF-PF算法充分发挥了粒子滤波和无迹卡尔曼滤波以及卡尔曼滤波各自的优点，大大地提高了计算效率，减少了跟踪定位所用时间，同时该算法具有良好的跟踪性能和较强的鲁棒性。在实际的机动目标跟踪中，目标的运动情况比较复杂，往往需要多个不同参数的线性及非线性模型进行匹配，在这种情况下，采用IMMKF-UKF-PF算法改善的计算负荷是可观的。

[1]华铁洲.单站无源定位关键技术研究和误差分析[D].河南:信息工程大学信息工程学院，2010.

[2]杨丽娜，袁铸.CS模型下的IMM算法在目标跟踪中的应用[J].计算机工程与应用，2010，46（33）:230-232.YANG Li-na，YUAN Zhu.Application of IMM algorithm based onmodelCS in target tracking[J].Computer Engineering and Applications，2010，46（33）:230-232.

[3]宫淑丽，王帮峰，吴红兰，等.基于IMM算法的机场场面运动目标跟踪[J].系统工程与电子技术，2011，33（10）:2322-2326.GONG Shu-li，WANG Bang-feng，WU Hong-lan.Tracking of moving targets on airport surface based on IMM algorithm[J].SystemsEngineeringand Electronics，2011，33（10）:2322-2326.

[4]刘长江，王超锋，宋春林.基于时差及多普勒频差的IMM无源定位算法[J].现代雷达，2011，33（5）:36-38.LIU Chang-jiang，WANG Chao-feng，SONG Chun-lin.IMM algorithm for passive location based on TDOA and FDOA[J].Modern Radar，2011，33（5）:36-38.

[5]华铁洲，李冬海，陈剑宇.一种改进的单站无源定位算法[J].电子对抗，2010（2）:11-14.HUA Tie-zhou，LI Dong-hai，CHEN Jian-yu.An improved single observer passive location algorithm[J].Electronic Countermeasures，2010（2）:11-14.

[6]王喜鹏，王飞.机载无源定位精度分析[J].舰船电子对抗，2012，35（3）:24-26.WANG Xi-peng，WANG Fei.Analysis of airborne passive location precision[J].Shipboard Electronic Countermeasure，2012，35（3）:24-26.

[7]杨晓君，陆芳.模糊单站无源定位方法[J].清华大学学报，2011，51（1）:25-29.YANG Xiao-jun，LU Fang.Obscure method of single observer passive location[J].Journal of Tsinghua University，2011，51（1）:25-29.

[8]Boers Y，Driessen J N.Interacting multiple model particle filter[J].IEE Proc.-Radar Sonar Navig，2003，150（5）:344-349.

[9]BLOM H A P，Bloem E A.Particle Filtering for Stochastic Hybrid Systems[C]//43 IEEE Conference on Decision and Control，2004.USA:IEEE，2004，3:3221-3226.

[10]杨翠芳，汪圣利，周丰.基于参数自适应Jerk模型的IMMUKF算法[J].自动化技术与应用，2010，29（1）:47-52.YANG Cui-fang，WANG Sheng-li，ZHOU Feng.Interacting multipie model UKF algorithm based on jerk model with adaptive parameter[J].Techniques of Automation and Applications，2010，29（1）:47-52.