基于EEMD算法在信号去噪中的应用

周先春，嵇亚婷

（南京信息工程大学 电子与信息工程学院，江苏 南京 210044）

语音去噪技术是语音信号处理领域的一个重要的研究方向，它在改进语音质量、提高语音清晰度、解决噪声污染等方面有着至关重要的作用。尽管目前有小波分析的方法[1]可以有效的改进信号分析方法存在的不足，但是用小波分析方法任然存在选择匹配小波基的困难，所以很难根据语音信号的特点自适应的调整小波基。

经验模态分解（Empirical Mode Decomposition，简称EMD）是今年来发展起来的一种适用于处理非线性、非平稳信号的分析方法，由于EMD分解存在端点效应和模态混叠现象，针对这一问题，通过一种白噪声辅助数据分析方法——集合经验模态分解 （Ensemble Empirical Mode Decomposition，简称 EEMD），可以部分解决端点效应和模态混叠现象，本文为更有效的解决EMD所存在的问题。

1 小波阈值去噪方法

基本思路[2-3]:

1）计算含有噪声信号的正交小波变换。

2）对分解得到的小波系数进行阈值处理。

3）进行小波逆变换。

2 EMD算法

2.1 IMF的性质

EMD算法的基本实现过程是用筛选的方法把一个复杂的信号分解为有限个固有模态函数（Intrinsic Mode Function，简称IMF）之和，这里IMF必须满足以下两个性质：

1）信号的极值点（极大值或极小值）数目和过零点数目相等或最多相差一个。

2）由局部极大值构成的上包络线和由局部极小值构成的下包络线的平均值为零。

2.2 EMD算法的计算步骤

1）计算出信号 s（t）所有的局部极值点。

2）求所有的极大值点和极小值点构成的上下包络线，分别记作 u0（t）和 v0（t）。

同时记信号上、下包络线的均值的差为 h0（t）=s（t）-m0（t）。

4）判断 h0（t）是否满足 IMF 的两个性质。 若满足，则 h0（t）是 IMF；否则，记 h0（t）为 s（t）重复步骤 1）～3），直到得到第一个 IMF，记为 c1（t）。

5）记 r1（t）=s（t）-c1（t）为新的待分析信号重复步骤 1）～4），以得到第二个 IMF。 记为 c2（t），此时余项 r2（t）=r1（t）c1（t）。重复上述步骤，直到得到的余项rn（t）是一个单调信号或rn（t）的值小于预先给定的阈值，则分解结束。

最终可以得到 n 个 IMFs，即 c1（t），c2（t），…，cn（t）余项为rn（t），因此，原始信号 s（t）可以表示为

3 EEMD算法和端点效应以及模态混叠现象

3.1 EEMD算法原理

EEMD[5]是针对EMD方法的不足,提出了一种噪声辅助数据分析方法。EEMD的本质是在原始信号中叠加高斯白噪声后进行多次的EMD分解，利用高斯白噪声在多次试验叠加的情况下能够相互抵消，而原始信号中真正有用的信号在多次加入白噪声的试验后作为均值保留下来。

集合经验模态分解方法的核心是经验模态分解，原始信号加入随机白噪声后分解，得到了从高频到低频有序排列的多阶IMF分量，其本质上是一个从高频到低频不断滤波的过程，体现了多分辨分析自适应的滤波特性。

EEMD算法的分解流程图如图1所示。

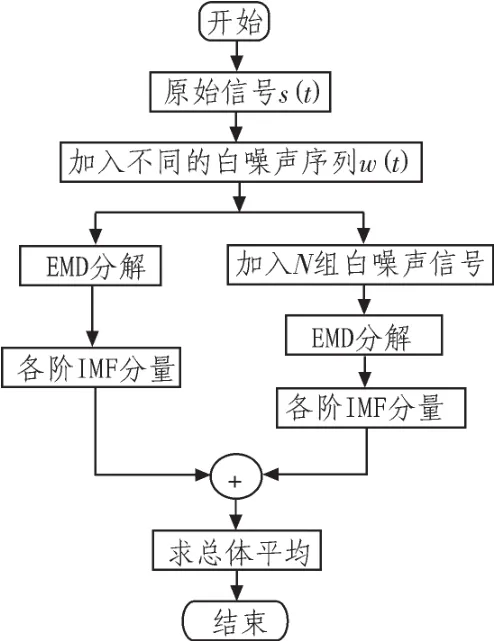
图1 EEMD算法的分解流程图Fig.1 Decomposition flowchart of EEMD algorithm

EEMD算法是在EMD算法的基础上，加入白噪声用以对原信号进行分解，主要基于统计学中对某个被分析量通过多次测量求平均值做为真值。在原始信号s（t）中加入不同的白噪声序列 w（t）后得到一个复合信号 S（t）；对复合信号 S（t）进行EMD分解，得到各阶 IMF分量，此时其中 ck（t）为各阶 IMF 分量，rin（t）为余项；若得到的各阶 IMF分量不满足IMF的两个性质，则在复合信号中加N组白噪声信号并进行EMD分解，得到各阶IMF分量，此时,其中为各阶IMF分量，为余项；利用高斯白噪声频谱的零均值原理，消除高斯白噪声作为时域分布参考结构带来的影响，原始信号对应的 IMF 分量 cn（t）可以表示为最后，原始信号 s（t）可以分解为其中 cn（t）为各阶IMF 分量，rm（t）为余项。

3.2 EEMD算法的端点效应和模态混叠现象

EMD和EEMD算法中的极值点是不能确定的，所以使得从第一个IMF分量开始就出现一定的误差，最终从端点处开始逐渐放大，产生虚假的IMF分量，这就造成了端点效应。

而出现模态混叠现象是因为信号中的某个频段的分量不连续所造成的所以在进行EMD分解前加入白噪声，这就保证了信号的每一个固有模态函数在时域上的连续性。最后利用白噪声是均值为零随机过程的特性，对EMD分解得到的各个IMF分量求均值，用以消除信号加入白噪声的影响。

4 仿真以及结果分析

4.1 随机噪声滤波

本文通过一个正弦信号，针对随机噪声和高频连续噪声进行滤波分析。含随机噪声信号的仿真如图2所示，原始信号是一个正弦信号，叠加一个随机信号，分别用改进后的EEMD方法与小波阈值去噪方法对含随机噪声的信号进行去噪[6]。

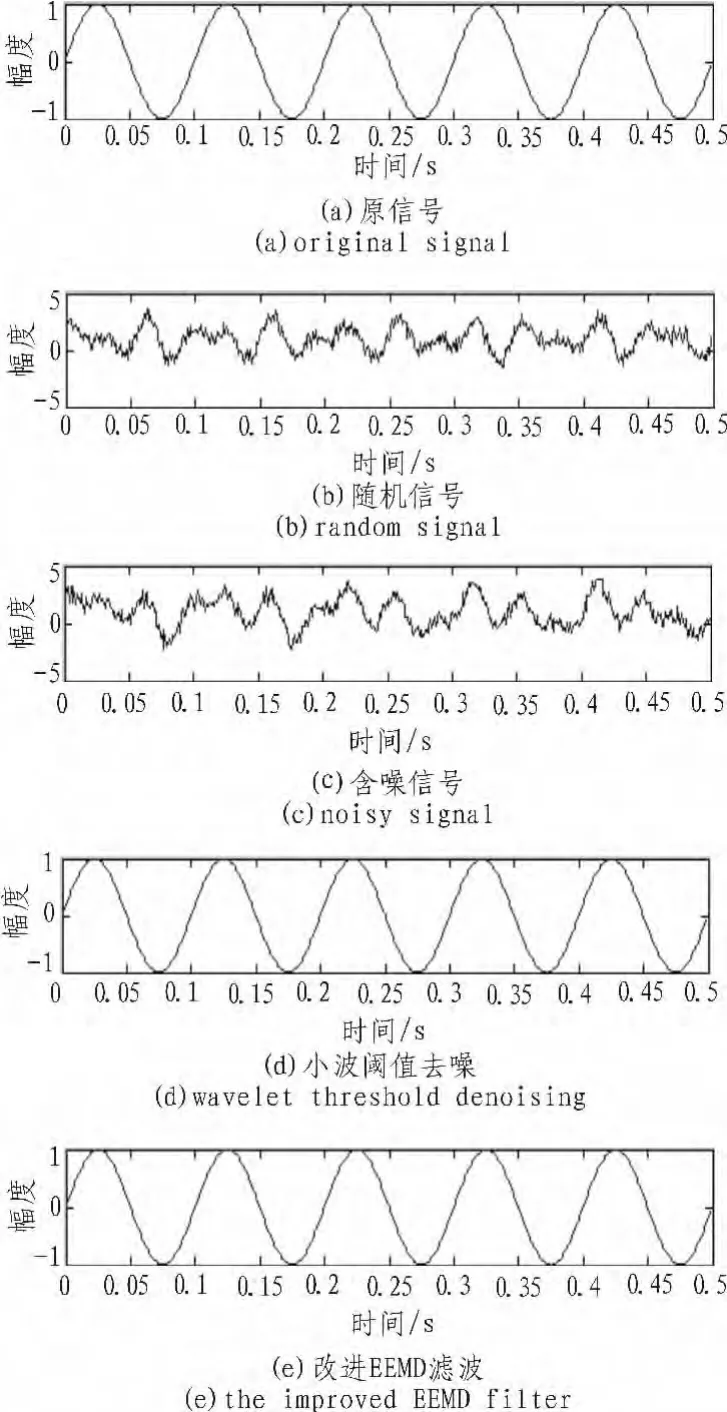
图2 仿真结果图Fig.2 Simulation results

4.2 高频连续噪声滤波

含高频连续噪声信号的仿真如图3所示，原始信号是一个正弦信号，加入一个连续干扰的白噪声信号，分别采用改进的EEMD方法和小波阈值去噪方法对含有高频连续噪声信号进行去噪。

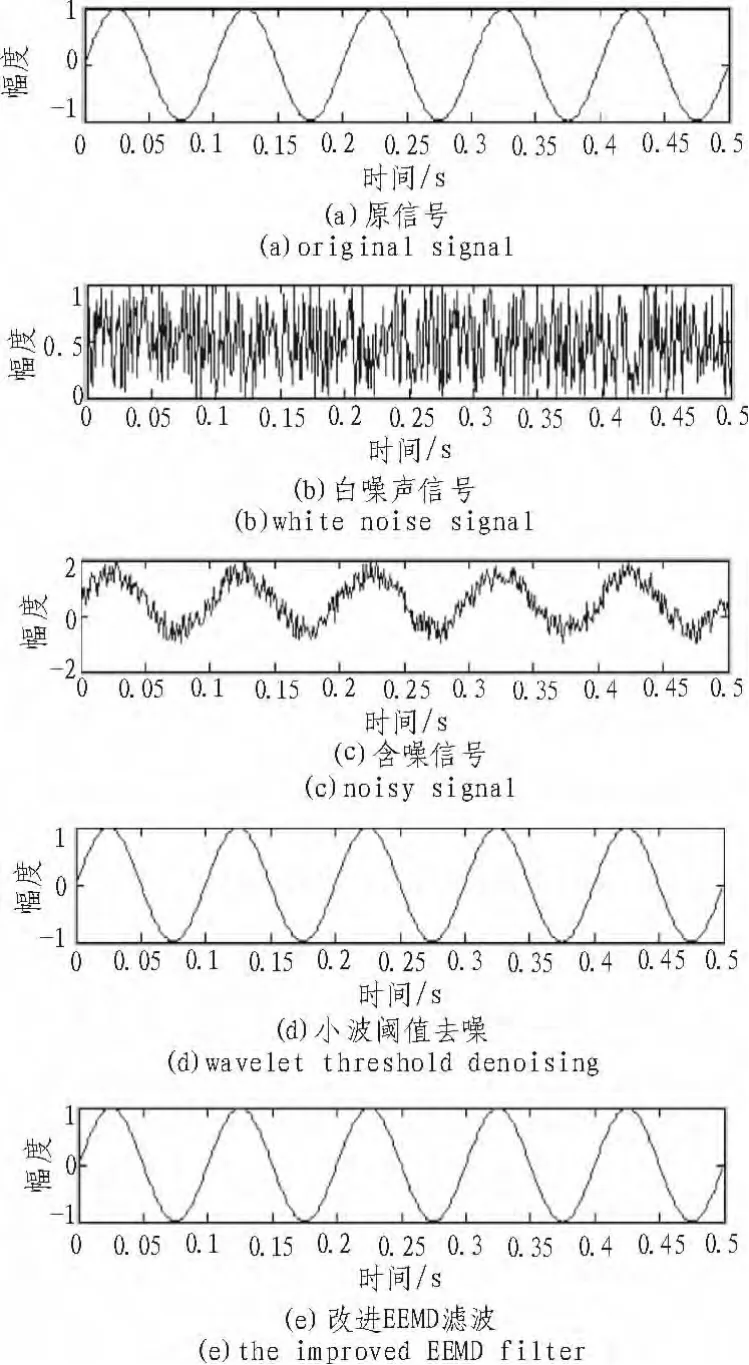
图3 仿真结果图Fig.3 Simulation results

4.3 结果分析

1）可以看出，改进后的EEMD方法有效的抑制了原始信号中因信号中某个频段不连续所产生的模态混叠现象，提高了信号的纯净度。

2）实验表明，无论是改进后的EEMD方法还是小波阈值去噪方法都有很好的滤波效果。去噪后信号的波形较为光滑，不存在太大的波动，较好的还原了原始信号。

3）运用小波阈值去噪方法时，不仅要考虑不同小波基滤波的特性不同，同时还要考虑分解层数、阈值选取等问题，而基于EEMD滤波器组的滤波方法就不需要考虑这些问题，因为它是一种自适应滤波的方法。

4）虽然基于EEMD滤波器组滤波的方法和小波阈值去噪方法都能很好的对含噪信号进行去噪处理，但是，从仿真结果可以看出，基于EEMD滤波器组滤波的方法比小波阈值去噪方法更能有效对原信号进行去噪处理，得到的信号更为光滑。

5 结 论

本文在EMD算法的基础上，提出了一种改进的语音去噪算法，即 EEMD算法，利用MATLAB平台验证了EEMD算法去噪的可行性，并与小波阈值去噪方法进行比对，实验表明，EEMD算法很好的解决了EMD算法在分解过程中出现的端点效应和模态混叠的现象，比小波阈值去噪方法更能很好的还原原始信号。

EEMD分解可以从数据中自适应的得到基函数，不需要先验的知识，就可以有效的滤除信号中的噪声信号。最后通过仿真可以看出，EEMD算法确实能够有效的去除信号中的噪声信号，同时与小波阈值去噪方法进行对比，进一步说明了该改进方法的有效性。

[1]Zhang F.Method of the speech signal denoising and purification based on wavelet transform [J].Electronic Measurement Technology，2009，32：68-71.

[2]LIShi-xin，ZHANG Xing-hui，WANG Jian-ming.A new local adaptive wavelet image de-noisingmethod[J].IEEE Computer Society，2011：154-156.

[3]李克粉，王直.改进的小波阈值去噪在语音识别中的应用[J].计算机技术与发展，2013，23（5）:231-234.LI Ke-fen，WANG Zhi.Improved wavelet thresholding in speech recognition applications[J].Computer Technology and Development，2013，23（5）:231-234.

[4]赵雯雯，曾兴雯.一种新的EMD去噪方法[J].电子科技，2008，21（5）:30-33.ZHAO Wen-wen，ZENG Xing-wen.A new signal denoising method based on empirical mode decomposition[J].Electronics Technology，2008，21（5）:30-33.

[5]WU Zhao-hua，HUANG Norden E.Ensemble empiricalmode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis，2009，1（1）:1-41.

[6]刘海波，赵宇凌.集合经验模态分解的稳健滤波方法研究[J].振动与冲击，2013，32（8）:63-67.LIU Hai-bo，ZHAO Yu-ling.Studies on robust filtering method of collection of empirical mode decomposition[J].Vibration and Shock，2013，32（8）:63-67.