多级加筋板结构承载性能与缺陷敏感度研究①

王 博，田 阔，郝 鹏，杜凯繁，周 演， 蒋亮亮，骆洪志，陈友伟

(1.大连理工大学 工程力学系,工业装备结构分析国家重点实验室，大连 116024； 2.北京宇航系统工程研究所，北京 100076)

0 引言

加筋板作为一种典型的薄壁结构形式，具有较高的比强度和比刚度，广泛应用于运载火箭的燃料贮箱[1]、导弹的级间段[2]等。提高加筋板在轴压工况下的极限承载性能,已成为载人航天与探月工程任务工程设计的目标。近年来学者们开展了系列工作：Bushnell[3]发现当加筋板具有不同高度的加筋时会提高结构的线性局部屈曲载荷值。在此基础上，Watson[4]考虑了加筋板的后屈曲能力，并基于VICONOPT软件对加筋板的筋高进行了优化设计。Murphy[5]、Quinn等[6-7]采用数值分析与实验相结合的手段，验证了在初始筋条间引入细密的子筋(Substiffener)可有效改善结构抗局部屈曲效果，进而提高结构极限承载能力。

为提高加筋板结构的极限承载能力，梁东平[8]、荣晓敏[9]等针对完美加筋板结构开展了相关的结构优化设计工作。Paulo[10]、郝鹏[11]等指出，忽略缺陷影响，一味追求结构减重和承载力最大所获得的最优设计往往表现为对缺陷非常敏感。而实际工程中缺陷是不可避免的，因此基于缺陷敏感度的承载力评估具有重要意义。王博[12]、郝鹏[11]曾基于数值分析手段，考察了加筋柱壳对单点凹陷缺陷和模态缺陷的缺陷敏感度。Hao和Wang[13]还在考虑后屈曲极限承载能力的前提下，发展了基于名义承载力指标的加筋筒壳结构最优设计方法，有效获得不同类型初始缺陷下的加筋筒壳结构的最优设计。此外，Rigo[14]、Lynch[15]和Yoon[16]等也研究了不同形状和幅值的缺陷对传统单级加筋板极限承载能力的影响。调研文献表明，通过加筋构型改变，提高结构抗缺陷能力的研究工作并不多见，其中Quinn[6-7]等实测了一种多级加筋板的几何缺陷并进行实验分析。因此本文将围绕多级加筋板结构，基于数值分析开展相应的承载性能与缺陷敏感度分析研究工作。

本文首先针对轴压工况下相同质量的单级与多级加筋板进行极限承载力分析，从多级加筋板失稳趋于局部化的角度阐释了其具有较高承载性能的力学机理；进而分析了筋高比对完美多级加筋板极限承载能力的影响；文中以单点凹陷缺陷为例，对单级与多级加筋板开展了缺陷敏感度分析，考察了单点凹陷缺陷的幅值与位置的影响；最后分析了筋高比对含缺陷的多级加筋板极限承载能力的影响。

1 多级加筋板极限承载能力分析

1.1 多级加筋板模型描述

本文对多级加筋板性能的研究均以等质量的传统单级加筋板作为对比。传统的单级加筋板结构示意图如图1(a)、(b)所示。加筋板蒙皮长度Lm=480 mm，宽度bm=360 mm，厚度tm=2 mm。共有9根加筋条，其高度hr=12 mm，厚度tr=4 mm，筋条间的间距br1=40 mm，蒙皮侧边与邻近的筋条距离br2=20 mm。本文提出的新型多级加筋板结构在不改变原有单级加筋板的结构布局与整体质量的条件下，仅对筋条高度进行调整，其中大筋高hl=20 mm，大筋厚tl=4 mm，小筋高hs=8 mm，小筋厚ts=4 mm，结构形式如图1(c)、(d)所示。模型材料选用2024号铝合金，是国内飞机、导弹与运载火箭结构中承力结构常用的铝合金牌号。其弹性模量E=72 000 MPa，泊松比ν=0.31，密度ρ=2.8×10-6kg/mm3，屈服强度363 MPa，强度极限463 MPa，延伸率12%。

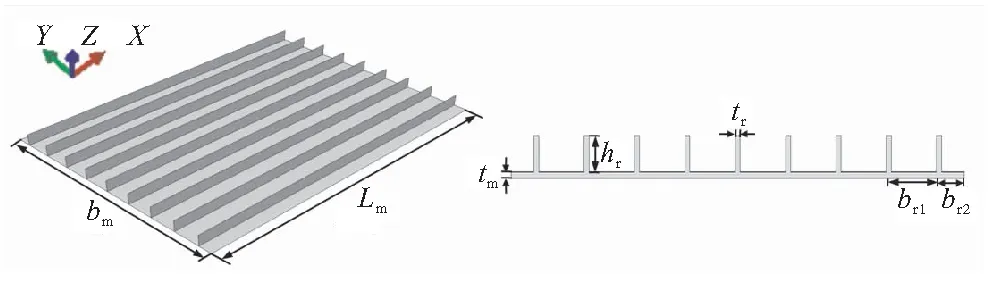
(a)传统单级加筋板 (b)传统单级加筋板剖面

(c)多级加筋板 (d)多级加筋板剖面

1.2 多级加筋板极限承载力分析

对于加筋板结构，显式动力学方法的准静态求解技术可准确模拟结构后屈曲行为，并能相对较快地得到结构极限承载力，且该方法稳健、不存在收敛性问题[17-18]。因而，本文基于商用有限元软件ABAQUS的显式动力学方法开展结构极限承载性能与缺陷敏感度评估。为模拟出准静态加载，需对模型加载时间进行依赖性分析，确定显式动力学分析的加载时间取为200 ms，加载总位移为2 mm。采用四节点壳体减缩积分单元S4R对加筋板模型进行离散，并进行单元依赖性分析确定最终的单元尺寸为5 mm。模型侧边自由，底端固支，顶端约束除轴向位移外的其余自由度，并将顶端面所有节点刚性耦合至参考点，在参考点上施加轴压位移载荷直至结构发生失稳破坏。

通过显式动力学分析，图2给出了单级与多级加筋板的位移-载荷曲线及其失稳时的变形云图，其中单级加筋板与多级加筋板极限承载值分别为165.9 kN和181.4 kN，在质量和加筋布局相同的条件下多级加筋板的极限承载力相较于单级加筋板提高了9.3%。通过对比加筋板失稳过程的变形云图可发现，单级加筋板在y向上均布单一尺寸的加筋，因而y-z向抗弯刚度分布呈现单一、相对均匀的周期性变化，这导致在x方向受压的情况下，结构局部失稳波形将快速扩展，易引发总体屈曲变形进而导致结构整体失效，表现出结构整体刚度迅速地折减；而多级加筋板由于刚度分布不均，容易将结构失稳变形抑制在大筋之间的局部区域内，而小筋实现了薄蒙皮的局部加强，由于大筋抗弯刚度较大，整体失稳波形被大筋间隔，呈现出“失稳局部化”，这种难以扩展的失稳现象，对保持结构x方向的极限承载力非常有利。

图2 传统单级与多级加筋板位移-载荷曲线

2 筋高比对完美多级加筋板极限承载能力的影响

对多级加筋板而言，大筋与小筋的“筋高比”反映了加筋板的y-z方向局部抗弯刚度分配与x方向抗压刚度分配情况，其对加筋板的承载力存在较大影响。前一章给出的多级加筋板模型的大筋高度hl=20 mm，小筋高度hs=8 mm，筋高比hl/hs=2.5。而单级加筋板可理解为筋高比hl/hs=1.0的多级加筋板。为讨论筋高比的变化对于多级加筋板承载力的影响，本章保持结构质量及筋条厚度不变，仅改变筋高比，使其在1.0～10.0范围内变化。图3绘制出结构极限承载力关于筋高比变化的曲线图。

由图3可明显看出，由于加筋板筋高比的变化，导致加筋板呈现出不同的失稳模式：(1)在筋高比1.0～4.5范围内，随着筋高比的提高，由于大筋刚度相对增大，失稳波形被更有效地抑制在大筋间的局部区域，此时，相对减小的小筋仍能对局域内蒙皮维持增强作用，使得多级加筋板的极限承载载荷值逐渐增大。从失稳波形的变化可看出，在筋高比1.0时结构发生整体失稳，只在中部产生一个横贯的大失稳波，而在筋高比2.5时横向失稳波数变为2个，失稳趋于局部化。(2)在筋高比4.5～5.0范围内，承载力曲线出现极值，此时小筋随着筋高比变大而刚度变小，在局部区域内对蒙皮的增强作用相应减弱，使得多级加筋板过早地发生局部屈曲进而导致失稳，因而承载力曲线开始呈现下降趋势。(3)在筋高比5.0～7.5范围内，小筋高度进一步降低，导致局部增强作用的弱化，x方向轴压更多地由抗压刚度增大的大筋承担，使得大筋刚度对提高结构极限承载性能起主导作用，因而随着筋高比的提高，曲线呈现渐变增大的趋势。(4)在筋高比7.5～10.0范围内，大筋高度远大于小筋，其相应的抗压刚度也远大于小筋，因此大筋作为主要的承力结构，而小筋的作用主要表现为抑制局部失稳的抗弯能力。

图4给出了各筋高比对应的极限承载时的应力云图，需要说明的是，白色区域为进入塑性的部分。由图4可知，作为主要承力结构的大筋与蒙皮开始大面积进入塑性，x方向轴压内力的重分布造成结构发生材料非线性失稳，这种失稳模式与材料屈服强度紧密相关，若不改变材料，则发生材料非线性失稳时的极限承载力将保持不变，这就造成了曲线趋于稳态。

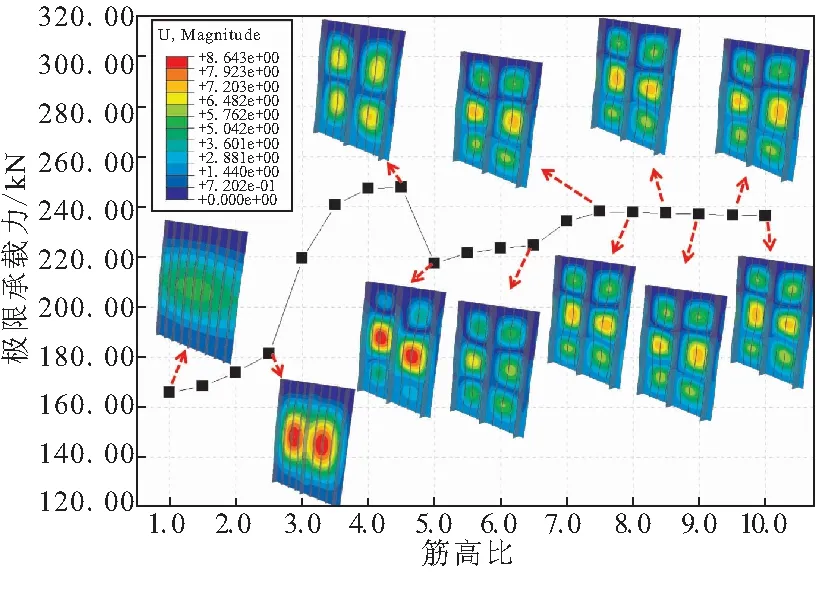
图3 完美多级加筋板结构筋高比-载荷曲线

图4 多级加筋板极限承载时刻的应力云图

对于本章算例而言，筋高比为1.0时的加筋板是单级加筋板，其极限承载力为极小值165.9 kN，而当筋高比为4.5时加筋板结构极限承载力为极大值247.8 kN，承载力提高了49.4%，此时发生了有利于保持承载力的失稳模式。这至少可揭示，若能合理地分配大小筋的刚度比，可有效提高多级加筋板的承载性能，且相较于传统单级加筋板具有更大的优化设计空间。

3 多级加筋板缺陷敏感度分析

从之前讨论的“失稳局部化”有利于保持结构承载力这一现象可预测到，多级加筋结构形式可能有利于抑制局部缺陷诱发的出平面变形，进而保持更高的极限承载力，表现出较好的抗缺陷设计潜力。

3.1 几何缺陷的表征

加筋板在制造、运输和使用过程中不可避免地会产生缺陷。本文通过改变模型节点坐标的方式将初始几何缺陷引入完美结构中，其表征方式如式(1)和式(2)所示：

X=XP+XI

(1)

XI=αδφ

(2)

式中XP表示完美结构的节点坐标矢量；XI表示几何缺陷引起的结构节点坐标偏移矢量；δ表示蒙皮厚度与筋条高度的和；φ表示归一化的缺陷基矢量，可以为单点凹陷、结构一阶特征值屈曲模态矢量等；α表示无量纲化的缺陷幅度，取值范围为[0,1]，当α=0时代表完美结构模型，α=1代表引入缺陷幅值最大时(幅值等于蒙皮厚度与筋条高度的和)的含缺陷模型。

3.2 单点凹陷缺陷

相较于其他初始缺陷形式，单点凹陷缺陷在工程实际中更为高发，在加筋板的加工、装配、运输和服役期间均有可能因为外力撞击而在结构表面产生。

在数值方法的实现上，本文采用与文献[19]相同的方法引入缺陷，即在蒙皮上施加法向集中力，以其为扰动载荷(Perturbation Load)，并将计算得出的节点坐标偏移矢量XI映射至完美结构，形成含缺陷的加筋板模型，如图5所示。

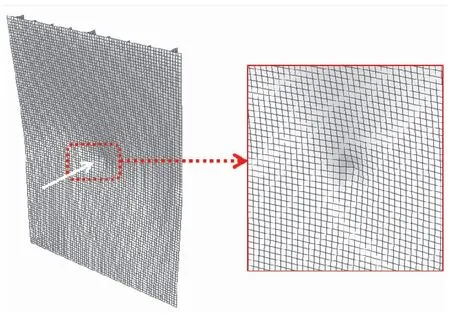
图5 单点凹陷缺陷示意图

3.3 多级加筋板缺陷敏感度分析

本文中单点凹陷缺陷敏感度分析的流程为：首先计算出完美加筋板模型轴压下的极限承载力；对完美加筋板模型施加扰动载荷，得到单点凹陷缺陷；将单点凹陷缺陷映射至完美结构形成含缺陷的加筋板模型，并计算其极限承载力；以含缺陷加筋板模型与完美结构模型的轴压承载力比值评价结构的抗缺陷能力，称其“折减因子”，该值越大，表示结构抗缺陷能力越强，缺陷敏感度越低。

针对第一章中的单级与多级加筋板模型开展单点凹陷缺陷敏感度分析。当施加的法向集中力为8 kN时加筋板产生的凹陷值为8.4 mm，接近于加筋高度和蒙皮厚度之和，以其作为大幅单点凹陷缺陷。同时，由于单点凹陷的产生具有不确定性，因而十分有必要考察不同幅度的凹陷发生在大筋、小筋和蒙皮等不同局部区域时对加筋板缺陷敏感度的影响，其布局示意图如图6。

图6 单点凹陷缺陷布局示意图

图7所示为单级与多级加筋板缺陷敏感度曲线，可看出不同的单点凹陷缺陷位置分布，会对加筋板的刚度有不同程度的折减，因而对极限承载力造成不同的影响。随着缺陷幅值的增大，单级与多级加筋板的极限承载力都呈下降趋势，但多级加筋板曲线下降幅度明显小于单级加筋板。发生大幅缺陷时(扰动载荷值为8 kN)，单级加筋板折减因子为0.64，而多级加筋板为0.77，可知多级加筋板具有更优异的抗缺陷能力、更低的缺陷敏感度。为了更清晰地揭示多级加筋板低缺陷敏感度的力学机理，本文以发生在Y4位置、扰动载荷为1 kN的小幅缺陷为例，给出含缺陷的单级与多级加筋板位移-载荷曲线，如图8所示。发现相较于单级加筋板，多级加筋板由于加筋形貌更为丰富，导致其局部抗弯刚度呈现周期性变化，可有效将缺陷诱发的局部失稳抑制在局部区域内，表现出更优异的抗缺陷能力。

图7 传统单级与多级加筋板单点凹陷缺陷敏感度曲线

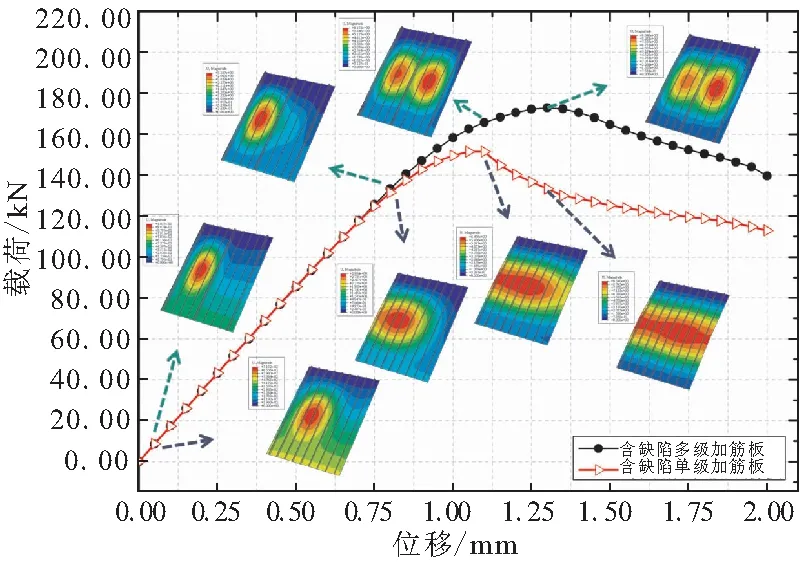
图8 含缺陷的传统单级与多级加筋板位移-载荷曲线

针对第一章中的多级加筋板模型，在结构Y4位置施加5 kN的法向集中力来引入单点凹陷缺陷，考察含缺陷模型的极限承载力随筋高比的变化趋势，并与第二章中由完美结构得出的变化曲线进行对比。结果如图9所示，同时给出了极限承载条件下加筋板的变形云图。随着筋高比的提高，含缺陷模型的极限承载力逐渐增大，这与第二章所得出的完美加筋板结构随筋高比的变化趋势有明显差异：完美结构情况下，筋高比的变化导致了不同的失稳模式，因而曲线并未呈单调变化趋势；而含缺陷多级加筋板具有较为一致的失稳模式，即由单点凹陷引发局部出现平面变形，使结构较早地进入局部屈曲，继而变形逐步增大导致结构失效。多级加筋板由于具有非均匀、层级化的刚度分布，可有效将变形抑制在相邻大筋之间，从而提高结构后屈曲承载能力，并且随筋高比增大，刚度层级化分布现象更为明显，造成结构对变形的抑制效果也逐渐增强，因而曲线表现出递增趋势。由图9可知，实现结构承载力最大化的设计目标时，完美与含缺陷结构的最优筋高比不同，因而在实际工程中需考虑缺陷对结构承载性能的影响。

图9 含缺陷多级加筋板筋高比-载荷曲线

4 结论

(1)相较于传统的单级加筋板结构，多级加筋板具有更优异的承载性能与抗缺陷能力，可作为航天领域一种新型结构储备。

(2)合理分配大小筋的筋高比可改变结构失稳模式，继而主动提升多级加筋板的承载效率，且相较于传统单级加筋板具有更大的优化设计空间。

(3)仅针对完美加筋板的结构设计在实际工程中易导致不合理的设计，应该采用基于缺陷敏感度分析的设计理念。

参考文献：

[1] Hao Peng,Wang Bo,Li Gang.Surrogate-based optimum design for stiffened shells with adaptive sampling[J].AIAA Journal,2012,50(11):2389-2407.

[2] Vasiliev V V,Barynin V A,Razin A F.Anisogrid composite lattice structures-development and aerospace applications[J].Composite Structures,2012,94(3):1117-1127.

[3] Bushnell D,Rankin C.Optimum design of stiffened panels with substiffeners[C]//46 th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,2005:1-54.

[4] Watson A,Featherston C A,Kennedy D.Optimization of postbuckled stiffened panels with multiple stiffener sizes[C]//Proceedings of the Forty Eighth AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,Honolulu,Hawaii,2007:23-26.

[5] Murphy A,Quinn D,Mawhinney P,et al.Tailoring static strength performance of metallic stiffened panels by selective local sub-stiffening[C]//Proceedings of the Forty Seventh AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference. Newport,Rhode Island,2006:1-4.

[6] Quinn D,Murphy A,McEwan W,et al.Non-prismatic sub-stiffening for stiffened panel plates-stability behaviour and performance gains[J].Thin-Walled Structures,2010,48(6):401-413.

[7] Quinn D,Murphy A,McEwan W,et al.Stiffened panel stability behaviour and performance gains with plate prismatic sub-stiffening[J].Thin-Walled Structures,2009,47(12):1457-1468.

[8] 梁东平,徐元铭,彭兴林.复合材料格栅加筋板布局优化设计[J].固体火箭技术,2008,31(5):527-530.

[9] 荣晓敏,徐元铭,吴德财.进化神经网络在复合材料格栅结构设计中的应用[J].固体火箭技术,2006,29(4):305-305.

[10] Paulo R M F,Teixeira-Dias F,Valente R A F. Numerical simulation of aluminium stiffened panels subjected to axial compression: Sensitivity analyses to initial geometrical imperfections and material properties [J].Thin-Walled Structures,2013,62:65-74.

[11] 郝鹏,王博,李刚,等. 基于缺陷敏感性分析的加筋圆柱壳结构设计[J].应用力学学报,2013,30(3):344-349.

[12] Wang Bo,Hao Peng,Du Kai-fan,et al.Knockdown factor based on imperfection sensitivity analysis for stiffened shells[J].International Journal of Aerospace and Lightweight Structures,2011,1(2):315-333.

[13] Hao P,Wang B,Li G,et al .Surrogate-based optimization of stiffened shells including load-carrying capacity and imperfection sensitivity[J].Thin-Walled Structures,2013,72:164-174.

[14] Rigo P,Sarghiuta R,Estefen S,et al.Sensitivity analysis on ultimate strength of aluminium stiffened panels[J].Marine Structures,2003(16):437-468.

[15] Lynch C,Murphy A,Price M,Gibson A.The computational post buckling analyses of fuselage stiffened panels loaded in compression[J].Thin Walled Structures,2004,42:1445-1464.

[16] Yoon J W,Bray G H,Valente R A F,et al. Buckling analysis for an integrally stiffened panel structure with a friction stir weld[J].Thin-walled Structures,2009,47(12):1608-1622.

[17] 郝鹏,王博,李刚,等.基于代理模型和等效刚度模型的加筋柱壳混合优化设计[J].计算力学学报,2012,29(4): 481-486.

[18] Lanzi L,Giavotto V.Post-buckling optimization of composite stiffened panels:computations and experiments[J].Composite Structures,2006,73(2):208-220.

[19] Calladine C R.Understanding imperfection-sensitivity in the buckling of thin-walled shells[J].Thin-Walled Structures,1995,23(1):215-235.