多相稀薄流动中的颗粒相变研究①
2014-03-15胡建峰刘绪博
刘 英,李 洁,胡建峰,刘绪博
(国防科技大学 航天科学与工程学院,长沙 410073)
0 引言
高空固体火箭工作时,通常会产生含有铝氧化物的尾喷流场,大小不同、形态各异的铝氧化物在流场中质量分数可达30%,铝氧化物的存在会对尾喷流场产生显著的影响,特别是其中的主要成分Al2O3颗粒发生的相变过程,不仅会造成颗粒本身相态的变化,也会因为相变热的释放而影响气相流场的特性参数。因此,国内外针对稀薄环境下多相流场开展了众多研究,密歇根大学的Boyd[1-4]课题组利用Gallis[5]推导的单个球形颗粒热力学模型,基于分子动力学理论,实现了颗粒相对气相作用的DSMC(直接蒙特卡洛模拟)模拟,建立了双向耦合的气粒两相相互作用模型。同时,探讨了颗粒的非球形效应、颗粒旋转、颗粒相变和颗粒红外、紫外辐射特性。Gimelshein[6-8]课题组在美国空军经费支持下,采用基于DSMC(直接蒙特卡洛模拟)方法的SMILE软件,研究了高空固体姿控发动机的横向羽流流场,采用N-S/DSMC(纳维斯托克斯方程数值求解/直接蒙特卡洛模拟)不同算法,沿羽流轴线方向分区计算,数值模拟了羽流连续/稀薄混合流动。何小英等[9]通过采用坐标转换方法计算了气体分子在颗粒表面的反射,进而研究了带液相颗粒的两相羽流场。张斌等[10]采用DSMC/EPSM(直接蒙特卡洛模拟/平衡粒子算法)混合算法,结合稀薄流中气粒耦合作用模型,开展了固体微推力器羽流场中气粒两相稀薄流动的数值研究,研究了羽流场中气粒两相参数的分布规律和气相组分分离效应。
本文采用DSMC(直接蒙特卡洛模拟)方法,研究了真空环境下的多相稀薄流动相关问题,着重探讨了颗粒相变模型作用时对气相的影响,以及不同粒径和不同热适应系数条件下颗粒温度的变化规律。通过和国外文献的对比,表明本文采用的数值方法是正确的,计算结果具有较高的可靠性。
1 相变模型研究
颗粒相相变在含有金属添加剂的固体火箭发动机高空工作时产生的羽流场中占据着重要的位置,它不仅能够影响到颗粒本身的温度和相态,也会对周围的气相分子形成影响,特别是会对羽流场的辐射特性造成重大影响。本文模型使用的粒子相变潜热采用的是适应液态直接到稳态α相的相变潜热,因此只考虑主要的结晶过程亚稳相γ相的形成,忽略近场区中广泛存在于小粒径颗粒中的由γ相向稳态α相过渡的过程。在氧化铝颗粒结晶动力学标准模型中,一致假设当液态的球形颗粒在温度冷却到显著低于熔点温度Tm的结晶温度Tf时,才开始发生相变,一旦相变开始,颗粒结晶就由颗粒表面向核心不断发展,结晶的锋面速度可用下式给定[11]:
(1)
式中Tj和rj分别代表粒子温度和半径;r1代表结晶锋面所处半径同rj的比值;参数A和n为常数,A=2.7×10-6ms-1K-1.8,n=1.8,取自Plastinin文献[12]。
r1变化反过来会影响粒子的温度,通过以下的能量平衡方程来建立二者的关系:
(2)

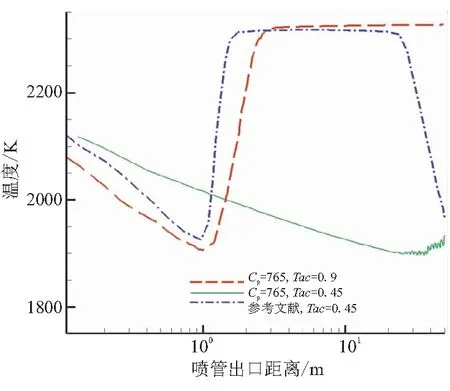
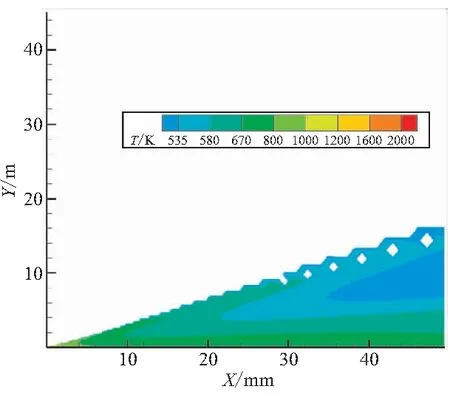
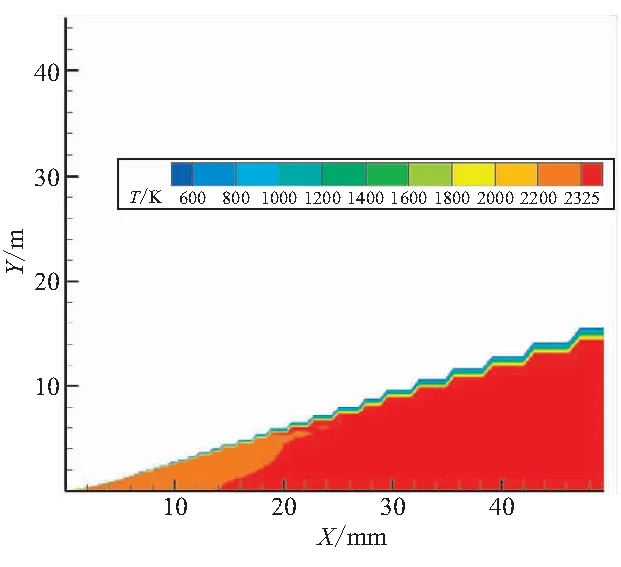
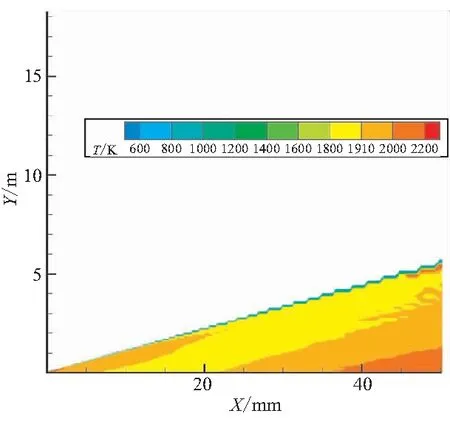
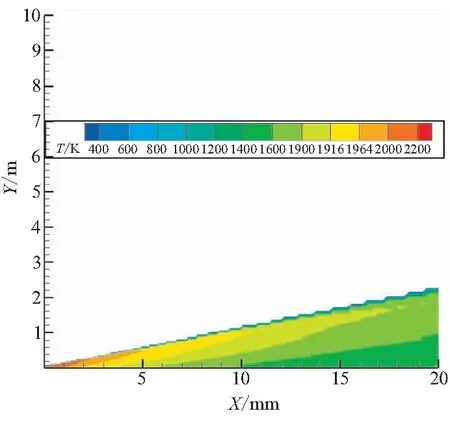
颗粒温度的瞬变和相间热传导率之间的关系在模型中分为3个阶段:固化、熔解、纯相期间的加热和冷却。首先,如果条件满足Tf (3) 式(3)可适用于所有网格中的粒子,即使在颗粒相与气相粒子相互作用可忽略的区域和网格也可应用。对于正处于固化过程中的粒子,在相间作用可忽略的区域,有可能会碰到很大的相对当地时间Δt这样一种情况。这种情况的存在,进而在计算ΔTj的过程会产生大的离散误差,最终结果就是会让颗粒温度Tj超出其熔化温度Tm。为了避免这种情况的出现,在模型的数值建构中设置了一个变量N,使其等于满足不等式N>50×ΔTj/Tm的最小整数。如果N>1,Tj和r1的初始值重新赋给该粒子,时间步长被分为N个整数段,每段长为Δt/N,以上步骤迭代N次,直到计算出最后的Tj和r1。 (4) 最后一种情况就是粒子既不处于固化过程,也不处于熔解过程,其温度调整由下式控制: (5) 依据上述相变模型,耦合气粒两相相互作用模型,同时考虑粒子的碰撞、聚合、分离,对二维两相稀薄羽流场进行了模拟。 计算域为从喷管出口平面向下延伸100 m,向外扩展40 m的矩形区域。喷管出口处的直径为7.85 cm。气体为N2、H2和CO的混合物,气相之间的碰撞为可变硬球碰撞模型。在出口平面,气体的速度达到了3 113 m/s,温度为1 433 K,密度为0.011 kg/m3,其摩尔分数H2为0.38,N2和CO各占0.31,周围环境为真空。 颗粒相具有一个离散的尺寸分布,分为7个不同的种类,直径范围从0.3~6 μm之间。由于喷管出口有用的流场信息的缺乏,采用了Anfimov[14]给出的在喷口截面颗粒性质分布数据,并认为在整个出口平面内是相同的(见表1)。 设颗粒表面的热适应系数为0.9,这样90%涉及到漫反射的相间碰撞都完全适应了颗粒温度,其余的10%涉及到了镜面反射。相间的动量和能量转换用双向耦合法进行计算,用一个非平衡的相变模型描述液态Al2O3小滴的结晶化作用。相变模型解决了温度对于结晶率和相关放热的依赖,并忽略了固态Al2O3的γ-α的转变以及不同相密度的差异。 在气相分子和颗粒相互作用时,气相对颗粒相的作用采用Gallis[15]推导的单个球形颗粒热力学模型,至于颗粒相对气相力与热的作用及算例的验证在文献[16]中进行了完备叙述。 表1 喷流出口颗粒相参数分布 为增加对比性,主要考察沿X=0 m,Y=0.02 m;X=50 m,Y=5 m这一抽取线上流场参数变化。图1中,所引用参考文献数据均来源文献[17],从温度的变化趋势看,再从图1对比分析可知,相变与否对气相分子的温度变化影响有限,模型计算所得的气相温度变化同文献吻合较好,与文献数据比起来,在喷口至下游8 m范围内文献结果要大于本文模型计算结果,在8 m至下游50 m则相反。这一差异的存在主要归因于文献中颗粒在出口截面是以非均匀速度出射的,沿Y向有一个速度梯度的变化。 图1 沿抽取线相变与否气相温度变化 由于喷管具体参数无法获取,本文将出口截面粒子速度均匀化处理,这会使颗粒散布范围减小,对气相分子的影响范围也随之减小,使得在同一抽取线下,气相分子温度要低于文献值。通过计算发现,颗粒相的存在以及颗粒相变模型的作用会使得气相分子温度升高,压强变大,马赫数减小,这也符合气粒两相作用的基本规律。 从图2中 0.4、4 μm 颗粒温度变化与文献结果的比较可发现,由于本文计算并未耦合辐射模块,对于小粒径颗粒在下游区辐射热强于相变热,故温度会低于本文计算结果,大粒径颗粒则不同。 (a)0.4 μm颗粒温度变化 (b)4 μm颗粒温度变化 在图2(b)中,相变区文献计算结果要高于本文结果。所以,在喷口附近数米范围内文献数据大于本文计算数据。因这两种作用综合影响,在相间相互作用时,在喷口附近数米范围内文献数据大于本文数据,而在下游则刚好相反。在相变与未发生相变的模型中,颗粒相的表现差异较为明显,就0.4 μm 来看,在图2(a)中未相变的情况下,颗粒的温度变化主要受相间作用模型的支配,颗粒温度高于周围气相温度,故热量不断由颗粒传递至周围气相分子,颗粒温度在一个变化不大的温度梯度下不断降低,在相变作用下,颗粒温度在整个变化过程中都要比未相变的情况下要高,这是由于颗粒在相变过程中不断放热造成的。从其变化的梯度也可看出,随着离开喷口距离越来越远,温度下降梯度不断减小,这是因为随着下游距离的增加,相变颗粒不断增加释放的热量越多所致。图2(b)中未相变时,4 μm 粒径颗粒的温度变化趋势与0.4 μm 粒径颗粒相似,全程温度梯度没有明显变化;相变时,4 μm 粒径颗粒的温度变化与0.4 μm 粒径颗粒的温度变化比起来,最大的不同就是在喷口附近经历了一个“V”字型的温度阶跃过程,这是由于4 μm 颗粒在喷口截面液相质量分数为1,温度为2 178 K,高于Al2O3颗粒的各向同性结晶温度,从喷口出来后,在气粒间对流传热作用下,温度逐渐降低,当温度低至Al2O3颗粒的各向同性结晶温度时,颗粒相变开始,一个对称的结晶锋面开始从粒子表面快速向核心运动,在此相变的过程中会放出热量,这部分热量被粒子吸收反过来又会使结晶锋面的推进速度变慢,减缓粒子的相变进程,到一定时候,当粒子相变所释放的热量与颗粒同气相分子的对流传热和粒子本身的辐射放热相当时,粒子就会处于一种温度静止的准平衡过程,而随着下游距离的不断增大,颗粒液相质量分数不断减小,通过相变来释放的热量越来越少,当相变热不足以平衡对流传热和辐射传热时,颗粒的温度就会脱离准平衡状态,不断下降,在图3中准平衡态后,没有出现温度下降的情况是在该计算中尚未将辐射模型耦合进来。 图3~图8为Cp=765 J/(kg·K)条件下,热适应系数(Tac)分别为0.9和0.45时,各粒径颗粒沿抽取线的温度变化图。观察对比一系列的温度变化图可发现,热适应系数为0.45时,颗粒温度普遍要比0.9时要高。 在图3中,气相温度随抽取线的变化,在喷口附近因气相分子的急速膨胀热能迅速转化为动能,导致该区域下降梯度最大,温度变化最为剧烈,随着下游距离的增加,分子间碰撞频率降低,温度下降梯度减小,在流场远场区,气相温度已经接近0 K。在热适应系数为0.45时,气相温度要比0.9时要低,并随着远离喷口距离的增加,这种趋势更加明显。这主要是因为随着距离的增加,气相分子的数密度不断减小,单位热量的传递产生的影响变得更加突出。本文计算结果同文献的差异分析同上。图4、图5为不同热适应系数及不同粒径沿抽取线颗粒温度对比图。 图3 不同热适应系数下沿抽取线气相温度对比 (a)0.4 μm颗粒温度对比 (b)4 μm颗粒温度对比 在图5中, 0.6 μm 颗粒温度基本呈下降趋势,只在出口很小范围内有非常短暂的温度静止“准平衡状态”;1 μm 颗粒温度变化线图中已经可观察到明显完整的“V”字型的温度阶跃过程,这说明在当前计算条件下,颗粒粒径大于1 μm的颗粒都能够支撑一个明显的“V”字型的温度阶跃过程;但2 μm 粒径颗粒中没有观察到明显的温度阶跃过程,造成这一现象的主要原因就是2 μm 粒径颗粒在出口截面上较其它大粒径颗粒温度要低,只有1 920 K,稍高于相变结晶温度,不足以支撑一个明显的温度阶跃过程。 图5 不同热适应系数及不同粒径沿抽取线颗粒温度对比 由图4、图5均可看出,温度静止的“准平衡状态”维持时间也会相对变长,1、4 μm 颗粒清晰可见。通过本文结果和文献结果的对比可知(见图4),在热适应系数为0.45时,0.4 μm 颗粒文献数据要小于本文计算结果,4 μm 颗粒本文计算结果没有完整温度阶跃出现,这主要是因为辐射模型的缺失。此外,本文在喷口截面粒子速度数据的给定只有轴向速度,对于径向速度进行了忽略处理,这造成了颗粒相径向散布范围小于文献。因此,抽取线角度的选取要略小于文献,更靠近轴线颗粒高温区,这也可能是造成计算结果同文献的差异。 由不同热适应系数下0.4、4 μm颗粒温度变化云图(图6~图8)可见,因热适应系数减半,亦即以漫反射为作用机制的相间碰撞频率削减一半。因此,颗粒相和气相间的热传递率大概也会减小成为原来的50%,颗粒对周围气相分子的加热效应将显著降低。颗粒发生相变的时间将有一定的延迟,这一点在小粒径颗粒上表现并不明显,这主要是因为小粒径颗粒本身出口截面温度较低,液相质量分数占据比例较小,而温度变化率又与颗粒粒径成反比所致。通过对比可发现,计算结果在趋势变化上和文献吻合较好,在下游区大粒径颗粒出现的温度下降现象主要归因于颗粒的辐射传热作用,而本文未将辐射模型嵌入进来。因此,在4 μm颗粒温度变化中没发现下降现象。 (a)热适应系数Tac=0.9 (b)热适应系数Tac=0.45 (a)热适应系数Tac=0.9 (b)热适应系数Tac=0.45 图8 热适应系数0.45时沿抽取线喷口附近4 μm颗粒温度云图 (1)相变模型对不同粒径颗粒影响效果不同,对大粒径颗粒的影响大于对小粒径颗粒的影响。分析原因:一方面,小粒径颗粒在出口截面液相质量分数较小温度较低;另一方面,粒径小导致颗粒与气相分子接触面积增大,对流换热剧烈。所以,颗粒自喷口出来后,温度沿抽取线变化差别较大,小粒径颗粒温度不断下降,下降梯度随下游距离的增加逐渐减小。大粒径颗粒温度变化则基本可分为3个阶段:“V”字型温度阶跃过程、温度静止“准平衡”过程、温度不断下降过程。 (2)在大粒径颗粒中,随颗粒粒径的变大,3个过程在流场中所占范围也逐次变化。其中,温度静止“准平衡”过程变化最具代表性,粒径越大,该过程持续时间越长,所占流场范围最大。 (3)通过和文献计算结果进行对比,表明了本文采用的碰撞-聚变-分裂模型的正确性以及基于此颗粒相变模型采用的数值方法的正确性。 参考文献: [1] Burt J M,Boyd I D.Evaluation of a Monte Carlo model for two phase rarefied flows[R].AIAA 2003-3496. [2] Burt J M,Boyd I D.Particle rotation effects in rarefied two phase plume flows[C]//24th International Symposium on Rarefied Gas Dynamics,Monopoli,Italy,2004. [3] Burt J M,Boyd I D.Development of a two-way coupled model for two phase rarefied plume flows[R].AIAA 2004-1351. [4] Burt J M,Boyd I D.A Monte Carlo radiation model for simulating rarefied multiphase plume flows[R].AIAA 2005-4691. [5] Gallis M A,Torczynski J R,Rader D J.An approach for simulating the transport of spherical particles in a rarefied gas flow via the direct simulation Monte Carlo method[J].Physics of Fluids,2001,13(11):3482- 3492. [6] Sergey F Gimelshein,Alina A Alexeenko.The influence of particulates on thruster plume/shock layer interaction at high altiyudes[R].AIAA 2005-766. [7] Sergey Gimelshein,Gennady Markelov,Jean Muylaert.Numerical modeling of low thrust solid propellant nozzles at high altitudes[R].AIAA 2006-3273. [8] Natalia E Gimelshein,Sergey F Gimelshein,Robert B Lyons,et al.Numerical prediction of UV radiation from two-phase plumes at high altitudes[R].AIAA 2007-1014. [9] 何小英,贺碧蛟,蔡国飙.直接模拟蒙特卡罗羽流模拟的两相作用模型[J].推进技术,2011,32(2):214-219. [10] 张斌,毛根旺,胡松启,等.固体微推力器气粒两相羽流场的数值模拟[J].固体火箭技术,2011,34(3):314-318. [11] Jonathan M Burt,Iain D Boyd.Monte Carlo simulation of a rarefied multiphase plume flow[R].AIAA 2005-964. [12] Yu A Plastinin,Sipatchev H P,Karabadzhak G F,et al.Experiment investigation of alumina particle's phase transition and radiation[C]//AIAA Paper 98-0862,36th AIAA Aerospace Sciences Meeting,Reno,NV,1998. [13] Hunter S C ,Cheery S S,Kliegel J R,et al.Gas-particle nozzle flows with reaction and particle size change[C]//AIAA Paper 81-0037 ,19th AIAA Aerospace Sciences Meeting,St.Louis,Mo,1981. [14] Anfimov N A,Karabadjak G F,Khmelinin B A,et al.Analysis of mechanisms and nature of radiation from aluminum oxide in different phase states in solid rocket exhaust plumes[C]//AIAA Paper 93-2818,28th AIAA Thermophysics Conference,Orlando,FL,1993. [15] Gallis M A,Torczynski J R and Rader D J.An approach for simulating the transportof spherical particles in a rarefied gas flowvia the direct simulation Monte Carlo method[J].Physics of Fluids,2001,13(11):3482-3492. [16] 李洁,尹乐,颜力.稀薄流气粒两相耦合作用的热力学模型[J].国防科技大学学报,2009,31(3):6-10. [17] Jonathan M Burt,Iain D Boyd.High altitude plume simulations for a solid propellant rocket[R].AIAA 2007-1013.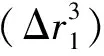
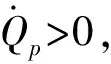
2 计算条件描述

3 计算结果与分析








4 结论
