旋转弹锥形运动发生区间及频率特性研究①
2014-03-15任天荣马建敏
任天荣, 马建敏
(1.复旦大学 力学与工程科学系,上海 200433;2.上海机电工程研究所,上海 201109)
0 引言
旋转弹(包括旋转导弹、旋转火箭弹)的主动段飞行中,在没有操纵指令的情况下,时常也会产生明显的锥形运动,此运动又具体有摆幅收敛、摆幅稳定和摆幅发散(即发生"掉弹")3种现象。后2种运动状态会导致飞行姿态的改变,进而影响增加脱靶量、降低射程。对于锥形运动的发生原因国内外已有一些研究,Thomson指出了旋转弹体的自旋轴为其最小主惯性轴时,因弹体系统总是存在不可避免的能量耗散,这就使得弹体存在锥形运动的发散趋势[1];后来Likins在其NASA 报告[2]中也给出结论:A spacecraft spinning about its minor axis in the presence of energy dissipation is directionally unstable。弹体的锥形运动可看作是弹轴相对速度矢量的章动和进动运动的合成,Platus认为弹体的滚转运动实际上包含弹体绕自身纵轴的滚转和弹轴绕速度矢量的进动,进动角速率与弹体的极转动惯量和赤道转动惯量之比有关,并且当内部质量存在轻微不对称时,弹体绕纵轴的滚转轴将与弹体最小转动惯量轴不重合,这一现象会导致章动角的产生,也是诱发弹体姿态发散的一个因素[3]。Morote和Liano分析了140 mm火箭的卷弧翼的气动特性,尤其是展长和弦长对飞行动稳定的影响,发现减小卷弧翼弦长可使面外力和面外力矩加大,使火箭弹动稳定性变差,易导致锥形运动发生,而减小展长不利于弹体的静稳定性,却有助于改善飞行器的动稳定性[4]。Murphy针对无控弹体,采取一阶线性化方法,得出了系统动态稳定性区域,给出了旋转弹体动态稳定性必须满足的条件,说明了面外力矩在引起一个圆运动收敛的同时造成另外一圆运动的发散[5-6]。张涵信等研究了飞船返回舱俯仰振荡的动态稳定形态随来流马赫数的变化,指出当来流马赫数等于某一临界马赫数时,开始发生动态Hopf分叉,产生周期振荡的极限环[7]。洪金森和洪诗权应用多尺度法获得了再入飞行器运动方程的极限环振幅和频率的渐近表达式,并指出系统的稳定性取决于阻尼线性项的符号变化[8]。毛雪瑞基于弹体的短周期运动建立了弹体的章动角运动模型,并得出了锥形运动的渐进稳定性判据和有界稳定性判据,指出了增大静稳定力矩系数、减小侧向力矩系数有利于改善锥形运动稳定性,并指出了弹体处于临界稳定状态时弹体将存在稳定的进动角速率[9]。上述相关结果均是基于飞行器质量不变的前提。在文献[10]中给出了基于变质量运动方程,关于锥形运动(极限环)存在的理论证明,但没有对其产生的条件加以说明。实际上,正常稳定的飞行相当于弹体轴线关于来流夹角的定常解,锥形运动则为弹体轴线关于来流夹角的周期解,这一现象正对应于数学中的常微分方程的极限环。
本文将从变质量陀螺方程出发,分析关于旋转导弹姿态运动极限环的发生的区间范围,对旋转导弹产生锥形运动的条件进行探讨,并基于微分方程定性理论中关于极限环的理论成果[11-12],研究分析关于旋转导弹姿态运动的极限环存在发生的区间范围,对旋转导弹产生锥形运动的条件进行探讨,并基于矩阵代数的理论成果,给出一个分析锥摆频率的公式。
1 基于变质量陀螺运动方程的旋转弹姿态方程
因为主动段飞行过程即导弹变质量过程,故下面先给出变质量陀螺的普遍方程,推导见文献[13-14]:
(1)
其中:
Mi=(Mix,Miy,Miz)

这里将附加质量的结合过程看作是绝对的非弹性碰撞。随后,采用文献[10]中使用的端面燃烧旋转导弹变质量陀螺运动方程。即设一圆柱体旋转导弹做静稳定水平飞行,则其速度坐标系近似为惯性坐标系,设原点即为弹体质心;而取弹体的半弹体坐标系为相对转动的动坐标系。将惯性坐标系中动量矩定理的微分过程改在动坐标系内进行,则有
(2)
其中,带“~”的微分符号表示动坐标系的局部导数;ω为相对动坐标系的瞬时角速度。则有
(3)
(4)
考虑到在半弹体坐标系中,全弹体转动惯量是由弹体和将要离去的燃气质量组成的,则式(4)为
ω×(J·ω)=M
(5)

式中R为燃烧室半径;l为弹体长度。
为方便计算,下面令Jx=J1。再与方程(1)综合之,得端面燃烧旋转导弹变质量陀螺运动姿态方程:
(6a)
(6b)
(6c)
2 弹体运动动态判据分析
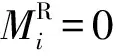
(7a)
(7b)
化方程(7a)、(7b)为
(8a)
(8b)

(9a)
(9b)
(9c)
(9d)
显然,方程组(9)是一线性系统,原点为其平衡点。由一次近似稳定理论知,当系统(9)的Jacobi矩阵所有特征值的实部均为负时,该系统是零解渐近稳定的[15]。其Jacobi矩阵为
(10)
其Jacobi矩阵行列式为
λ4+2Bλ3+(A2+B2-(my+Δ′+mz))λ2-
B(my+Δ′+mz)λ+(my+Δ′)mz=0
(11)
下面再引用2个定理[12,16]:
定理1实系数代数方程
λn+a1(μ)λn-1+…+an-1(μ)λ+an(μ)=0
(12)
所有根均具有负实部的充分必要条件是所有的Hurwitz行列式均大于零,即
Δi>0(i=1,2,…,n)
定理2若实系数代数方程(12)具有一对纯虚根±ωi,其余n-2个根均具有负实部,则
(13)
于是对于系统(9)可得
Δ1=a1=2B>0
a2=A2+B2-(my+Δ′+mz)>0
a3=-B(my+Δ′+mz)>0
a4=(my+Δ′)mz>0
=B(2(A2+B2)-(my+Δ′+mz))
=B2((my+Δ′-mz)2-2(A2+B2)(my+Δ′+mz))
=a4Δ3=B2((my+Δ′-mz)2-2(A2+B2)(my+Δ′+mz))(my+Δ′)mz
由前面静稳定假设可知,my<0,mz<0,而干扰力矩系数Δ′>0,当my+Δ′<0时,可确保Δ1>0,Δ2>0,Δ3>0,Δ4>0,此时系统是渐近稳定的。由此知,静稳定设计的旋转导弹,微小扰动Δ′<-my,所造成的弹体姿态摆动会迅速收敛,但当扰动较大,使得系统(9)关于零点不稳定。其实,由上面看出,对系统(9)总有Δ1>0;又因对于通常的旋转导弹,有A2+B2≫|my+mz|,故而系统也总有Δ2>0;又由Δ4=a4Δ3,知当mt+Δ′<0时,均有Δ3>0,Δ4>0;而当my+Δ′+mz>0时,因一般对旋转弹箭A2+B2≫my+Δ′+mz,故此时Δ3<0,a4<0,从而Δ4>0,根据定理1所述,知此时系统必有一特征根实部大于零,即系统发散。因此,当Δ′<-my时,系统(9)肯定关于零点渐近稳定;当Δ′>-my-mz时,系统(9)肯定发散,即弹体姿态会不可回复到原有的飞行方向,若将操纵力也视为干扰力,则此时也可视弹体处于操纵机动状态;由此分析知,仅当-my≤Δ′≤-my-mz时,系统(9)才有可能发生锥形振荡运动,即干扰力矩导致系统分叉发生的临界点必在区间[-my,-my,-mz]上。实际飞行中,弹体可能遇到的干扰有“3秒跳”、舵翼分离流动的干扰、发动机熄火、发动机内流场激扰、推力偏心及气动力偏差等。

3 旋转弹体振荡频率的分析

(14)

图1 旋转弹体锥形运动发生区域示意图
(1)当系统没有受到干扰,且不计其陀螺稳定项与尾喷流章动阻尼项,即Δ′=0,A=0,B=0,则其振荡频率为

(2)当系统没有受到干扰,但考虑其陀螺稳定项与尾喷流章动阻尼项,即Δ′=0,A≠0,B≠0,则弹体有阻尼振荡频率表示为
为方便计算,仍令mz=my,则有
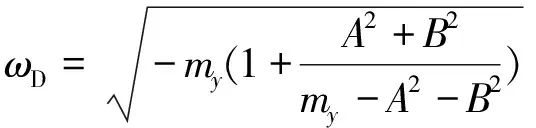
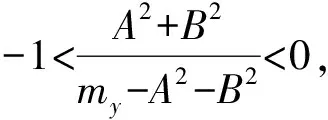
(3)当弹体系统处于小舵偏控制的机动状态(即将舵面偏打当成干扰力,且干扰力矩系数满足-my≤Δ′≤-my-mz),又考虑其陀螺稳定项与尾喷流章动阻尼项,即Δ′≠0,A≠0,B≠0,则此时弹体锥形运动的振荡频率,可称为小舵偏机动频率,其频率可表示为

4 关于锥形运动的进一步讨论
这里的分析是建立在线性系统之上的,由于实际飞行中系统应是非线性状态的,故而上面的分析是有局限性的,也就难以对弹体发生振荡运动的临界点,给出准确的结果,而仅能给出一个区间。旋转弹箭稳定的锥形运动,可视为一种在气动力非线性条件下的极限环运动,在文献[9]中,基于微分方程定性理论中的Bendixson-Dulac定理[18],从理论上说明了弹体稳定锥形运动存在性,但那是在阻尼力矩线性条件下得出的结论,相对于真正飞行环境差异较大,也就没有多少对实际飞行现象的指导意义。下面讨论一下,当阻尼力矩非线性时的情形。
Bendixson-Dulac定理,给定微分方程组:
(15a)
(15b)
其中,Y、Z∈C1(D);D是环域,D中无奇点。若存在函数B(y,z) 、M(y,z)∈C1(D),B(y,z)>0且在环域D上有
(16)
而等号不能在整条轨线上成立,则在D上至多有一个极限环。若此极限环存在,则是稳定的。

=Y(y,z)-c1y3=Y1(y,z)
(17a)
=Z(y,z)-c4z3=Z1(y,z)
(17b)
再分别计算易得
(18)
(19)
(20)
(21)
则由
3z2(c1y2+c4z2)≤0
则当极限环存在判别式:
(22)
成立时,Bendixson-Dulac定理中的条件成立,可以确保此时的动力学系统,如果不收敛到零点,则系统必存在一个稳定的极限环。由以前的分析有
又由于c1、c4可以为负值,且故仅当弹体振荡角度非常小或阻尼力矩的非线性系数很小时,才能确保系统极限环存在判别式(22)的成立。

5 结论
(1)在外力条件稳定弹体自旋转速不变时,主动段飞行的旋转导弹,当干扰力矩系数小于气动静稳定力矩系数时,系统关于原点渐近稳定;当干扰力矩系数大于气动静稳定力矩系数的2倍时,系统发散;当干扰力矩系数介于气动静稳定力矩系数的1~2倍之间时,系统才会有锥形运动现象发生。
(2)旋转导弹采用气动静稳定设计,较小的振荡幅度和较低阻尼非线性,使得旋转弹体一旦进入锥形运动状态,就一定是稳定的锥形运动状态的充分条件。
(3)旋转火箭弹较大的气动静稳定度设计,是促使 “掉弹”现象发生的原因之一。
(4)主动段飞行的旋转导弹,其阻尼与干扰力矩对系统的运动周期是有影响的;弹体无阻尼振荡频率高于其主动段振荡频率;弹体主动段自由飞行振荡频率高于其小舵偏机动飞行的振荡频率。
参考文献:
[1] Thomson W T.Introduction to space dynamics[M].Wiley,New York,1961:212-214.
[2] Likins P W.Effects of energy dissipation on the free body motions of spacecraft[R].NASA TR 32-860,July 1966.
[3] Platus,D H.Missile and spacecraft coning instability[J].Journal of Guidance Control and Dynamics,1994,17(5):1011-1018.
[4] Morote J,Liano G.Stability analysis and flight trials of a clipped wrap around fin configuration[R].AIAA 2004-5055.
[5] Murphy C H.Free-flight motion of symmetric missiles[R].U.S.Army Ballistic Research Lab.,Rept.1216,July 1963.
[6] Murphy C H.Some special cases of spin yaw lock-in[J].Journal of Guidance Control and Dynamics,1989,12(6):771-776.
[7] 张涵信,袁先旭,叶友达,等.飞船返回舱俯仰震荡的动态稳定性研究[J].空气动力学学报,2002,20(3):247-258.
[8] 洪金森,洪诗权.再入飞行器极限环运动分析[J].空气动力学学报,2005,23(2):204-209.
[9] 毛雪瑞.卷弧翼火箭圆锥运动研究[D].北京: 北京理工大学,2006.
[10] 任天荣,马建敏.旋转固体火箭变质量运动特性分析 [J].固体火箭技术,2012,35(6):711-715.
[11] 马知恩,周义仓.常微分方程稳定性与稳定性方法[M].科学出版社(第1版),2001.
[12] 张继业,杨翊仁,曾京.Hopf分岔的代数判据及其在车辆动力学中的应用 [J].力学学报,2000,32(5) :596-605.
[13] K 马格努斯.陀螺理论与应用[M].贾书惠,等译.北京:国防工业出版社,1983:255-261.
[14] 任天荣.变质量陀螺方程在旋转导弹中的应用[J].弹箭与制导学报,2008,28(4):40-41.
[15] 刘延柱.陀螺力学[M].北京:科学出版社(第二版),2009:374-380.
[16] 陈文成,陈国良.Hopf分岔的代数判据 [J].应用数学学报,1993,29(5):251-259.
[17] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000.
[18] 张芷芳,丁同仁,黄文灶,等.微分方程定性理论[M].北京:科学出版社,1985:230-275.
[19] 任天荣,马建敏.基于陀螺力学的旋转导弹锥形运动分析[J].宇航学报,2010,31(9):2082-2087.
[20] 张涵信,冉政,呙超.关于飞船的动态稳定问题[J].空气动力学学报,1999,17(2):123-129.
[21] Flandro GA,Van Moorhem W K,et al.Fluid mechancis of spinning rockets[R],AFRPL ADA177350,1987:9-35.
[20] Yan Y,Mingori D L,et al.Stability of a spinning axisymmetric rocket with dissipative internal mass motion[J],Journal of Guidnnce,Control,and Dynamic,1997,20(2):306-312.
