一道高等代数考研题的注记*

范志勇，皇甫红琴

(1. 焦作师范高等专科学校 应用数学研究所，河南 焦作 454000；2.扬州大学 数学科学学院，江苏 扬州 225002； 3. 武汉城市职业学院 财经学院，湖北 武汉 430000)

引言：苏州大学2012年硕士研究生入学考试《高等代数》科目中的一道考研试题为：

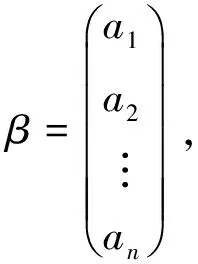
此题主要考察指定矩阵的行列式值和逆矩阵，如果按照通常的计算方法来求解的话，计算量大，难以做出结果，看似简单实则无从下手.那么，此题该如何求解呢？本文就从这样一道考研题入手，探索此题以及形如(λE-AB)或(E-AB)矩阵的行列式和逆矩阵的计算方法，尝试寻找此类型题的求解技巧和普遍方法.

1 主要结论

本文中，我们用|*|k表示k阶行列式，(*)m×n表示m×n矩阵，det(*)m×n表示m×n矩阵的行列式，Ek(或Ik)表示k阶单位矩阵，tra(*)表示方阵的迹，(*)T表示矩阵或向量的转置.

引理1 设A、B都是n阶方阵，则|λEn-AB|=|λEn-BA|.特别地，|En-AB|=|En-BA|.

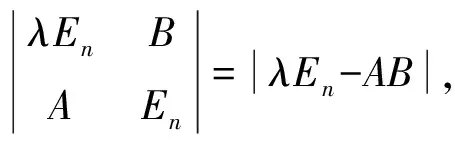
定理1 设A、B分别是m×n和n×m矩阵，λ≠0，则|λEm-AB|=λm-n|λEn-BA|.[1] [3]

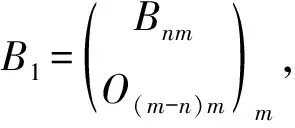
由引理1知，|λEm-A1B1|=|λEm-B1A1|，故|λEm-AB|=λm-n|λEn-BA|.证毕

推论1 |Em-AmnBnm|=|En-BnmAmn|

证明：在定理1中取λ=1立得.证毕.

推论2 设A是n阶方阵，A的秩为1，则

(1)|λEn-A|=|λEn-αβT|，其中α，β分别是n维非零列向量;[2]

(2)|λEn-ξηT|=λn-1|E1-ηTξ|，其中ξ，η分别是任意的n维非零列向量.特别地，当λ=1时，|En-ξηT|=λn-1|E1-ηTξ|.

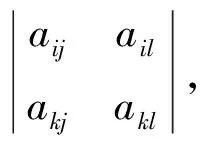
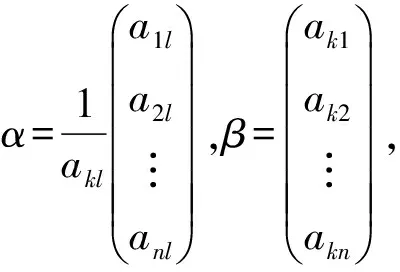
(2)设ξ，η分别是任意的n维非零列向量，则ξηT是n阶方阵，而ηTη是1×1矩阵，即ηTξ是一个数，再由定理1可得，|λEn-ξηT|=λn-1|E1-ηTξ|，易见当λ=1时，|En-ξηT|=|E1-ηTξ|.证毕.

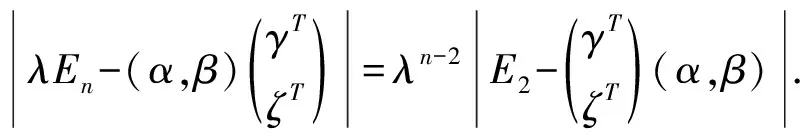
证明：由定理1和推论1立得.证毕.

定理1及推论1表明，可以将形如|λE-AB|或|E-AB|等高阶行列式的计算转化为低阶行列式计算，而推论2及推论3表明，对于秩为1或2的矩阵而言，此类高阶行列式计算甚至可以直接转化为1阶或2阶行列式计算，使得对高阶抽象型行列式的计算成为可能.那么，对于形如(E-AB)矩阵如何求逆？我们可以推导出如下定理.

定理2 设A、B分别是m×n和n×m矩阵，Em-AmnBnm可逆，则(En-BnmAmn)-1=En+B(Em-AB)-1A.

证明：因为Em-AmnBnm可逆，则|Em-AmnBnm|，由推论1知，|En-BnmAmn|≠0，从而En-BnmAmn可逆.又(Em-AB)(Em-AB)-1=Em，则(Em-AB)-1-AB(Em-AB)-1=Em.(1)

(1)式两边左乘B：B(Em-AB)-1-BAB(Em-AB)-1=B，则(En-BA)B(Em-AB)-1=B.(2)

(2)式两边右乘A：(En-AB)B(Em-AB)-1A=BA，则(En-BA)B(Em-AB)-1A+En-BA=En，

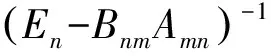
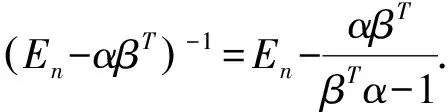
定理2及推论4确定了形如(E-BA)矩阵的逆矩阵的计算公式，特别是当BA的秩为1时，计算起来甚为简便.

2 应用

下面，我们选取历年来一些具有代表性的考研真题，对上述定理及推论加以应用.

例1(苏州大学)

解：(1)由推论2(2)知，|En-ββT|=|E1-βTβ|=|1-2|=|-1|=-1；

例2(中国科学院)设A、B分别是n×m和m×n矩阵，Ik是k阶单位矩阵.

(1)证明：det(In-AB)=det(In-BA)；

解：(1)由推论1立得.

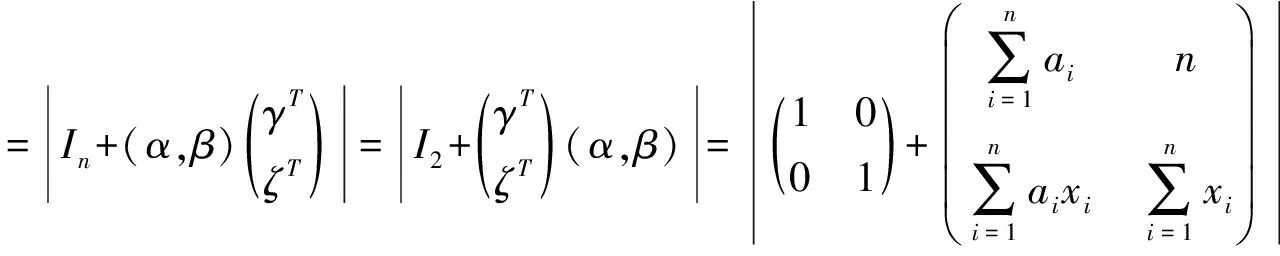
例3(清华大学)设n阶实方阵A如下，试求b的取值范围使A为正定方阵.

解：易见A是n阶实对称矩阵，考察A的各阶顺序主子式，不妨设Dk是A的k阶顺序主子式，则

再由推论2(2)得：

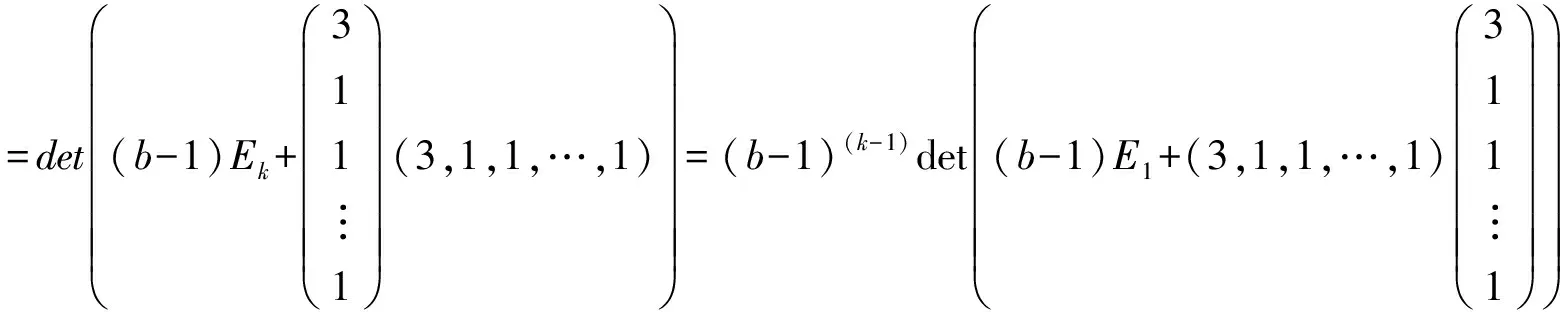
=(b-1)k-1|(b-1)E1+k+8|=(b-1)(k-1)(b+k+7)

注意到：A为正定方阵的充要条件是Dk>0(k=1,2,…,n).则b>1且b>-(k+7)，从而b的取值范围为b>1.(注：此题也可以直接计算Dk得出结论[4])

例4(吉林工业大学)设A、B分别是m×n和n×m矩阵，证明：AB的特征多项式fAB(λ)与BA的特征多项式fBA(λ)有如下关系：λnfAB(λ)=λmfBA(λ).

证明：AB的特征多项式fAB(λ)=|λEm-AB|，BA的特征多项式fBA(λ)=|λEn-BA|，则由定理1知，|λEm-AB|=λm-n|λEn-BA|，两边同乘λn得，λn|λEm-AB|=λm|λEn-BA|，即证.

例5(北京航空航天大学)设A、B分别是m×n和n×m矩阵，证明：AB与BA具有相同的非零特征值.

证明：设|λEm-AB|的标准分解式为：

λm-k(λ-λ1)(λ-λ2)…(λ-λk)，其中λ1,λ2,…,λk均不为0，则AB有k个非零特征值λ1,λ2,…,λk，由例4知|λEn-BA|=λn-k(λ-λ1)(λ-λ2)…(λ-λk)，即BA也只有这k个非零特征值λ1,λ2,…,λk，从而AB与BA具有相同的非零特征值，即证.

例6(中国科学院)设A、B分别是m×n和n×m矩阵，证明：traAB=traBA.

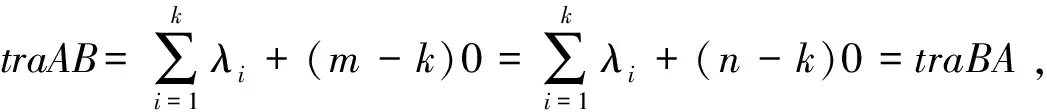
3 结论

本文主要研究了形如(λE-AB)或(E-AB)矩阵的行列式和逆矩阵的解法，探索了一些求解技巧，得到了一些求解公式.对于上述类型矩阵的行列式计算，我们将高阶行列式计算转化为低阶行列式计算，体现了行列式计算技巧中的降阶计算思想，可以称为“降阶法”，例1、例2、例3表明，这些求解公式解法简便、灵活，也易于掌握.例4、例5、例6则把这些求解公式应用于方阵的特征多项式、特征值和迹，进一步拓展了相关结论的应用范围，表明了它的适用性和可推广性.但是，本文只解决了形如(E-AB)矩阵的逆矩阵的求解方法，对于形如(λE-AB)矩阵的逆矩阵的求解，尚待进一步研究.

[参考文献]

[1] 北京大学数学系.高等代数(第三版)[M].北京：高等教育出版社，2003:203.

[2] 同济大学数学系.线性代数(第五版)[M].北京：高等教育出版社，2007:80.

[3] 刘洪星.考研高等代数辅导——精选名校真题[M].北京：机械工业出版社，2013:56.

[4] 王尊全.高等代数考研试题解析[M].北京：机械工业出版社，2009:91.

[2] 同济大学数学系.线性代数(第五版)[M].北京：高等教育出版社，2007:80.

[3] 刘洪星.考研高等代数辅导——精选名校真题[M].北京：机械工业出版社，2013:56.

[4] 王尊全.高等代数考研试题解析[M].北京：机械工业出版社，2009:91.