飞机最佳航路爬升时机研究
2014-03-14戴军,王健,王勇,李胜
戴 军,王 健,王 勇,李 胜
(1.民航华北空管局,北京 100621;2.天津空管分局,天津 300300)
飞机最佳航路爬升时机研究
戴 军1,王 健1,王 勇2,李 胜1
(1.民航华北空管局,北京 100621;2.天津空管分局,天津 300300)
确定飞机最佳航路爬升时机对提高飞行安全与效率有着重要意义。以北京区域管制的穿越间隔标准为例,根据几种典型航空器型号、起飞重量、不同高度层等相关因素,编程计算穿越高度层前所需的间隔,再考虑飞机调速情况做出修正,最终确定了航路飞行阶段飞机的最佳爬升时机。研究结果可提高管制员工作效率、增加空中交通流量,并可用于容量评估及空域规划研究。
航路爬升;飞行安全;间隔标准;空中交通流量
飞机最佳巡航高度层即为最省油高度层,飞机应尽可能地在最佳高度层飞行。对于部分繁忙航路,由于受到航路上方飞行的影响,管制员在较长时间内不敢指挥下方飞机及时上升高度,造成了飞机巨大的燃油消耗。对于飞机爬升前需满足的间隔,由于没有具体标准作参考,管制员仅依靠经验进行调配,极大地降低了工作效率。管制员工作负荷是限制空域容量的一个重要因素,预计在未来20年内空中交通需求将大幅增加[1]。为提高管制员工作效率、增加空中交通流量,确定航路飞行阶段飞机最佳爬升时机已成为一个亟待解决的问题。
国内外对该问题的研究主要通过建立碰撞风险模型[2-5],结合概率论计算碰撞概率,再与相关安全等级进行比较从而确定是否满足标准,其中最著名的就是Reich模型[2]。2010年,张勇等从概率论和交叉航路模型出发,建立了航路爬升时的碰撞概率模型,分别给出了同向穿越飞行和反向穿越飞行时初始距离与碰撞概率的关系[6]。
本文通过建立初步的数学模型,以北京区域管制的穿越间隔标准为例,根据几种常见航空器型号、起飞重量、不同高度层等相关因素,编程计算穿越高度层前所需的间隔,再考虑飞机调速情况做出修正,从而确定了航路飞行阶段飞机的最佳爬升时机。
1 飞机爬升性能计算方法
1.1 爬升率计算
由航路爬升时的动力学方程可得爬升率计算公式为


1.2 爬升时间和水平距离计算
工程上采用数值积分的方法,因而,飞机爬升至上一高度层所需的时间为

爬升至上一高度层所需的水平距离为

其中:Δh为相邻高度层的高度差;RCavg为爬升过程中的平均爬升率;Vavg为爬升过程中的平均水平速度[8]。
2 确定飞机最佳航路爬升时机的建模分析
2.1 爬升前所需间隔的计算模型
将飞机爬升穿越一次反向高度层,再爬升至上一个顺向高度层的过程视为一次爬升过程。则飞机爬升至最佳高度层的过程可细化为上述多次爬升过程的叠加。飞机A从现有高度层h1做第一次爬升会穿越一个反向高度层h2,此时A机与反向高度层上的B机做相对运动;A机在穿越高度层h2后会继续爬升至顺向高度层h3,此时A机与高度层h3上的C机、D机做同向运动。如图1所示。

图1 爬升穿越高度层Fig.1 Climb through levels
飞机爬升穿越反向高度层时,当飞机与h2层上的前机错过后,再考虑让飞机爬升,只需满足其与h2上后机B的间隔要求即可。飞机爬升穿越同向高度层时,必须与同向高度层上的2架飞机C、D都满足间隔要求,即


其中:DAB、DAC、DAD分别为飞机A爬升前与B机、C机、D机的水平距离;Sh1~h2、Sh1~h3分别为飞机从h1爬升至h2、h3所需的水平距离;th1~h2、th1~h3分别为飞机从h1爬升至h2、h3所需的时间;VB为B机在高度层h2上的平飞速度,VC、VD分别为C机、D机在高度层h3上的平飞速度。飞机需要同时满足式(5)~式(7),才能从高度层h1开始穿越高度层h2到达高度层h3。
2.2 参数选定
1)关于飞行速度,可按照各个机型推荐使用的飞行速度或指定的马赫数来确定;
2)关于风速,由于可认为相邻高度层上风速相差不大,并且若在同一数值风速下和取静风状态时计算是等效的,因此,可取静风状态下的数据进行计算;
3)关于温度,取ISA标准温度进行计算。
2.3 计算流程和实现方法
1)建立(机型起飞全重高度层风温度)数据库,对飞行速度等因素赋初值;
2)利用Matlab编程实现飞机最佳航路爬升时机模型,对输出结果进行分析研究,即求出在不同起飞重量下不同高度层上DAB、DAC、DAD的范围;
3)通过数据筛选和统计方法,对数据进行处理和分析。根据不同机型和飞机飞行重量,在不同高度层上进行数据分析绘图,经分析得出所需间隔的最大值;
4)最后,考虑飞机调速情况对计算结果做出修正,给出建议性的间隔要求。
3 算例分析
以北京区域管制为例,按照现行北京区域爬升穿越高度层的间隔标准进行计算,即反向穿越时,穿越后的间隔不小于50 km;同向穿越时,穿越后的间隔不小于20 km。飞机爬升的初始高度取5 400~10 400 m的全部可用高度层。考虑各主流中/重型机,以不同起飞重量进行研究。各机型详细参数如表1所示。

表1 机型详细参数Tab.1 Details and parameters of aircrafts
3.1 数据分析
采用波音主流飞机B737-700、B747-400F、B757-200、B777-200ER的0.9倍起飞全重(TOGW,take-off gross weight),计算在各高度层上所需要的反向穿越高度层前的DAB、同向穿越高度层前的DAC和DAD的最大值。由于计算情况繁多,考虑到结论的可行性,将合并情况进行总结,分别对不同机型在不同起飞全重下的结果进行绘图。
3.1.1 DAB分析
以0.9倍起飞全重为例,所需最大DAB如图2所示。
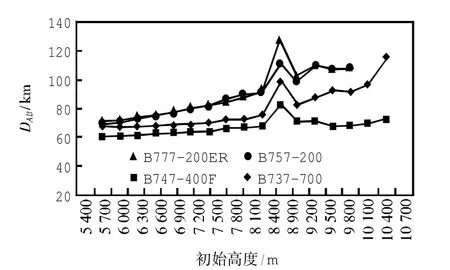
图2 0.9倍起飞全重下所需最大DABFig.2 Maximum required DABat 0.9 TOGW
通过图2可明显看出,随高度层升高DAB也有随之变大的趋势。在8 400 m为初始高度层时,由于与上一高度层的间隔为500 m,此时DAB较大。各机型爬升所需DAB如表2所示。

表2 各机型爬升所需(DAB)maxTab.2 Aircrafts’required(DAB)max
由表2可知:当起始高度非8 400 m时,116.2 km为DAB所需最大值;当起始高度为8 400 m时,所需最大DAB为127.3 km。
3.1.2 DAC分析
0.9倍起飞全重下所需最大DAC如图3所示。

图3 0.9倍起飞全重下所需最大DACFig.3 Maximum required DACat 0.9 TOGW
各机型爬升所需DAC如表3所示。

表3 各机型爬升所需(DAC)maxTab.3 Aircrafts’required(DAC)max
由表3可知:各机型所需最大DAC为27.4 km。
3.1.3 DAD分析
0.9倍起飞全重下所需最大DAD如图4所示。

图4 0.9倍起飞全重下所需最大DADFig.4 Maximum required DADat 0.9 TOGW
各机型爬升所需DAD如表4所示。

表4 各机型爬升所需(DAD)maxTab.4 Aircrafts’required(DAD)max
由表4可知:各机型所需最大DAD为26.1 km。
3.2 考虑飞机调速影响
该数据计算未涉及飞机调速情况,计算数据时是以在某个高度上某个机型推荐速度进行的。实际飞行中,一般会在推荐速度左右20 kn内进行调速,此时需考虑最不利的情况,计算飞机调速造成的误差。
3.2.1 计算误差

其中:1.9为平均爬升时间(min);270为B737-700的推荐速度(kn)。
3.2.2 修正结果
对3.1中得出的(DAB)max、(DAC)max、(DAD)max进行修正,得到

3.3 实例验证
利用雷达管制模拟机对计算结果进行模拟验证。选取不同机型在不同高度层上进行穿越爬升,飞机爬升时机为计算结果,将穿越后的间隔与北京区域现行间隔标准进行对比从而判断结果是否可行。大量真实模拟表明,计算结果准确可靠。单次模拟飞机穿越爬升如图5、图6所示,爬升起始高度为5 700 m,4架飞机均为空客A330。

图5 6 000 m时飞机相互位置Fig.5 Mutual position of aircrafts at 6 000 m
数据分析、修正及实例验证表明:在爬升穿越高度层前,与相邻逆向高度层反向飞行的飞机要满足125 km的间隔(起始高度非8 400 m);当起始高度为8 400 m时,则需要满足140 km的间隔;与相邻同向高度层上同向飞行的前后2架飞机均要满足30 km的间隔。
图6 6 300 m时飞机相互位置Fig.6 Mutual position of aircrafts at 6 300 m
4 结语
通过对几种典型机型在不同起飞重量下、不同高度层上爬升穿越前所需间隔进行计算并分析,确定了飞机在航路飞行时的最佳爬升时机,为管制员指挥航空器穿越爬升提供了决策依据,提高了管制员工作效率,加速了空中交通流量,结论可用于容量评估及空域规划研究。
[1]THIPPHAVONG D.Analysis of Climb Trajectory Modeling for Separation Assurance Automation[C]//AIAA Guidance,Navigation,and Control(GNC)Conference,Honolulu,Hawaii:August 18-21,2008.
[2]REICH P G.Analysis of long-range air traffic systems:separation standards-I[J].Journal of Navigation,1966,19(1):88-98.
[3]BROOKER P.Lateral collision risk in air traffic track systems:A‘Post-Reich’event model[J].The Journal of Navigation,2003,56(3):399-409.
[4]BROOKER P.Longitudinal collision risk for ATC track systems:a hazardous event model[J].Journal of Navigation,2006,59(1):55-70.
[5]张兆宁,张晓燕,李冬宾.基于VOR导航的平行航路侧向碰撞率计算模型[J].交通运输工程学报,2007,7(3):21-24.
[6]张 勇,郝 兵,杨晓嘉.相邻高度层上穿越飞行中纵向间隔的评估[J].中国民航飞行学院学报,2010,21(6):7-12.
[7]王 玉,谷润平.飞机最佳爬升速度计算与研究[J].中国民航飞行学院学报,2008,19(1):31-33.
[8]傅职忠.航路爬升性能计算[J].中国民航学院学报,1991,9(2):26-38.
(责任编辑:党亚茹)
Research on optimal en-route climbing opportunity
DAI Jun1,WANG Jian1,WANG Yong2,LI Sheng1
(1.North China Air Traffic Management Bureau of CAAC,Beijing 100621,China;2.Tianjin Air Traffic Management Sub-bureau of CAAC,Tianjin 300300,China)
It is significant to confirm the optimal en-route climbing opportunity for flight safety and efficiency improvement. Take the crossing separation standard of Beijing control area as an example,aircrafts'required longitudinal separations before crossing flight levels are calculated by programming according to several typical models of aircrafts,takeoff weights,flight levels and other relevant factors,then the separations are corrected by considering speed change of aircrafts and the optimal opportunity for en-route climbing is defined.The result improves ATC's work efficiency and increases air traffic flow;meanwhile,it is worthwhile for capacity evaluation and airspace planning.
en-route climb;flight safety;separation standard;air traffic flow
V355;U8
:A
:1674-5590(2014)05-0027-04
2014-03-14;
:2014-04-24
戴 军(1966—),男,江西安义人,工程师,硕士,研究方向为空中交通管理.
