平面阵子阵级自适应波束形成方法研究

(中国人民解放军装备学院,北京101416)

0 引言

阵列天线一般由多个阵元按照一定的排列规则组合而成,通过调整各个阵元的相位与幅度,可使整个阵列形成期望的方向图,以达到增强期望信号抑制无用信号的目的。常见的阵列天线形式有线阵、平面阵、球面阵以及共形阵等,其中又以平面阵天线的应用最为广泛。数字波束形成(DBF)技术通过直接对基带数字信号进行的加权运算形成期望波束,省去了传统天线中的射频衰减器和移相器,降低了设备成本与复杂度,使波束形成更加快捷。对自适应数字波束形成(ADBF)方法的研究多是基于阵元级,也就是全自适应波束形成。对于阵元数目不太大的小型阵列天线来说,阵元级ADBF方法尚可行,若天线阵元数目较大,ADBF算法需要处理的数据很大,将给波束形成算法实现以及实时性等带来巨大困难。

对于大型阵列天线,子阵级自适应处理方法不仅运算量小,收敛速度快,系统硬件设备少,而且有可能逼近全自适应处理的性能。子阵划分是有效实施子阵级ADBF的基础,不同的子阵划分形式其自适应波束形成性能差别很大。平面阵子阵划分需要同时考虑行和列二维子阵划分,相对线阵的子阵划分更加复杂。对平面阵最优子阵的求解方法可归结为两种方式：一是通过智能算法寻找全局最优解,如遗传算法[1-2]、粒子群算法[3-4]等;二是对参考权值的聚类划分方法[5]。其中,文献[1]中固定行方向子阵划分,采用GA优化列向量子阵分均匀划分且上下浮动,在期望区域内得到主旁瓣比的波束方向图。文献[3]在此基础上,采用粒子群算法对行列同时进行非均匀子阵划分,进一步减少了子阵的数目。文献[5]提出了一种权矢量逼近准则线的聚类划分方法,提高了波束形成性能。文献[6-7]对子阵级权值进行归一化,使各个子阵级噪声电平相等达到降低旁瓣电平的目的。

虽然上述子阵划分方法不尽相同,波束形成性能各有优劣,但子阵结构应满足：系统自由度满足应用需求;栅瓣效应的影响尽可能小;主旁瓣电平比尽可能高。本文在上述子阵划分原则的基础上,采用遗传算法将平面阵进行两级子阵划分,进一步降低了栅瓣的影响;针对非均匀子阵结构各子阵通道噪声功率不同,导致自适应波束形成性能的下降的问题。本文通过对阵列协方差矩阵进行奇异值分解、重构特征子空间实现子阵级ADBF,提高子阵级波束形成性能。

1 阵列模型

图1示意一个M×N阵元的矩形平面阵结构。整个阵面位于xoz平面,阵元间距为d,设参考点阵元(0,0)接收到(θ,φ)方向的信号为s(t)=p0e-jωt,p0为信号强度,θ与φ分别表示来波信号方向的方位角和俯仰角。则阵元(m,n)接收信号可表示为

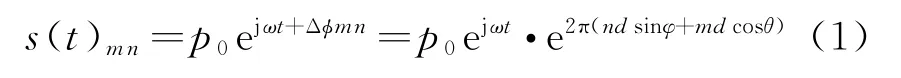
式中,Δφmn=2π(ndsinφ+mdcosφsinθ)/λ为阵元(m,n)与参考阵元接收信号的相位差。整个阵列的接收信号可表示为

图1 平面阵结构示意图

由于各阵元接收信号存在相位差,导致叠加后整个阵列的输出信号增益不能得到有效增强,因此需要对各阵元接收信号进行相位补偿。为了让阵列天线方向图指向(φ0,θ0),各阵元补偿相位ψmn应为

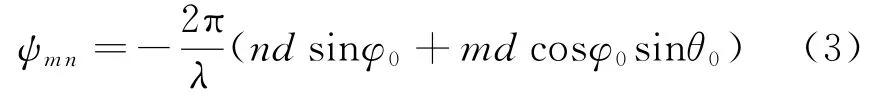
经阵元相位加权以后,阵列输出信号为

阵列天线方向图为

可将上式写成矩阵形式

式中,

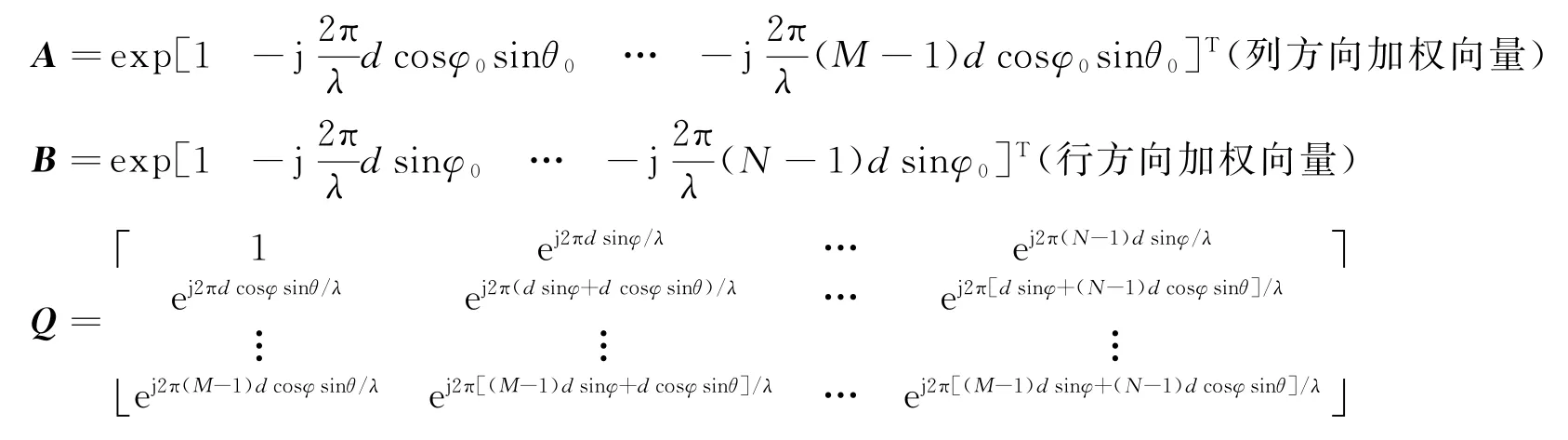
需要注意的是,这里只进行了相位加权,没有进行幅度加权。相位加权仅使天线的主瓣对准目标,没有实现对不同来向的干扰进行抑制。如果强干扰进入天线旁瓣同样会严重影响天线的接收效果,通过对阵元接收信号进行复加权,既实现了相位校正,也进行了幅度的校正。在一定的自适应准则下,阵列天线进行自适应加权处理后,不仅可使主瓣对准期望信号,且在干扰方向形成零陷。若各阵元复加权Ωmn=ωmnexp[2π(ndsinφ+mdcosφsinθ)/λ],其中ωmn表示阵元(m,n)幅度加权,则阵列方向图为

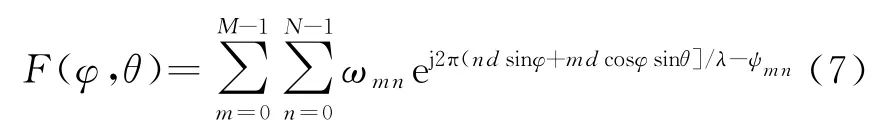
2 平面阵子阵划分方法

2.1 基于GA的平面阵子阵划分方法

子阵划分是子阵级自适应波束形成的基础,不同子阵划分结构影响着阵列波束形成性能。均匀子阵划分方法简单、便于实现,但是子阵间间距呈周期性分布,因此容易导致严重的栅瓣效应。子阵的非均匀划分可以在一定程度上抑制栅瓣效应,与线阵的子阵划分不同,在对平面阵进行子阵划分时需要同时考虑二维阵列方向上的划分形式。

GA是借鉴生物在自然界中的遗传和进化过程而形成一种全局概率搜索算法。它具有简单通用、鲁棒性强、适于并行处理、尤其适用于解决传统搜索方法难以解决的复杂和非线性问题。GA最早由Holland在1975年提出,此后GA被广泛应用于各个领域。在阵列天线中最初用于波束形成、低旁瓣天线设计以及天线自适应调零[8-10]。

结合应用实际,基于GA的邻接非重叠子阵划分的基本流程如图2所示。确定种群规模、变异概率等参数,由任意初始种群开始,对阵列划分进行编码,通过随机选择、交叉和变异等遗传操作,解码并评判个体,判断是否满足准则,否则重复上述操作。

适应度函数用来评价每个染色体的优劣。优化子阵划分的目的是抑制子阵级波束形成的栅瓣效应,因此,将主瓣与最大旁瓣电平的比值作为适应度函数,使旁瓣相对电平最小化。适应度函数f(K,M k)=max[min(MSR(K,M k))],其中,K为划分子阵数目,M k为第k个子阵包含的阵元数。对于阵元总数一定的阵列,为了避免交叉后导致阵元数目变化,在交叉中引入约束条件,即参与交叉的基因不会改变原染色体所对应的阵元数目。

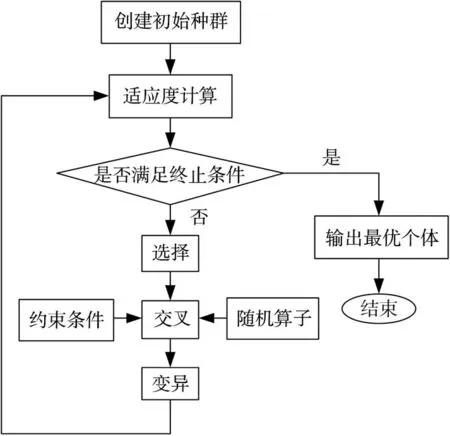
图2 GA基本流程图

2.2 平面阵不同子阵划分结构

考虑将一个40×50个阵元的平面阵划分为6×8个子阵,分析不同的行列划分形式对波束形成性能的影响。子阵划分对阵列方向图的影响,主要表现在子阵级方向图存在明显的栅瓣效应。尽可能地抑制栅瓣效应,提高方向图的主旁瓣电平比是判断子阵划分优劣的一个重要依据。

虽然均匀平面子阵结构简单、易于实现,但是由存在严重的栅瓣效应。并且会随着子阵间距的增加旁瓣越来越靠近主瓣,导致阵列天线主旁瓣性能急剧恶化。图3是将上述平面进行均匀子阵划分,当主瓣指向(0°,0°)时的子阵级方向图。

可以看出,对于均匀子阵结构的平面阵,不论是方位方向还是俯仰方向上,都存在严重的栅瓣。这是由于均匀子阵结构子阵间距较大且呈周期性排列造成的,采用GA算法对平面阵进行非均匀子阵划分,可以打破这种造成高电平栅瓣的阵列周期性。

平面子阵结构Ⅰ：列方向上GA非均匀划分结构,而后对每一个子列阵元内采用GA方法划分为非均匀结构。当期望主瓣指向(0°,0°)时,整个阵列的子阵划分形式如图4所示,图5是与之对应的子阵波束方向图。

与图3均匀平面子阵结构相比,栅瓣被明显削弱,但是由于每一子列内各子阵相位中心的横坐标相同,导致波束方向图在方位方向旁瓣仍较高。

平面子阵结构Ⅱ：采用两级子阵划分方法,在子阵结构Ⅰ的基础上,对每一列内子阵相位中心的横坐标进行非均匀规划。第一级子阵划分将整个阵列分为均匀四个象限,每个象限内采用子阵结构Ⅰ的划分方法。通过两级子阵划分,进一步破坏了各子阵相位中心排列的规律性,抑制俯仰与方位二维方向的高旁瓣。两级子阵划分后阵列结构如图6所示,图7是与之对应的子阵波束方向图。

图3 均匀平面子阵结构子阵方向图

图4 平面子阵结构Ⅰ

图5 平面子阵结构Ⅰ对应的子阵方向图

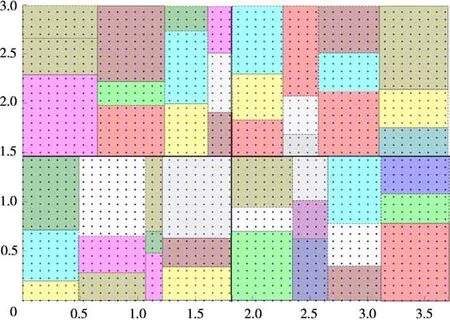
图6 平面子阵结构Ⅱ

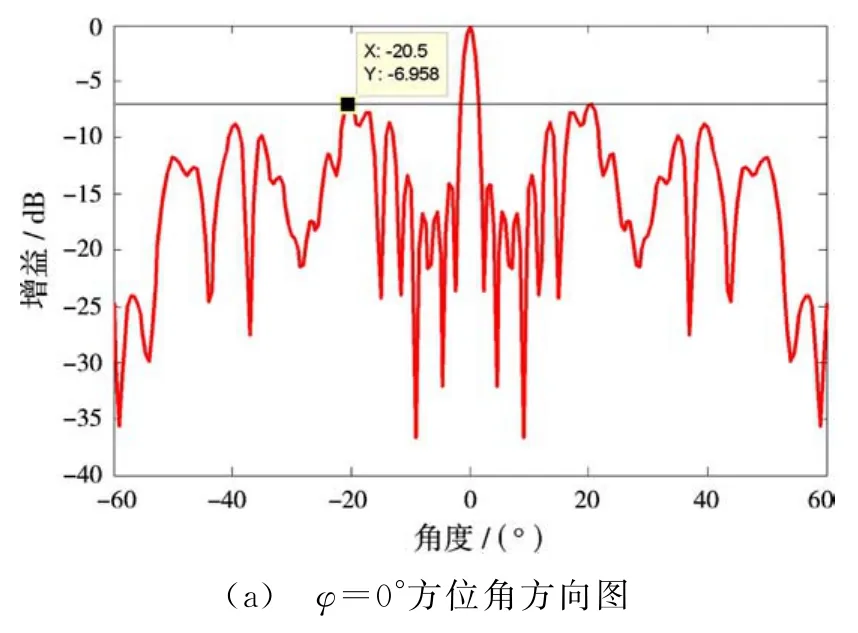
图7 平面子阵结构Ⅱ对应的子阵方向图

由图7可以看出,经过两级子阵划分以后,整个阵列的周期性被进一步破坏,旁瓣电平得到了进一步的抑制。与平面阵列结构Ⅰ相比,虽然平面阵列结构Ⅱ在方位上旁瓣电平改善并不明显,但其在方位上主旁瓣电平比提高了1.5 d B。

3 平面阵子阵级ADBF

3.1 基于特征空间的ADBF方法

子阵级ADBF一个显著的优点就是在阵元级加权值不变时,仅通过调整子阵级权值即可使阵列形成期望波束形状。子阵级波束形成直接处理数据来源于各子阵的输出,因此需要将阵元接收到的快拍数据转换到子阵级。假设在一定的角度范围内,阵元级加权值向量不变。若将M×N的平面阵划分成P×Q个子阵,则阵元接收数据X与各子阵输出数据Y的矩阵表示形式为

阵列子阵输出与阵元接收信号之间的关系为

将上式简写为

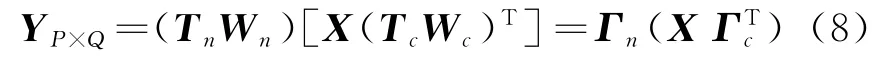
式中,Γn=T n W n,Γc=T c W c;W n=diag[exp(-j2π(m-1)cosφ0sinθ0/λ)]m=0,…,M-1,W c=diag[exp(-j2π(n-1)sinφ0/λ)]m=0,…,N-1,分别为行方向上的加权与列方向上的加权;T n表示P×M的行子阵生成矩阵,其第p行中只有与第p列子阵中阵元相对应的位置为1,其余均为0;T c表示Q×N的行子阵生成矩阵,其第q行中只有与第q列子阵中阵元相对应的位置为1,其余均为0。

考虑采用最小方差无失真响应(MVDR,minimum variance distortionless response)算法,经自适应加权后,接收到的期望信号无失真,且阵列天线输出方差最小。子阵加权值应是满足下面极值方程的解

式中,Rsub为子阵级协方差矩阵,asub(θ0)=Γn a(θ0)Γc表示子阵级期望信号方向矢量。运用拉格朗日法,引入系数μ将方差与约束条件合并,构成二次函数形式的代价函数,当梯度等于零可以求得代价函数的最小值。

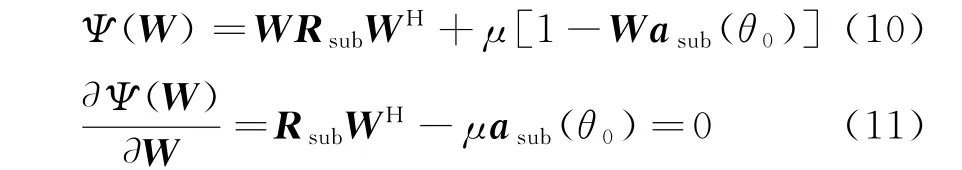
可得最佳权向量

下面求系数μ,可将式(12)等号两边左乘以,得

根据约束条件Wasub(θ0)=1,故可得

将μ代入式(12),可得子阵级ADBF的自适应权向量为

上式在Rsub为干扰和噪声相关矩阵时得到子阵级最优权系数。在实际中,干扰与噪声的相关矩阵无法直接得到,只能通过有限次阵列快拍数据估计得到。阵列接收数据中包含期望信号、干扰信号和噪声三部分,因此实际Rsub是包含期望信号与非期望信号的相关矩阵的估计值。此外,由于子阵非均匀划分结构,各子阵输出数据中包含的噪声功率并不相等,将导致自适应算法性能严重下降。可见,子阵级噪声功率不一致、快拍数、期望信号都会对自适应波束形成性能造成影响。

通过对阵列特征空间的重构可有效消除子阵噪声功率不一致到自适应波束形成的影响。首先利用阵列数据矩阵的SVD分解,可以直接从数据矩阵获得协方差矩阵的特征值和特征向量;再分解特征子空间,并对信号和噪声子空间重置,重构子阵级协方差矩阵;最后直接利用奇异值分解的子空间计算自适应权向量。因此,可以避免矩阵求逆运算,减小运算量和估计误差,消除子空间不完全正交以及协方差矩阵估计误差等对波束形成的影响。

对子阵级协方差矩阵进行SVD分解,可得

式中,S=diag[λk],k=1,2,…,K。假设阵列数据中包含一个期望信号,J个干扰,一个高斯白噪声,理想条件下,S应是秩为J的对角阵。由于期望信号的存在以及子阵噪声的不一致,导致S为满秩对角阵。用低秩对角阵S′代替满秩阵S,重构子阵协方差矩阵,即

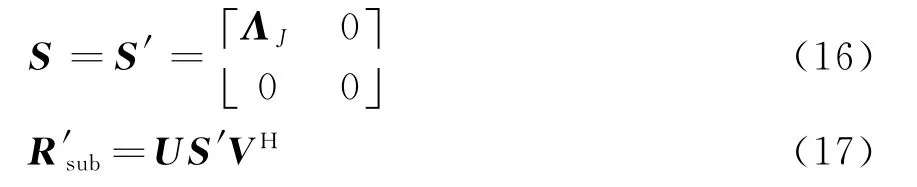
子阵特征空间重构的实质就是用重构子阵协方差矩阵重构后的子阵协方差矩阵代替常规估计协方差矩阵。直接利用信号和干扰噪声子空间完成自适应波束形成,避免了矩阵求逆运算,消除了子阵噪声不一致对阵列方向图的影响。

3.2 仿真验证

采用平面子阵结构Ⅱ,设期望目标方向为(0°,15°),干扰方向为 (2°,12°),INR=30 dB,SNR=0 d B,快拍数M=300,得到平面阵子阵级自适应波束形成方向图如图8和图9所示。

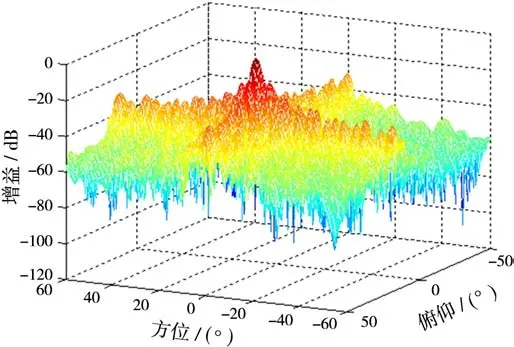
图8 特征空间重构法ADBF三维方向图

图9 常规法ADBF三维方向图

由图8和图9可以看出,特征空间重构法具有更优主旁瓣电平性能,这是由于通过对平面阵子阵特征空间的重构,消除了非均匀子阵划分带来的各子阵通道噪声功率不一致对ADBF算法的影响。图10是图8中主瓣临近区域的局部放大,可见该算法在期望目标方向形成主波束,并且在干扰方向(2°,12°)及其邻近区域形成了-80 dB的凹陷,可以达到抑制干扰的效果。

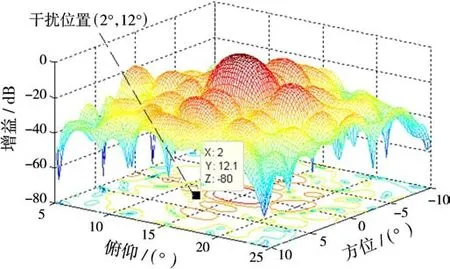
图10 空间重构法ADBF三维方向图

4 结束语

本文采用遗传算法对大型平面阵进行非均匀子阵划分,为进一步抑制旁瓣电平,采用两级子阵划分结构,使平面阵在方位和俯仰方向都具有较好的主旁瓣电平性能;由于平面阵的非均匀划分,带来各子阵噪声功率的不一致,导致子阵级自适应波束形成算法性能严重下降。采用平面子阵特征空间重构法,可有效提高子阵ADBF算法性能。本文介绍的大型平面阵子阵划分及其自适应形成方法,可为大型平面阵天线在多目标测控领域的研究与应用提供参考。但本文仅讨论了平面阵子阵级ADBF,实际应用中,为了获得更好的覆盖性能,充分利用天线载体的几何特性,共形天线的子阵级ADBF是下一步研究的重点。

[1]WANG H,FANG D G,CHOW Y L.Grating Lobe Reduction in a Phased Array of Limited Scanning[J].IEEE Trans on Antennas and Propagation,2008,56(6)：1581-1586.

[2]董晔,李瑞,李晓明.二维面阵子阵划分及PADBF算法研究[J].计算机仿真,2012,29(7)：14-18.

[3]王文昌,李雷,刘春静,等.基于粒子群优化算法的非均匀子阵波束形成技术[J].电子信息对抗技术,2010,25(1)：36-40.

[4]熊子源,徐振海,张亮.基于聚类算法的最优子阵划分方法研究[J].电子学报,2011,39(11)：2615-2621.

[5]张增辉,胡卫东,郁文贤.遗传二进制多粒子群优化算法及其在子阵STAP中的应用[J].信号处理,2009,25(1)：52-57.

[6]张旭红,李会勇,何子述.平面数字阵列雷达的子阵级波束形成算法[J].雷达科学与技术,2008,6(6)：440-444.ZHANG Xu-hong,LI Hui-yong,HE Zi-shu.Beamforming Algorithm at Subarray Level for Planar Digital Array Radar[J].Radar Science and Technology,2008,6(6)：440-444.(in Chinese)

[7]HU H,DENG X H.An Improved LCMV Method at Subarray Level[C]∥IEEE International Conference on Wireless,Mobile and Multimedia Networks,Hangzhou,China：[s.n.],2006：1-4.

[8]CAORSI S,LOMMI A,MASSA A,et al.Peak Sidelobe Level Reduction with a Hybrid Approach Based on GA and Difference Sets[J].IEEE Trans on Antennas and Propagation,2004,52(4)：1116-1121.

[9]WEILE D S,MICHIELSSEN E,The Control of Adaptive Antenna Arrays with Genetic Algorithms Using Dominance and Diploidy[J].IEEE Trans on Antennas and Propagation,2001,49(10)：1424-1433.

[10]YALLAPARAGADA N T,HARDEL G R,MANDAL D,et al.Genetic Algorithm for Null Synthesizing of Circular Array Antennas by Amplitude Control[C]∥2011 IEEE Symposium on Computers&Informatics,Kuala Lumpur：[s.n.],2011：1-5.