箱梁合龙段底板崩裂机理及设计

张 峰 叶见曙 高 磊

(1 山东大学岩土与结构工程研究中心，济南250061)

(2 东南大学交通学院，南京210096)

随着连续刚构桥跨径的不断增大，跨中下挠及箱梁开裂问题越来越突出［1-2］.为了克服这些问题，通常采用增加跨中底板预应力束的方式弥补.但由于设计者对预应力束的作用效应认识不足，引发了一些工程问题，如预应力张拉后箱梁底板混凝土崩裂破坏.冯鹏程等［3］研究箱梁底板崩裂时仅考虑了弹性计算，未讨论底板开始出现损伤后的发展趋势.Zuo 等［4-5］对箱梁底板崩裂进行了三维非线性分析，但是底板网格只分了3 层，无法有效描述底板破坏的发展情况.项贻强等［6-7］基于非线性分析模型，分析了箱梁底板合龙段预应力束张拉后裂缝的扩展，并认为受合龙束孔道的影响，孔肋为受力最不利区域，在径向力作用下，孔肋的斜裂缝和撕裂裂缝是导致箱梁破坏的主要原因;在今后箱梁设计中，底板横向除应满足抗剪承载力外，孔肋尚需满足最小孔道间距的要求.上述研究仅针对竖向一排波纹孔道进行了分析.重载铁路连续刚构桥中预应力束用量较大，跨中合龙段底板竖向通常布置双层波纹孔道，故箱梁底板的崩裂机理更为复杂.

为进一步揭示包含双层波纹孔道的箱梁底板崩裂机理，本文基于精细化数值模拟、现场崩裂图片及混凝土非线性力学，研究了箱梁底板崩裂成因及其出现的先后顺序，并提出了对应的设计公式.

1 箱梁底板崩裂破坏形态

对多座箱梁合龙段底板崩裂的照片进行破坏分类，具体参见图1.可见，箱梁底板崩裂后的局部破坏形态可分为以下4 种:①波纹管孔肋间竖向受拉裂缝;②混凝土与波纹管的剥离;③跨越波纹孔道的斜裂缝;④孔肋间混凝土顶、底部裂缝.

图1 已有箱梁合龙段底板崩裂照片

2 计算模型

2.1 背景桥梁

所用桥梁为跨径布置70 m +3 ×120 m +70 m的五跨预应力混凝土刚构连续梁桥，合龙段长2 m，桥梁立面图见图2.中跨底板布置30 束合龙束，合龙束采用17-φj15.2 钢绞线.

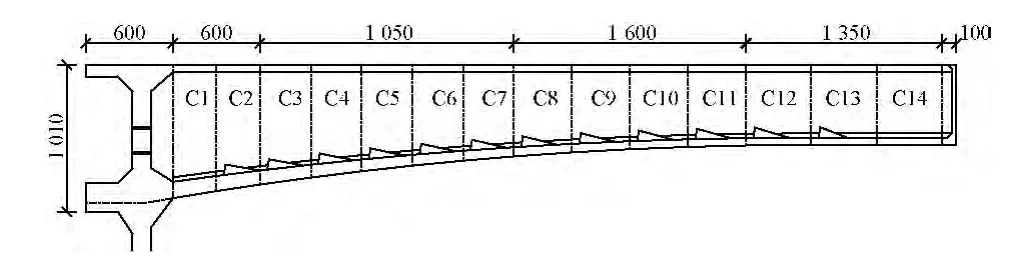
图2 桥梁立面图(单位:cm)

取预应力筋微单元，参考图3进行分析，可得张拉预应力筋产生的对腹板或底板的径向压力q(x)为

式中，Npe为预应力筋张拉力;R 为预应力筋曲线近似按圆弧线处理的圆弧半径;L 为合龙段长度;h为合龙段两端的高差;x 为跨径方向距离底板变厚点的距离;b 为假定预应力筋圆弧线为抛物线y=axb时的方程幂次;y 为底板高差.

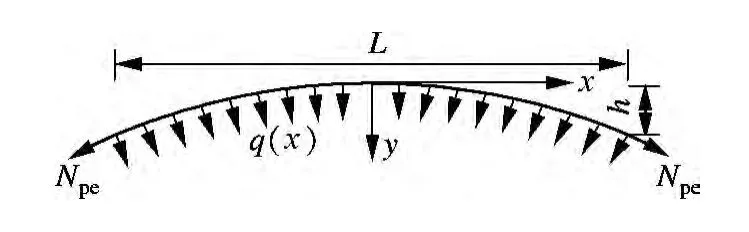
图3 等效预应力计算模型

对中跨底板进行统计分析，得到如图4所示的底板形状拟合曲线.

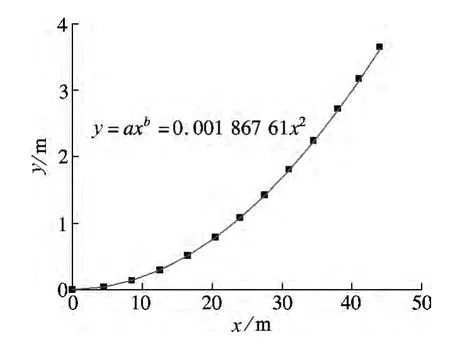
图4 底板形状参数拟合曲线

2.2 精细化数值模型

借鉴平面框架法的思想，取跨中截面单位梁段建模，考虑到结构的对称性，采用1/2 模型进行计算(见图5(a)).采用Abaqus 软件进行模拟分析，底板单元边长为0.01 m，混凝土采用二维四节点等参元CPE4，钢筋采用杆单元T2D2 模拟.模型中考虑了竖向预应力钢筋及普通受力钢筋的建模(见图5(b)).在波纹孔道内部施加向下的作用力Pu，根据设计文件，所有钢束同步张拉，在每个孔道内施加22.391 kN 的作用力，作用力布置参见图5(c).

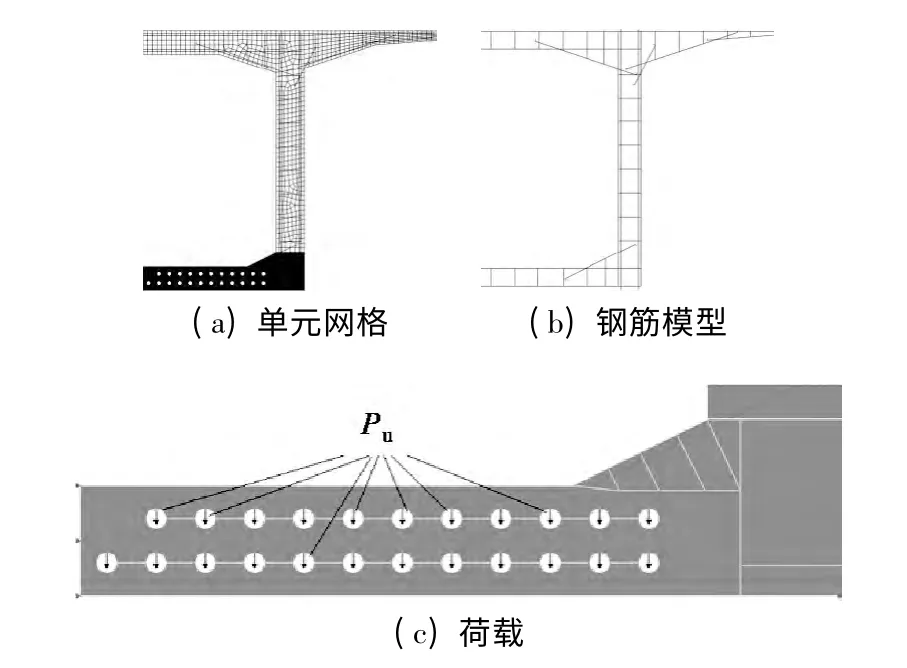
图5 有限元模型

2.3 材料本构

混凝土材料的单轴受压全应力-应变曲线采用Saenz 公式［8］，即

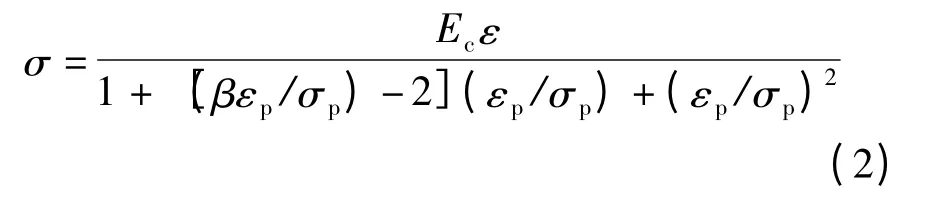
式中，σ 为混凝土应力;ε 为混凝土应变;εp为峰值混凝土应力对应的应变;σp为混凝土峰值应力;β为初始切线模量的实验确定系数;Ec为混凝土弹性模量.

混凝土材料的单轴受拉全应力-裂缝宽度曲线采用Hordijk 公式［8］，即

式中，wt为混凝土裂缝开裂宽度;wcr为混凝土开裂后拉应力完全释放时对应的裂缝宽度;σt为裂缝垂直方向的混凝土拉应力;ft为混凝土抗拉强度;GF为混凝土断裂能;c1=3.0，c2=6.93.如果无实测资料，ft与GF可基于CEB-FIP 公式计算，即

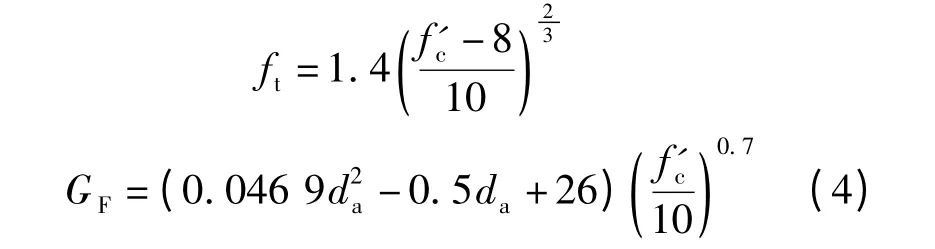
式中，da为最大骨料尺寸;f'c为混凝土圆柱体抗压强度.

2.4 裂缝模型

采用钝带裂缝模型进行计算，裂缝宽度wt可采用混凝土开裂应变εcr在裂缝带宽Lcr内积分获得，即

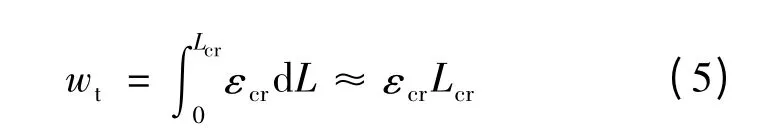
裂缝带宽Lcr可采用单元变长计算［9］.由式(5)可看出，在相同开裂应变条件下，单元越小，裂缝宽度越小，应力下降越慢，由此便可有效降低单元尺寸效应的影响.混凝土采用塑性损伤模型，其混凝土强度准则及损伤计算公式参见文献［9］.

3 箱梁底板崩裂机理

为便于描述，定义加载荷载为kPu，其中k 为荷载因子.图6为不同荷载步下第一主应力s1分布情况.

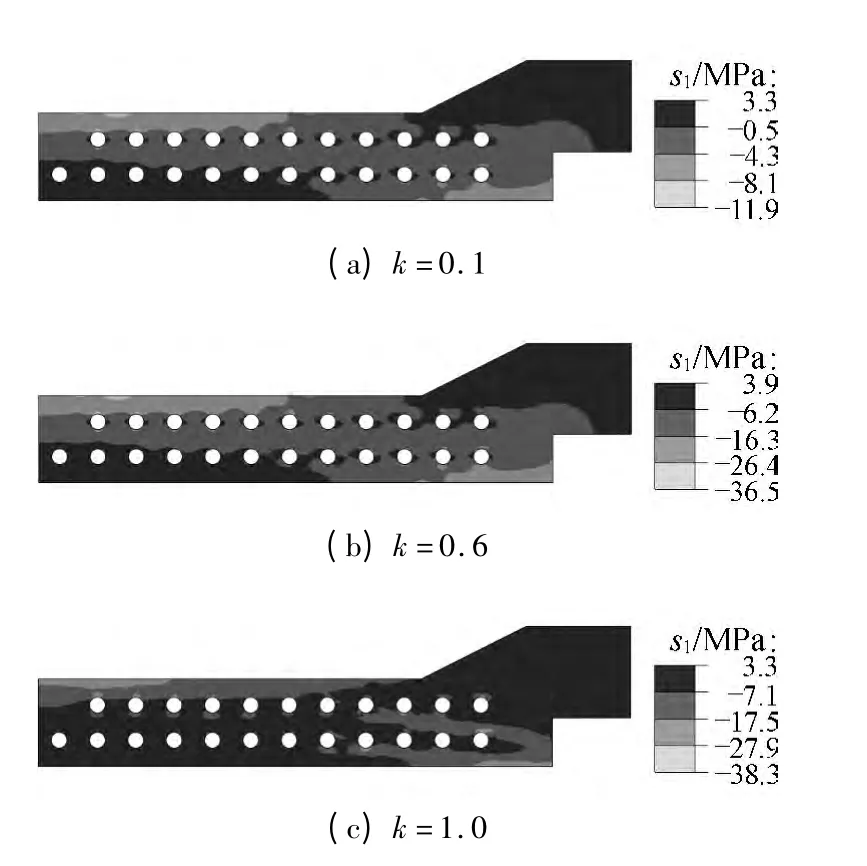
图6 不同荷载步下第一主应力分布情况

由图6可知，径向力施加后，底板正弯矩区域及靠近腹板区域的混凝土主拉应力较其余位置要大.底板波纹管孔肋竖向中间位置出现了较大的拉应力，该拉应力会导致箱梁底板发生上下两层的剥离(见图1(a)和(c)).

图7为底板崩裂过程中混凝土裂缝的扩展情况.由图可知，当k=0.3 时，梗腋位置发生了剪拉裂缝，破坏后期该裂缝在底板梗腋部位演变为宏观剪切裂缝(k=1.0)，导致箱梁底板完全丧失承载能力.因此，底板横向抗剪验算可以选取图7(h)中所示截面开展.底板横向中间底部位置出现典型的竖向弯曲裂缝.

当k=0.5 时，出现波纹管肋间竖向受拉裂缝(见图7(d)).同时，混凝土与波纹孔道之间的黏结力增大，该黏结力失效后则出现波纹管与混凝土之间的剥离破坏(见图1(b)).当k=0.5 时，波纹管下方出现了混凝土冲切破坏(见图7(e)).

当k=0.9 时，梗腋位置附近的波纹管出现了典型的横向裂缝，该现象与图1(d)一致.

综合分析裂缝扩展结果表明，对于竖向双层的波纹孔道，冲切破坏仅在下层发生;孔肋间的竖向受拉破坏则在上下两层均会发生.

由此可知，混凝土箱梁底板的崩裂成因可分为2 大类:局部破坏和宏观破坏.

局部破坏包括:①竖向受拉破坏，即预应力孔道在向下的荷载作用下于孔肋间产生破坏.②混凝土冲切破坏，即下层孔道往下挤压下方的混凝土，以近似45°扩散并产生棱柱体破坏形态.③孔肋顶、底部横向崩裂破坏，即波纹孔道顶、底面出现了较大了横向剪力，该剪力导致此破坏形态.④波纹管与混凝土的剥离破坏，即波纹管与混凝土的界面黏结力失效.

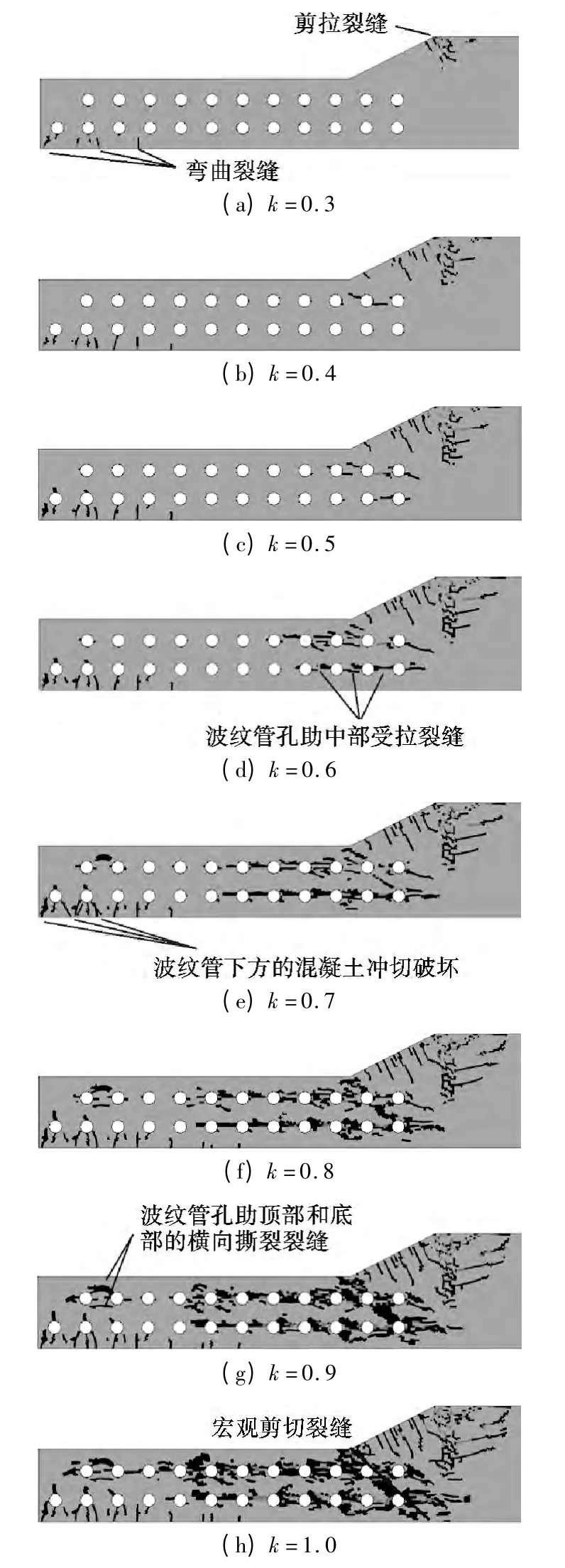
图7 不同荷载步下的底板裂缝分布

宏观破坏包括底板横向跨中位置的弯曲破坏和梗腋处的剪切破坏.底板可近似假定为两端带弹性约束支撑的梁，在跨中底部出现弯曲裂缝，在支座附近(梗腋位置)出现剪切破坏.

破坏出现的先后顺序如下:首先，出现竖向受拉裂缝和混凝土冲切破坏，同时伴随波纹管顶部与混凝土的剥离破坏.其次，发生波纹孔道间孔肋混凝土顶、底部混凝土横向崩裂破坏.最终，梗腋部位底板发生剪切破坏.

4 箱梁底板崩裂控制因素设计公式

文献［7，10］提出了不同破坏形态对应的设计公式，但是均忽略了底板钢筋对破坏时承载能力的影响.

4.1 孔肋间混凝土竖向受拉破坏

图8为孔肋间混凝土竖向受拉破坏示意图.图中，S 为水平相邻波纹管孔道中心距;d 为波纹管孔道直径;PL为竖向受拉破坏荷载.由图可以看出，如果2 个相邻的波纹管之间发生孔肋竖向受拉破坏，则每个孔道需要的径向荷载为

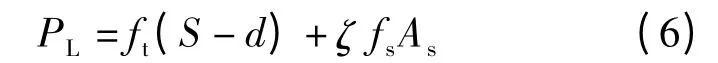
式中，ζ 为钢筋应力折减系数;fs为钢筋屈服强度;As为钢筋面积.

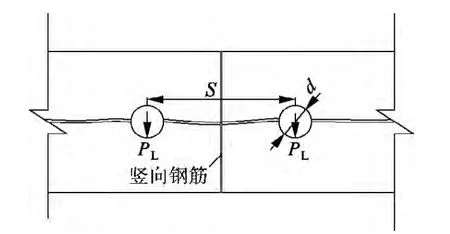
图8 孔肋间混凝土竖向受拉破坏示意图

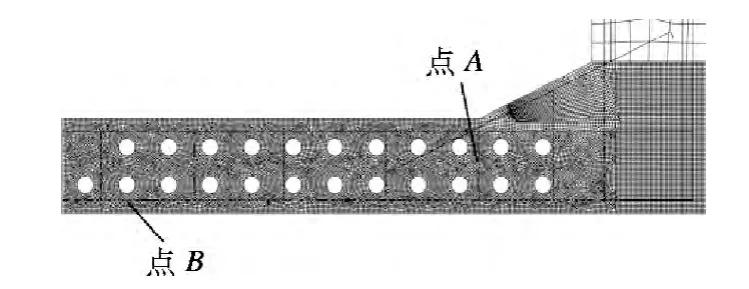
图9 钢筋应力特征点

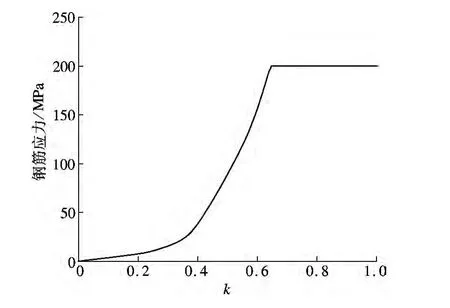
图10 点A 处钢筋应力发展情况

钢筋的应力特征点见图9.图中，点A 为孔肋间竖向受拉裂缝位置;点B 为冲切破坏位置点.图10为点A 处钢筋的应力发展情况.由图可知，当k=0.64 时，钢筋开始屈服.比较钢筋应力发展及箱梁底板裂缝发展过程，当k=0.60 时，竖向受拉钢筋和冲切破坏面中混凝土对承载能力的贡献同时达到峰值.因此，ζ 在设计中可取为1.

4.2 波纹孔道下方混凝土冲切破坏

学者们对混凝土板的冲切破坏已进行了多方面研究［11-12］.研究时将混凝土破坏形态均假定为锥体破坏，简化成轴对称问题进行分析.本文建立了柱体破坏力学分析模型(见图11(a)).图11(b)中，Ⅰ，Ⅲ为箱梁底板在径向力作用下经冲切破坏后形成的刚性区;Ⅱ为冲切破坏面;P 为钢筋混凝土板的冲切承载力;u 为沿板法向产生虚位移;δ 为冲切破坏区域Ⅱ区的厚度;n 为冲切破坏区法线方向;α2为冲切面与竖向的夹角;h0为波纹管孔道中心与底边的距离.

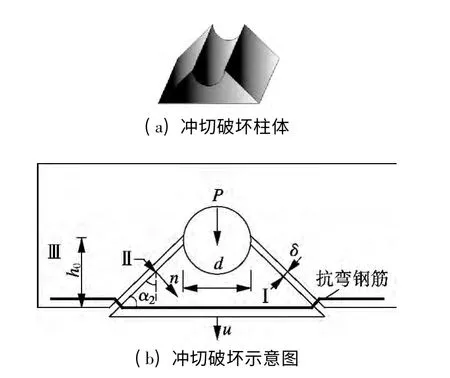
图11 箱梁底板冲切破坏

依据建立的冲切破坏模型，考虑抗弯钢筋的销栓作用.冲切承载力P 由混凝土和抗弯钢筋提供的冲切承载力Pc和Ps组成，即

基于抛物线形库仑-莫尔混凝土强度准则(见图12)对破坏锥面上的正应力和剪应力进行分析.图中，fc为混凝土轴心抗压强度;σn为破坏面上的正应力;τnt为破坏面上的剪应力;α 为包络线外法线方向与τnt轴方向的夹角.箱梁底板内某点应力可表示为(σn，τnt).抛物线形包络线的方程为

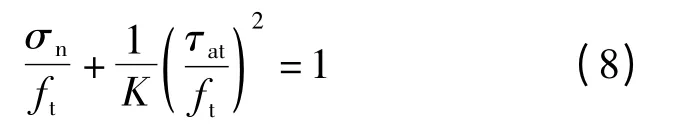
式中，K=m+2 －2 (m+1)0.5，m=fc/ft.

依据图12可得

破坏锥面上的正应力及剪应力分别为

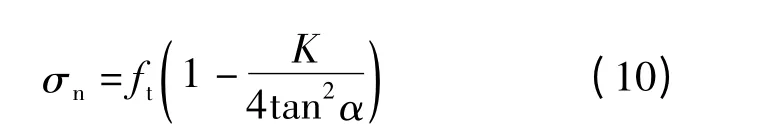
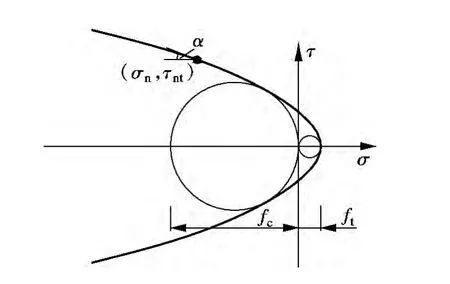
图12 抛物线形库仑-莫尔混凝土强度准则

当冲切破坏柱体Ⅰ区产生一个竖向虚位移u时，塑性区的正应变εn和剪应变γnt分别表示为

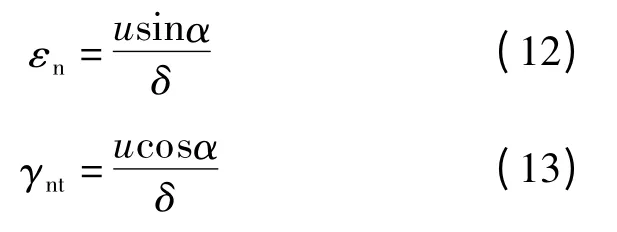
根据虚功原理，冲切破坏柱体沿垂直于板平面方向产生虚位移u 时，外荷载Pc在虚位移u 上所做的功需等于破坏柱面上总应力做的功，则

式中，M 为单侧破坏面的面积.计算M 时，按照箱梁纵向1 m 范围内进行验算，因此M=h0tanα2.

对式(14)积分可得

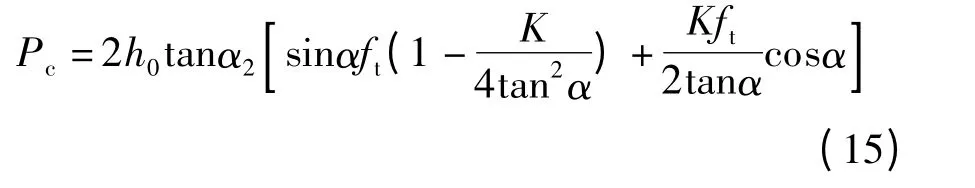
已有试验证明，混凝土板冲切破坏时箱梁底板横向钢筋可提供一定的销栓作用［11］.文献［13］采用下式计算单根钢筋销栓作用:

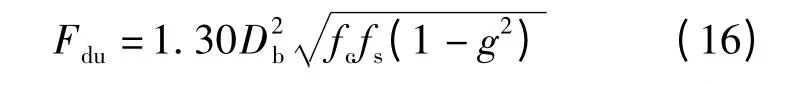
式中，Db为单根钢筋直径;fs为混凝土棱柱体抗压强度;g 为钢筋的当前应力与屈服应力的比值.钢筋的轴力如果达到屈服强度会导致销栓刚度折减，因此g≥1 时，销栓力为零.

2 个冲切面上的钢筋销栓作用表示为

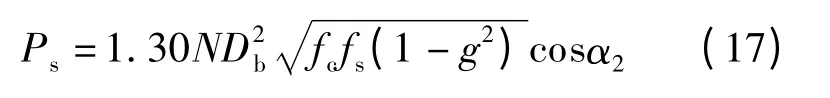
式中，N 为箱梁纵向1 m 范围内2 个冲切面范围内的横向钢筋根数.

图13为冲切破坏位置(点B)处钢筋的应力发展规律.由图可知，k=0.59 时钢筋开始屈服.分析点B 处钢筋应力发展及箱梁底板裂缝发展过程可知，当k=0.60 时，横向受拉钢筋已完全屈服，钢筋的销栓作用可以忽略不计.偏于保守设计，g 在设计中可取为1.

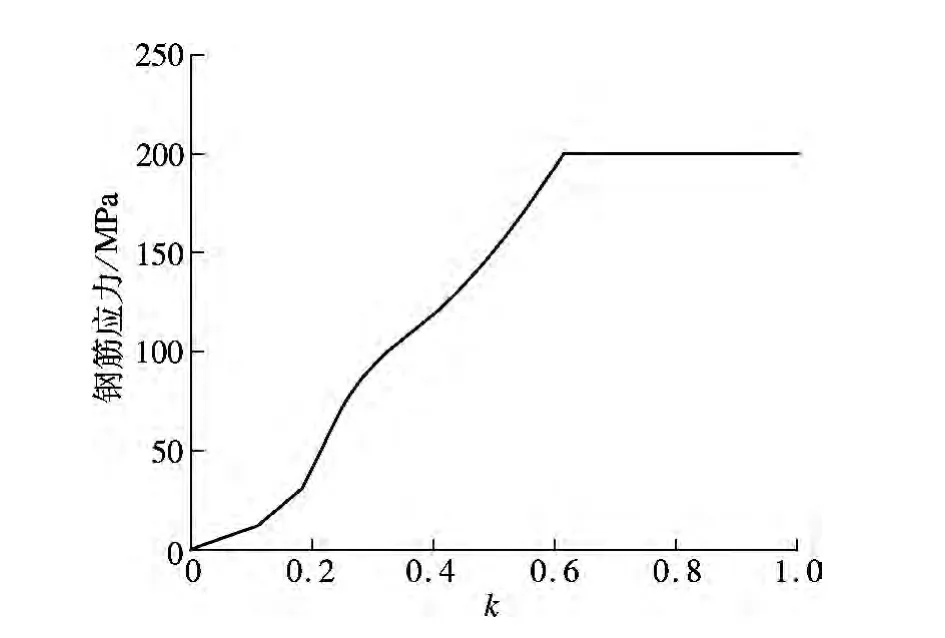
图13 点B 处钢筋应力发展

5 结论

1)混凝土箱梁底板的崩裂成因可分为局部破坏和宏观破坏2 大类.局部破坏包括孔肋间混凝土竖向受拉裂缝、波纹孔道下方混凝土冲切破坏、波纹孔道间孔肋顶和底部混凝土崩裂破坏以及波纹管与混凝土的剥离破坏.宏观破坏包括底板横向跨中位置的弯曲破坏和梗腋位置的剪切破坏.

2)对于竖向双层的波纹孔道，冲切破坏仅在下层发生;孔肋间的竖向受拉破坏则在上下两层均会发生.

3)破坏出现的先后顺序可以描述为:首先，出现孔肋间竖向受拉裂缝和混凝土冲切破坏，同时伴随波纹管与混凝土的剥离破坏;其次，发生波纹孔道间孔肋顶、底部混凝土横向剪切破坏;最终，发生宏观破坏.

4)提出了考虑箱梁底板钢筋影响的孔肋竖向受拉破坏及波纹孔道下方混凝土冲切破坏的设计公式.

5)三维应力状态下底板纵向压应力对底板崩裂的影响有待进一步研究.

References)

［1］ Bazant Z P，Yu Q，Li G H.Excessive long-time deflections of prestressed box girders.Ⅰ:record-span bridge in palau and other paradigms［J］.Journal of Structural Engineering，2012，138(6):676-686.

［2］ Bazant Z P，Yu Q，Li G H.Excessive long-time deflections of prestressed box girders.Ⅱ:numerical analysis and lessons learned［J］.Journal of Structural Engineering，2012，138(6):687-696.

［3］ 冯鹏程，吴游宇，杨耀栓，等.连续刚构底板崩裂事故的评价［J］.世界桥梁，2006(1):66-69.Feng Pengcheng，Wu Youxu，Yang Yaoshuan，et al.Analysis of accident of bursting crack in bottom slab of a continuous rigid-frame bridge［J］.World Bridges，2006(1):66-69.(in Chinese)

［4］ Zuo X D，Ge B，Song J Y.Fine analysis for bursting damage of bottom plates in closure section of continuous rigid frame bridge［J］.Advanced Materials Research，2012，594:1557-1560.

［5］ Zuo X D，Qu Z L，Ge B.Spatial effects and broken-up analysis for bottom plates of box girders in a large span rigid frame-continuous beam bridge［J］.Applied Mechanics and Materials，2012，178:2268-2272.

［6］ Xiang Y Q，Tang G B，Liu C.Cracking mechanism and simplified design method for bottom flange in prestressed concrete box girder bridge［J］.Journal of Bridge Engineering，2011，16(2):267-274.

［7］ 项贻强，唐国斌，朱汉华，等.预应力混凝土箱梁桥施工过程中底板崩裂破坏机理分析［J］.中国公路学报，2010，23(5):70-75.Xiang Yiqiang，Tang Guobin，Zhu Hanhua，et al.Failure mechanism analysis of bottom plate of prestressed concrete box girder bridge during construction［J］.China Journal of Highway and Transport，2010，23(5):70-75.(in Chinese)

［8］ Chen G M，Chen J F，Teng J G.On the finite element modeling of RC beams shear-strengthened with FRP［J］.Construction and Building Materials，2012，32:13-26.

［9］ 江见鲸，陆新征.混凝土结构有限元分析［M］.2 版.北京:清华大学出版社，2013:205-206.

［10］ 彭元诚.连续刚构箱梁底板崩裂原因分析与对策［J］.桥梁建设，2008(3):67-78.Peng Yuancheng.Cause analysis and countermeasures for bursting cracks in box girder bottom slabs of continuous rigid-frame bridge［J］.Bridge Construction，2008(3):67-78.(in Chinese)

［11］ 黄小坤，刘立渠，陶学康.考虑纵筋率及加载面边长比影响的板受冲切承载力试验研究［J］.土木工程学报，2008，41(7):21-26.Huang Xiaokun，Liu Liqu，Tao Xuekang.Experimental study on the punching shear capacity of slabs considering the influences of tension reinforcement and column aspect ratios［J］.China Civil Engineering Journal，2008，41(7):21-26.(in Chinese)

［12］ Alam J A K M，Amanat K M，Seraj S M.An experimental study on punching shear behavior of concrete slabs［J］.Advance in Structural Engineering，2009，12(2):257-265.

［13］ 张峰.预应力混凝土连续箱梁开裂后的结构行为［D］.南京:东南大学交通学院，2007.