卷边C 形截面不锈钢短柱承载力直接强度法

范圣刚 郑宝锋 刘美景 刘 芳 陶玥林

(1 东南大学混凝土与预应力混凝土教育部重点实验室，南京210096)

(2 东南大学土木工程学院，南京210096)

(3 东南大学成贤学院土木工程系，南京210088)

不锈钢作为建筑结构材料，具有造型美观、耐腐蚀性好、易于维护和全生命周期成本低等优点，在建筑结构中具有广阔的适用性.随着不锈钢产量的迅猛增长、品种的日益繁多以及加工制作水平的不断革新，在建筑市场需求的强烈驱动下，采用不锈钢作为建筑结构材料是近年来土木工程的新趋势.

卷边C 形截面不锈钢短柱是通过成品不锈钢钢板加工制作而成的构件，此类构件属于冷弯薄壁构件.目前，冷弯薄壁构件承载力的计算方法主要有2 种:有效宽度法和直接强度法.现行规范中大多采用有效宽度法.直接强度法是利用构件弹性屈曲荷载与极限荷载的关系来确定构件承载力，是确定冷弯薄壁构件承载力较为准确的一种新方法，可以方便计算带有复杂加劲截面的构件承载力.与传统的有效宽面法相比，直接强度法是以全截面特性进行承载力计算的，不需要确定构件截面的有效宽度，计算方法简单明了，处理复杂截面优势明显.

近年来，国内外学者们针对冷弯薄壁型钢构件的直接强度法开展了研究.Schafer 等［1-2］在直接强度法方面进行了大量的试验研究和理论分析，建立了受压构件与受弯构件的局部屈曲、畸变屈曲直接强度法计算公式.Lecce 等［3-4］对冷弯槽型截面不锈钢轴心受压构件的畸变屈曲性能进行了试验研究和有限元分析，提出了畸变屈曲的直接强度法公式.Becque 等［5］对C 形和I 形不锈钢构件的局部-整体相关屈曲进行了试验研究，拟合出局部-整体相关屈曲的直接强度法计算公式.刘芳等［6-7］开展了38 根奥氏体S30408 卷边C 形截面不锈钢短柱的受力性能试验研究，给出了短柱的试验破坏现象、荷载-位移曲线、转角-位移曲线以及极限承载力值.

本文针对奥氏体不锈钢材料S30408，基于直接强度法，结合已开展的38 根不锈钢短柱试验研究结果，通过有限元数值模拟和参数化分析，拟合出适用于卷边C 形截面不锈钢短柱承载力的直接强度法计算公式.

1 现有直接强度法计算公式

现有NAS 规范［8］和AS/NZS 4600—2005 规范［9］中均采用直接强度法计算构件承载力.直接强度法公式以构件截面的柔度系数λ1为变量，具体表达式如下:

轴心受压构件

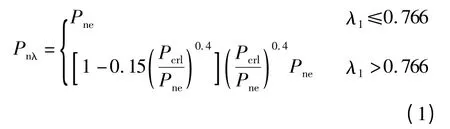
两端受弯矩作用的纯弯构件

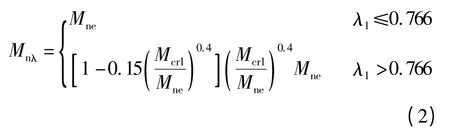
式中，Pnλ为轴心受压构件极限承载力;Pcr1为构件受压局部屈曲时的临界承载力;Pne为构件全截面有效时计算出的轴压承载力;Mnλ为纯弯构件极限弯矩值;Mcr1为纯弯构件局部屈曲时的临界弯矩值;Mne为纯弯构件全截面有效时计算出的弯矩值;λ1为构件截面(以局部屈曲为失效)的柔度系数，即构件的长细比，对于轴心受压构件有λ1=对于纯弯构件有

2 假定模型与分析模型

2.1 假定模型

根据已有的直接强度法计算公式，本文提出了适用于卷边C 形截面不锈钢短柱极限承载力的直接强度法假定模型.假定模型的具体表达式如下:

轴心受压构件

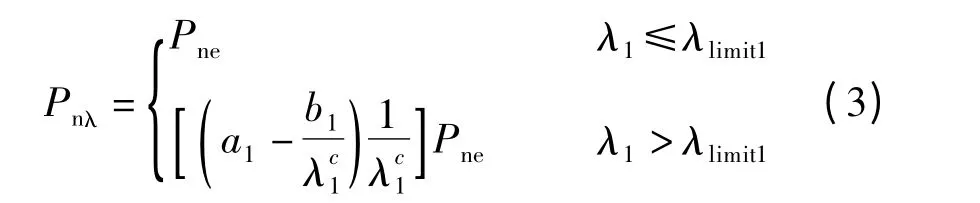
两端受弯矩作用的纯弯构件

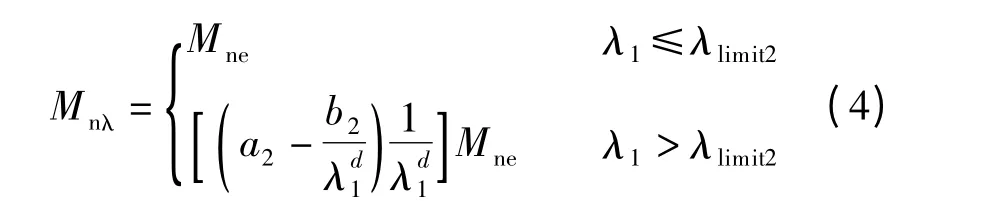
式中，a1，b1，c，λlimit1，a2，b2，d，λlimit2均为待定系数.

2.2 分析过程

为了确定卷边C 形截面不锈钢短柱承载力的准确计算公式，需通过有限元数值模拟方法拟合出式(3)和(4)中的相关待定系数.具体分析过程如下:①假定构件全截面有效，可确定出不锈钢短柱全截面有效时的轴压承载力Pne和弯矩值Mne;②利用有限条软件CUFSM 计算出构件的临界屈曲承载力Pcr和临界屈曲弯矩Mcr;③利用有限元软件ANSYS 建立准确的计算分析模型，获取不锈钢短柱的极限承载力值Pnλ和极限弯矩值Mnλ;④基于直接强度法假定模型，通过对有限元结果进行数值拟合，获取式(3)和(4)中各待定系数;⑤给出适用于卷边C 形截面不锈钢短柱极限承载力的计算公式.

2.3 分析模型

2.3.1 临界屈曲承载力

构件的临界屈曲承载力可通过有限条方法近似获取，计算分析软件为CUFSM.以截面尺寸为C80 mm ×40 mm ×15 mm ×2.0 mm 的轴心受压不锈钢短柱为例，利用CUFSM 软件求解构件临界屈曲荷载值的具体步骤如下:

①建立模型并划分单元(见图1(a)).

②施加初始荷载.对于轴心受压构件，在截面形心处施加1 kN 力作为初始荷载，截面应力分布如图1(b)所示;对于纯弯构件，沿截面中性轴施加1 kN·m 弯矩作为初始荷载.

③设置求解时间.求解时间应与划分的单元数成正比.图2为构件截面局部屈曲达到弹性临界荷载时对应的屈曲变形;构件屈曲系数与半波长度的关系曲线见图3，曲线上最小值即为临界屈曲荷载.由图可知，构件截面局部屈曲时弹性临界荷载Pcr为246.42 kN，屈曲半波长度为60.0 mm.

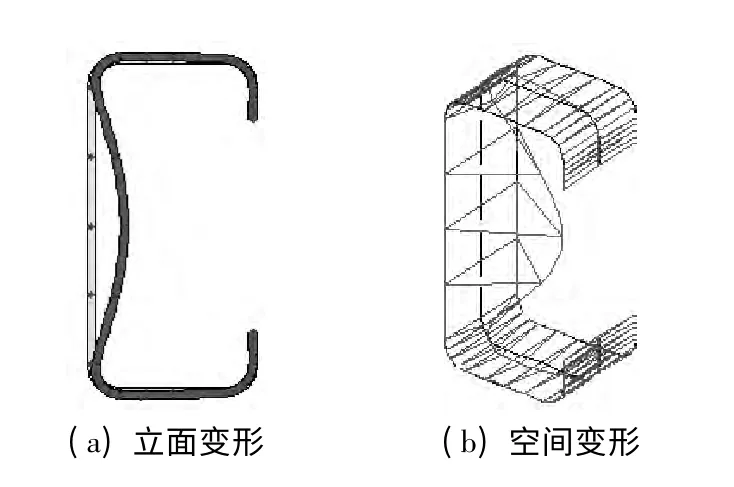
图2 局部屈曲截面变形图

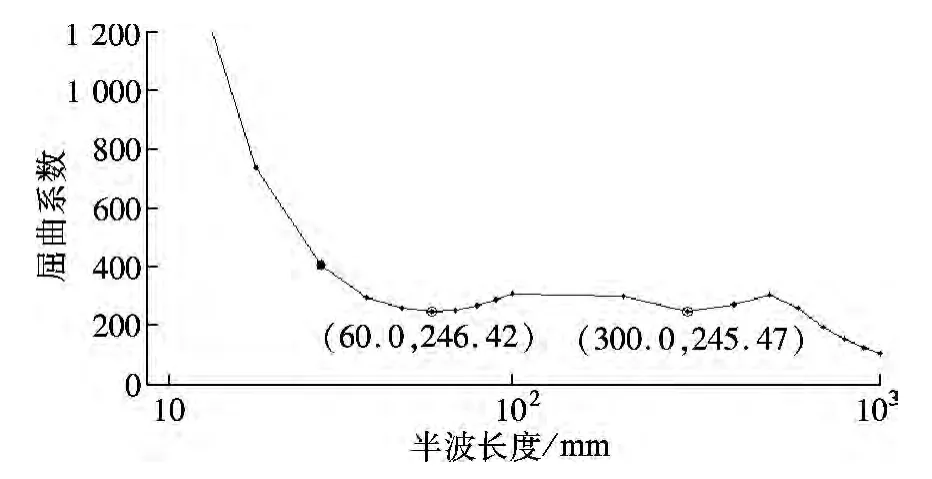
图3 屈曲系数与半波长度的关系曲线

2.3.2 极限承载力

为了准确模拟卷边C 形截面不锈钢短柱的极限承载力，本文选择了不同截面尺寸的短柱试件，通过改变试件厚度来改变截面柔度系数λ1.采用有限元软件ANSYS10.0 建立计算分析模型.通过数值模拟分析，获取不同截面尺寸和柔度系数下轴心受压构件的极限承载力值Pnλ和纯弯构件的极限弯矩值Mnλ.

1)几何模型的建立

对于大型复杂结构或节点有限元计算模型，常采用图形处理软件(CAD 或SOLIDWORKS)来建立几何模型;对简单的计算模型也可在有限元软件中直接建立几何模型.卷边C 形截面不锈钢短柱试件的计算模型较为简单，故在有限元软件中直接建立其计算模型，且考虑卷边C 形截面的转角区和卷边，几何模型如图4(a)所示.采用映射划分方法对计算模型进行网格单元划分，单元边长不超过25 mm.由于转角区范围较小，因此在计算分析模型中试件横截面上转角区仅划分1 个网格单元.计算模型的网格划分结果如图4(b)所示.

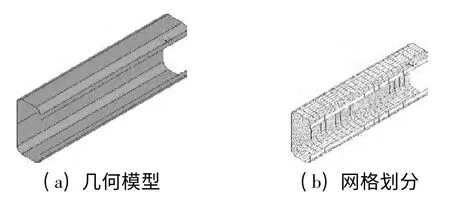
图4 有限元计算分析模型

2)计算单元的选取

对于卷边C 形截面不锈钢短柱试件，单元厚度方向的尺寸与其他2 个方向尺寸相差较大，计算单元选取Shell181 壳单元(4 节点单元，每个节点包含6 个自由度).此外，为实现端部的点加载，建立了一个质量单元Mass21(具有6 个自由度的点单元，每个坐标方向具有不同质量和转动惯量).

3)材料模型

已有的直接强度法计算公式未反映冷弯性能对转角区材料性能的影响，因此在计算分析模型中材料力学性能参数均采用平板区拉伸试验结果.基于文献［6-7］中试验结果，利用Gardner［10］提出的不锈钢材料力学性能拟合公式，构建出计算分析模型中的不锈钢材料应力-应变曲线，即

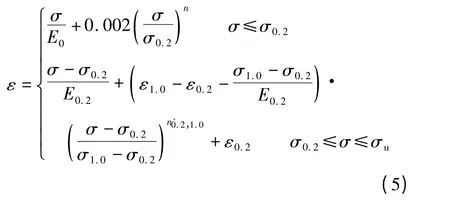
式中

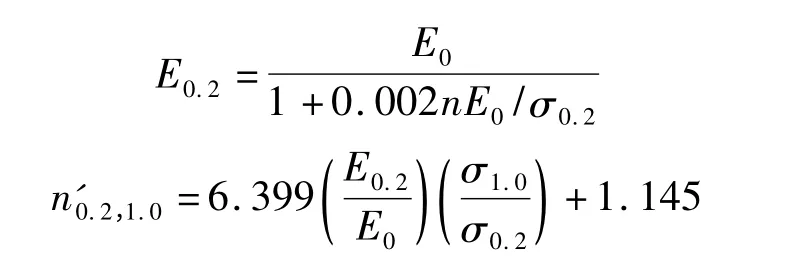
式中，E0为材料的初始弹性模量;σ0.2为材料的名义屈服应力，即残余变形值0.2%对应的应力;n=ln20/ln(σ0.2/σ0.01)为硬化指数;σ0.01为残余变形值0.01%对应的应力;σ1.0为残余变形值1.0%对应的应力;ε0.2为应力σ0.2对应的应变;ε1.0为应力σ1.0对应的应变;σu为材料的极限应力.

4)加载方式与边界条件

在计算分析模型中，采用点加载方式来模拟试件端部的加载过程.短柱下端(支承端)节点的6个自由度全部约束;短柱上端(加载端)节点除轴向自由度外其余5 个自由度全部约束，且为了使试件加载端压缩变形一致，将加载端的全部节点自由度耦合至加载点.

5)短柱试件的初始缺陷

在计算分析模型中，短柱试件的初始缺陷采用一阶弹性屈曲模态的缺陷分布模式，且利用如下的经验公式来确定缺陷的幅值［10］:

式中，ω0为缺陷的幅值;t 为短柱试件的截面厚度;σcr为卷边C 形截面的弹性屈曲应力，可采用有限条软件CUFSM 计算得到.

2.4 有限元模拟结果与试验结果对比

卷边C 形截面不锈钢短柱试验试件共包括10个轴心受压短柱和28 个偏心受压短柱［6-7］，试件的分组与截面尺寸见表1.表中，A 组试件为轴心受压短柱;B，C，D 组试件为偏心受压短柱，各偏心受压试件的偏心方向均为沿着y 轴方向(见图5).偏心后的短柱腹板应力分布可以实现以下3 种状态:①腹板两端受压，一端应力值为另一端的1/2，对应B 组;②腹板一端受压，另一端应力为零，对应C 组;③腹板一端受压，另一端受拉，其中受拉区域占总腹板高度的1/8，对应D 组.

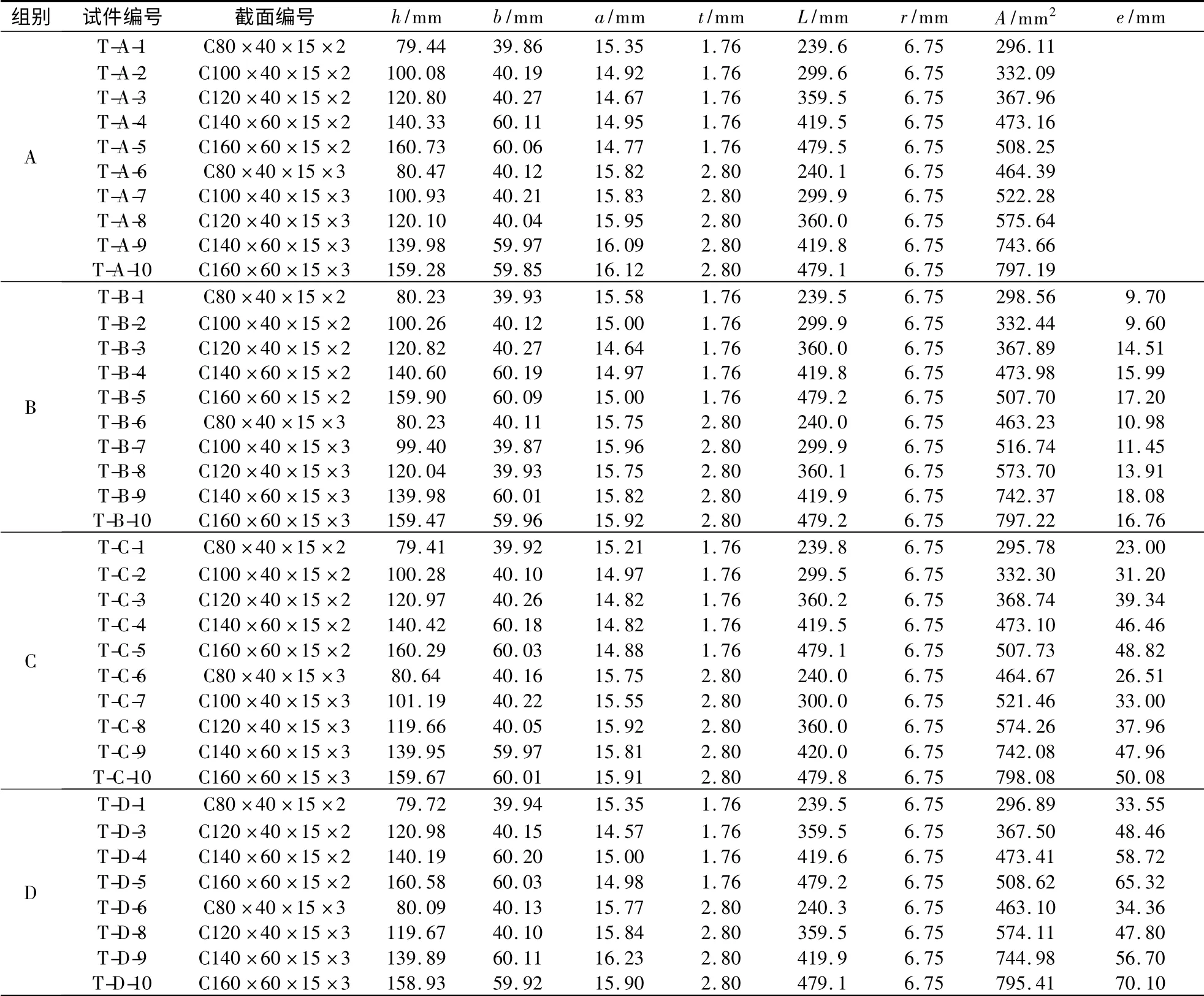
表1 试验试件分组与几何尺寸

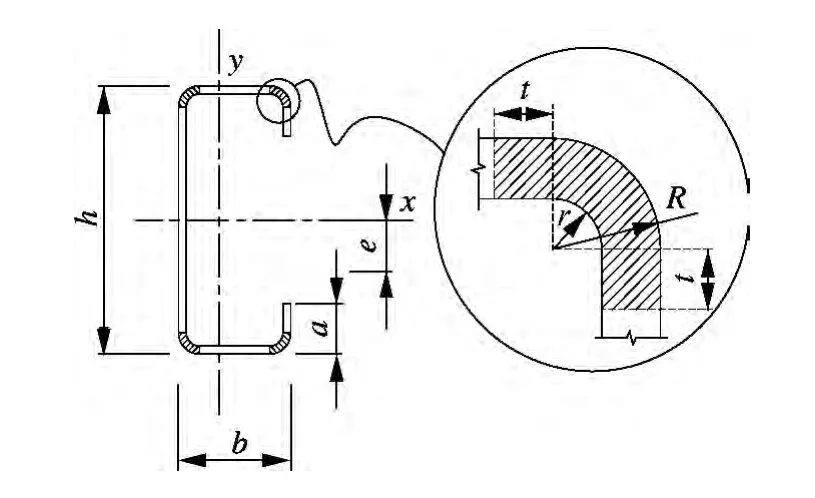
图5 试验试件截面尺寸

表2为卷边C 形截面不锈钢短柱试验试件极限承载力的有限元结果与试验结果对比.由表可知，有限元结果与试验结果的平均误差为－0.77%，且误差大部分在6%以内，说明有限元计算分析模型能够较好地预测不锈钢短柱的极限承载力.

3 承载力计算公式

3.1 轴心受压构件

为了确定式(3)中各待定系数值，对98 根卷边C 形截面轴心受压不锈钢短柱试件开展有限元计算分析，获得各试件的极限承载力值Pnλ.试件的截面类型、截面厚度与试件数量见表3.对于截面型号相同的试件，通过改变试件厚度t 来改变截面柔度系数λ1.根据欧洲规范EN1993-1-4 规定［11］，为了在有限元模拟分析中既能反映构件截面受力特性又不会发生整体失稳，短柱试件长度的取值应限制在3 倍截面最大宽度和20 倍截面最小回转半径之间.本文中将卷边C 形截面不锈钢短柱试件长度按3 倍截面最大宽度来确定.

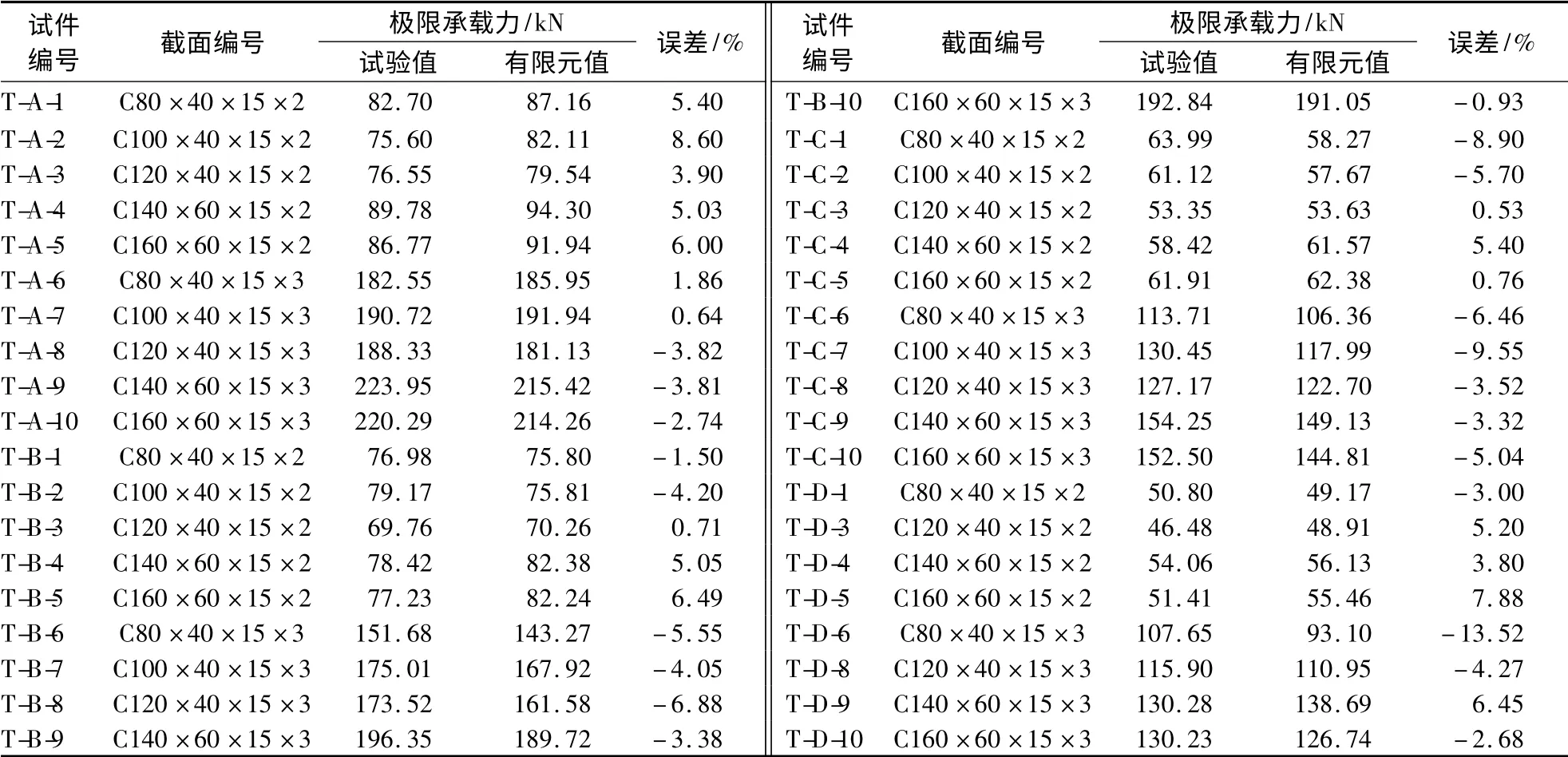
表2 有限元分析结果与试验结果的对比

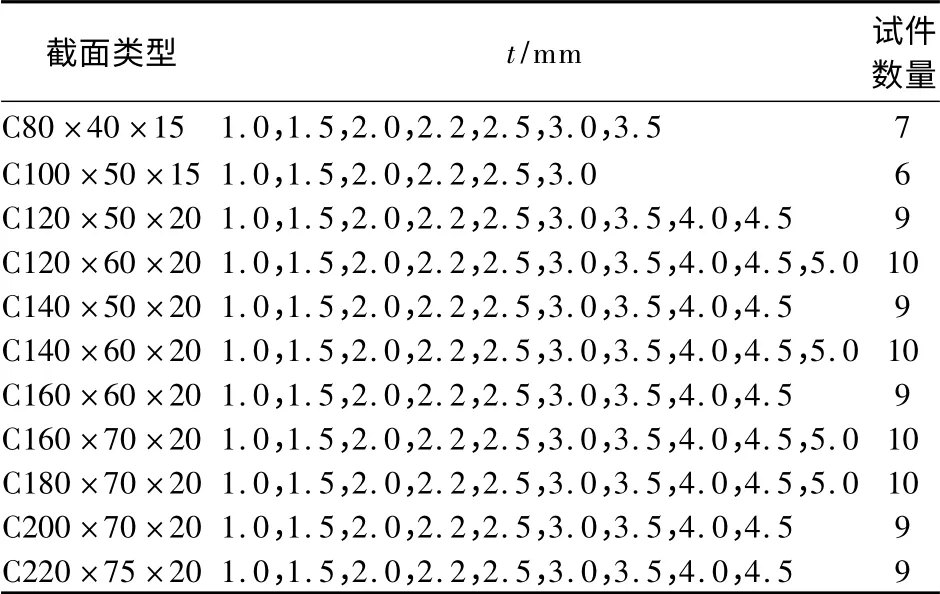
表3 轴心受压不锈钢短柱试件的截面类型、厚度与数量

首先，利用有限条软件CUFSM 计算出98 根短柱试件的临界应力值σcr;然后，确定各试件的截面柔度系数假定短柱试件的全截面有效，计算试件轴压承载力Pne.各试件的临界应力值σcr、截面柔度系数λ1、极限承载力值Pnλ及轴压承载力值Pne参见文献［6］.

根据98 根短柱试件的截面柔度系数λ1与极限承载力值Pnλ，利用Datefit8.0 软件进行数据拟合，可获得式(3)中各待定系数为:a1=0.973，b1=0.209，c=0.45，λlimit1=0.386.适用于轴心受压不锈钢短柱承载力Pnλ的计算公式为

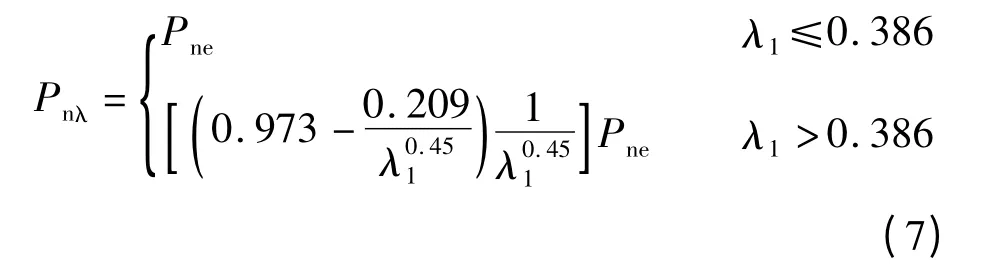
图6(a)为式(7)计算出的98 根短柱试件承载力结果与有限元结果的对比.由图可见，有限元数据点与拟合曲线比较接近，两者误差的平均值为－8.20%，方差为1.16%.由于截面柔度系数较大的构件数据点偏少，故λ1≥3 时拟合公式的预测值可靠性不高.

有限元计算分析模型中未考虑转角区不锈钢材料强度的提高对构件极限承载力的影响，因此按式(7)计算出的轴心受压不锈钢短柱承载力值并不是构件的实际极限承载力，应按下式对承载力值进行修正:

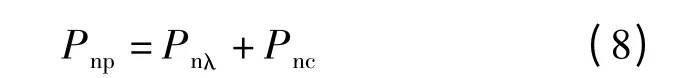
式中，Pnp为考虑转角区的材料强度提高后短柱试件承载力值;Pnλ为按式(7)计算出的短柱试件承载力值;Pnc=(σc0.2－σ0.2)Ac为考虑转角区的材料强度对短柱试件承载力的提高值，其中σc0.2为转角区不锈钢材料的名义屈服强度，可由转角区不锈钢材料力学性能试验结果确定［6-7］，Ac为试件转角区的总面积.

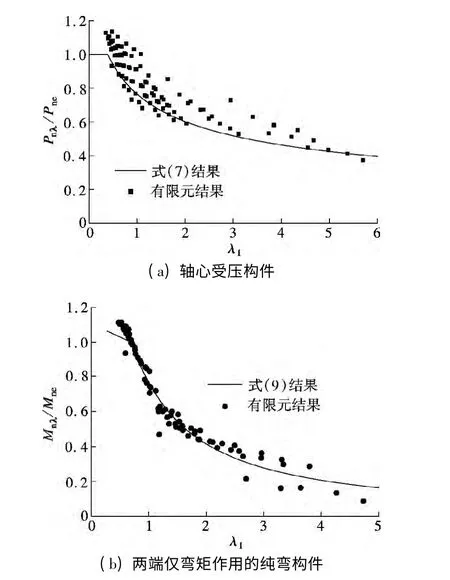
图6 不锈钢短柱试件承载力的拟合结果与有限元结果对比

3.2 两端受弯矩作用的纯弯构件

为了确定式(4)中各待定系数值，对94 根两端受弯矩作用的卷边C 形截面不锈钢纯弯试件开展有限元计算分析，获得各试件的极限弯矩值Mnλ.试件的截面类型、截面厚度与试件数量见表4.对于截面型号相同的试件，通过改变试件厚度t来改变构件截面柔度系数λ1.试件长度的取值同轴心受压不锈钢短柱.

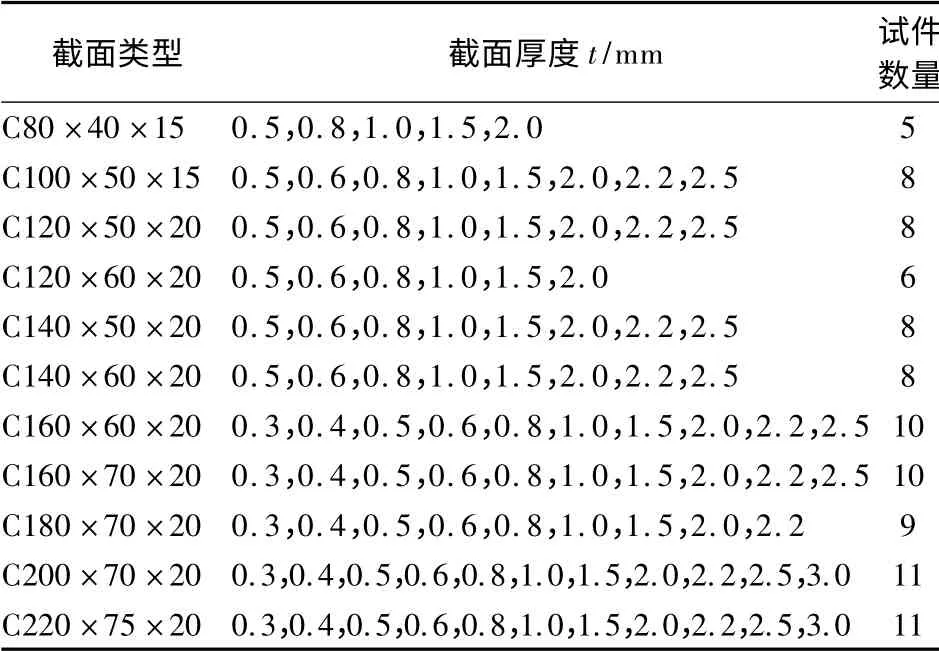
表4 纯弯不锈钢短柱试件的截面类型、厚度与数量

首先，利用有限条软件CUFSM 计算出94 根试件的临界弯矩值Mcr;然后，确定各试件的截面柔度系数假定试件的全截面有效，计算出试件理论弯矩值Mne.各试件的临界弯矩值Mcr、截面柔度系数λ1、极限承弯矩值Mnλ及理论弯矩值Mne参见文献［6］.

根据94 根不锈钢纯弯试件的截面柔度系数λ1与极限弯矩值Mnλ，利用Datefit8.0 软件进行数据拟合，可获得式(4)中的各待定系数为:a2=0.984，b2=0.217，d=1.09，λlimit2=0.673.在拟合过程中，实际上仅采用了78 根试件的数据点，其他数据点被摒弃.主要原因为:对于截面柔度系数λ1较小的试件，试件应力水平较高且超出不锈钢材料模型(式(5))的适用范围，导致试件承载力比值Mnλ/Mne随柔度λ1减小而减小，故删除了截面柔度系数λ1较小的试件数据.卷边C 形截面不锈钢纯弯构件的极限弯矩值Mnλ为

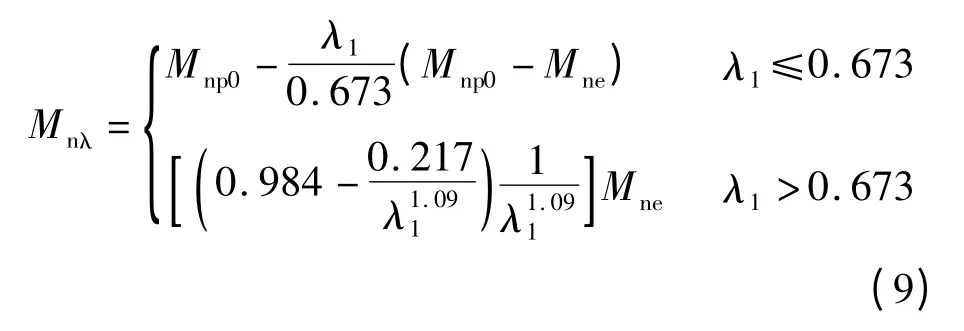
式中，Mnp0为不考虑转角区材料强度提高的纯弯试件塑性弯矩值.

图6(b)为式(9)计算出的78 根试件承载力结果与有限元结果的对比.由图可见，有限元数据点与拟合曲线较为接近，两者误差的平均值为0.8%，方差为5.7%.

计算分析模型中未考虑转角区不锈钢材料强度的提高对构件承载力的影响，因此按式(9)计算出的极限弯矩值并不是构件的实际极限弯矩值，需按下式对极限弯矩值进行修正:

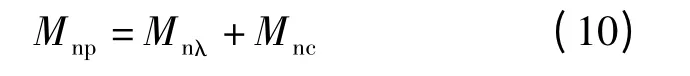
式中，Mnp为考虑转角区的材料强度提高后试件的极限弯矩值;Mnc为考虑转角区的材料强度对试件极限弯矩的提高值.

卷边C 形截面偏心受压不锈钢短柱的承载力可按下式确定:

式中，Pnm为偏心受压不锈钢短柱的承载力;Pnp为轴心受压不锈钢短柱的极限承载力，可由式(8)计算得到;Mnp为不锈钢纯弯构件的极限弯矩值，可由式(10)计算得到.

4 拟合公式与试验结果对比

为了验证拟合公式的正确性，按照式(8)和(11)分别计算出38 根卷边C 形截面不锈钢短柱试验试件的承载力，并将计算结果与试验结果进行对比分析.采用式(8)和(11)计算试验试件承载力时，应遵循以下原则:①试件的截面几何参数均采用实测值(见表1);②不锈钢平板区和转角区的材料性能分别采用平板区标准试件和转角区标准试件试验所获得的材料力学性能.

对于轴心受压不锈钢短柱试验试件，由式(8)计算出的极限承载力与试验结果Ftest对比见表5.由表可知，拟合公式结果与试验结果吻合较好，平均误差为4.51%，表明轴心受压不锈钢短柱极限承载力的拟合公式具有较高的精确性.

对于B，C，D 组偏心受压不锈钢短柱试验试件，由式(11)计算出的极限承载力与试验结果对比见表6.由表可知，拟合公式结果与试验结果吻合较好，表明拟合公式可以较为准确地预测偏心受压不锈钢短柱的极限承载力.

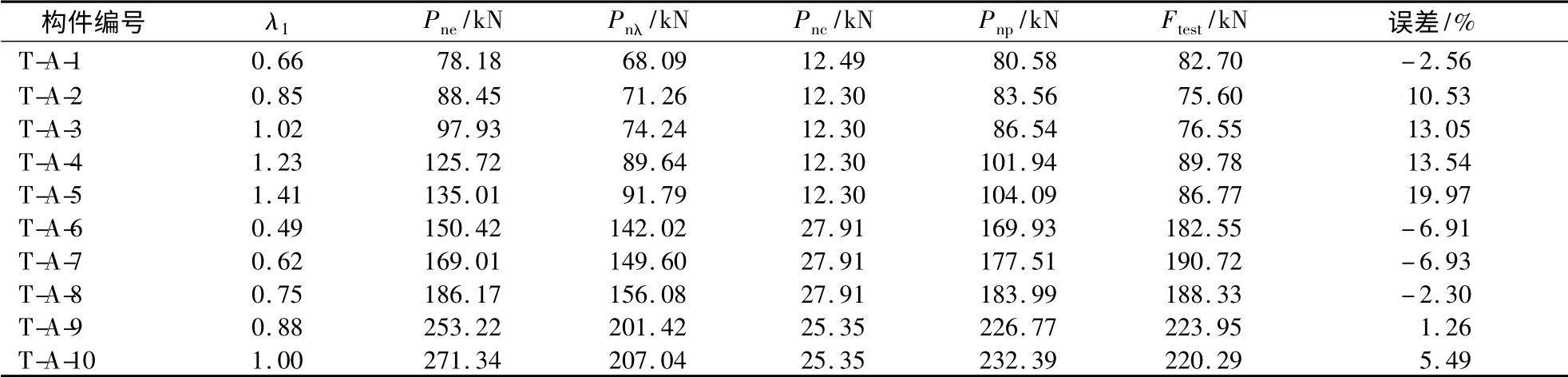
表5 A 组试验试件承载极限力的拟合公式计算结果与试验结果对比

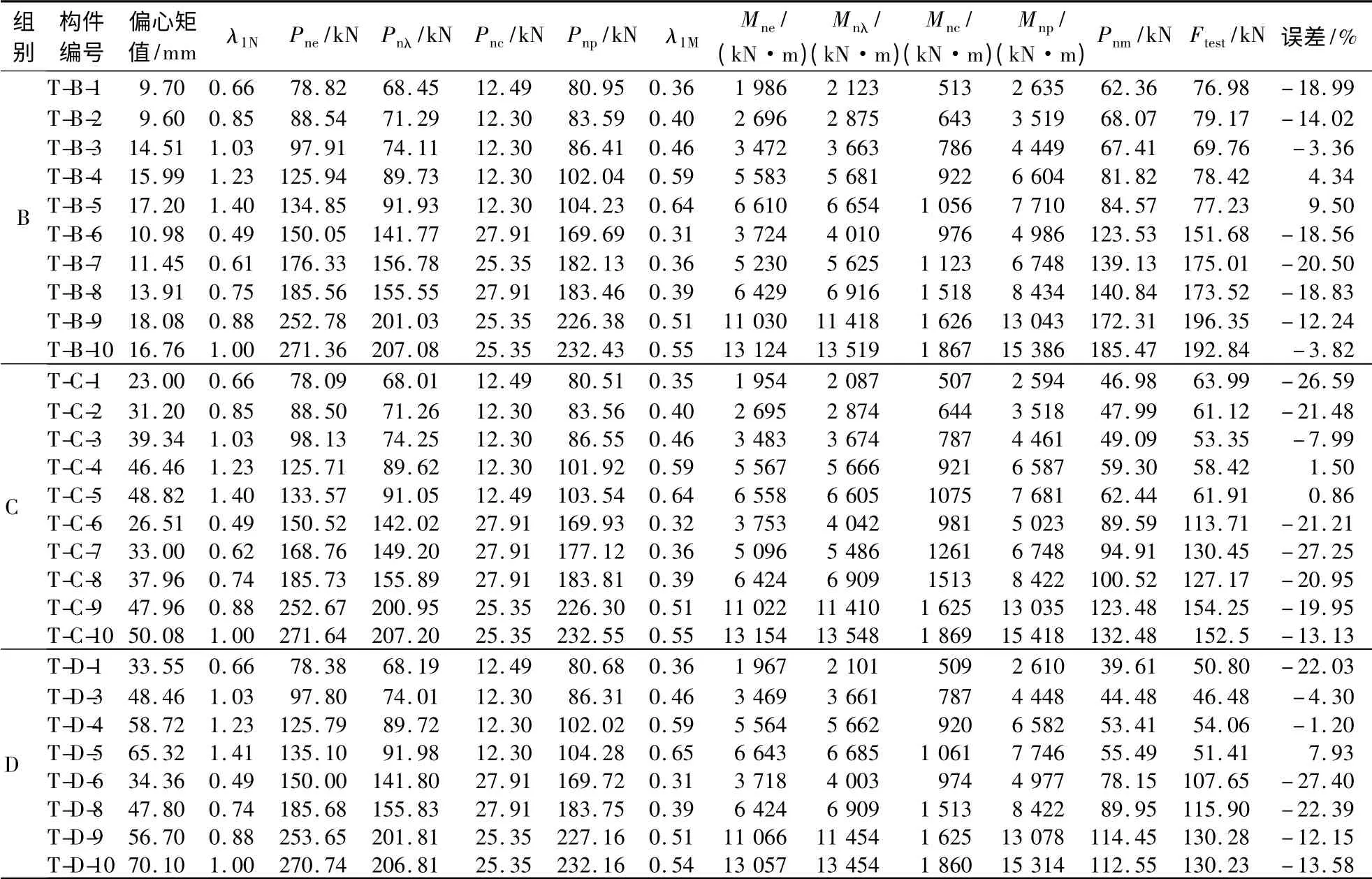
表6 B，C 和D 组试验试件承载极限力的拟合公式计算结果与试验结果对比

5 结论

1)与传统的有效截面计算方法相比，直接强度法以构件全截面为对象，以全截面特性进行承载力计算，计算方法简单，是一种较为准确的新方法，可以方便计算带有复杂加劲截面构件的承载力.

2)基于直接强度法，提出了卷边C 形截面不锈钢短柱在轴心受压和两端受弯矩作用2 种受力状态下的承载力计算假定模型.通过对98 根轴心受压和94 根不锈钢纯弯试件进行有限元数值模拟分析，拟合出适用于卷边C 形截面不锈钢短柱极限承载力的直接强度法计算公式.

3)结合已开展的38 根不锈钢短柱试件试验结果，对拟合公式进行验证.结果表明，本文拟合出的直接强度法计算公式可以较好地预测卷边C 形截面不锈钢短柱承载力.

References)

［1］ Schafer B W.Review:the direct strength method of cold-formed steel member design［J］.Journal of Constructional Steel Research，2008，64(7):766-788.

［2］ Leng J，Guest J K，Schafer B W.Shape optimization of cold-formed steel columns［J］.Thin-Walled Structures，2011，49(12):1492-1503.

［3］ Lecce M，Rasmussen K J R.Distortional buckling of cold-formed stainless steel sections:experimental investigation［J］.Journal of Structural Engineering，2006，132(4):497-504.

［4］ Lecce M，Rasmussen K J R.Distortional buckling of cold-formed stainless steel sections:finite-element modeling and design［J］.Journal of Structural Engineering，2006，132(4):505-514.

［5］ Becque J，Lecce M，Rasmussen K J R.The direct strength method for stainless steel compression members［J］.Journal of Constructional Steel Research，2008，64(11):1231-1238.

［6］ 刘芳.不锈钢C 形截面短柱有效截面计算方法理论与试验研究［D］.南京:东南大学土木工程学院，2012.

［7］ Fan S，Liu F，Zheng B，et al.Experimental study on bearing capacity of stainless steel lipped C section stub columns［J］.Thin-Walled Structures，2014，83:70-84.

［8］ American Iron and Steel Institute.North American specification for the design of cold formed steel structures.Appendix 1:design of cold-formed steel structural members using the direct strength method［S］.Washington DC，USA:American Iron and Steel Institute，2004.

［9］ AS/NZS 4600-2005 Australia/New Zealand standard:cold-formed steel structures ［S］.Sydney，Australia:Australia/New Zealand Standards，2005.

［10］ Gardner L.A new approach to stainless steel structural design［D］.London:Imperial College，2002.

［11］ European Committee for Standardization.EN 1993-1-4.Euro code 3:design of steel structures-part 1-4:general rules-supplementary rules for stainless steels［S］.Brussels，Belgium:European Committee for Standardization，2006.