磁流变液双链密排微结构模型

许飞鸿 徐赵东 陈兵兵

(东南大学混凝土及预应力混凝土结构教育部重点实验室，南京210096)

磁流变液(MRF)是一种智能材料［1］，是由铁磁颗粒、载体液和添加剂组成.在磁场作用下，能在毫秒级实现黏性流态到类固态的转化，并且具有可逆性.基于MRF 研制的磁流变阻尼器(MRD)已广泛应用于土木、车辆、航空航天等领域的振动控制中［2-3］.在进行振动控制分析时，首先要计算MRF 的剪切屈服应力，很多学者都对此进行了研究.

宏观现象模型［1，4-5］形式简洁，应用方便，但不能反映剪切屈服应力与各影响因素的关系，因此很多学者从微观结构层面对磁流变液的剪切屈服应力进行了研究.李海涛等［6］基于磁偶极子理论深入研究了磁流变液的成链机理.Ginder 等［7］利用非线性有限元方法计算了单链中颗粒间的作用力，考虑了磁饱和效应的影响，但是该模型不能反映铁磁颗粒体积分数的影响.Peng 等［8-9］基于磁偶极子理论，采用统计学方法假定链达到动态平衡后与磁场方向的夹角符合正态分布，得到了磁流变液的剪切屈服应力，并且深入分析了各因素对剪切屈服应力的影响.但是以上文献均与所假设的链相距很远，从而忽略相邻链之间的相互作用，与实际情况不符.文献［10］表明随着铁磁颗粒体积分数以及磁场的增大，相邻2 条链会错位排列积聚在一起，形成比单链更加稳定的双链密排结构.鉴于此，本文基于磁偶极子理论，根据磁流变液的链化机理，并考虑相邻链之间的相互作用，提出了更为精确的磁流变液双链密排微结构模型，并采用统计学方法从能量角度对磁流变液的剪切屈服应力进行了推导，分析了各主要因素对磁流变液剪切屈服应力的影响规律，并根据文献［10-12］中的试验结果对模型进行了验证.

1 理论分析

在外加磁场下，磁流变液中的铁磁颗粒被磁化，形成沿磁场方向排列的链状结构.随着铁磁颗粒体积分数以及磁场的不断增大，相邻2 条单链会错位排列积聚在一起，形成双链密排结构［10］.这种结构比单链结构的能量小，更加稳定，易于形成，如图1所示.被磁化的颗粒可以看作磁偶极子，基于磁偶极子理论，可以得到单位长度的一个双链密排结构中磁偶极子所具有的总磁能，进而对应变求导得到一个双链密排结构所能提供的剪切屈服应力.由于在剪切作用下，链在偏转过程中会发生断裂和重组，在达到动态平衡时，不同的密排结构与磁场方向的夹角不尽相同，引入统计学的方法，便可得到磁流变液的剪切屈服应力.

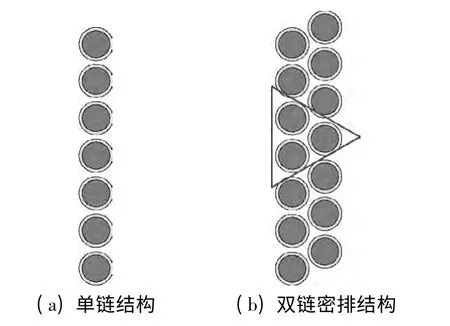
图1 磁偶极子的链化结构

根据上述假设，任取图1中双链密排结构的一个微元进行分析，其受剪变形如图2所示.当2 条链形成双链密排结构时，假定每个颗粒之间的距离相等为d0，α=π/3.在剪切作用下，若j 粒子发生剪切位移x，则k 粒子的位移x0=x/2.θ 为j 粒子发生位移对应的转角，β 为k 粒子发生位移对应的转角，在小变形的情况下，β=θ/2.

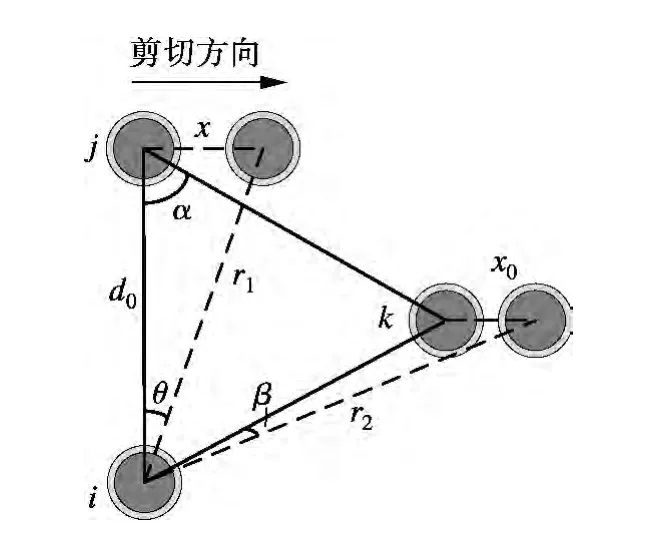
图2 磁偶极子链剪切变形图

根据磁偶极子理论，任意磁偶极子j 在i 处产生的磁能可表示为［12］

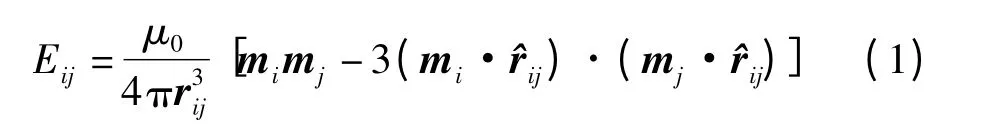
式中，真空磁化率μ0=4π×10－7;rij为两磁偶极子之间的距离矢量;mi为第i 个磁偶极子的偶极距.

对于磁偶极子i，其磁矩mi可按下式计算［12］:

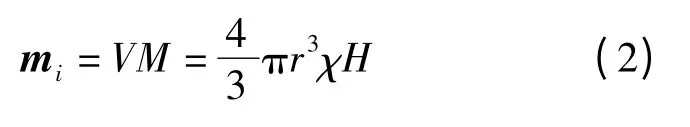
式中，r 为球形铁磁颗粒的半径;H 为磁场强度;χ为铁磁颗粒的磁化率;V 为球形铁磁颗粒的体积;M 为磁矩.

由式(1)可知，磁偶极子间的相互作用能与距离呈三次方关系，即次相邻颗粒在基准颗粒处产生的磁能是相邻颗粒在基准粒子处产生磁能的0.125倍，故起主要作用的是相邻的磁偶极子.因此在计算磁偶极子i 所具有的磁能时，考虑链内其他所有磁偶极子在i 处产生的磁能Ei1;相邻链由于影响稍弱，在此仅考虑i 附近上下2 个磁偶极子的相互作用能Ei2.由于颗粒直径很小，这里假设链为无限长，由式(1)可计算得到磁偶极子i 所在链的其他颗粒在i 处产生的磁能为

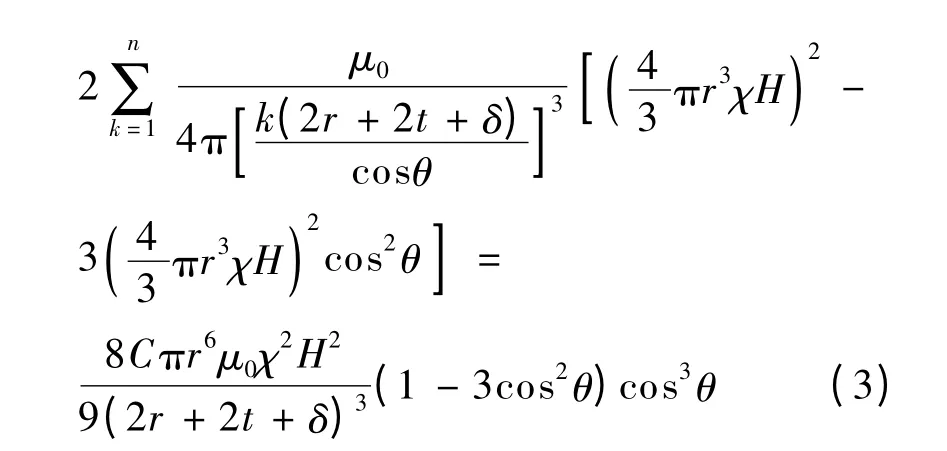
式中，t 为铁磁颗粒外的包覆层厚度;δ 为2 个颗粒间的净距离;

相邻链中磁偶极子i 上下2 个颗粒在i 处产生的磁能为

因此磁偶极子i 所具有的总磁能为

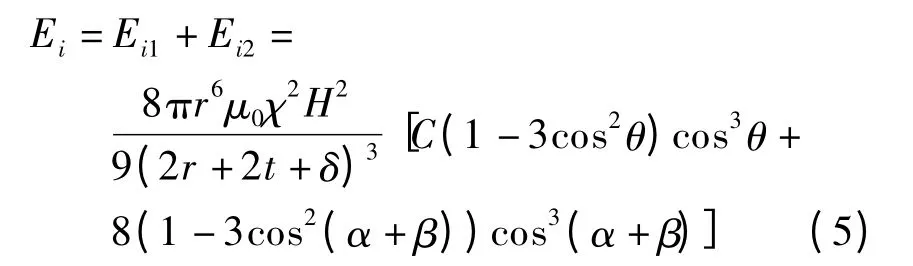
设一个双链密排结构中的磁偶极子数为n，则一个双链密排结构单位长度所具有的磁能为

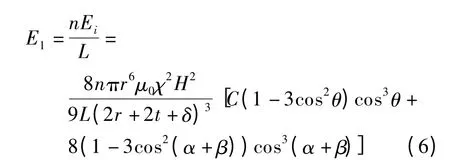
式中，L 为双链密排结构的长度.对式(6)应变进行求导，即可得到一个双链密排结构所提供的剪切屈服应力，即

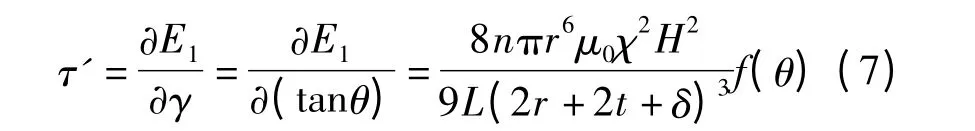
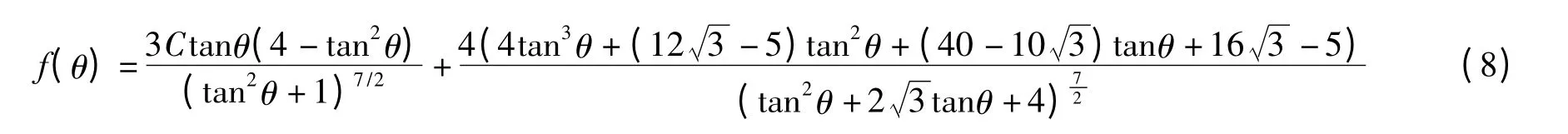
磁流变液的剪切屈服应力即为单位面积内所有的双链密排结构所提供的剪切屈服应力之和，即

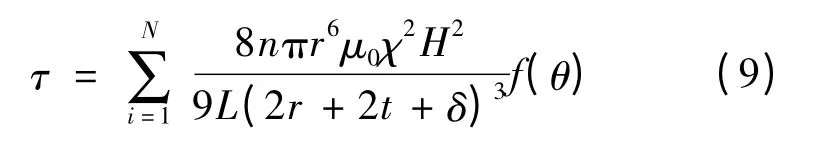
在剪切过程中，链会发生断裂和重组，最终达到动态平衡，此时所有的双链密排结构与磁场方向的夹角不尽相同.这里引入统计学的方法，假设所有链与磁场方向的夹角在区间服从指数分布，通过积分求和便可得到磁流变液的剪切屈服应力，即

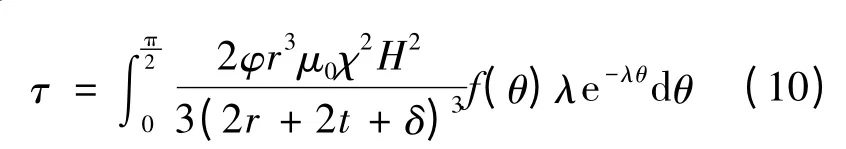
通常容易测量的数据是磁流变液的磁感应强度，而不是磁场强度，因此将式(10)中的磁场强度用磁流变液磁感应强度替换.磁场强度与磁感应强度的关系可按下式表示:

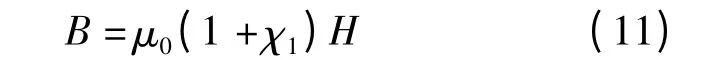
式中，χ1为磁流变液的磁化率.由于颗粒的磁化是非线性的，而且非常复杂，本文采用Frohlish-Kennelly 方程［8］来计算磁化率.

对于铁磁颗粒，有μ0Md=2.1，因此有

对于磁流变液，有μ0Ms=2.1φ，因此有

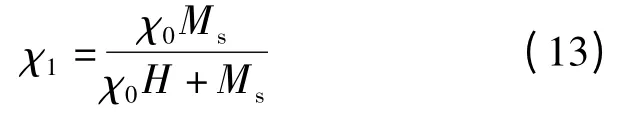
式中，Md和Ms分别为铁磁颗粒和磁流变液的饱和磁化强度.初始磁化率χ0=1 000，将式(11)代入式(10)，可得到磁流变液的剪切屈服应力为

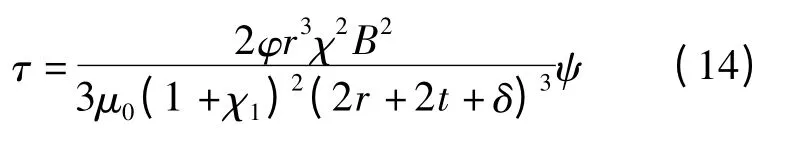
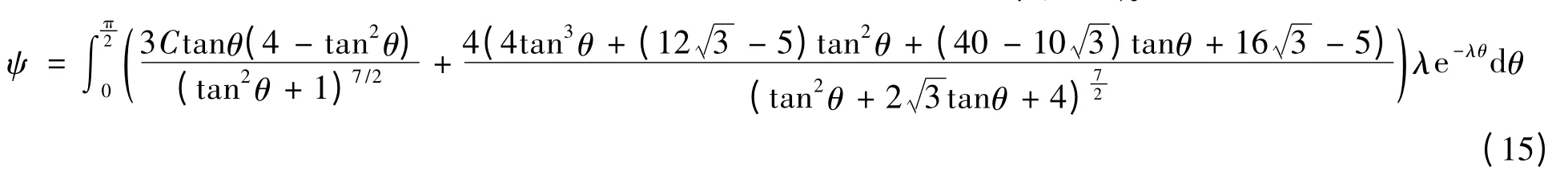
式(14)即为本文所提出磁流变液双链密排结构的剪切屈服应力公式.

2 计算结果分析

针对上述对磁流变液剪切屈服应力的理论分析，下面给出了本文所提出模型的计算结果，并分析了各主要因素对磁流变液剪切屈服应力的影响.

2.1 磁感应强度的影响

图3为磁流变液剪切屈服应力随磁流变液磁感应强度的变化曲线，相关参数为r=5 μm，t=0.5 μm，δ=0.5 μm，ψ=3.98，φ=0.32.由图3(a)可知，屈服应力呈S 形增长，最终达到磁饱和.图3(b)将本文所提出模型的计算结果与文献［11］中的试验结果进行了对比，由图可见，二者吻合很好.

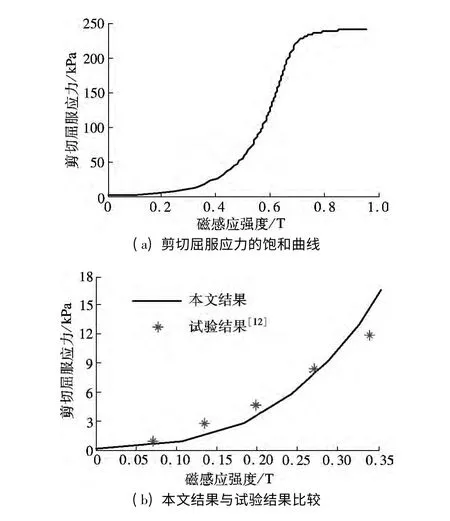
图3 剪切屈服应力与磁感应强度的关系曲线

2.2 铁磁颗粒体积分数的影响

图4(a)为不同磁感应强度下剪切屈服应力与铁磁颗粒体积分数的关系，并与文献［10］中的试验结果进行了对比，二者吻合很好，其中参数ψ 分别为20.12 和0.87，其余参数取值同上.由图可知，随着铁磁颗粒体积分数的增加，剪切屈服应力呈线性增加趋势，这是因为磁流变液的剪切屈服应力主要是由铁磁颗粒磁化后的相互作用决定的.但是在配制磁流变液时，铁磁颗粒体积分数也不能太大，因为体积分数越大，其零场黏度越大，从而导致可调性变差，因此在配制磁流变液时应确定合理的铁磁颗粒体积分数.

2.3 铁磁颗粒尺寸的影响

图4(b)为磁流变液剪切屈服应力随铁磁颗粒尺寸的变化曲线，参数取值为B=0.613 T，ψ=1.28.从图4(b)中可以看出，磁流变液剪切屈服应力随着铁磁颗粒半径的增大而增大，最终趋于平缓，但是随着颗粒尺寸的增大，颗粒的沉降性增强，又会降低磁致效应.因此，应开展对沉降性与颗粒尺寸关系的研究，综合比较以确定铁磁颗粒的最优尺寸.

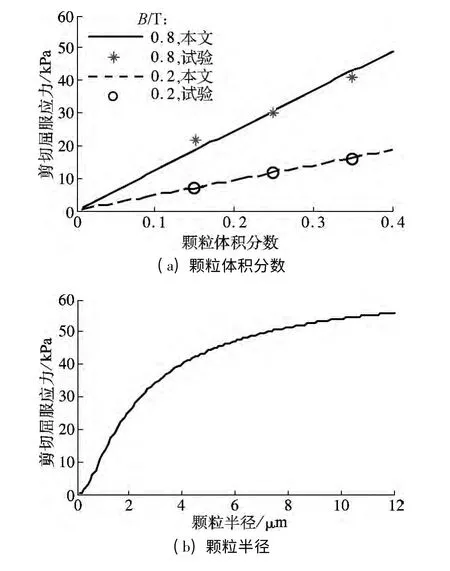
图4 剪切屈服应力与铁磁颗粒的关系曲线

2.4 包覆层厚度的影响

图5为磁流变液剪切屈服应力与铁磁颗粒包覆层厚度的关系曲线，参数取值同上.从图5中可以看出，随着包覆层厚度的增大，剪切屈服应力不断减小，然后趋于平缓.这是因为随着包覆层厚度的增加，颗粒间距变大，导致屈服应力降低.但增大包覆层厚度，可以改善其抗沉降性.因此实际配制磁流变液时应确定合理的包覆层厚度.

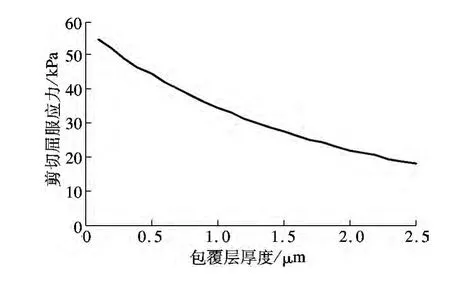
图5 剪切屈服应力与包覆层厚度的关系曲线

3 结语

本文基于磁偶极子理论，结合铁磁颗粒的链化机理，提出了磁流变液双链密排微结构模型，并采用统计学的方法从能量角度推导了磁流变液的剪切屈服应力公式.计算结果表明:磁流变液剪切屈服应力随着磁感应强度的增加而增加，达到磁饱和后基本保持不变;剪切屈服应力随着铁磁颗粒体积分数的增加而线性增加;剪切屈服应力随着颗粒尺寸的增加而增加，随着包覆层厚度的增加而减小，变化幅度最终都趋于平缓.所提出的模型与试验结果吻合很好，而且可以综合反映各主要影响因素与磁流变液剪切屈服应力的关系，可以为高性能磁流变液的研制和优化提供指导.

References)

［1］ Jolly M R，Bender J W，Carlson J D.Properties and applications of commercial magnetorheological fluids［J］.Journal of Intelligent Material Systems and Structures，1999，10(1):5-13.

［2］ Dyke S J，Spencer Jr B F，Sain M K，et al.An experimental study of MR dampers for seismic protection［J］.Smart Materials and Structures，1998，7(5):693-703.

［3］ Xu Zhaodong，Sha Lingfeng，Zhang Xiangcheng，et al.Design，performance test and analysis on magnetorheological damper for earthquake mitigation［J］.Structural Control and Health Monitoring，2013，20(6):956-970.

［4］ Bitman L，Choi Y T，Wereley N M.Electrorheological damper analysis using an Eyring constitutive relationship［J］.Journal of Intelligent Material Systems and Structures，2002，13(10):633-639.

［5］ 翁建生，胡海岩，张庙康.磁流变液体的流变力学特性试验和建模［J］.应用力学学报，2000，17(3):1-5.Weng Jiansheng，Hu Haiyan，Zhang Miaokang.Experimental and modeling study on rheological properties of a kind of magnetorheological fluid［J］.Chinese Journal of Applied Mechanics，2000，17(3):1-5.(in Chinese)

［6］ 李海涛，彭向和，陈伟民.基于链化分析的磁流变液剪切屈服应力模型［J］.化学物理学报，2005，18(4):505-509.Li Haitao，Peng Xianghe，Chen Weimin.Yield shearstress model of magnetorheological fluids［J］.Chinese Journal of Chemical Physics，2005，18(4):505-509.(in Chinese)

［7］ Ginder J M，Davis L C.Shear stresses in magnetorheological fluids:role of magnetic saturation［J］.Applied Physics Letters，1994，65(26):3410-3412.

［8］ Peng X，Li H.Analysis of the magnetomechanical behavior of MRFs based on micromechanics incorporating a statistical approach［J］.Smart Materials and Structures，2007，16(6):2477-2485.

［9］ Yi C，Peng X，Zhao C.A magnetic-dipoles-based micro-macro constitutive model for MRFs subjected to shear deformation［J］.Rheologica Acta，2010，49(8):815-825.

［10］ 易成建.磁流变液:制备、性能测试与本构模型［D］.重庆:重庆大学资源及环境科学学院，2011.

［11］ Li W H，Du H.Design and experimental evaluation of a magnetorheological brake［J］.The International Journal of Advanced Manufacturing Technology，2003，21(7):508-515.

［12］ 池长青，王之珊，赵丕智.铁磁流体力学［M］.北京:北京航空航天大学出版社，1993.