一种改进的永磁直线电机气隙磁场解析计算方法

陈中显 余海涛 胡敏强

(东南大学电气工程学院，南京210096)

永磁直线电机的初级铁芯矩形开槽后，会影响到气隙磁场的分布，一方面气隙磁场产生较多的谐波分量，从而影响到永磁直线电机运行过程中的电动势波形;另一方面气隙磁通的漏磁系数增大，降低了永磁体的有效利用率.因此，国内外对永磁直线电机的气隙磁场分布进行了相关的研究.

文献［1-6］采用有限元法分析电机气隙磁场的分布情况，但有限元法计算耗时较长，因而不适用于永磁直线电机的初步设计和优化.文献［7-11］采用传统的许-克变换法，对电机的气隙磁场分布进行了解析计算，由于传统的许-克变换法没有充分考虑电机气隙宽度和永磁体厚度对气隙磁场分布的影响，使得解析计算结果与有限元计算结果存在较大的偏差.文献［12］采用分离变量法对永磁直线电机的气隙磁场进行解析计算，但此方法未能合理地求解偏微分方程，致使其解析计算的结果与有限元计算结果存在较大的偏差.

本文分别考虑矩形开槽永磁直线电机的气隙宽度和永磁体厚度因素，对传统的许-克变换坐标系统进行改进，从而建立了一个较为合理的气隙磁场模型.通过该模型，首先推导出永磁直线电机气隙宽度大于或等于初级铁芯齿宽情况下的气隙相对磁导分布函数，然后推导出气隙宽度小于初级铁芯齿宽情况的气隙相对磁导分布函数，并对气隙相对磁导分布函数作了修正.理论推导和真实的数据计算表明，改进的许-克变换解析计算结果更加接近于有限元软件的计算结果.最后，根据改进的许-克变换解析计算方法，对矩形开槽永磁直线电机的气隙磁场分布实施优化设计，试制了一台短次级圆筒型永磁直线发电机，并进行了相关的实验测试.

1 永磁直线电机的气隙磁场模型

永磁直线电机的结构主要由初级铁芯、次级铁芯、绕组、永磁体等部分组成.按照初级铁芯和次级铁芯的长短，可以把永磁直线电机分为短初级和短次级2 种类型.其中，短次级矩形开槽永磁直线电机的基本结构如图1所示.图中，τ 为极距;τp为永磁体长度;ws为槽宽;wt为齿宽;hm为永磁体厚度;h 为合成气隙宽度.

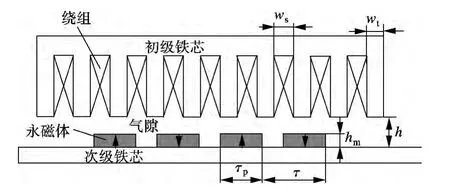
图1 短次级矩形开槽永磁直线电机的基本结构

1.1 初级铁芯无槽情况下的气隙磁场模型

永磁直线电机初级铁芯无槽情况下的气隙磁场模型如图2所示.图中，g 为气隙宽度.通常情况下，为了得到初级铁芯无槽情况下的气隙磁通密度，作如下基本的假设:

①磁场的方向指向±y，且永磁体被均匀磁化;

②把初级铁芯气隙侧表面视作光滑的平面;

③初级铁芯和次级铁芯的磁导率为无穷大，即μx=μy=∞;

④相邻永磁体之间的部分由未被磁化的永磁体充满.

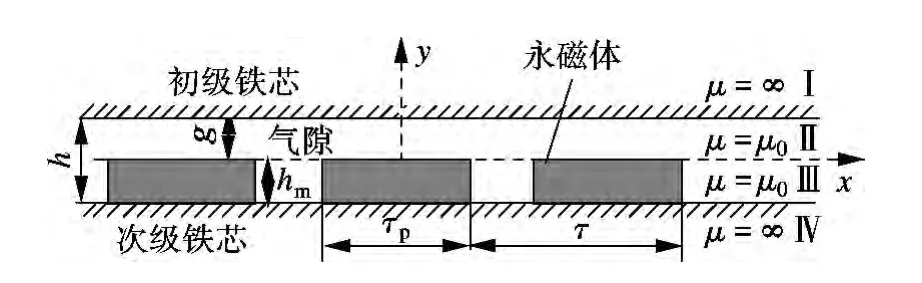
图2 永磁直线电机初级铁芯无槽的气隙磁场模型

根据上述假设，采用等效电流法，得到如下图2的区域磁矢位方程:

1)区域Ⅱ

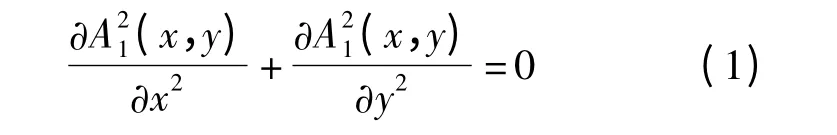
2)区域Ⅲ

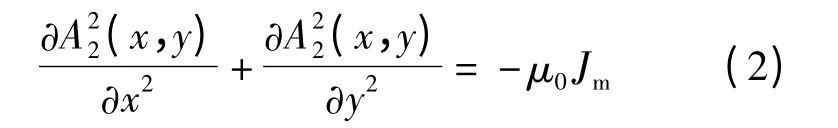
与式(1)和(2)相对应的区域和边界条件如下:

1)区域Ⅱ

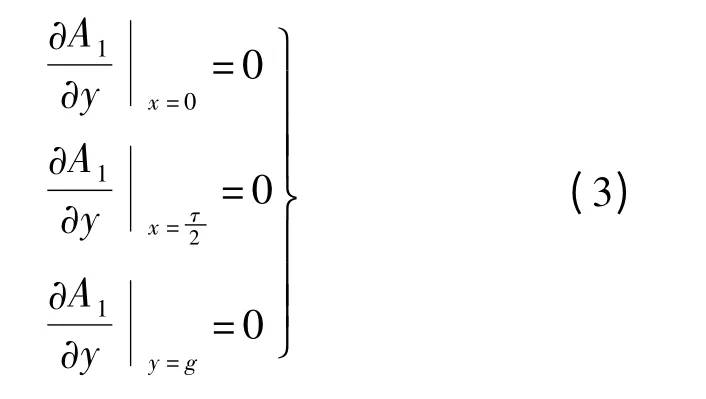
2)区域Ⅲ

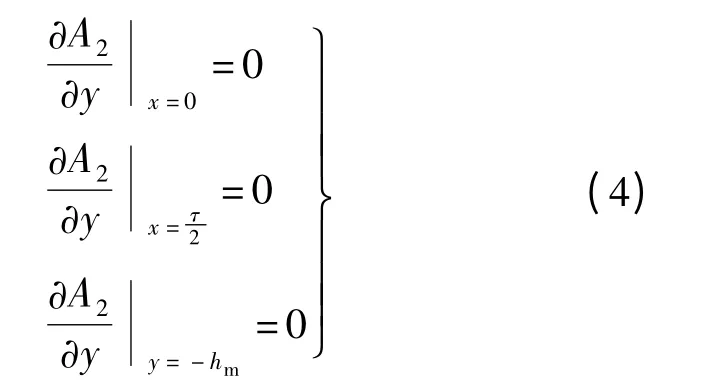
3)区域Ⅱ和Ⅲ交界处

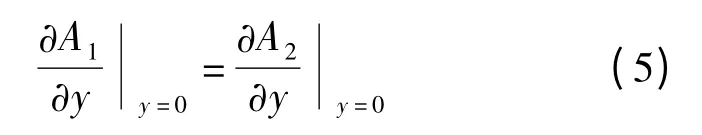
式中，A1和A2为磁矢位;μ0为真空磁导率;Jm为永磁体的等效磁化电流密度［13］，其傅里叶级数形式为

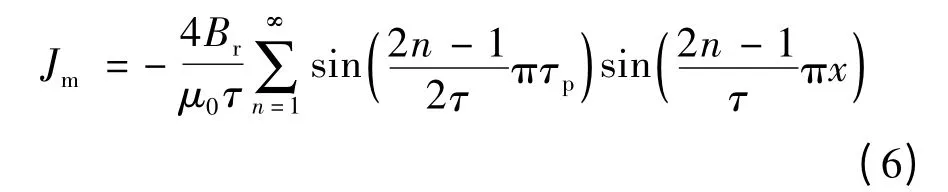
式中，Br为永磁体的剩磁.通过引入区域和边界条件式(3)～(5)，可以得到磁矢位方程(1)和(2)的解，进而可以得到气隙磁通密度分布Bg为

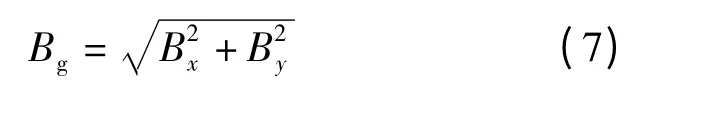
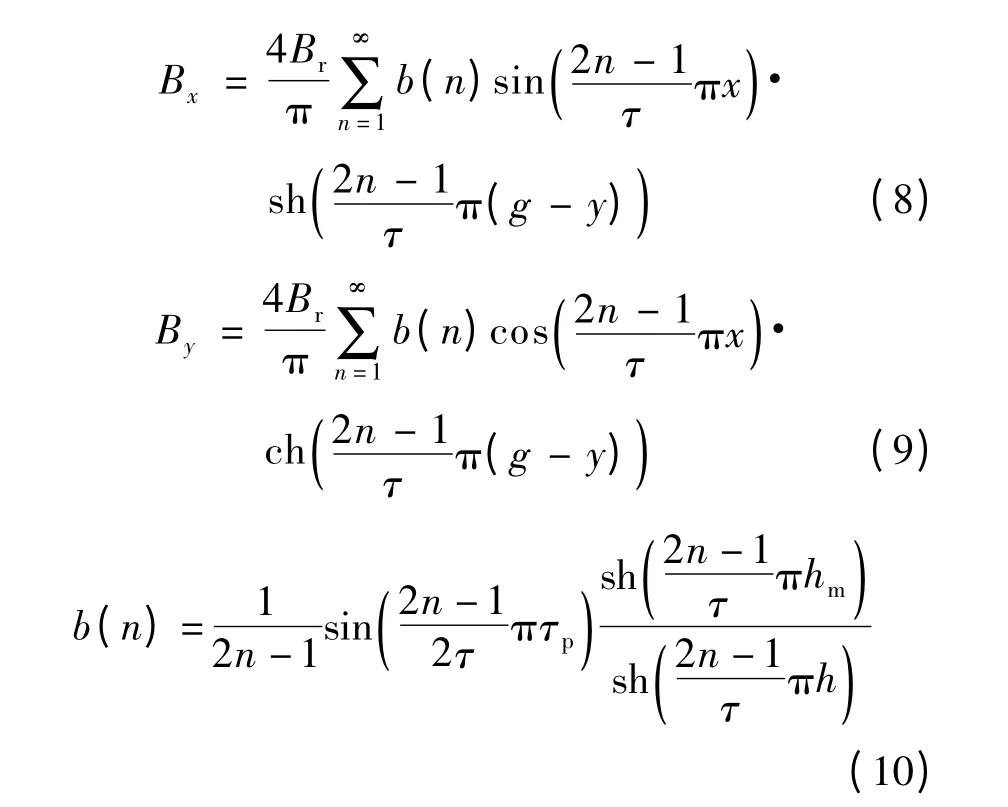
式中，Bx，By分别为x，y 方向的磁通密度.

1.2 初级铁芯矩形开槽的气隙磁场模型

在永磁直线电机初级铁芯矩形开槽情况下，受齿槽效应的影响，气隙磁通密度的谐波分量会增加，从而影响到永磁直线电机运行时的工作质量.本文提出改进的许-克变换解析计算方法，能够分别考虑永磁体厚度和气隙宽度对于气隙磁场分布的影响，且可以通过解析计算得到较为准确的气隙磁场分布，为进一步的永磁直线电机尺寸设计和优化提供参考依据.

改进的许-克变换解析计算方法的变换过程如图3所示，分别考虑永磁直线电机的永磁体厚度和气隙宽度因素，对传统的许-克变换坐标系统进行调整.图3(a)的z 平面坐标系统(x'，y)是在传统的许-克变换坐标系统(x，y)的基础上建立起来的.把图3(a)的z 平面坐标系统(x'，y)变换成图3(b)的w 平面坐标系统(u'，v)，那么，w 平面坐标系统(u'，v)的点u2，u3，u4，u5分别与z 平面坐标系统(x'，y)的点z2，z3，z4，z5一一对应，由许-克变换理论［14-15］可得z 平面变换到w 平面的微商为

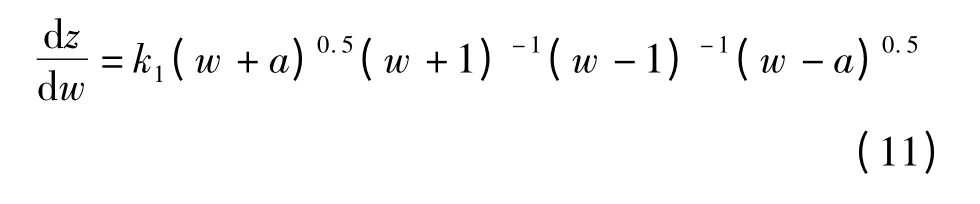
式中，k1=为任意大于1 的常数.对式(11)进行积分可得

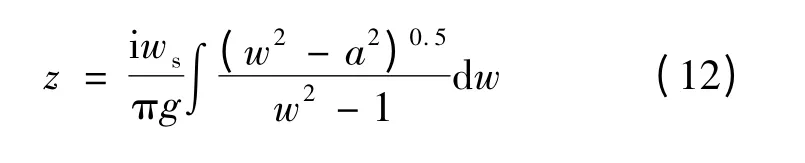
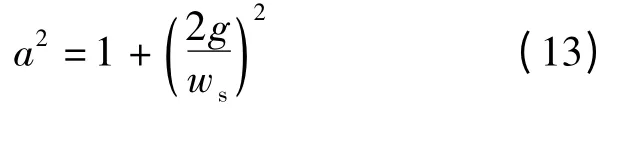
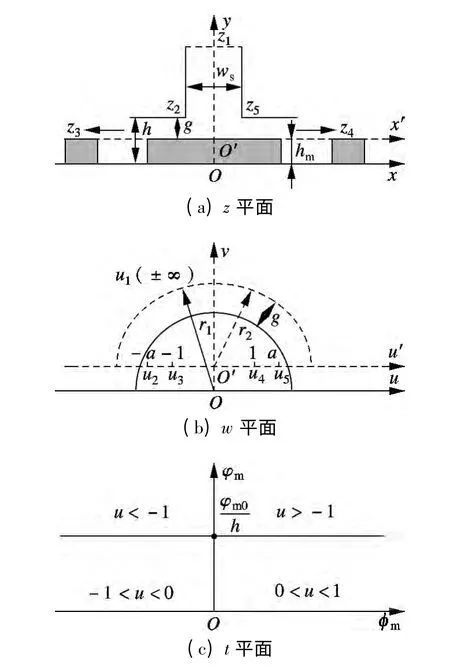
图3 改进的许-克变换过程

为得到永磁直线电机的气隙磁场分布，还需对图3(a)的z 平面进行二次变换，如图3(c)的t 平面所示，其纵坐标φm=0 代表永磁体表面的磁位为零，横坐标代表磁通φm.t 平面的横坐标轴与w平面的横坐标u3u4对应，φm=φm0/h 代表永磁直线电机初级铁芯内表面和槽壁的磁位.根据w 平面的u3= －1 和u4=1，将t 平面对w 平面求导，得

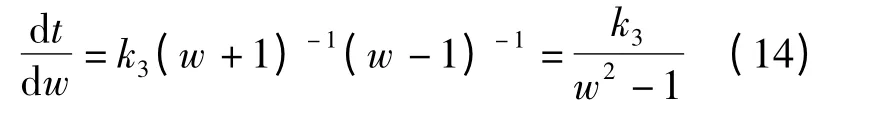
式中，k3=

综上所述，永磁直线电机的气隙磁通密度可以表示为

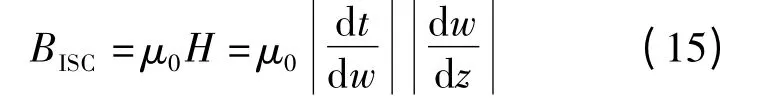
将式(11)和(14)代入式(15)，得

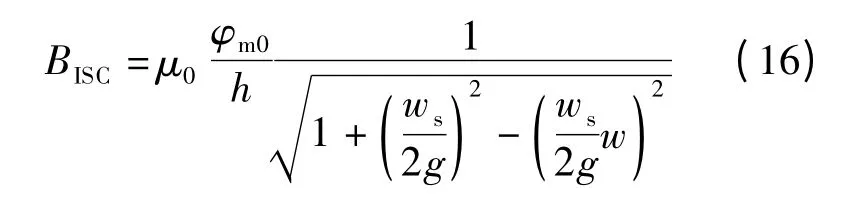
由式(16)可知，与传统的许-克变换法［］相比，改进的许-克变换法获得的气隙磁通密度BISC不仅考虑了永磁直线电机的合成气隙宽度h=hm+g，还考虑了永磁直线电机的气隙宽度g.根据改进的许-克变换法.计算一个槽距内的气隙磁通密度分布过程是:①由式(16)计算出不同w 值(0 ～1)的BISC值;②由式(12)和(13)计算出不同w 值对应的z 值(z=x);③绘制出矩形开槽永磁直线电机一个槽距内的气隙磁通密度分布(即x 与BISC的对应关系).

1.3 气隙相对磁导分布函数

若要更为准确地解析计算一个槽距内的气隙磁通密度分布，还需考虑气隙相对磁导分布函数.根据式(16)和改进的许-克变换过程，令w=u，那么在永磁直线电机的齿中心线上(u=1)，其气隙磁通密度达到最大值，即

在永磁直线电机的槽中心线上(u=0)，其气隙磁通密度达到最小值，即

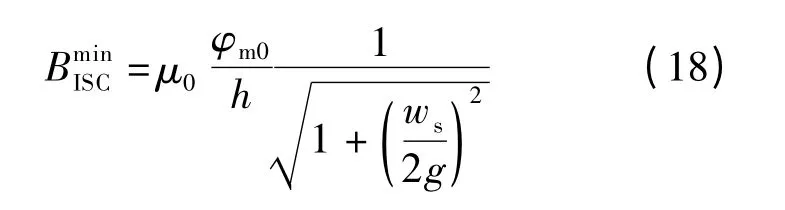
根据式(17)和(18)，可得矩形开槽永磁直线电机的气隙宽度大于等于初级铁芯齿宽(g≥wt)，以及气隙宽度小于初级铁芯齿宽(g ＜wt)情况下的气隙相对磁导分布函数［16］.

综上所述，矩形开槽永磁直线电机的气隙磁通密度B 为

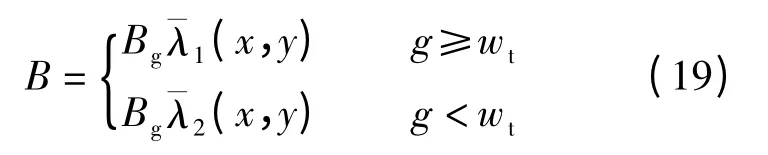
1.4 气隙相对磁导分布函数修正

通过有限元方法进行验证表明，式(19)只能准确地计算与永磁体对应的气隙磁通密度分布，而无法准确地计算永磁体之间(τ －τp)的气隙磁通密度分布，这主要是由于永磁体的边端效应所造成的.

因此，需要对永磁体之间(τ －τp)的气隙相对磁导分布函数予以修正.在选取不同永磁直线电机结构参数的基础上，通过其有限元计算值和改进许-克变换解析计算值的比较，得到二者在永磁体之间(τ－τp)的修正系数为

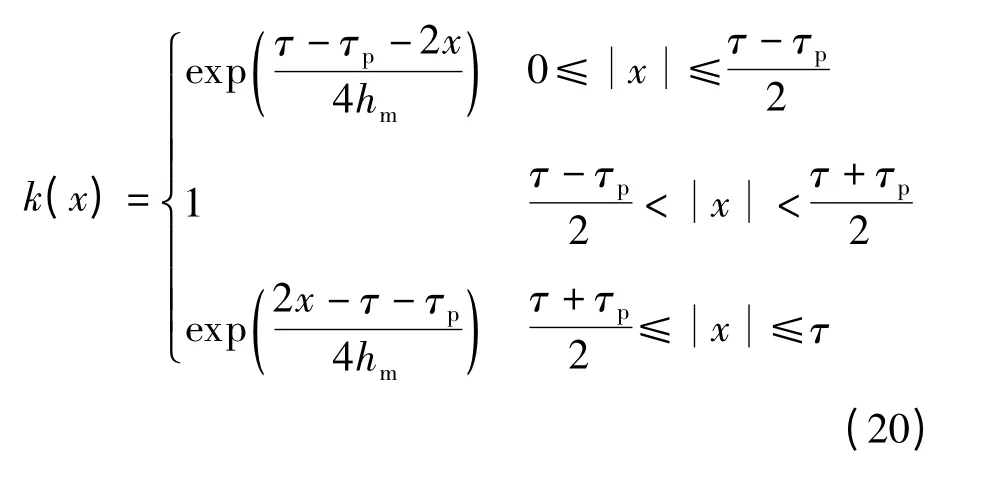
所以，引入修正系数后，矩形开槽永磁直线电机的气隙磁通密度为

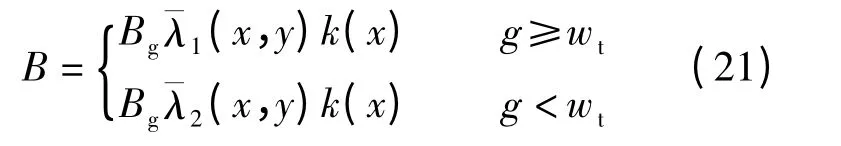
2 气隙磁场解析计算与有限元验证

为了验证本文提出的方法能准确地计算矩形开槽永磁直线电机气隙磁场分布，分别采用改进的许-克变换方法、传统的许-克变换方法和有限元计算方法，对一台矩形开槽圆筒型永磁直线电机的气隙磁场进行计算.该台样机的极距为69 mm，槽宽为7 mm，齿宽为5 mm，永磁体长度为50 mm，永磁体厚度为10 mm，永磁体材料为Nd-Fe-B，矫顽力Hc= －880 kA/m，剩磁Br=1.16 T.

2.1 气隙宽度大于等于初级铁芯齿宽

在矩形开槽永磁直线电机的气隙宽度大于等于初级铁芯齿宽的情况下，通过引入气隙相对磁导分布函数(x，y)和永磁体之间(τ－τp)的修正系数k(x)，其气隙磁通密度的解析计算和有限元计算结果如图4所示.通过图4的有限元验证表明，与传统的许-克变换方法相比，改进的许-克变换方法能够更加准确地计算气隙磁场的分布.

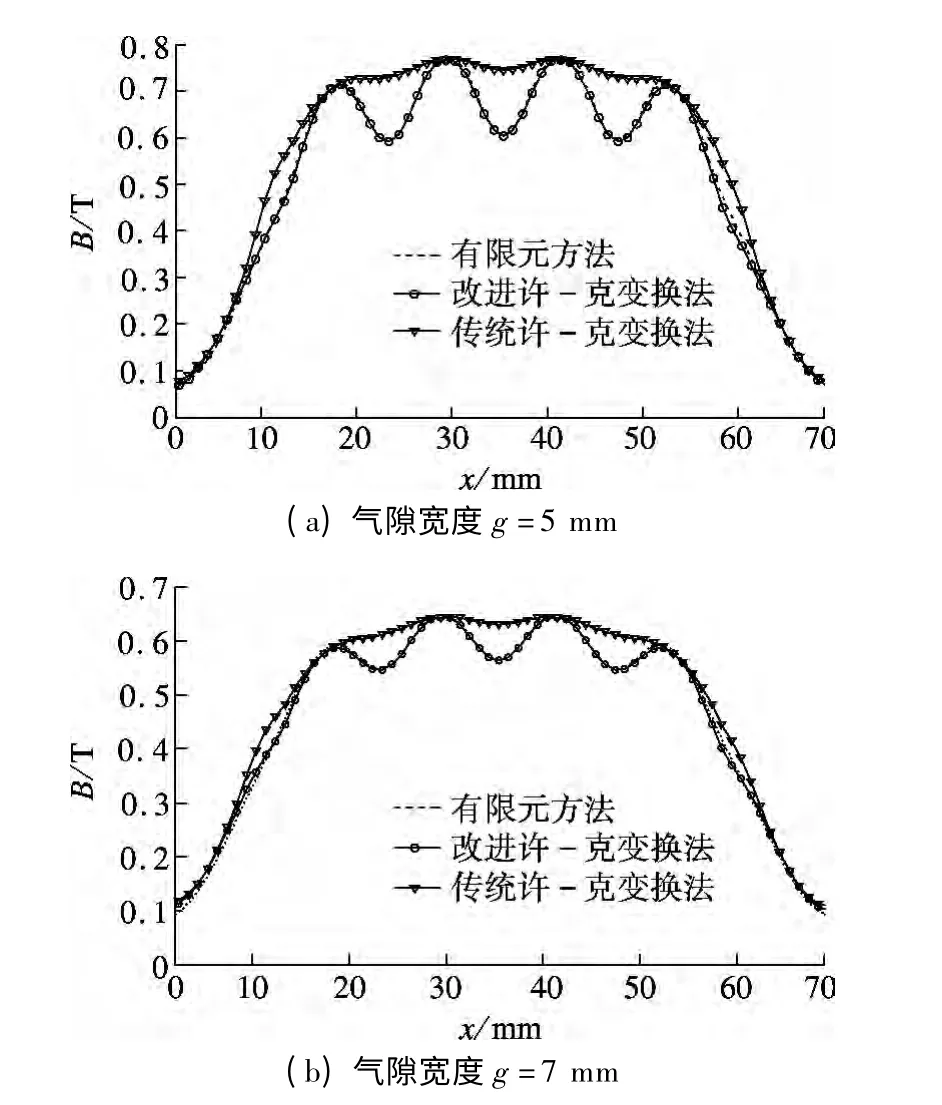
图4 气隙磁场分布

2.2 气隙宽度小于初级铁芯齿宽

在矩形开槽永磁直线电机的气隙宽度小于初级铁芯齿宽的情况下，采用改进的许-克变换法、传统的许-克变换法和有限元法对矩形开槽圆筒型永磁直线电机一个极距气隙磁场分布进行计算，结果如图5所示.由图可见，改进的许-克变换法与有限元法的计算结果误差较小.这表明本文提出的改进许-克变换方法对于永磁直线电机的初步设计和优化是有效可行的.

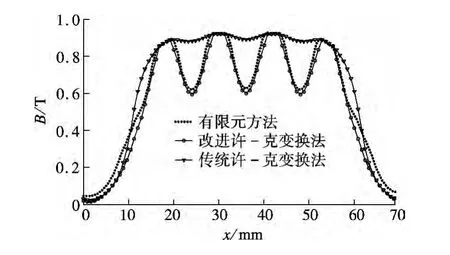
图5 气隙宽度小于初级铁芯齿宽时的气隙磁场分布(g=3 mm)

3 样机试制

利用改进的许-克变换解析计算方法获得矩形开槽永磁直线电机气隙磁场分布后，可以实现永磁直线电机结构的初步优化设计.课题组在结构优化设计的基础上，试制了一台短次级矩形开槽圆筒型永磁直线发电机，其样机如图6(a)所示.该样机的相数为3，永磁体厚度为6 mm，极距为45 mm，气隙宽度为2 mm，齿宽为5 mm，槽宽为7 mm.

图6(b)是通过改进许-克变换解析计算方法和有限元方法获得的一个极距气隙磁场分布.其比较结果表明，一个极距的两端气隙磁场分布略有差异.这种差异的主要原因是由于较小的气隙宽度(g=2 mm)增强了永磁体的端部效应，从而导致初级铁芯和次级铁芯的磁通密度分布发生局部饱和.由此可知，随着气隙宽度的减小，磁通在永磁直线电机的径向方向有效面积也随之减小，初级铁芯和次级铁芯会出现局部饱和的情况.

样机的反电动势实验波形和有限元仿真计算波形如图6(c)所示.通过二者的比较可知，有限元仿真计算的反电动势波形几乎与实验测量的反电动势波形保持一致，证实了本文提出的改进许-克变换解析计算方法对于永磁直线电机的初步设计和性能分析是有效可行的.

4 结语

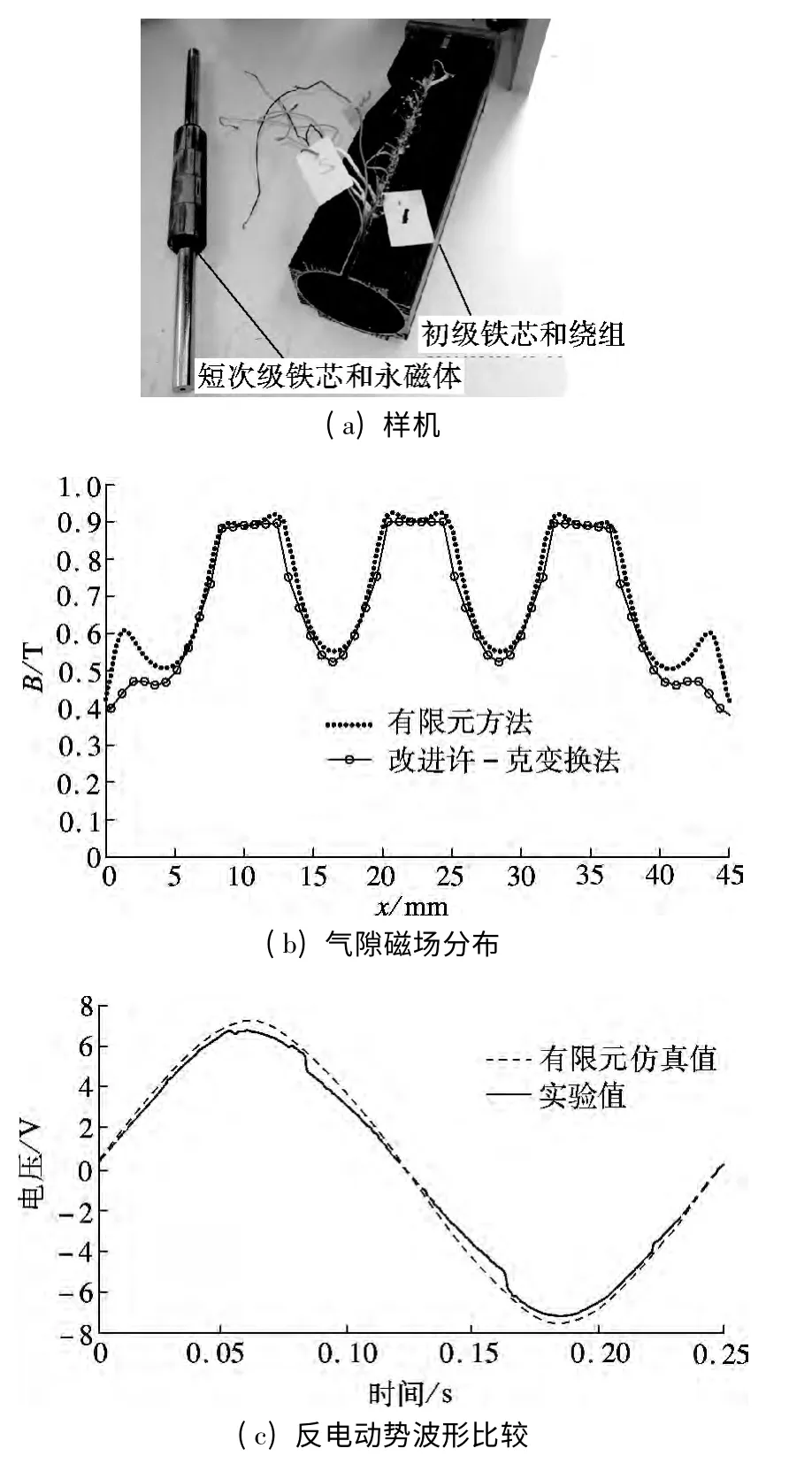
图6 样机的试制和实验

本文在传统的许-克变换法基础上，提出了一种改进的许-克变换解析计算方法.该解析计算方法不仅考虑了永磁直线电机的合成气隙宽度，还考虑了永磁直线电机的实际气隙宽度.此外，由于永磁体端部效应的影响，本文还对永磁体之间的气隙磁导分布函数作了修正.通过解析计算和有限元仿真，证实了该解析计算方法的可行性，从而为矩形开槽永磁直线电机的初步结构优化和设计提供了参考依据.

References)

［1］ Mahmoudi A，Rahim N A，Ping H W.Axial-flux permanent-magnet motor design for electric vehicle direct drive using sizing equation and finite element analysis［J］.Progress in Electromagnetics Research，2012，122:467-496.

［2］ Terata M，Fujii N.Permanent magnet linear synchronous motor with high air-gap flux density for transportation［J］.International Journal of Applied Electromagnetics and Mechanics，2012，39(1/2/3/4):997-1003.

［3］ 李志强，胡笳，祝丽芳，等.同步发电机有限元磁场计算中端点量迭代的改进算法［J］.电工技术学报，2008，23(12):35-41.Li Zhiqiang，Hu Jia，Zhu Lifang，et al.An improved iterative algorithm for terminal quantity of synchronous generator in FEM magnetic field［J］.Transactions of China Electrotechnical Society，2008，23(12):35-41.(in Chinese)

［4］ 罗炜，李志强，罗应立.用于平滑处理的卷积运算及其在有限元磁场分析后处理中的应用［J］.电工技术学报，2009，24(4):1-5.Luo Wei，Li Zhiqiang，Luo Yingli.Smoothing convolutions and applications in postprocessing of finite element analysis of magnetic field ［J］.Transactions of China Electrotechnical Society，2009，24(4):1-5.(in Chinese)

［5］ 何山，王维庆，张新燕，等.双馈风力发电机多种短路故障电磁场仿真研究［J］.电力系统保护与控制，2013，41(12):41-46.He Shan，Wang Weiqing，Zhang Xinyan，et al.Simulation study of multiple short-circuit fault electromagnetic field about DFIG in wind power［J］.Power System Protection and Control，2013，41(12):41-46.(in Chinese)

［6］ 崔鹏，张锟，李杰.基于许-克变换的悬浮电磁铁力与转矩解析计算［J］.中国电机工程学报，2010，30(24):129-134.Cui Peng，Zang Kun，Li Jie.Calculation of electromagnetic force and torque of suspension electromagnet based on schwarz-christoffel transform ［J］.Proceedings of the CSEE，2010，30(24):129-134.(in Chinese)

［7］ Boughrara K，Zarko D，Ibtiouen R，et al.Magnetic field analysis of inset and surface-mounted permanent magnet synchronous motors using schwarz-christoffel transformation［J］.IEEE Transactions on Magnetics，2009，45(8):3166-3178.

［8］ Krop D C J，Lomonova E A，Vandenput A J A.Application of schwarz-christoffel mapping to permanentmagnet linear motor analysis［J］.IEEE Transactions on Magnetics，2008，44(3):352-359.

［9］ Gysen B L L，Lomonova E A，Paulides J J H，et al.Analytical and numerical techniques for solving Laplace and Poisson equations in a tubular permanent magnet actuator:part ⅡSchwarz-Christoffel mapping［J］.IEEE Transactions on Magnetics，2008，44(7):1761-1767.

［10］ 卢晓慧，梁加红.表面式永磁电机气隙磁场分析［J］.电机与控制学报，2011，15(7):14-20.Lu Xiaohui，Liang Jiahong.Air gap magnetic field analysis of surface-mounted permanent magnet motors［J］.Electric Machines and Control，2011，15(7):14-20.(in Chinese)

［11］ 赵镜红，张俊洪，方芳，等.径向充磁圆筒永磁直线同步电机磁场和推力解析计算［J］.电工技术学报，2011，26(7):154-160.Zhao Jinghong，Zhang Junhong，Fang Fang，et al.Analytical calculation of magnetic field and thrust force in radial magnetized tubular permanent magnet linear synchronous motor［J］.Transactions of China Electrotechnical Society，2011，26(7):154-160.(in Chinese)

［12］ 王淑红，熊光煜.永磁直线同步电动机气隙磁场及磁阻力分析［J］.煤炭学报，2006，31(6):824-828.Wang Shuhong，Xiong Guangyu.Analyses of the airgap magnetic field and detent force of permanent magnet linear synchronous motor［J］.Journal of China Coal Society，2006，31(6):824-828.(in Chinese)

［13］ Wang J B，Howe D，Jewell G W.Analysis and design optimization of an improved axially magnetized tubular permanent-magnet machine［J］.IEEE Transactions on Magnetics，2004，19(2):289-295.

［14］ 卢玉峰，刘西民.复变函数［M］.北京:高等教育出版社，2007:152-183.

［15］ 胡之光.电机电磁场的分析与计算［M］.北京:机械工业出版社，1989:38-45.

［16］ 张颖.永磁同步直线电机磁阻力分析及控制策略研究［D］.武汉:华中科技大学机械科学与工程学院，2008:20-21.