基于LOB的辐射源无源定位算法对比研究

徐万里，刘 准

(装甲兵工程学院信息工程系，北京100072)

利用无源传感器测量并实现辐射源的定位是军事和民用领域的一个常见问题，现代信息化战争的焦点是信息的获取和处理，处理的基本问题是对目标进行定位和识别。在定位装备实际测量过程中，得到的原始数据总会伴有噪声和误差，采用哪种定位算法来处理测得的数据，能更好地减小噪声和测量误差对目标位置估计值的影响，成为研究此类定位问题的重点［1］。

现代定位技术的主要算法有三角定位法、二次定位法和单站定位法等，而其核心技术是基于辐射源方位线(Lines Of Bearing，LOB)或到达时差(Time Difference Of Arrival，TDOA)。基于 LOB的定位算法主要有 Pages-Zamora定位算法［2］、布朗定位算法［2］、概率定位算法［3］、模糊定位算法［4］。本文首先分析了以上4种算法的原理，计算了运算量;然后提出了一种基于LOB的融合-迭代定位算法，并与以上4种算法进行了蒙特卡罗仿真对比实验，比较了5种算法的定位性能。

1 基于LOB的三角定位原理

为了便于比较基于LOB的辐射源定位的诸多算法的性能，同时不失一般性，可考虑如图1所示的情况［5-6］。

图1 中有N 个测向观站点 (xi，yi)，i=1，2，…，N，N个测向角度φi和1个辐射源目标点(xT，yT)。在没有噪声和测量误差的理想情况下，通过多组测向数据所求得的辐射源目标坐标会重合为一点。然而在实际测量中，测得的方位线总会受到噪声和测量误差的影响，其对位置估计结果的影响体现在多条方位线不交于一点。因此，采用三角定位原理的定位算法需要解决的问题就是:利用多条方位线及其产生的多个交点，计算出目标点的最佳估计值。

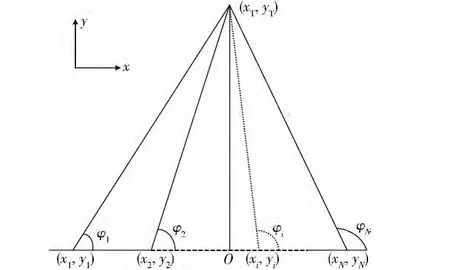
图1 三角定位原理

2 Pages-Zamora定位算法

Pages-Zamora定位算法是基于向量关系的定位方法，其几何原理如图2所示。

图2 Pages-Zamora定位算法原理

根据图2中的向量关系有

式中:di为观测站i与被测目标之间的距离;vi为单位方向向量，可表示为 vi=(cosφi，sinφi)T。

采用如下方法将距离di从式(1)中消去:

由式(2)可得

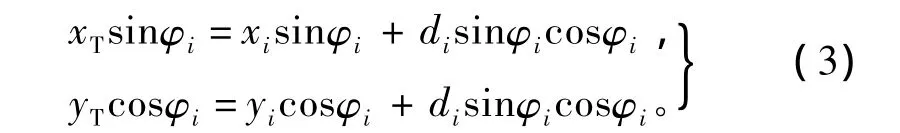
将式(3)两式相减得

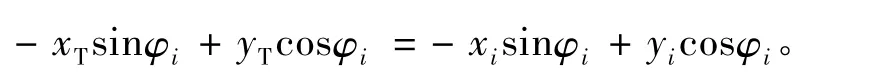
对所有的站点信息进行上述处理，可得如下矩阵形式的方程组:

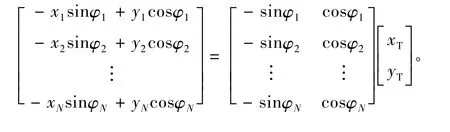
或记为如下形式:

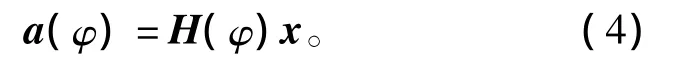
式(4)的最小二乘解为

利用N个观测站对辐射源目标进行测向时，完成1次Pages-Zamora定位算法的运算，需进行(16N+8)次乘/除法和(11N+4)次加/减法。

3 布朗最小二乘定位算法

布朗定位算法是基于偏离距离的定位方法，其基本思想是使所求得的目标位置估计值到各条方位线距离的平方和最小化［7］。图3为布朗最小二乘定位算法原理。

图3 布朗最小二乘定位算法原理

根据图3可得总偏离距离的平方和为

令D关于xT和yT的一阶偏导数为0，即得到使总偏离距离平方和最小化的xT和yT:

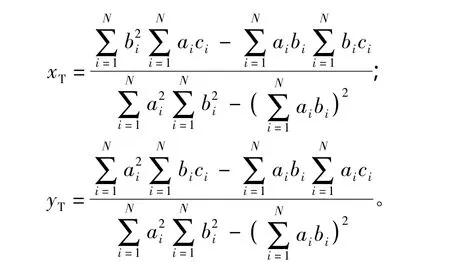
图3中观测站i的偏离距离可表示为

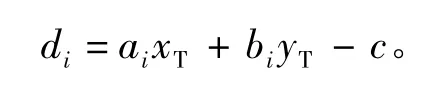
表示为矩阵的形式:

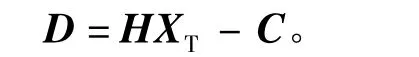
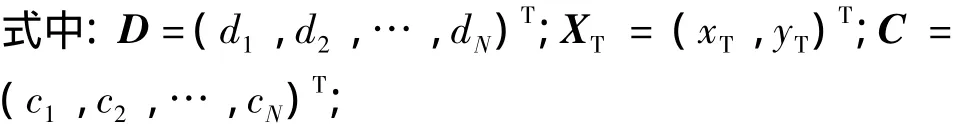
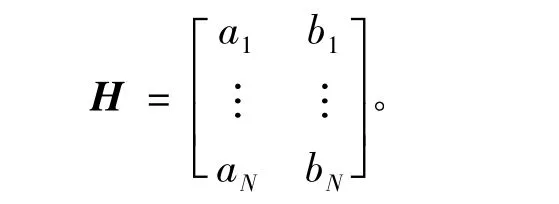
目标方向向量XT的最小二乘估计为

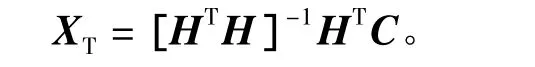
利用N个测向观测站对定位目标进行测向时，每完成1次布朗定位算法，需进行(11N+10)次乘/除法和(6N+4)次加/减法。

4 概率定位算法

观测站测量结果中的误差是由多种因素的综合作用形成的，依据统计的观点，可以认为该误差服从正态分布［3］。设测量结果为W，W0为任意一个具体的测量结果，则可以用概率密度函数来描述二者的关系，即

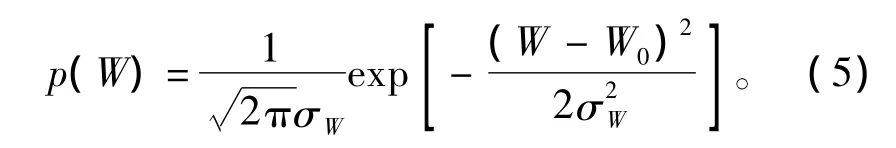
然后，需要将上述非线性问题线性化。设测量W对应一个子集，该子集的坐标点与测量值之间的关系如下［8-9］:

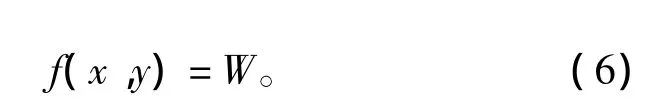
将式(6)在(x0，y0)处进行泰勒级数展开，保留一阶项，舍弃高阶项，可得［9］

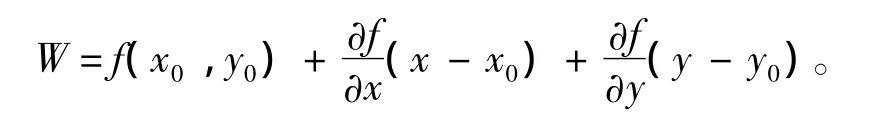
于是，式(5)可化为

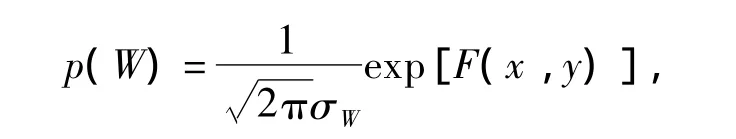
式中:

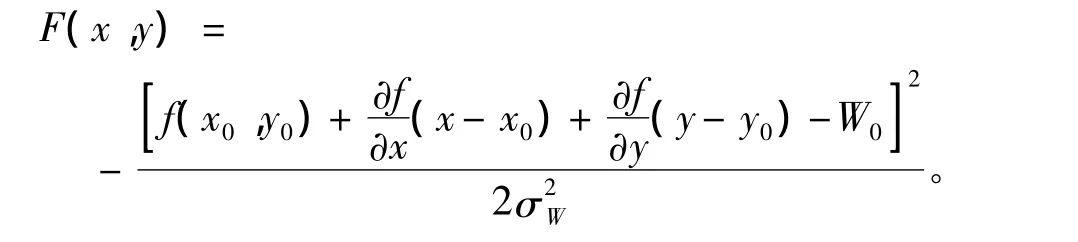
F(x，y)是一个二次多项式，可将其记为如下标准形式［9］:

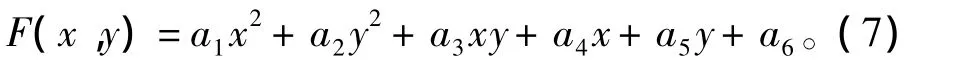
在这个问题中，求解定位点估计值的过程就是求解概率密度最大的过程［8］。由于所有单个测量的概率密度函数都是指数函数，因此他们相乘得到的多个测量的总概率密度函数也是一个指数函数，其指数是单个概率密度函数的指数之和［8-9］。那么，它们的和F(x，y)也将是关于x，y的二次多项式，可以继续使用式(7)来表示。将式(7)分别对x，y求偏导，令偏导数为0，可以得到求解目标点估计值的方程组:

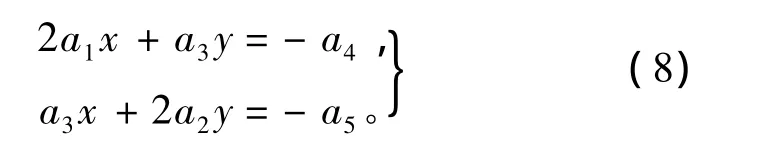
由式(8)可求出目标点估计值的解为

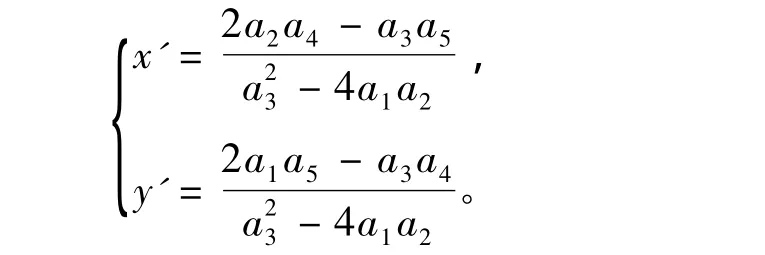
利用N个测向观测站对辐射源目标进行测向时，完成1次概率定位算法的运算，需进行(30N+13)次乘/除法和(17N+6)次加/减法。

5 模糊定位算法

从N个观测站中任取2个观测站点，分别记为(xi，yi)和 (xj，yj)，i，j=1，2，…，N ，由这 2 个观测站测得的数据可求得交点坐标(xij，yij):

将测向信息两两组合，可计算得到C2N个交点，这些交点较为集中地分布在目标点周围，模糊定位算法利用各交点的相关程度来估计目标点的坐标［10］。与概率定位算法相似，可以认为测量误差服从正态分布。

数定义为

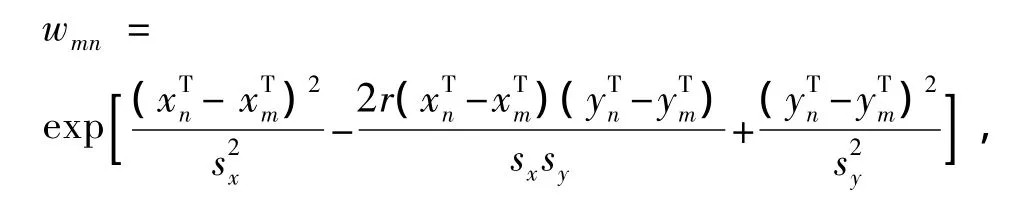
式中:sx、sy分别为C2N个交点的x、y坐标基于样本均值计算出的标准差;r为C2N个交点的x、y坐标基于sx、sy的相关系数。

定义各点对本身的隶属度wmm=1，交点，)与交点，)的相关程度越大，则其隶属度wmn越大。对于任意一个交点()，都有个隶属度 wmn，m，n=1，2，…，由此可得到一个×的模糊矩阵:

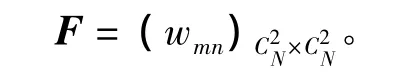
式中:an为交点(xTn，yTn)对各交点的隶属度之和。an越大，其对各交点的总体相关程度越高，因此，使an取得最大值的交点的坐标可被视为目标点的估计值。

利用N个观测站对目标点进行测向时，每完成1次模糊定位算法的运算，需进行(11N4-22N3+41N2-30N+40)/8次乘/除法和(2N4-4N3+19N2-17N-12)/2次加/减法。当N较大时，可以采用11N4/8次乘/除法来衡量模糊定位算法的计算量。

6 融合-迭代算法

依据数据融合的思想，本文提出一种基于交点坐标融合的目标点估计方法，称为融合-迭代定位算法。其基本思想是:依据LOB得到的一组交点，根据各交点到估计值的距离赋予相应的权重值，距离估计值越近，权重越大，反之则越小;然后将交点进行加权融合并迭代运算，逐步逼近目标值。

设(x0，y0)为目标的初始估计值，通过三角定位原理计算所有观测站观测辐射源的LOB两两相交的交点 (xij，yij)，i，j=1，2，…，N ，且 i ＜ j。

计算每个交点 (xij，yij)与目标估计值(x0，y0)的距离:

根据dij来确立每个(xij，yij)所对应的权重值:

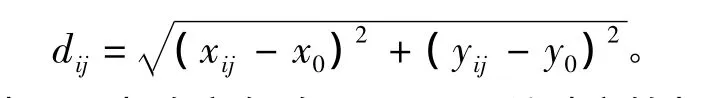
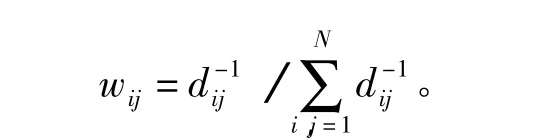
计算加权融合后的估计值(xf，yf):

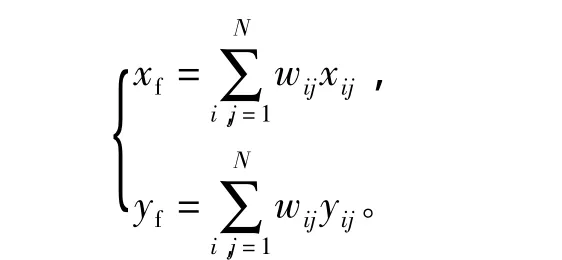
其中 i＜ j，经迭代逐步逼近 (xT，yT)。

利用N个测向观测站对定位目标点进行测向时，每完成1次融合-迭代定位算法，需进行(N4-2N3+29N2-28N)/4次乘/除法和(N4-2N3+29N2-28N-8)/4次加/减法。

7 仿真实验

实验中辐射源(xT，yT)位置设定和观测站的布站位置按照图1给定。辐射源位于y轴上，11个观测站等距地分布在x轴上。采用蒙特卡罗［11］仿真实验产生100组随机测向角度，用数据的均值和圆概率误差(Circular Error Probability，CEP)对各种算法的性能进行比较。

设定位估计的协方差矩阵为

如果误差服从正态分布，那么误差区域是一个椭圆，称为概率误差椭圆(Elliptical Error Probability，EEP)，其半长轴a和半短轴b的计算公式分别为

式中:C=-2ln(1-Pe)，其中Pe为目标位于该误差椭圆中的置信度［7］。

半长轴a相对于x轴的倾角θ为

用R表示CEP，则

采用这种方法求得的圆半径误差在10%以内［12］。

设辐射源位置固定不变，坐标为(0，100)，在x轴的区间［-50，50］中，等距离布置上11个观测站，对目标进行测量，假设观测站测向角度误差为2°。(σx，σy)为定位结果(xT，yT)的标准差，误差为定位结果相对于辐射源坐标(0，100)的距离。定位数据记录如表1所示。

表1 仿真定位结果

由表1可知:Pages-Zamora定位算法与布朗定位算法估计结果完全一致，同属最小二乘级精度，但布朗定位算法的运算量更小;概率定位算法的精度较低，这是因为它采用线性截断，直接丢弃了非线性项，其计算量与Pages-Zamora定位算法相近;基于隶属度函数的模糊定位算法没有引入截断误差，其定位误差小于以上3种算法，但是该算法高度依赖于测向角度的精度，稳定度差导致CEP增大，而且该算法计算量较大;融合-迭代定位算法的精度最高，这是由于它重用均值附近的测量点，而最小二乘法强调的是总体误差最小，同时该算法计算量的增大在可接受范围之内。

8 结论

本文分析了Pages-Zamora定位算法、布朗定位算法、概率定位算法、模糊定位算法的原理，并计算出其运算量，在此基础上提出了基于LOB的融合-迭代定位算法，然后对这5种算法进行了蒙特卡罗仿真对比实验，比较了其定位性能。实验结果表明:融合-迭代算法最能反映数据自身的分布规律，是可取的高性能无源定位算法。

［1］ 孙仲康，郭福成，冯道旺．单站无源定位跟踪技术［M］．北京:国防工业出版社，2008:12-14．

［2］ Poisel R A．电子战目标定位方法［M］．北京:电子工业出版社，2008:26-94．

［3］ 胡来招．无源定位［M］．北京:国防工业出版社，2004:41-48．

［4］ 徐万里，聂辉宇．辐射源信号模糊定位算法［J］．四川兵工学报，2011，32(6):57-59．

［5］ Dogancay K．Bearings-only Target Localization Using Total Least Squares［J］．Signal Processing，2005(85):1695-1710．

［6］ Dogancay K．On the Bias of Linear Least Squares Algorithms for Passive Target Localization［J］．Signal Processing，2004(84):475-486．

［7］ Poisel R A．Introduction to Communication Electronic Warfare Systems［M］．Norwood，MA:Artech House，2002:384-388．

［8］ 徐志刚，田增山，田世君．基于概率的无源定位算法［J］．信息技术，2005(12):74-77．

［9］ 佘青松．无源探测定位技术研究［D］．成都:电子科技大学，2007．

［10］ 杨纶标，高英仪．模糊数学原理及应用［M］．广州:华南理工大学出版社，2005:7-11．

［11］ 贺骁，刘芸江，刘梅．一种蒙特卡罗方法的改进方案［J］．中国科技论文，2014(1):71-75．

［12］ Foy W H．Position-location Solutions by Taylor-series Estimation［J］．IEEE Transactions on Aerospace and Electronic Systems，1976，AES-12(2):187-194．