轴向剪切条件下功能梯度圆柱形复合材料的界面开裂问题研究

李永东，熊 涛，张 男

(1．装甲兵工程学院机械工程系，北京100072;2．装甲兵工程学院基础部，北京100072)

层合柱是工程中广泛应用的一类典型复合材料。最简单的传统层合柱由2种不同的均匀材料粘接而成，在外载荷作用下，其界面附近往往存在应力集中。当应力集中程度很高时，界面甚至可能出现开裂［1］。在这方面，学术界早已达成共识，认为此类界面出现应力集中甚至开裂的主要原因是材料性能参数在界面处不连续［2］。近年来，工程中设计制造出了功能梯度层合柱，其不同层的材料性能参数在界面处连续过渡，因而具有更高的抗界面开裂能力［3-4］。制造功能梯度层合柱的目的除了提高界面抗断裂能力外，还可能是为了改善层合柱的某种性能。例如:在受摩擦作用的轴段表面喷涂功能梯度耐磨涂层，不但可以改善涂层与轴体之间的结合性能，还可以提高该轴段抵抗摩擦的能力。相对于传统均匀材料而言，功能梯度材料的一大优势就是其可设计性。因此，为了提高功能梯度层合柱的界面结合性能，有必要对其开展断裂力学研究，利用断裂力学分析结果对其进行结构与性能优化设计。笔者等［5］对外覆功能梯度涂层的实心圆柱开展了断裂力学分析，研究了径向正应力作用下的Ⅰ-Ⅱ混合型界面裂纹问题，得到了该圆柱的外覆功能梯度涂层优化设计结果。对实际的层合柱界面而言，除了受径向正应力作用外，还可能会受轴向剪切作用。在轴向剪切条件下，功能梯度层合柱的界面具有怎样的断裂力学行为，如何对层合柱的功能梯度层进行优化设计，在文献［5］的基础上，本文继续研究轴向剪切条件下外覆功能梯度涂层实心圆柱界面的开裂问题，从材料性能参数分布和几何尺寸选取2方面寻求较优的设计结果。

1 理论模型

图1为功能梯度圆柱形复合材料界面开裂的理论模型。该复合材料置于无限大刚性基体中，内层为均匀实心圆柱，外层为功能梯度涂层，涂层内、外半径分别为r1和r2。在界面上有一条圆心角为2α的弧形裂纹，以复合材料横截面圆心o为原点，令x轴通过裂纹中心，分别建立直角坐标系和相应的极坐标系，则裂纹所占据的极角范围为［-α，α］，且整个结构关于x轴对称。

假设圆柱和涂层分别为各向同性线弹性材料，则在轴向剪切条件下其本构方程可统一表示为

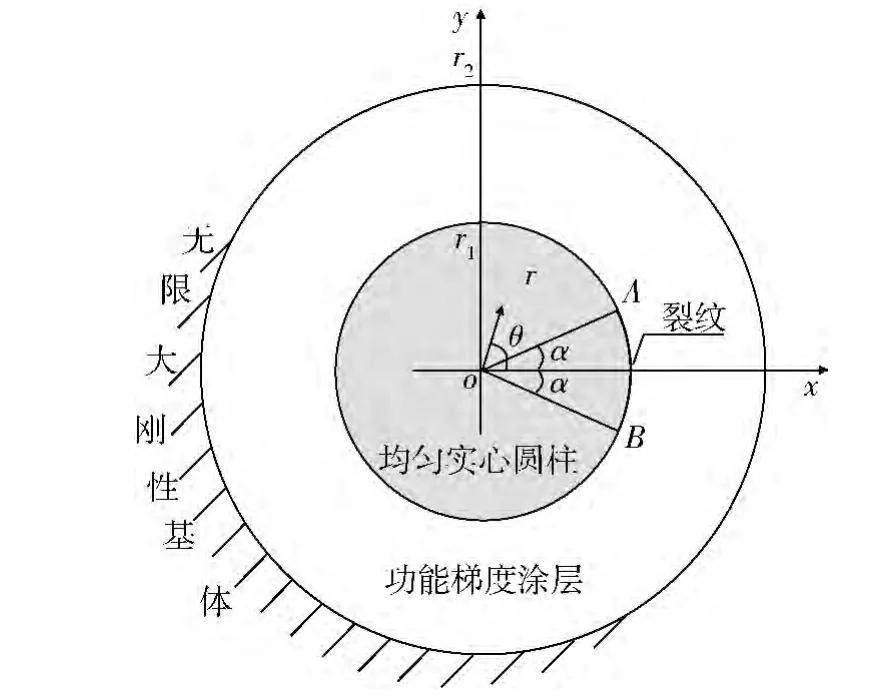
图1 功能梯度圆柱形复合材料界面开裂的理论模型

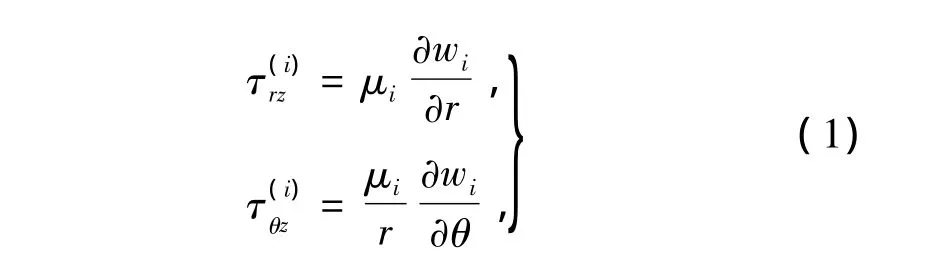
式中:i=1，2，其中1用于标志圆柱中的量，2用于标志涂层中的量;τ为切应力;w为轴向位移;μ为剪切模量。圆柱为均匀线弹性材料，其剪切模量μ1为常数。涂层为功能梯度材料，其剪切模量沿厚度方向连续变化，假设为径向坐标r的幂函数［5］，则

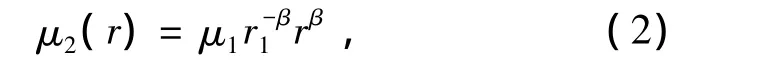
式中:β为涂层的非均匀性参数，且无量纲。

轴向剪切条件下圆柱和涂层的平衡方程为

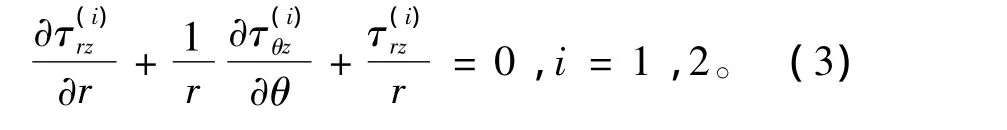
将式(1)代入式(3)，并考虑式(2)，可得控制方程为

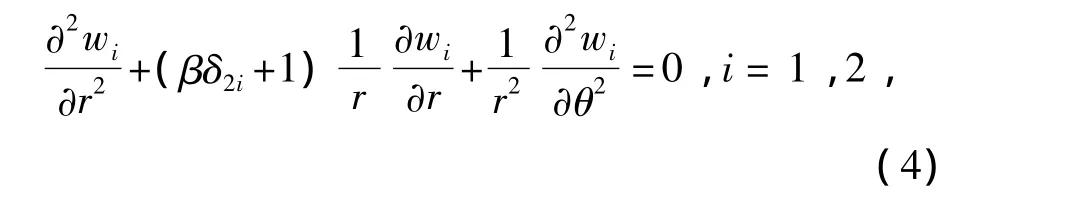
式中:δ2i为Kronecker符号，当其2个下标相同时，值取1，否则取0。

在轴向剪切条件下，假设裂纹面上的等效切应力为-τ0。由于图1所示的断裂问题关于x轴对称，所以下面仅研究复合材料横截面的上半部分。该问题的边界条件和连续性条件为

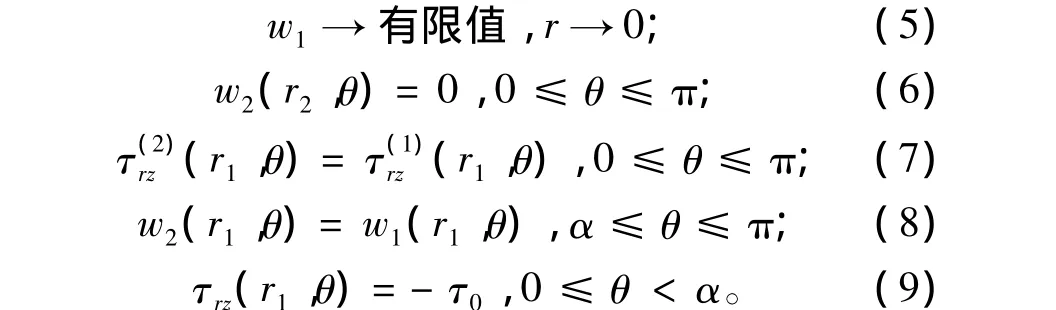
2 奇异积分方程

考虑问题的对称性，利用分离变量法［6］求解式(4)，可得满足式(5)中定解条件的位移场的解为

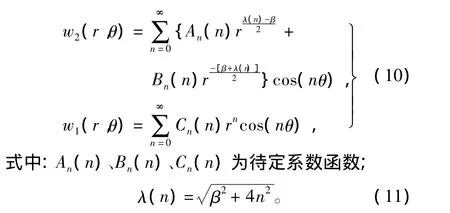
将式(10)代入式(1)可得应力场(略)。然后，将位移场和应力场代入式(6)、(7)，可得

3 数值计算与讨论

本文中，假设r1=30 mm，μ1=4．4 ×1010N/m2。在具体求解无量纲应力强度因子的数值之前，需首先明确其计算精度。

3．1 计算精度

无量纲应力强度因子的计算精度主要取决于无量纲核函数R(ϑ，ζ)的计算精度和求积节点数m的取值。

本文中，R(ϑ，ζ)为无穷级数，其无穷求和区间［1，+∞)在数值计算中被截断为有限区间［1，N］，因此，R(ϑ，ζ)的计算精度主要取决于N的取值。具体计算中需根据 R(ϑ，ζ)的收敛性选取N。当ζ =-1，ϑ =cos(3π/40)，α = π/6，β =2，r2/r1=1．2时，N对R(ϑ，ζ)收敛误差的影响如表1所示。可见:N=2 500时，R(ϑ，ζ)的收敛误差已小于1．0×10-5。在后续计算中，以 1．0 ×10-5作为 R(ϑ，ζ)的收敛误差，反过来确定具体计算中所需的N值。

求积节点数m的值需根据无量纲应力强度因子的收敛性来选取。当 N=2 500，ζ=-1，ϑ =cos(3π/40)，α = π/6，β =2，r2/r1=1．2时，m 对无量纲应力强度因子收敛误差的影响如表2所示。可见:当m≥20时，无量纲应力强度因子的收敛误差已小于1．0 ×10-4。在后续计算中，以1．0 ×10-4作为无量纲应力强度因子的收敛误差，反过来确定具体计算中所需的m值。值得注意的是:为了减小计算中的累积误差［3］，这里设定 R(ϑ，ζ)的收敛误差小于无量纲应力强度因子的收敛误差。

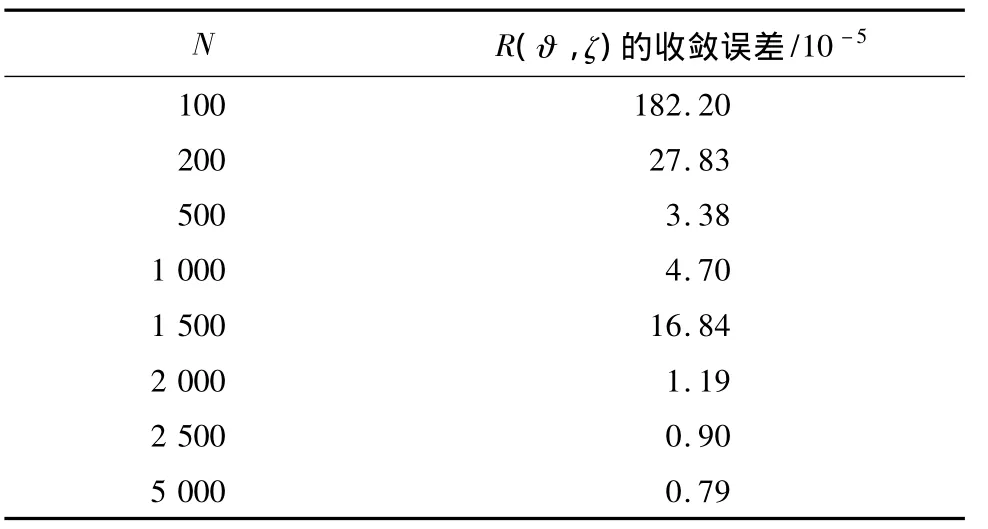
表1 N对R(ϑ，ζ)收敛误差的影响

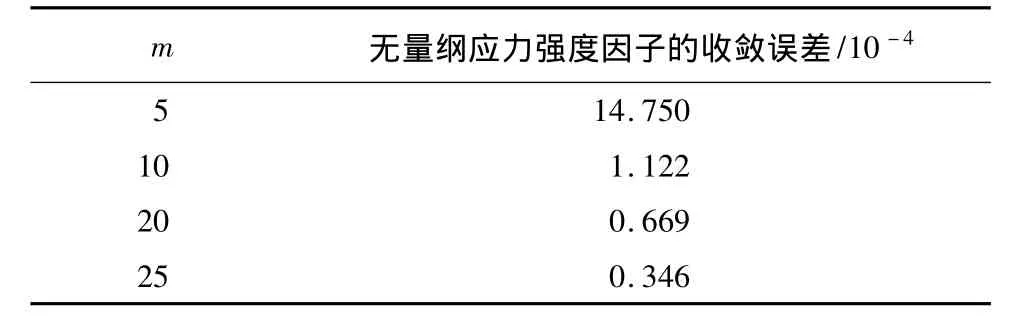
表2 m对无量纲应力强度因子收敛误差的影响

3．2 几何参数对无量纲应力强度因子的影响

本节主要讨论在中心圆柱半径r1给定的条件下，功能梯度涂层厚度和裂纹中心角2方面的几何因素对无量纲应力强度因子的影响。分别以r2/r1和α作为相应的几何参数，它们对无量纲应力强度因子的影响规律分别如图2、3所示。

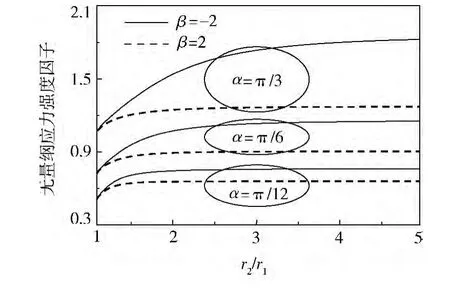
图2 r2/r1对无量纲应力强度因子的影响

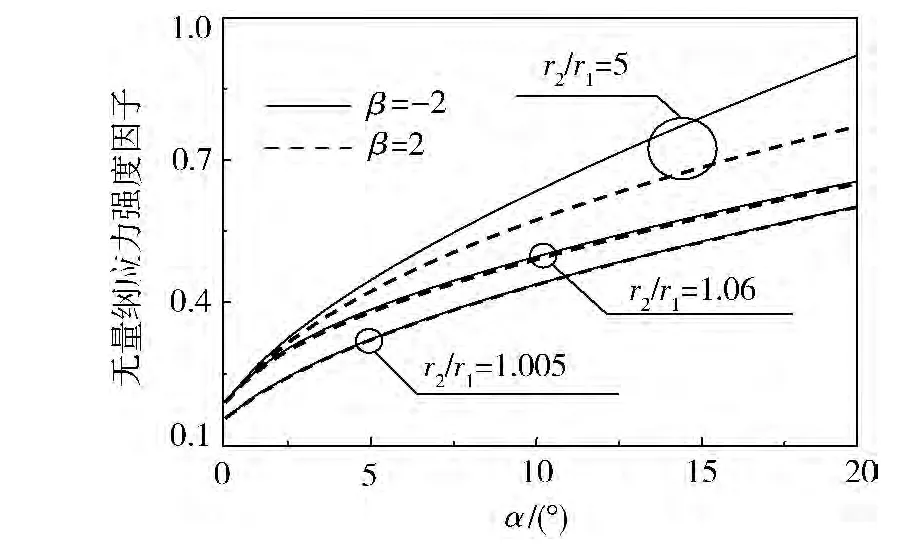
图3 α对无量纲应力强度因子的影响

由图1可知:当r2/r1→1．0时，涂层厚度趋于0;当r2/r1＞1．0时，其值越大，则涂层越厚。由图2可见:随着r2/r1从1．0开始增大，无量纲应力强度因子逐渐增大。这一变化规律是由图1中复合材料的约束方式决定的。由于固定边界对其附近区域内的裂纹存在屏蔽作用［7］，所以，当图1所示的复合材料置于刚性基体之中(即外表面固定)时，涂层越薄，则界面裂纹越靠近固定边界，其所受的屏蔽作用越显著，其无量纲应力强度因子也会越小;反之，无量纲应力强度因子会越大。由此可见:在外表面固定的条件下，图1中的功能梯度涂层宜薄而不宜厚。

由图3可见:1)无量纲应力强度因子随α的增大而增大，在r1给定的条件下，α越大，则界面裂纹越长，在其他条件不变的情况下，裂纹越长，则无量纲应力强度因子越大，这是符合断裂力学规律的;2)涂层厚度不同，无量纲应力强度因子随α变化的剧烈程度也不同，涂层越薄，无量纲应力强度因子随α增大得越缓慢。这再次表明:在外表面固定的条件下，图1中的功能梯度涂层宜薄而不宜厚。

3．3 非均匀性参数对无量纲应力强度因子的影响

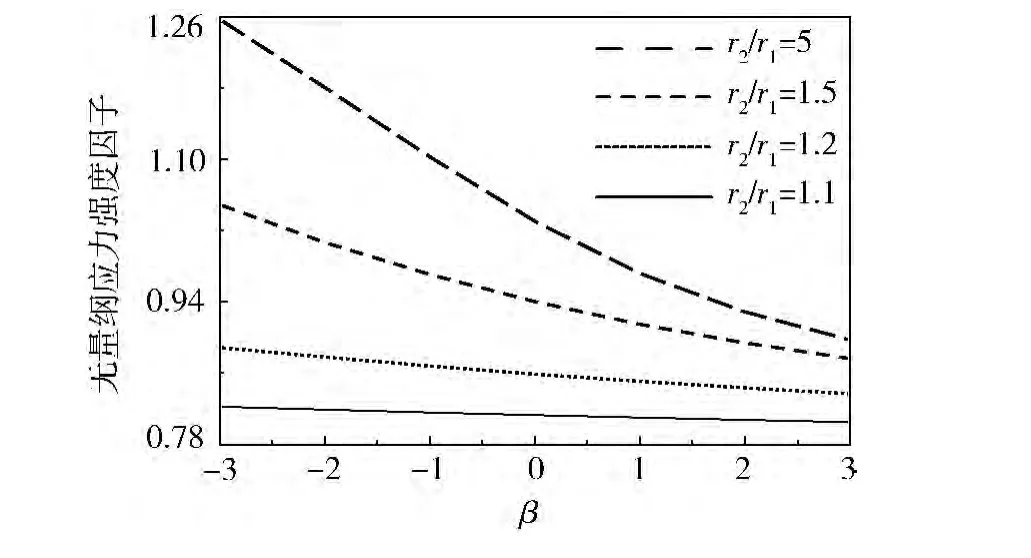
图4 非均匀性参数对无量纲应力强度因子的影响(α=π/6)

当α=π/6，功能梯度涂层的非均匀性参数β对无量纲应力强度因子的影响规律如图4所示，可见:β越大，无量纲应力强度因子越小。根据式(2)，功能梯度涂层的刚度分布情况如图5所示。显然，当β=0时，涂层为均匀材料;当β＞0时，涂层内侧较软而外侧较硬;当β＜0时，涂层内侧较硬而外侧较软。综合分析图4、5，可得出如下结论:当涂层内侧较软而外侧较硬时，界面裂纹的无量纲应力强度因子较低。因此，对于图1所示的外表面刚性固定的功能梯度涂层复合材料，当式(2)中的非均匀性参数选取相对较大的正值时，将有利于减小界面的断裂驱动力。

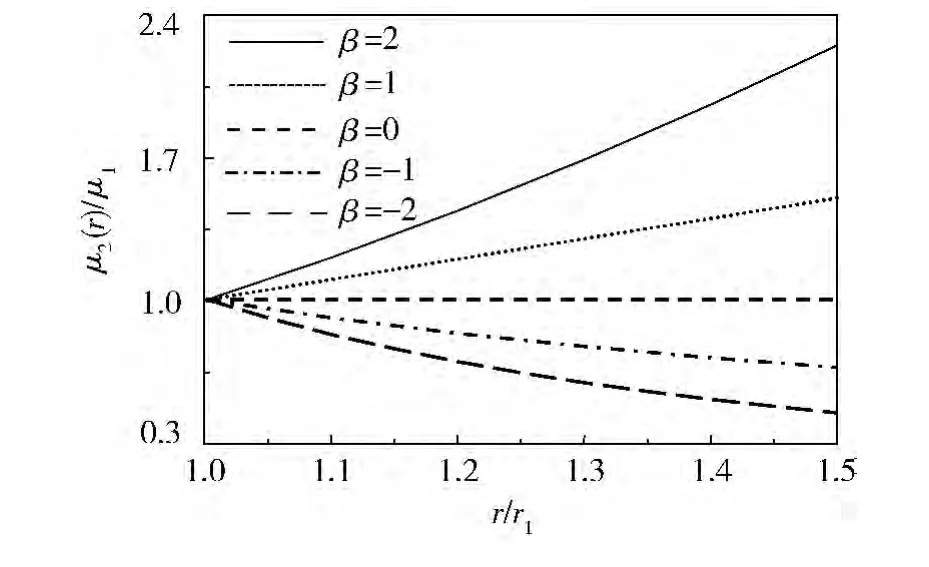
图5 功能梯度涂层的刚度分布情况

4 结论

针对外覆功能梯度涂层的圆柱形复合材料在轴向剪切作用下的界面开裂问题，本文通过断裂力学分析得到了几何参数和非均匀性参数的优化设计结果。即在涂层外表面固定的条件下，以下2种途径都有利于预防界面开裂:1)降低涂层厚度;2)设计内侧软而外侧硬的涂层。本文仅仅研究了静态工况下该类复合材料置入刚性基体中的情况，在实际工程应用中，可能会存在其他的工况条件，其外表面也可能受到其他约束作用。在不同的工况和约束条件下，功能梯度涂层界面将具有不同的断裂力学行为特征，相关规律尚需进一步研究。

［1］ Li Y D，Lee K Y．Fracture Analysis on the Arc-shaped Interface in a Layered Cylindrical Piezoelectric Sensor Polarized along Its Axis［J］．Engineering Fracture Mechanics，2009，76(13):2065-2073．

［2］ Li Y D，Jia B，Zhang N，et al．Dynamic Stress Intensity Factor of the Weak/Micro-discontinuous Interface Crack of a FGM Coating［J］．International Journal of Solids and Structures，2006，43(16):4795-4809．

［3］ Li Y D，Lee K Y．Anti-plane Shear Fracture of the Interface in a Cylindrical Smart Structure with Functionally Graded Magnetoelectroelastic Properties［J］．Acta Mechanica，2010，212(1/2):139-149．

［4］ 李婷，仲政，聂国隽．一种特殊梯度分布的功能梯度圆柱壳的二维分析［J］．力学季刊，2007，28(4):549-556．

［5］ Li Y D，Zhang N，Lee K Y．Fracture Analysis on the Arc-shaped Interfacial Crack Between a Homogeneous Cylinder and Its Coating［J］．European Journal of Mechanics A/Solids，2010，29(5):794-800．

［6］ Li Y D，Lee K Y．Fracture Analysis on the Arc-shaped Interface in a Layered Cylindrical Piezoelectric Sensor Polarized along Its Axis［J］．Engineering Fracture Mechanics，2009，76(13):2065-2073．

［7］ Feng F X，Lee K Y，Li Y D．Multiple Cracks on the Arc-shaped Interface in a Semi-cylindrical Magneto-electro-elastic Composite with an Orthotropic Substrate［J］．Engineering Fracture Mechanics，2011，78(9):2029-2041．