基于加权网络模型的指挥节点重要度评估方法

姜志鹏，张多林，马 婧，王 坤

(1．空军工程大学防空反导学院，陕西西安710051;2．信息保障技术重点实验室，北京100072;3．95876部队，甘肃张掖734100)

指挥网络作为作战指挥体系建设的关键部分，其在攻防对抗中能否正常发挥作用将直接影响战争的胜负。节点在指挥网络中的重要程度不尽相同，节点重要度评估研究有助于发现指挥网络中的薄弱环节，对提高指挥网络体系的可靠性和抗毁性具有重要参考价值［1］。

目前，网络节点重要度评估方法很多，其核心思想主要是:“节点显著性等价于重要性”，“节点删除对网络的破坏性等价于重要性”，“节点重要性不仅取决于自身，还与邻接节点有关”等［2］。其评估方法主要有节点删除法、节点收缩法、拓扑势理论排序法、多属性决策方法等［3-8］;提出的评估指标主要有节点度、临近度、介数、随机行走、凝聚度、接近度等［9-12］;评估范围主要涉及全局、局部、社区重要性等［2，9］;网络类型主要有静态网络、动态网络、加权网络［2，4-8］;评价对象主要涉及计算机网络、犯罪关系网络、病毒传播网络、谣言传播网络、社交网络、科研合作网络、电力网络以及交通网络等。

在军事网络节点重要度研究方面，贾子英等［1］将网络化防空体系的节点重要度分为属性重要度和结构重要度2个维度，并利用模糊偏序关系建立了属性重要度评估模型;王欣等［12］针对指挥信息系统(Command Information System，CIS)的特点，考虑作战任务需求和网络拓扑结构对节点重要度的影响，提出了一种新的CIS节点重要度评估方法;李茂林等［13］在对作战体系结构进行网络描述的基础上，分析了各个指标对节点重要度的影响，并根据网络受损程度选出了最有效的重要性指标。上述方法都能够在相关背景下进行节点重要度评估，对指挥网络节点重要度评估具有很大的启发和借鉴意义，但是这些研究都是基于无权网络模型，且未考虑指挥网络的社区特性，无法深度刻画指挥网络中各个节点之间的关系，不能真实地反映指挥网络的特点。为此，本文考虑指挥网络的任务需求和社区特点，提出了一种利用节点重要度评价矩阵确定加权网络关键节点的方法，并从局部和全局2个方面研究了基于加权网络模型的指挥节点重要度评估方法。

1 指挥网络的加权网络描述与特征分析

1．1 指挥网络的加权网络描述

无权网络反映了节点间的基本连接方式和相互作用，但将实际系统抽象为这种简单的拓扑结构往往会忽略许多客观信息，导致问题描述不全面、不客观，引入加权网络可通过边权值来刻画节点间作用的强弱，从而更客观地描述网络的结构。

首先对指挥网络涉及的术语做如下定义。

定义1:各级指挥机构为网络节点。

定义2:指挥机构之间的信息交流关系为网络的边，并简化为无向单线边。

定义3:节点之间的信息流对作战任务的贡献程度为边的权值(简称边权)。

设G={V，E}，为由n个节点、m条边构成的指挥网络的加权图，其中:V={v1，v2，…，vn}，为节点集合;E={e1，e2，…，em}，为边的集合;

为邻接节点之间边的权值矩阵，wij为邻接节点之间边的权值。

把实际系统抽象为加权网络需要考虑边权的赋值方式，一般有相异权和相似权2种赋权方式［5］，对于相异权，权值越大，表示节点间的距离越大，关系越疏远;对于相似权，权值越大，表示节点间的距离越小，关系越亲密。在加权网络中，由于边权的存在，网络节点间的距离一般不再满足三角不等式，因而导致最短距离路由发生变化。如设节点vi、vk、vj通过权值为wij和wkj的边相连，若采用相异权，节点间的距离可直接取和为dik=wij+wkj;而采用相似权，节点间的距离需要使用调和平均值dik=wijwkj/(wij+wkj)。本文采用相似权，设Xij为节点vi与节点vj之间的信息流对作战任务的贡献度，则边权值wij的取值如下:

本文设定指挥信息的上传、下达均为无向图，则权值矩阵对称，即wij=wji。

1．2 指挥网络的社区特征

复杂网络具有社区特征，即整个网络系统可分为若干个“社区”，每个社区由若干个关系密切的节点构成，因此同一社区内的节点之间的关联相对频繁且紧密，而不同社区之间的关联稀疏且松散。指挥网络系统为追求指挥信息优势最大化，对协同对象和合作范围具有局域选择偏好性，即在小范围内信息相互交流频繁，而在全局范围内的交流相对较少或者交流期望不高，因此整个指挥网络系统的结构具有社区性，这一特征与部队的实际情况是相符的。因为根据不同的作战需求、装备特点、地理条件等，可将作战力量分解为不同的作战集团，各个作战集团又可再分解为若干个小的作战集群，各个作战集群通过上级的指挥与其他作战集群的协同来完成作战任务。因此，作战集群作为一个作战整体，在其内部信息交流频繁，而与外部的信息交流相对较少。整个指挥网络存在如下社区特性:

1)同一社区内(如同一战略、战术、战役单元)的节点之间距离较短;

2)不同社区内(如地理位置或功能不同的作战单元)的节点之间距离相对较大;

3)同一社区内的节点之间信息交流频繁，而与其他社区内的节点之间的信息交流频率较低，即节点通过本社区其他节点的概率较高，而通过其他社区节点的概率较低。

2 评估方法

指挥网络的层次性决定了各个节点的重要程度各不相同。节点重要度与其位置有关，如“非要塞节点”和“要塞节点”，“非末梢节点”和“末梢节点”，“战略节点”和“战术节点”，它们的重要度显然不同。作战指挥网络中节点的特殊性体现在:不同作战任务对节点所在社区的依赖程度不同，导致了不同社区中位置相同的节点其重要度也有差异，因此，指挥网络节点的重要度受网络拓扑结构、作战任务对社区的依赖度2个因素的共同影响。

2．1 作战任务对社区的依赖度

首先对子任务、社区功能子集作如下定义。

定义4:子任务为针对一次作战任务，综合考虑装备特点，按照作战指挥原则，将其细化分解为能由社区直接执行并完成的基本任务序列，称分解后的基本任务为子任务。本文假定一个社区为一个基本作战单元，可独立、直接执行一项子任务。

定义5:社区功能子集(V)为具有相同功能的社区集合，假设同一子集中各社区分别执行同一子任务的效果相同，即彼此间可相互作为备份。

作战任务对社区的依赖度与任务分解、社区功能子集形成、社区选取有关。由于能直接执行子任务的社区所在的功能子集中有其他社区作为备份，且备份越多，某一社区的失效对子任务的损失越小，则任务对这一社区的依赖度也越小。假设作战任务M 可分解为子任务 M1，M2，…，Mn，子任务 Mi对应的社区为lij，功能子集Vi中有ki个备份，则子任务Mi对社区lij的依赖度为

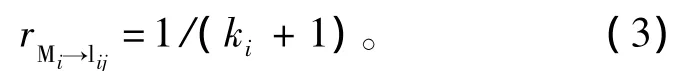
由于子任务对功能子集Vi中所有社区的依赖度相同，对非功能子集中社区的依赖度为0，因此，作战任务M对社区lij的依赖度为

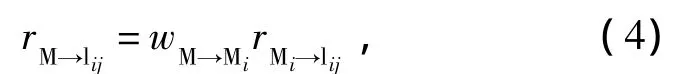
式中:wM→Mi为子任务Mi在任务M中的权重，由子任务Mi对作战任务的重要度确定，假设 M1，M2，…，Mn的重要度依次为 PM1，PM2，…，PMn，则

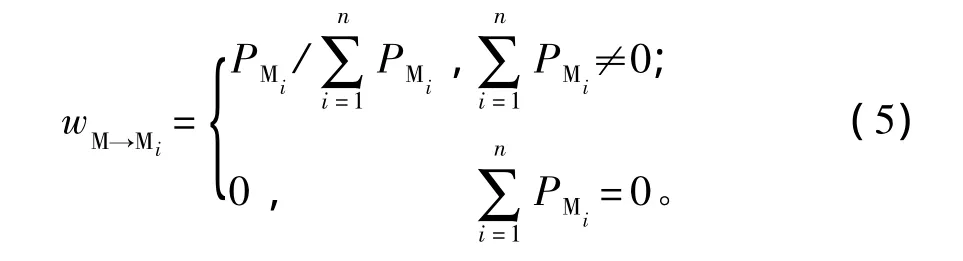
式中:子任务的重要度PM1，PM2，…，PMn可采用文献［14］提出的基于内聚度和粒度的作战任务分解评估方法求解。

2．2 节点相对重要度评价矩阵

网络是由边和节点构成的有机整体，表现在节点与节点间是互相关联的，增加或减少节点都会导致其他节点的点权和载荷发生变化，因此，互联互通的节点之间存在着一定的重要度贡献拓扑关系，其结构为实际网络的一个拓扑映射，本文采用节点重要度贡献矩阵来表示节点之间存在的这种重要度贡献拓扑关系。

文献［15］定义了无权无向网络的节点重要度贡献矩阵，本文在此基础上定义有权无向网络的节点重要度贡献矩阵(Node Importance Contribution Matrix In Weight Networks，NICMIWN)。在有 n 个节点、无自环、有权无向的网络中，若节点vi的点权为si，vi对其每个邻接节点vj的重要性贡献度为wij/si，则当扩展到网络中所有节点时，其对邻接节点的重要性贡献度可以通过加权网络节点相对重要度贡献矩阵来表示:

式中:对角线的Ik为节点vk的重要度初始值。

在作战任务对社区依赖度确定的前提下，可将社区内的指挥网络简化为一般的网络拓扑结构，其节点的重要度取决于节点位置、邻接节点的重要度贡献关系，本文采用点权来构建节点间的重要性贡献关系;由于节点介数(Bn)由节点在网络中的位置决定，因此，可用Bn反映节点vi的位置信息，矩阵HNICMIWN融合Bn后得到节点重要度评价矩阵:

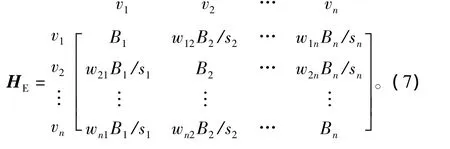
式中:元素HE(ij)表示邻接点vj对节点vi的重要度贡献。由式(7)可以看出:加权网络中某一节点对邻接节点的重要度贡献取决于该节点的介数、点权、边权值。

应用节点相对重要度评价矩阵，综合考虑节点介数、邻接节点重要度贡献，计算节点vi在其所在社区内的相对重要度

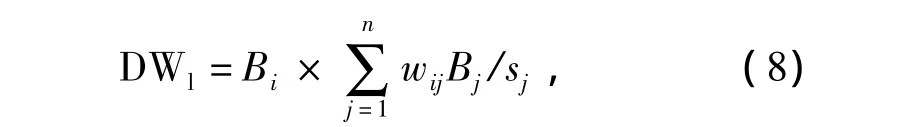
式中:sj为节点vj的点权，

Nj为节点 vj的近邻集合;Bi为节点 vi的介数［16］，

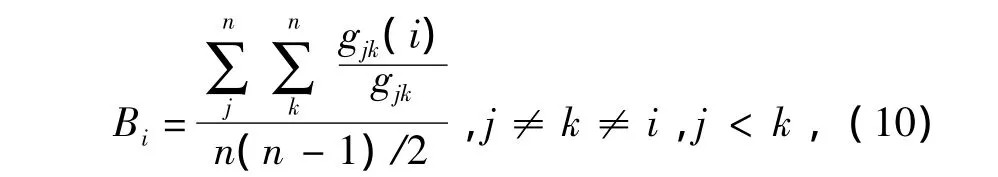
gjk为两节点之间的最短路径数，gjk(i)为经过节点vi的最短路径数，n为节点总数。

2．3 节点全局重要度评价

节点全局重要度评价综合考虑了作战任务对社区的依赖度、节点在所在社区中的相对重要度2方面的因素。评估思路为:1)从全局出发将整个指挥网络分割为一系列社区，给出各社区相对于作战任务的重要度排序，即作战任务对社区的依赖度;2)根据节点在社区的位置信息、邻接节点的重要度贡献关系，给出节点在社区的相对重要度;3)计算节点的全局重要度，即作战任务对社区的依赖度与节点在社区的相对重要度乘积;4)遍历所有节点，得出全部节点的全局重要度。具体步骤如下。

输入，加权图G和给定任务M;输出，节点相对重要度和全局重要度。

1)将作战任务M分解为子任务M1，M2，…，Mn，根据式(3)-(5)计算作战任务对社区的依赖度rM→lij，即社区相对于作战任务的重要度。

2)根据式(6)确定节点在社区内的相对重要度贡献矩阵。

3)根据式(7)确定节点在社区内的相对重要度评价矩阵。

4)根据式(8)计算每个节点vj(j=1，2，…，ni，ni为社区lij内的节点数)在该社区lij内的相对节点重要度DWl。

5)计算所有节点的全局重要度DW(vj)=rM→lij×DWl，j=1，2，…，N，N 为整个网络中所有的节点数。

3 案例分析

以防空部队指挥节点为例，依据现行编制体制，将旅级单位作为一个社区规模，依据装备类型划分社区功能子集，每类装备包含若干社区，假设某一社区lk的指挥网络由4层指挥节点组成，如图1所示。

图1 社区l k加权网络拓扑结构

网络中有10个节点和10条边，根据式(9)、(10)得出网络中各节点的点权和介数，并对应填入节点相对重要度评价矩阵HE中，得出

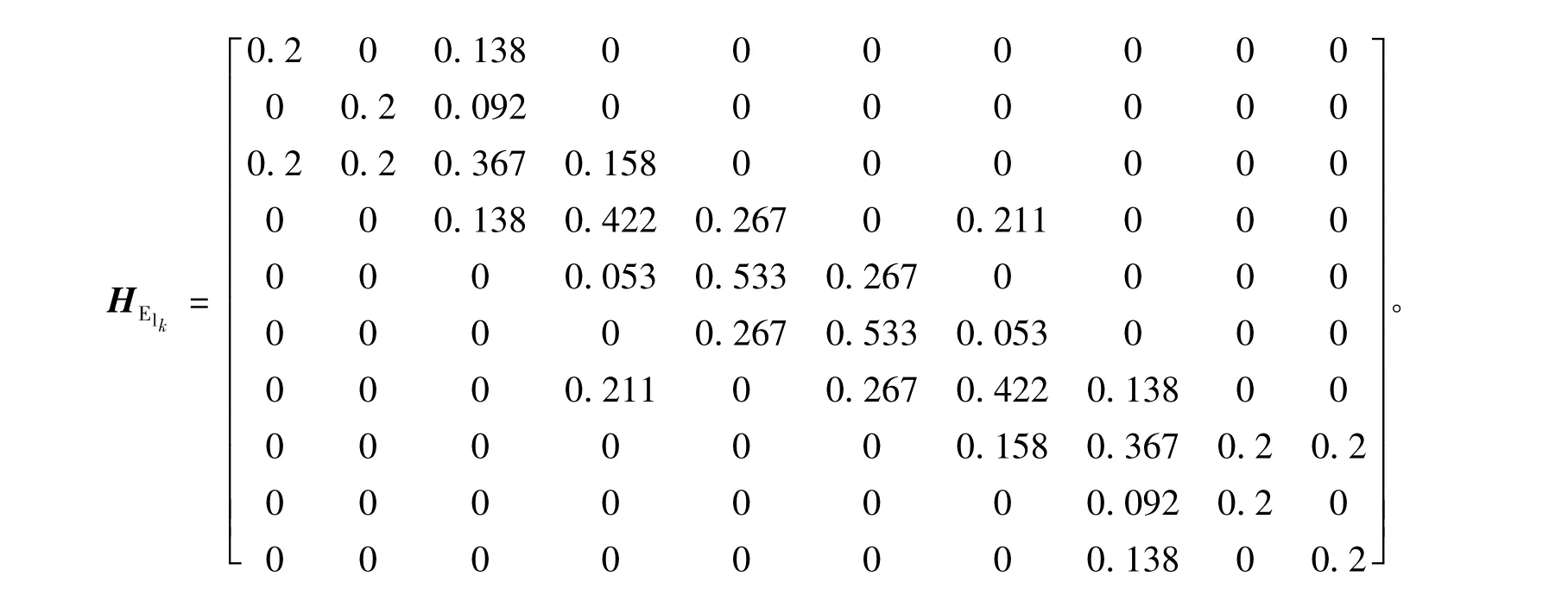
以节点v5为例，通过评价矩阵HElk可得出节点v5在社区lk中的相对重要度DWlk(v5)=0．533×(0．053+0．533+0．267)=0．454 ，同理，可得出其他节点的相对重要度。

表1为采用本文算法计算的社区lk内节点相对重要度评价结果，与介数方法、文献［5］方法、文献［6］方法的评价结果的对比分析，以及社区lk、lg节点全面重要度评估结果。由表1可以看出:1)本文算法与介数方法、文献［6］方法有差异，介数方法不考虑边权，因此无法进一步刻画节点1、2、9、10之间的重要度差异，精度比本文算法稍差，文献［6］方法在节点3、4、5、6、7、8的重要度排序与其他3种算法均有差异，原因在于文献［6］的方法中引入了边重要度系数，给出节点与边系数比值以便重点考察节点重要度，但是边的引入意味着计算结果是将节点、邻边作为整体并与其他整体进行比较，无法将节点剥离出来;2)文献［5］的方法与本文算法的结果一致，得出节点5和节点6为最重要节点，但本文算法不涉及归一化运算、矩阵乘法，运算量相对较小。

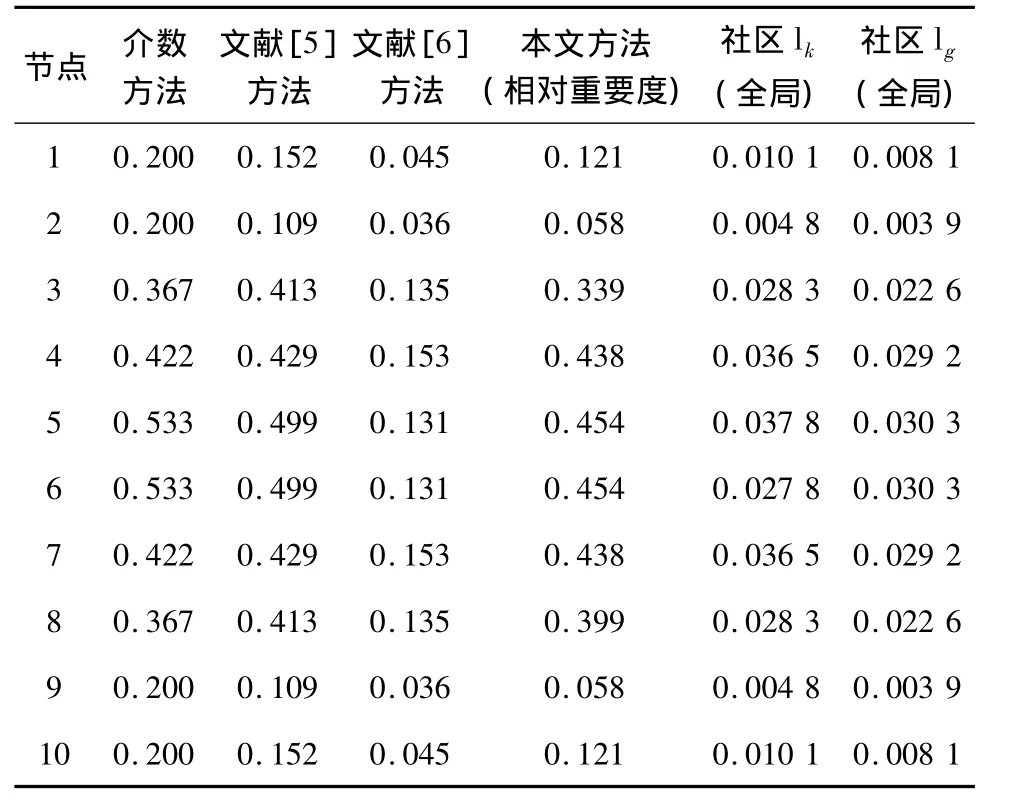
表1 社区l k内节点相对重要度的评估结果、与其他方法计算结果的对比及节点全局重要度评估结果

为了说明节点的全局重要度，本文假设针对一次作战任务存在2个指挥结构、规模相同的社区lk、lg，且分别隶属于A型和B型装备形成的社区功能子集，其中A型社区功能子集中有3个备份，B型社区功能子集中有4个备份，并假设任务M可分解为子任务 M1，M2，M3，子任务重要度都为 1，则任务 M对社区 lk、lg的依赖度分别为 rM→lk=(1/(3+1))(1/(1+1+1))=1/12，rM→lg=1/15，结合节点在社区内的相对重要度，则2个社区节点的全局重要度如表1中社区lk和社区lg两列所示，可以看出:隶属于不同功能子集，但指挥结构相同的社区在应对同一任务时，节点全局重要度出现差异，这一结果与实际作战情况相符，也表明算法是有效的。

4 结论

本文基于无权网络无法深入刻画指挥网络中节点间相互关系细节，不能真实反映网络结构特点的难题，研究了基于加权网络模型的指挥节点重要度评估方法，本文的算法是在静态网络模型下建立的，下一步，将对包括节点增加、删除以及边权随时间变化而变化的动态网络展开进一步研究。

［1］ 贾子英，侯学隆，潘大志．网络化防空体系中作战单元重要度评估［J］．现代防御技术，2013，41(5):12-16．

［2］ 李玉华，贺人贵，钟开，等．动态加权网络中节点重要度评估［J］．计算机科学与探索，2012，6(2):134-144．

［3］ 陈勇，胡爱群，胡啸．通信网中节点重要性的评价方法［J］．通信学报，2005，25(8):129-134．

［4］ 谭跃进，吴俊，邓宏钟．复杂网络中节点重要度评估的节点收缩方法［J］．系统工程理论与实践，2006(11):79-84．

［5］ 朱涛，张水平，郭戎潇，等．改进的加权复杂网络节点重要度评估的收缩方法［J］．系统工程与电子技术，2009，31(8):1902-1905．

［6］ 王甲生，吴晓平，廖巍，等．改进的加权复杂网络节点重要度评估方法［J］．计算机工程，2012，38(10):74-76．

［7］ 张健沛，李弘波．基于拓扑势的网络社区节点重要度排序算法［J］．哈尔滨工程大学学报，2012，33(6):745-753．

［8］ 于会，刘尊，李勇军．基于多属性决策的复杂网络节点重要性综合评价方法［J］．物理学报，2013，62(2):020204-1-020204-9．

［9］ Callaway D S，Newman M E J，Strogatez S H，et al．Network Robustness and Fragility:Percolation on Random Graphs［J］．Physical Review Letters，2000，85(25):5468-5471．

［10］ Budanisky A，Hirst G．Evaluating Word Net-based Measures of Lexical Semantic Relatedness［J］．Computational Linguistics，2006，32(1):13-47．

［11］ Newman M E J．A Measure of Betweenness Centrality Based on Random Walk［J］．Social Networks，2005，27(1):39-45．

［12］ 王欣，姚佩阳，周翔翔，等．指挥信息系统网络节点重要度评估方法［J］．北京邮电大学学报，2011，34(4):38-43．

［13］ 李茂林，龙建国，张德群．基于复杂理论的作战体系节点重要性研究［J］．指挥控制与仿真，2010，32(3):15-19．

［14］ 董涛．基于智能算法的作战任务分解评估研究［D］．西安:空军工程大学，2013．

［15］ 周漩，张凤鸣，李克武，等．利用重要度评价矩阵确定复杂网络关键节点［J］．物理学报，2012，61(5):050201-1-050201-7．

［16］ 赵毅寰，王祖林，郑晶，等．利用重要性贡献矩阵确定通信网络中最重要节点［J］．北京航空航天大学学报，2009，35(9):1076-1081．