基于单元体设计的装甲装备弹目交会建模方法
2014-03-11李光辉范旭东
李光辉,范旭东,陈 晨
(1.装甲兵工程学院装备指挥与管理系,北京100072;2.装甲兵工程学院院务部,北京100072)
武器装备的火力毁伤效果仿真是影响作战仿真可信度的重要因素之一,需要模拟出弹头是否命中、命中部位以及毁伤效果等。装甲装备弹目交会模型主要用于求解作战仿真中火力打击是否命中以及命中部位等问题。目前,作战仿真通常采用蒙特卡罗方法直接产生毁伤效果,可以满足仿真的实时性要求;但此方法没有弹目交会过程以及炮弹命中目标的部位和方向的仿真,无法为进一步确定装备毁伤部件和毁伤等级提供数据基础[1]。另外,计算机图形学中虽有关于线面求交的基本算法[2]134-136,但只能求解线面之间的交点,没有射线和几何体的相交算法,无法直接应用于装甲装备弹目交会仿真中弹头与装备表面的求交问题。
基于此,本文建立了基于单元体的装甲装备弹目交会模型。基于作战仿真产生的装备交火关系,通过该模型可以得到命中部位及相关信息,为装备的毁伤等级分析计算提供基础,提高陆军作战仿真结果的可信度。
1 弹目交会模型
1.1 模型功能需求分析
1)模型输入
弹目交会模型的输入为作战仿真中装备的交火信息,包括弹种、射击参数,攻击装备和目标装备的中心点坐标、方向角、姿态角、炮塔相对车体的角度等。
2)模型输出
模型的输出为目标装备坐标系中的命中点坐标和命中方向。
3)功能适应性
弹目交会模型的适用范围:目标装备包括坦克、装甲战车、自行火炮等;攻击装备主要是坦克和单兵反装甲武器,同时兼顾自行火炮等装备的火力打击;弹药类型主要有穿甲弹、破甲弹,尽管弹药毁伤机理不同,但是在弹头运动轨迹、终点弹道、弹目交会机理等方面是一致的[3]。
1.2 模型结构
弹目交会模型主要包括弹头终点弹道计算模型、基于单元体的装备几何模型、弹头与装备交会计算模型。模型相互关系如图1所示。
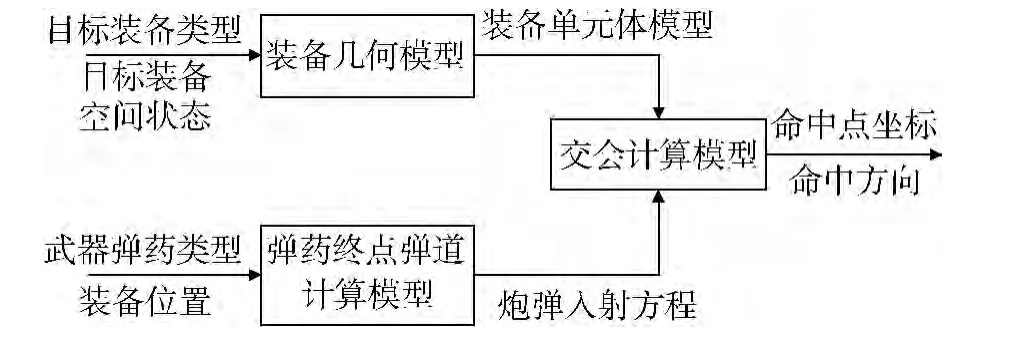
图1 弹目交会模型内部关系
2 基于单元体的装备几何模型
2.1 基本思路
通过装备几何简化原则将目标装备分解为若干个典型几何体,得到几何体的8个端点坐标值,通过端点坐标值确定单元体各表面的方程。通过弹药终点弹道方程与单元体各表面方程遍历求交计算,得到命中部位。由于装备分解为多个单元体,弹头与单元体求交计算量会很大,因此需进行优化分析,采用消隐法可将被遮挡的单元体表面去掉。
2.2 典型单元体的类型
装甲装备的外部构件是多样的,目前三维技术可以较好地模拟外部几何特征,通过长方体、四棱台、三棱锥等基本几何体的组合和排列可以模拟出装甲装备外部构件的基本几何特征。四棱台是最基本的单元体,任意部件都可以简化为由1个或若干个四棱台组成,因此,选取四棱台作为装备几何简化模型的单元体,如图2所示。
2.3 单元体特征的数学描述
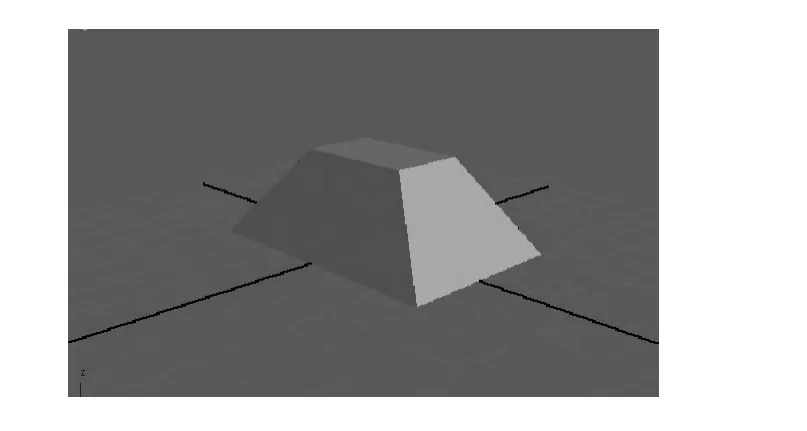
图2 四棱台
装备几何简化模型的建立,主要需要解决的是装备外形的简化,可以借助3Dmax软件完成。在建立3Dmax装备模型时,各基本单元体的端点坐标数据也同时生成。通过单元体8个端点的坐标值,就可以描述单元体以及整个装备的几何模型。在此以四棱台单元体为例,设外表面端点 a,b,c,d,e,f,g,h坐标值分别为 (xa,ya,za),(xb,yb,zb),…,(xh,yh,zh),其中面 abcd,abfe,bcgf,cdhg,adhe,efgh 是外表面,在此以面abfe为例来说明各表面的数学描述。四棱台透视图如图3所示。
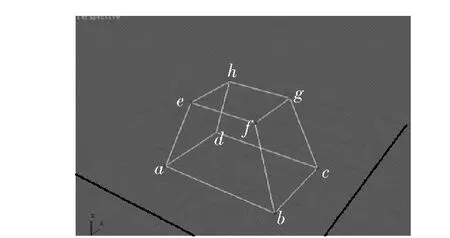
图3 四棱台透视图
面abfe的平面方程表示为[4]
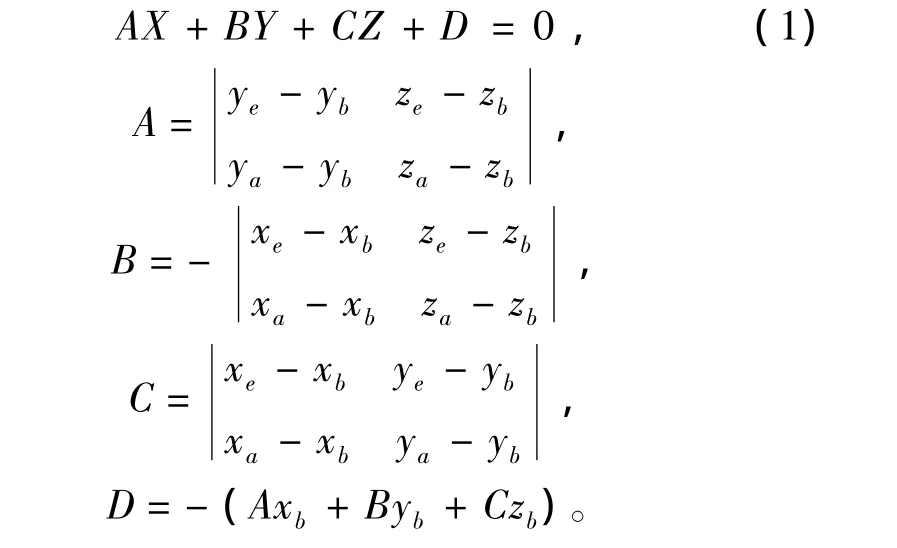
其中端点要按逆时针的方向进行计算,即按b、f、e、a的顺序计算。
2.4 装备模型的简化原则及示例
为了进行求交计算,需对目标装备进行分解简化处理,目标装备外表面方程期望是由多个简单规则的单元体组成。
2.4.1 简化处理的基本原则
1)简化有一定的准确性,考虑到命中点求解的准确性,装备重要部件(如车体、履带、车轮、炮塔、炮管等)的几何外形要与实际基本一致。
2)简化有一定的可行性,要忽略非重要部件,方便计算。
3)对于复杂部件,采取多重简化原则,简单部件可以简化为一个单元体,复杂部件外形复杂多变,需要简化为多个单元体。
4)保持装备外表面的基本形状、倾斜角度、相对位置等重要因素一致。
2.4.2 某型坦克外形模型的分解简化示例
根据简化原则对目标装备外部重点要素(如车体、履带、负重轮、炮塔、炮管等)进行简化。车体、履带由单个四棱台描述,炮管由单个长方体描述,负重轮由6个四棱台组成,炮塔由3个四棱台组成。坦克外形模型简化结果如图4所示。

图4 某型坦克简化模型
3 弹目交会建模
3.1 相关坐标系说明
弹目交会模型涉及到3种坐标系,即:攻击装备坐标系,以攻击装备几何中心点为坐标系原点,以装备纵轴向前为x轴正方向;大地坐标系,为作战仿真系统坐标系;目标装备坐标系,与攻击装备坐标系定义相同。本文坐标系转换应用布尔萨七参数法。
作战仿真系统产生的装备位置信息(即装备中心点坐标、俯仰角α、侧滚角β、方向角γ)需要转换为由装备中心点和4个装备端点组成的坐标,转换公式为

式中:x、y、z为四端点的实际坐标值;x'、y'、z'为姿态角为0°情况下的四端点坐标值。
中心点坐标用于描述装备的具体位置状态,4个端点坐标用于描述装备具体姿态状态。采用这种方法是为了满足弹目交会仿真中准确性的需求。坐标系转换公式为
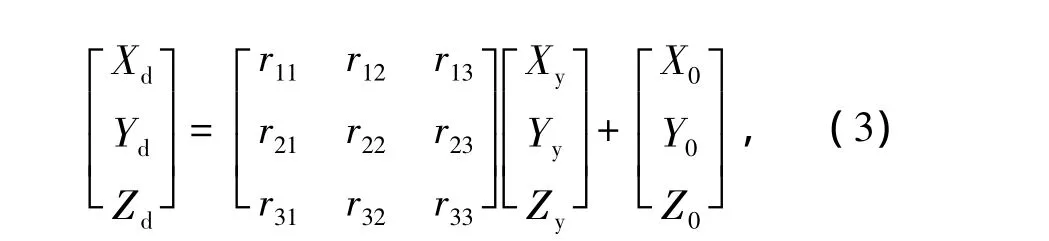
式中:Xy、Yy、Zy为已知坐标系中的坐标值;Xd、Yd、Zd为待求坐标系中的坐标值;rij(i,j=1,2,3)为旋转参数 εx、εy、εz的三角函数[5]。
对于炮塔,其坐标系在目标装备坐标系基础上,根据炮塔旋转角进行转换即可得到。
3.2 弹头终点弹道计算模型
计算弹头终点弹道方程需要求得目标截面交点位置坐标、弹道方向向量。由于地面火炮武器系统弹药会受到武器自身以及外界环境因素的影响,因此命中点与瞄准点出现误差是不可避免的。根据射击误差理论可知:每次射击的误差都是由诸元误差和散布误差2部分综合组成,诸元误差是确定的,散布误差符合正态分布[6]。本文采用蒙特卡罗方法计算得到射击误差,用(X1,Y1,Z1)、(XZ,YZ,ZZ)、(XS,YS,ZS)分别表示射击误差(射击精度)、诸元误差(射击准确度)、散布误差(射击密集度),则有
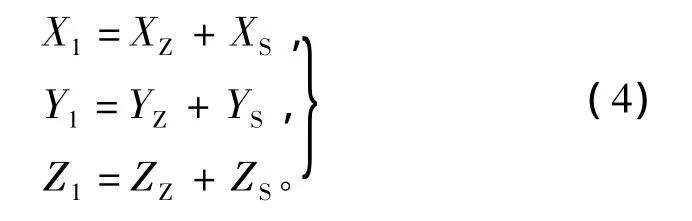
通过射击误差可以得到弹药与目标截面交点位置坐标为 (x1,y1,z1)。
根据作战仿真系统产生的装备位置信息(作战仿真系统给出的位置信息是在大地坐标系内的坐标值,需要通过式(3)转换为攻击装备坐标系中的坐标值),计算弹头终点射线方向角和弹头落角,图5、6分别是在XOY平面和YOZ平面的弹头终点弹道。
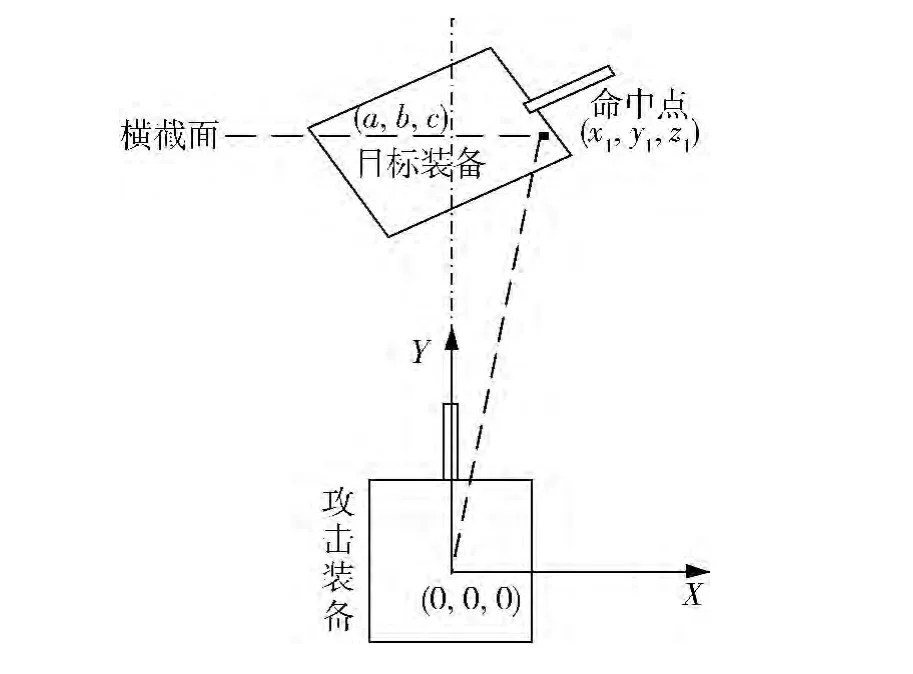
图5 XOY平面弹头终点弹道
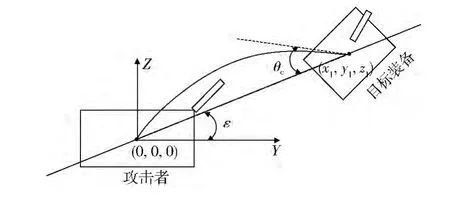
图6 YOZ平面弹头终点弹道
根据解析几何直线方程定义,已知直线上一点和直线方向向量,可以确定该直线方程。因此,求得弹头与目标截面交点位置坐标(x1,y1,z1)后,只需求得方向向量,就可以确定弹头终点弹道方程。设弹头终点弹道方程方向向量为(m,n,p),目标装备位置坐标(中心点)为 (a,b,c),θc为落角,ε 为弹目高度角。方向向量与目标截面交点、落角、弹目高度角近似关系为[7]
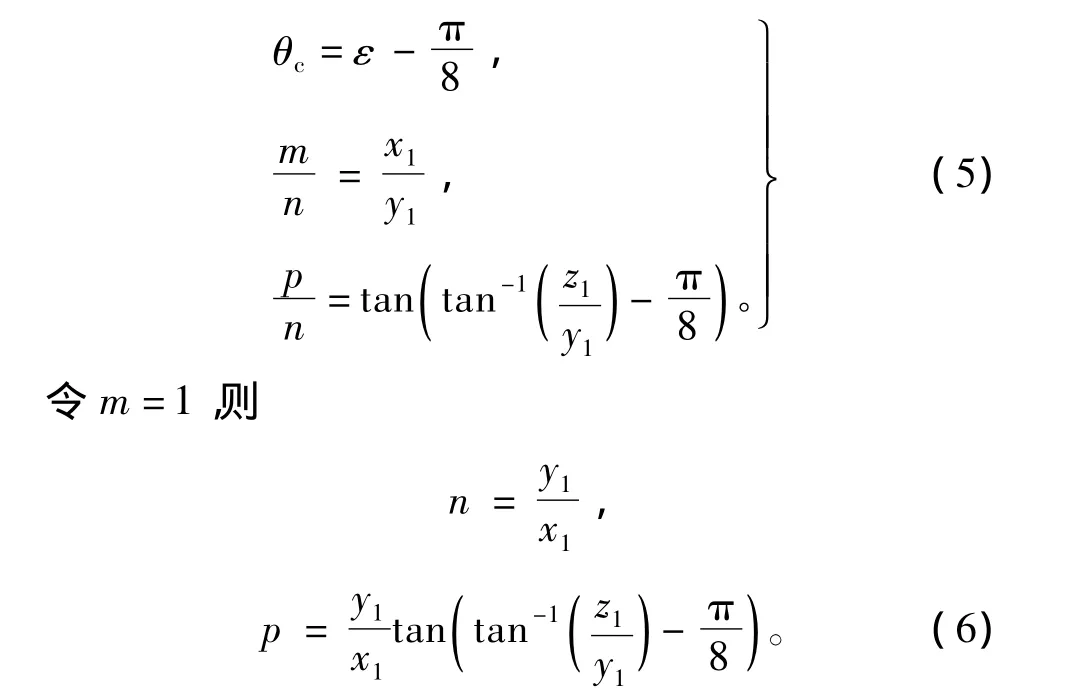
得到弹头终点弹道方程:
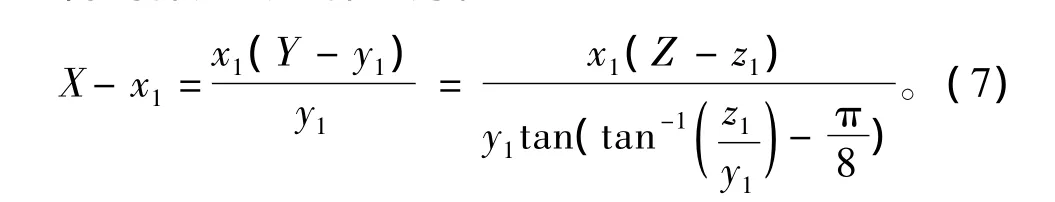
3.3 弹头与目标交会模型
3.3.1 四棱台求交会计算
以图3所示的面abfe为例,说明弹头与四棱台的求交算法。通过式(1)可以得到面abfe的方程。弹头终点弹道方程由式(7)得到,并通过式(3)将2个方程转换为目标装备坐标系下方程。命中点坐标可以通过求解弹头终点弹道和单元体外表面方程组得到:
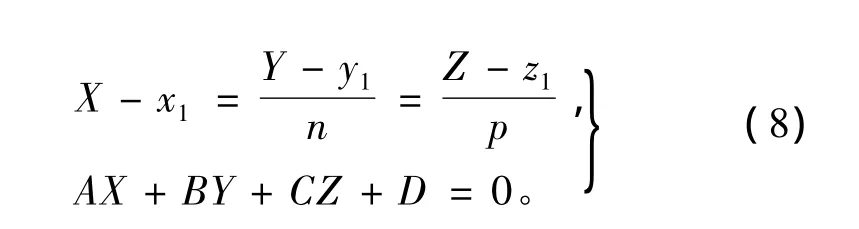
通过解方程组(8)得到命中点坐标:
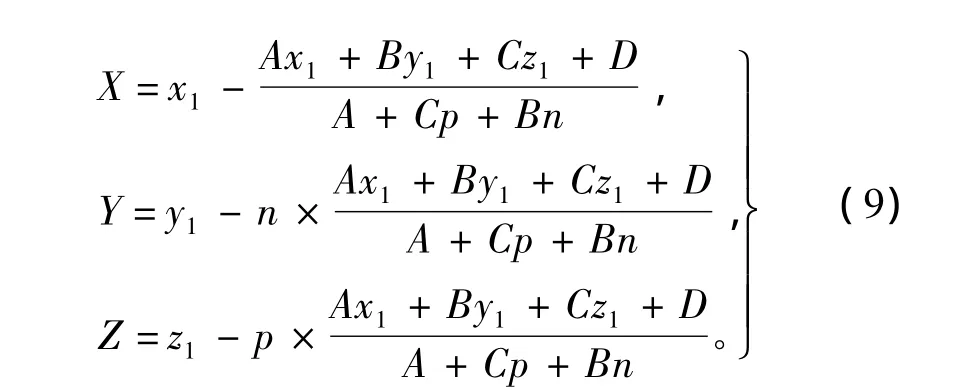
由式(9)得到的命中点位置还需要进一步判断是否在面abfe内,如果超出表面界限,则视为未击中。可利用叉积判断法判断命中位置是否在表面内。设命中位置为p0,面abfe的4个端点为p1、p2、p3、p4,vi=pi-p0,i=1,2,3,4,当所有叉积 vi× vi+1的符号都相同时,则判断此命中位置在面abfe内;反之,则判断为未命中。其他各表面同理可得。
通过遍历6个表面与弹头终点弹道交会计算,可能会得到2个命中点坐标,这是由弹头先后与2个表面交会造成的,必须选择首先交会的命中点作为实际命中位置。通过比较2个命中点与攻击者中心的距离,距离较短的即为实际命中点。
3.3.2 多单元体的计算优化
目标装备经过简化分解,一般都是由若干个单元体组合而成,所以需要考虑在多单元体的情况下如何计算与弹头终点弹道的交点位置问题。如果继续按照遍历的方法进行计算,对组成装备的所有单元体进行求交计算,计算量将会非常大,因此需采用消隐矢量法简化计算。以某炮塔模型为例,从任意角度射击该炮塔模型,总会有某些表面被前面的表面所遮挡,不会被击中,因此为了方便计算,应当将其省略。可根据2个矢量来确定物体表面的可见性:第1个矢量是面的法向量(A,B,C);第2个矢量是射线方向矢量 (1,n,p)。因此可得2个矢量夹角的余弦值[2]204-206:

当cosθ>0,即A+Bn+Cp>0时,则为可见的面;当cosθ<0,即A+Bn+Cp<0时,则为不可见的面,应忽略。可见面的求交计算和单元体计算步骤相同。
4 实例验证
以某型坦克为例,按照弹目交会基本流程进行弹目交会计算。
4.1 弹目交会基本流程
仿真系统产生火力打击事件后,弹药终点弹道计算模型根据初始条件,利用已知的攻击武器弹药散布,通过随机数产生平面弹头命中点,利用平面命中点坐标、落角、弹目高度角,最终确定弹头终点弹道方程。装备几何模型根据简化原则,将目标装备简化分解为多个规则的单元体,并且产生各端点坐标值和各装甲面方程。弹头弹道与装备交会计算模型利用弹头终点弹道方程和装备单元体各面方程的交会分析与计算,最终得到弹目交会命中部位坐标。基本流程如图7所示。
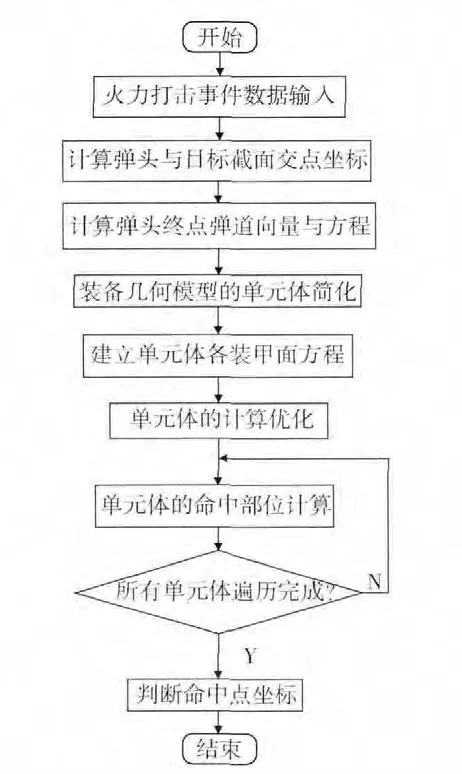
图7 弹目交会基本流程
4.2 模型的实时性测试
采用Microsoft Visual Studio 2010软件,对弹目交会模型进行编程,计算机硬件条件:CPU为Intel奔腾处理器,3.0 GHz,1 GB内存,无独立显卡。程序运行1 000次,运行时间为3.05 s。程序运行1 000次,相当于作战仿真系统中营级单位的作战计算量,计算效率较高,但准确性要高很多。与图形求交软件相比,其更具有实用性和针对性。
4.3 模型正确性验证
此火力打击事件发生后,将作战仿真系统产生的数据作为模型条件:攻击者中心位置坐标为(-250,143,3.2);目标装备中心位置坐标为(0,141,2.2);姿态角 α =0.1 rad,β =0.1 rad,γ =0.1 rad;目标炮塔旋转角为0.1 rad。通过随机数产生弹头与目标截面交点位置的大地坐标系坐标为(0,249,3)。通过计算得到弹头终点弹道射线方程方向向量为(1,-0.008,-0.000 5)。
由装备简化分解得到装备的单元体,通过弹头终点弹道射线方程与单元体的交会计算,得到弹目交会点在目标装备中心坐标系的坐标为(-24,0.77,2.48),打击命中点位于左侧履带装甲板,所得结果与实际打击试验所得结果基本一致。
5 结论
通过建立基于单元体设计的装甲装备弹目交会模型,可以较为准确地计算出弹目交会点坐标,该模型能够满足作战仿真系统实时性与准确性的要求,以及作战仿真系统火力打击效果仿真的需求。该模型具备较好的适应性,可拓展应用于火炮、反坦克类武器的火力打击模拟。
模型基于单元体的解决思路对于弹目交会分析计算来说是可行的,实际应用于作战仿真系统中可以进一步进行打击概率仿真实验,为毁伤仿真研究提供数据基础。
[1] 吕跃广,方胜良.作战实验[M].北京:国防工业出版社,2007:12-13.
[2] 孙家广.计算机图形学[M].3版.北京:清华大学出版社,2006.
[3] 刘向刚,李雄,付佳.陆军装备发展概论[M].北京:国防大学出版社,2011:67-68.
[4] 谢冬秀.解析几何[M].北京:科学出版社,2009:45-46.
[5] 孙艳崇.不同基准下坐标转换的方法及注意事项[J].价值工程,2014(11):241-242.
[6] 路航,石全,胡起伟,等.基于蒙特卡罗法的弹着点散布仿真[J].计算机与数字工程,2011,39(7):15-16.
[7] 胡梦中,衣同胜,潘佳梁,等.基于射表数据的火炮弹道仿真分析方法[J].无线电工程,2013,43(12):41-44.
