工程陶瓷单晶压痕边缘破碎理论研究与机理分析

田欣利，王 龙，王望龙，吴志远，唐修检

(装甲兵工程学院装备再制造技术国防科技重点试验室，北京100072)

一般工程陶瓷磨削加工时，磨粒与工件形成赫兹应力区，导致陶瓷工件在弹塑变形边界的最大拉应力处产生微裂纹，主要产生2类裂纹系统:中位/径向裂纹和侧向裂纹［1-2］。由于在工程陶瓷加工过程中，边缘自由表面附近的应力场有较少的约束，降低了中位裂纹和侧向裂纹系统在陶瓷内部扩展的阻力，使得裂纹易于朝着边缘方向迅速扩展并穿透边缘表面，形成不

规则的“豁口”状边缘破碎现象［3-5］。边缘破碎的生成涉及裂纹的生成、扩展，与材料的力学性能参数(弹性模量、断裂韧性等)和加工条件等有重要关系。

边缘破

碎损伤一直被视为陶瓷加工质量控制研究的重点关注现象［6］。本文通过单晶压痕边缘破碎实验研究和线弹性断裂力学数值仿真分析，对边缘破碎产生机理以及主要影响因素进行研究，为控制边缘破碎和提高加工质量提供借鉴。

1 单晶压痕边缘破碎实验

1．1 实验条件

实验系统如图1所示。采用微机控制电子万能试验机，利用金刚石压头对反应烧结氮化硅陶瓷试件进行加载施压，直至陶瓷边缘发生脆性断裂，从显示屏上读取整个过程的载荷随位移变化。

反应烧结氮化硅陶瓷材料性能参数为:弹性模量 160 GPa，断裂韧性 2．85 MPa/m1/2，泊松比 0．26，抗拉伸强度120 MPa。

图1 单晶压痕边缘破碎实验系统

1．2 实验结果与分析

在加载速度为50 mm/min时，金刚石压头距陶瓷边缘不同距离情况下，压头加载力与压头位移之间的变化关系如图2所示。显然不同于金属材料，它会随着加载压力的数值变大到一峰值后突然发生脆性断裂。图3为陶瓷材料脆性断裂力值P与压头距边缘距离H的变化关系，可见P/H呈现一定的正相关性，其主要取决于自身的断裂韧性等材料性能。

图2 压头加载力-压头位移变化曲线

图4为断裂力值与压头加载速度的变化关系，可见:随着加载速度的增大，发生边缘破碎时的断裂力值逐渐变小。

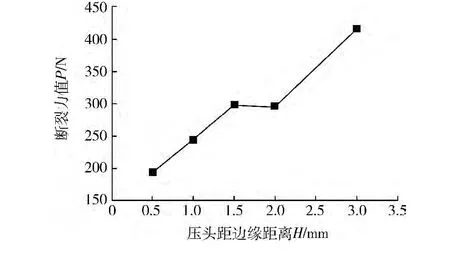
图3 断裂力值-压头距边缘距离的变化关系

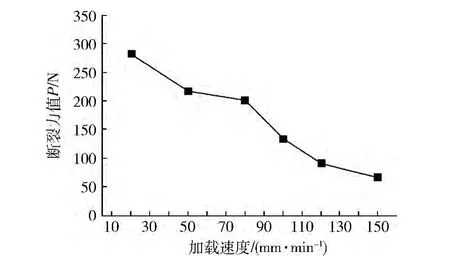
图4 断裂力值-压头加载速度的变化关系

图5 不同压头加载速度的加载力-压头位移变化关系

图5为金刚石压头距陶瓷边缘为1 mm，压头加载速度分别为20 mm/min和120 mm/min时，加载力随位移的变化关系。由图5(b)可知:当压头加载速度提高到一定程度时，产生的直接动载冲击作用力较大，使得陶瓷更容易发生边缘脆性破碎;此外，随着加载速度的增大，陶瓷发生边缘破碎的峰值作用力变小。

由于陶瓷材料内部会随机分布一些微裂纹和微孔隙，在外加载荷作用下，这些微缺陷会发生扩展、演化，在局部形成微贯通，甚至形成宏观裂纹，发生边缘破碎。陶瓷脆性材料在冲击载荷作用下，可用损伤力学来动态地描述陶瓷内部微裂纹的损伤演化规律。TCK模型［7］推导的损伤演化方程为

式中:D为损伤变量;ν为连续均匀的泊松比;¯ν为含裂隙的泊松比。

当D=0时，可认为陶瓷无损伤;当0＜D＜1时，其为陶瓷损伤累积过程;当D=1时，陶瓷发生脆性断裂。

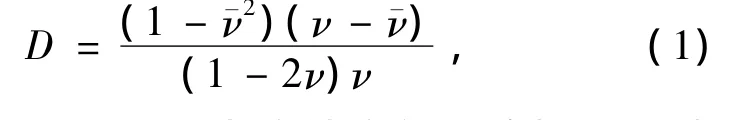
2 单晶压痕应力场数值分析

单晶压头轴向挤压时陶瓷工件材料内任一微元体处的应力状态如图6所示。于爱兵等［8］根据弹性

图6 应力场示意图

理论推导出单金刚石颗粒磨削作用下的应力状态分析公式为

式中:Fn为作用力;R、θ、φ为应力场位置参数。

由于边缘破碎单晶压头模型是轴向挤压，此时φ=0，则式(2)可简化为主应力空间公式，即

由式(3)可以看出:边缘破碎单压头挤压应力场的某点应力状态的主要影响因素为R和Fn。图7为施加压力Fn=150 N时平面各处的应力σrr的分布情况，可见:其压痕处的应力很大，四周的应力迅速变小。

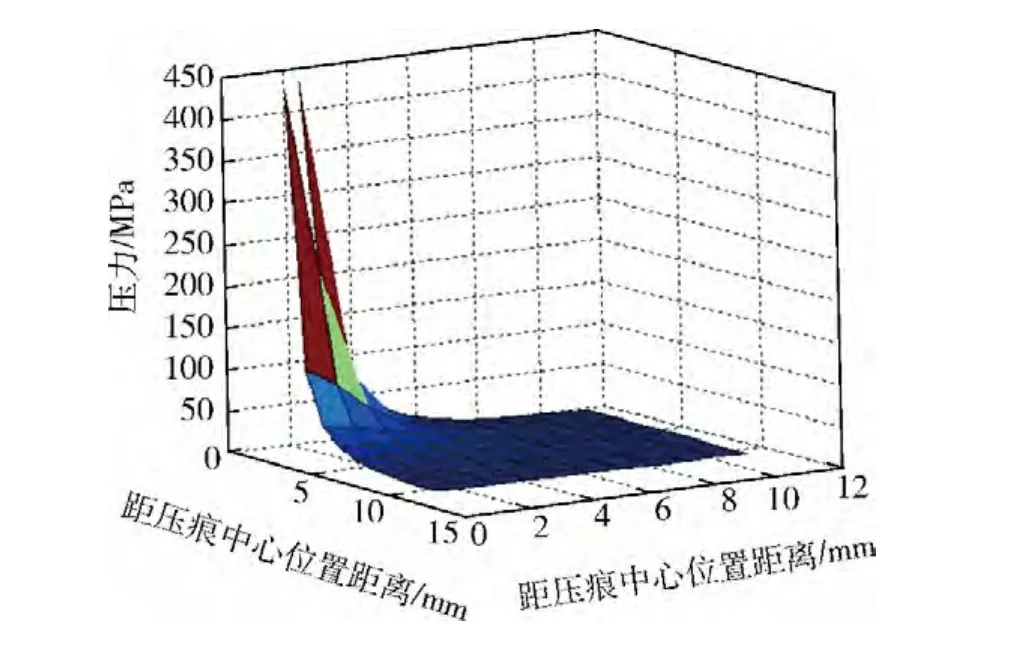
图7 压痕处横截面内应力σrr分布情况

采用ansys有限元分析三维Si3N4陶瓷受静态压载荷时的应力场分布情况如图8所示。当压痕位置距边缘距离D=0，2，4 mm时，分别得到最大拉应力值为395，178，100 MPa，如图9所示。可见:压痕位置对氮化硅陶瓷发生边缘破碎影响较大，随着压痕位置离边缘越远，最大拉应力越小，使得Si3N4陶瓷发生脆性断裂需要的外界挤压应力值越大，其仿真结果与前面断裂力值随压头离边缘距离变化实验结论一致。

采用 ansys有限元分析Si3N4陶瓷受到D=0 mm，F=300 N的应力场，以压痕位置为原点沿三轴方向的变化情况如图10所示，显然仿真结果与应力场分布模型计算结果的变化趋势一致。

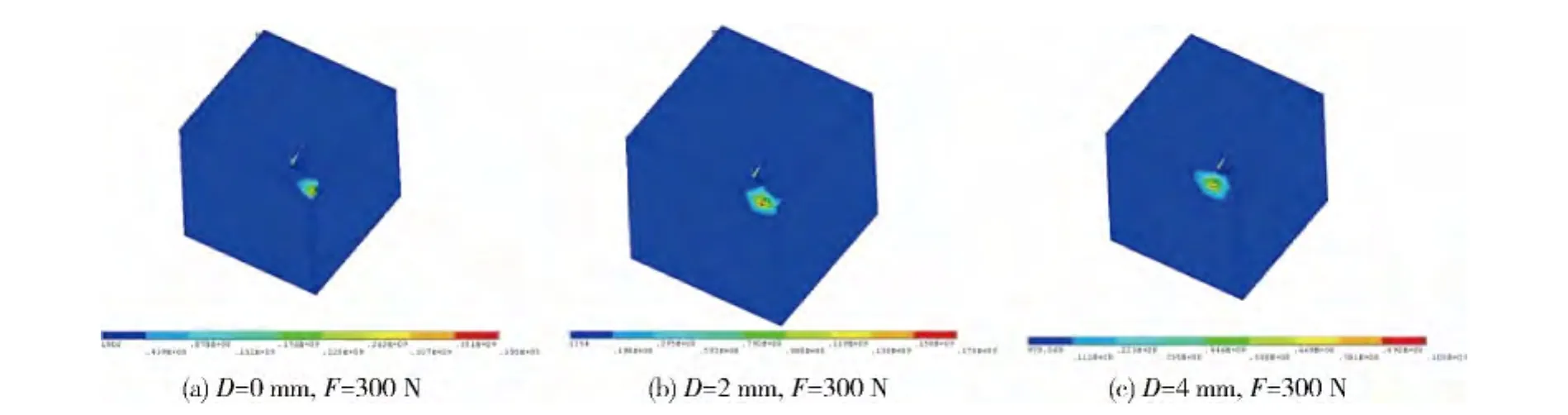
图8 不同条件下的应力场分布

图9 最大拉应力-压痕距边缘距离的关系曲线

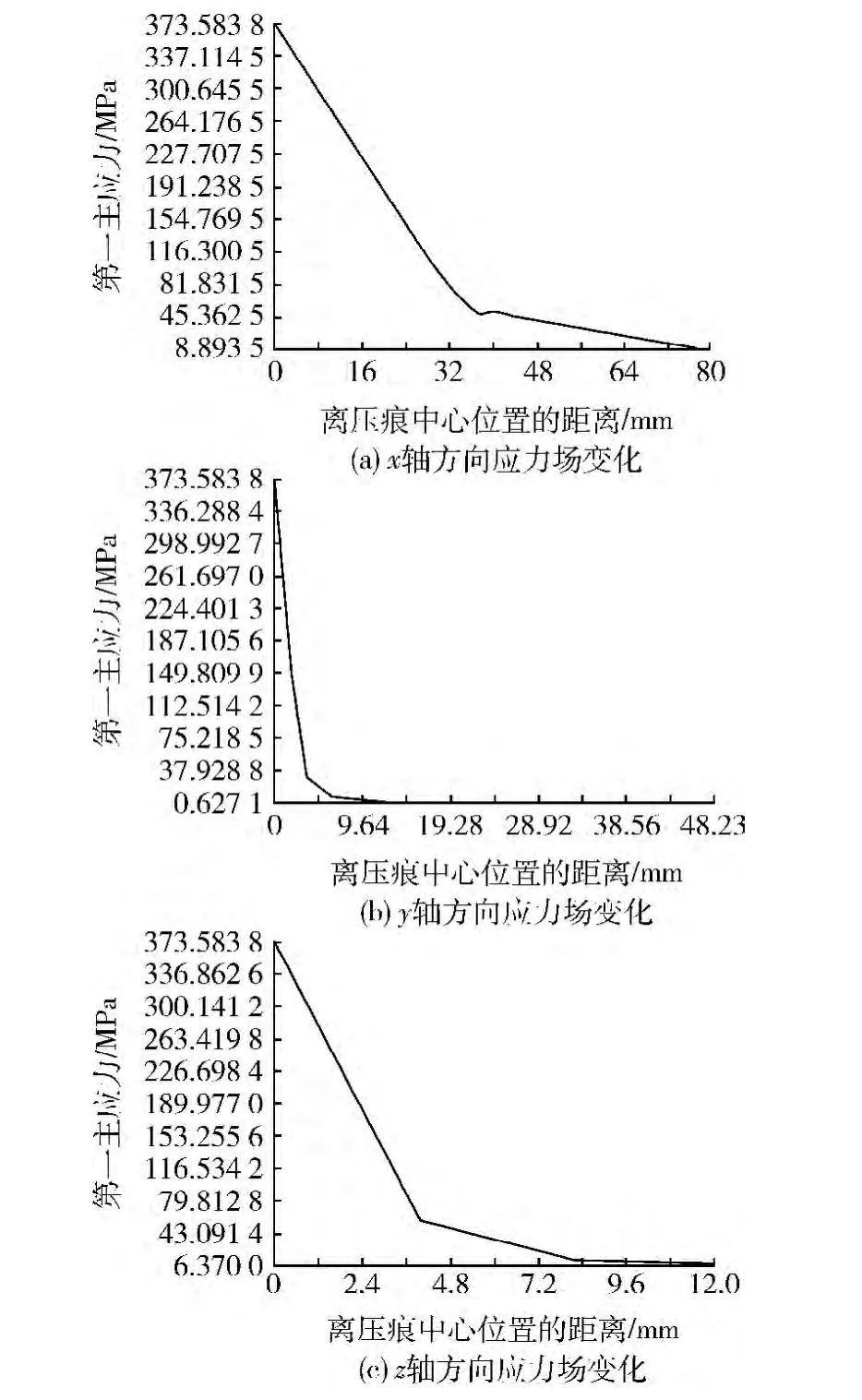
图10 应力场沿三轴方向应力变化

3 边缘破碎的生成机理

图11为单晶压痕边缘破碎实验后压痕部位形貌，显然在压头与陶瓷材料的弹/塑接触部位形成裂纹源，产生中位/径向裂纹和侧向裂纹，压痕裂纹的成核及生长都符合压痕断裂力学模型分析陶瓷材料去除机理的结论。中位裂纹向下深处扩展时偏向自由表面，侧向裂纹向两侧扩展，总体去除材料部位呈1/4椭圆状。由于其裂纹尖端塑性区尺寸远小于裂纹长度，可根据线弹性断裂力学理论研究工程陶瓷的脆性破裂［9］。

图11 单晶压痕边缘破碎实验后压痕部位形貌

压痕断裂力学模型的裂纹成核机制理论包括中位裂纹成核机制和位错塞积模型［1］，都验证存在使压痕裂纹生成的临界载荷Pc，

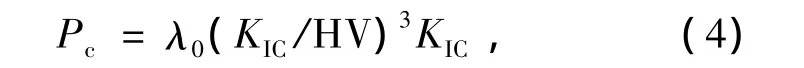
式中:λ0为无量纲常数;KIC为材料断裂韧度;HV为材料维氏硬度。

图12为扫描电镜观察到的反应烧结Si3N4陶瓷的边缘破碎部位微观形貌，可以看出:宏观边缘碎裂和材料崩碎缺陷底部含有大量微观裂纹和裂纹不规则扩展形成的微观破碎。裂纹按扩展方式可分为张开型裂纹、滑移型裂纹和撕开型裂纹，工程陶瓷应用中最常见低应力断裂的主因是张开型裂纹［10］。这些裂纹尖端和破碎边缘尖锐处的应力集中使得缺陷成为潜在的断裂源，在外力冲击作用下，即使外力低于理论断裂载荷，也可能发生裂纹失稳扩展和贯通，形成块状或片状的断屑，造成边缘破碎。

图12 陶瓷边缘破碎底部微观形貌

Chiu等［11］将裂纹尺寸、应力加载和材料断裂韧性3个因素建立联系，当应力强度因子KI超过材料断裂韧性KC时就会发生边缘破碎，应力强度因子KI为

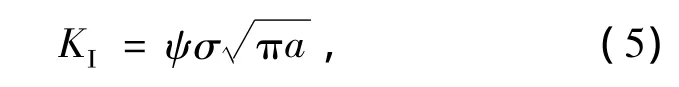
式中:ψ为试件形状或裂纹位置等综合影响因子;σ为加载应力;a为裂纹尺寸。

4 结论

1)单晶压痕边缘破碎实验结果表明:陶瓷材料发生边缘脆性断裂时，断裂力值P与压头距边缘位置H呈现一定的正相关，与压力加载速度呈现负相关;当加载速度较缓慢时，陶瓷在发生破碎前会有一个线弹性渐变过程，然而当加载速度增大到一定数值时，陶瓷材料会受冲击而直接失稳断裂。

2)通过单晶压痕应力场数值分析和仿真，阐述了材料受到外加压应力作用下的应力场分布情况和破碎条件，以及压痕距边缘位置对应力场的影响，其结论与实验结果一致。

3)压痕部位形貌验证了压痕断裂力学模型对边缘破碎机理研究具有一定的适用性。通过边缘破碎缺口显微形貌观察，发现存在微观裂纹和微观破碎，边缘破碎是缘于裂纹失稳扩展和贯通。

［1］ 于思远．工程陶瓷材料的加工技术及其应用［M］．北京:机械工业出版社，2008．

［2］ 田欣利，于爱兵．工程陶瓷加工的理论与技术［M］．北京:国防工业出版社，2006．

［3］ Scieszka SF．Edge Failure as a Means of Concurrently Estimating the Abrasion and Edge Fracture Resistance of Hard-metals［J］．Tribology International，2005，38(9):834-842．

［4］ Morrell R，Gant A J．Edge Chipping of Hard Materials［J］．International Journal of Refractory Metals＆ Hard Materials，2001，19(4/6):293-301．

［5］ 唐修检，田欣利，王望龙，等．基于能量的工程陶瓷边缘碎裂损伤规律与机理研究［J］．人工晶体，2013，42(10):1-4．

［6］ 唐修检，田欣利，吴志远，等．工程陶瓷边缘碎裂行为与机理研究进展［J］．中国机械工程，2010，21(1):114-119．

［7］ Taylor L M．Microcack-induced Damage Accumulation in Brittle Rock under Dynamic Loading［J］．Computer Methods in Appl Mech ＆ Eng，1986，55:301-320．

［8］ 于爱兵，田欣利，韩建华，等．应用压痕断裂力学分析陶瓷材料的磨削加工［J］．硅酸盐通报，2002，21(1):58-61．

［9］ 李庆芬，胡胜海，朱世范．断裂力学及其工程应用［M］．哈尔滨:哈尔滨工程大学出版社，2006．

［10］ 赵建生．断裂力学及断裂物理［M］．武汉:华中科技大学出版社，2003．

［11］ Chiu W C，Thouless M D，Endres W J．An Analysis of Chipping in Brittle Materials［J］．International Journal of Fracture，1998，90(4):287-298．