两个有序分类变量构建一个分类复合终点指标方法的模拟评价*

郭正梅阎小妍姚 晨，△

两个有序分类变量构建一个分类复合终点指标方法的模拟评价*

郭正梅1阎小妍2姚 晨1，2△

目的对于临床试验有效性评价中两个或可以转变为两个均为有序分类变量的主要终点指标，提出一种最乐观或最悲观的构建分类复合终点的方法，分析这种方法的合理性及应用性。方法采用MonteCarlo模拟的方法，考虑调整样本量和相关系数，分析分类复合终点指标进行疗效评价的Ⅰ型错误和检验效能，并与多重检验和连续复合终点指标的结果进行比较。结果Ⅰ型错误方面，随着样本量和相关系数的增大，两个主要终点指标均有统计学意义的多重检验的Ⅰ型错误远低于检验水准0.05，至少一个主要终点指标有统计学意义的多重检验的Ⅰ型错误在0.04至0.05之间，分类复合终点指标和连续复合终点指标的Ⅰ型错误均保持在0.05左右。检验效能方面，整体上，分类复合终点指标的检验效能、连续复合终点的检验效能和至少一个主要终点指标有统计学意义的多重检验的检验效能接近，三者均大于两个主要终点指标均要有统计学意义的多重检验的检验效能，后者最保守。各方法的检验效能与两个主要终点指标间相关系数的关系因赋值不同而有不一样的变化趋势。结论对于临床试验两个或可以转变为两个均为有序分类变量的主要终点指标的资料，可根据临床实际意义构建最乐观或最悲观分类复合终点指标，其能得出可解释的综合水平，能控制Ⅰ型错误且具有较高的检验效能。而且无论相关系数大小，都可以构建分类的复合终点指标，因为乐观与悲观之间没有固定的优劣关系，使得研究者在实际研究过程中根据实际情况来构建评价指标，而不是倾向于选择乐观的方法来构建，避免这一倾向带来的偏倚。

多个主要终点指标有序分类变量Ⅰ型错误检验效能

临床有效性指标根据研究目的通常被分为主要指标（primary endpoint）和次要指标（secondary endpoint），主要指标的选择通常是能反映临床试验的主要目的，同时易于量化、客观性强、可重复性高并在相关研究领域已有公认的准则或标准的临床有效性评价指标。但是，这一情形在一些疾病或者临床试验中并不适用，例如，病因未明的疾病，由于缺乏一个最重要的临床公认评价指标以多角度呈现自身的疾病，以及治疗领域现行的评价疗效的方法决定从多方面来选择疗效指标并对疗效指标进行评价的疾病。这样，就会出现多个终点指标（multiple endpoints），当采用多个主要终点指标进行多重检验时就会存在检验的多重性问题，就需要在方案设计时制定出有效的策略和方法来事先控制I类错误率（family-w ise error rate，FWER），常用的控制I类错误的方法有Bonferoni方法、Holm方法、Shaffer方法等［1］，为了达到预期的检验效能，所需要的样本量就会增大；当进行两个干预方案比较时，由于多个主要终点指标对病人健康的重要性不同，而且每个指标比较时不同方案之间的优劣差异也是不一致的，此时就很难判断孰优孰劣；若多个主要终点指标均为中间终点（intermediate endpoint），与病人最终疗效评价之间的关系存在不确定性［2］。

解决以上问题的方法之一是构建一个能够综合反映多个主要终点的复合终点（composite endpoints）。目前，有关疾病治疗方面应用复合终点的研究仍然是临床试验设计与分析关注的领域，存在的争议也很多［3］。尽管使用复合终点具有诸多优势：首先，它可以提高终点事件的发生率，从而减少所需的样本量，这应是研究者选择复合终点最主要的原因。其次，使用复合终点可以有效的避免竞争风险。再次，当选择几个重要性相似的终点指标存在争议时，应用复合终点既可以避免这一选择上的困惑，还能更全面的评价干预措施的疗效，提高统计学检验效能，因为一个终点指标往往只能反映干预措施有效性和安全性的某一方面。但Neaton等认为对同等重要的终点指标选择有困难时不能作为使用复合终点的理由［4］。使用复合终点也存在诸多局限性：第一，使用复合终点最常见的缺陷是当治疗措施对各个终点指标的影响不一致时，复合终点会削弱统计学检验效能，可能对结果解释产生误导，最极端的情况是干预措施对构成指标的疗效截然相反。第二，当各终点事件对患者重要性不一致时，对结果的解释可能存在困难，而且制定复合终点也比较复杂，需要计算各指标的权重。第三，使用复合终点需要准确的确定其组成事件，而且即使复合终点疗效评价指标被认为具有统计学意义和临床相关性，也应同时报告干预措施对各组成事件的影响，才能据此得出可靠的结论，此时需要根据实际情况调整I类错误率［5-7］。

为了准确和可靠地评估研究药物的有效性和安全性，理想情况下，主要终点指标应该尽量是数值型连续变量。然而，在实践中，有时患者对治疗的反应根据一些有意义且定义明确的事件发生情况去记录，如死亡、感染、某种疾病治愈和任何严重不良事件，且这些事件的强度能被一些事先定义好的类别进行分级，所以分类数据在一些未观察到潜在的连续变量的临床试验中是有用的替代终点。有时候，为了便于分析或更好地呈现有临床意义的结果，甚至将连续数据根据一些预先定义的标准转化为分类数据。因此，在临床试验中，许多疗效和安全性终点是以名义分类或有序分类数据的形式记录的［8］。继而出现了使用多个均为有序分类变量的主要终点指标来构建复合终点评价指标的临床试验，所构建的复合终点评价指标包括基于变量权重构建的连续复合终点和基于临床实际意义构建的分类复合终点，笔者对这部分内容已经发表了一篇文章［9］，本文旨在对构建分类复合终点方法的合理性和应用性进行模拟评价。

就如何构建分类复合终点，在此我们只考虑最乐观综合评价和最悲观综合评价两种方法，本文以两个有序五分类的主要疗效指标为例来说明主要方法的定义，假设分类1到分类5表示疗效从好到差，表1表示两个主要疗效指标复合时，综合平价按照疗效更好的评价，即最乐观综合评价；表2则表示主要疗效指标复合时，综合平价按照疗效更差的评价，即最悲观综合评价。

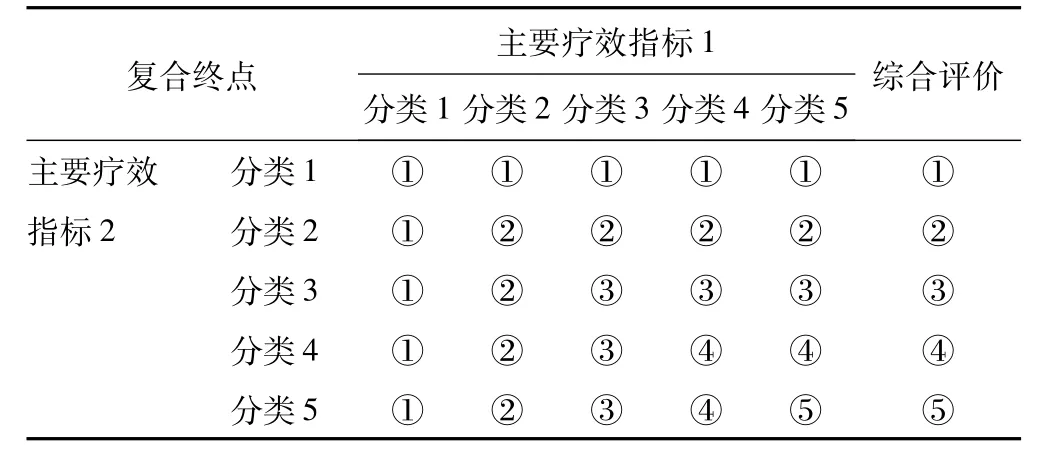
表1 最乐观综合评价

表2 最悲观综合评价

就如何构建连续复合终点，下面就以SF-36量表中“躯体疼痛”这一个维度为例进行说明，其由两个项目组成，其中疼痛强度分6类、疼痛干扰工作分5类，传统的SF-36评价方法如下表3，其实质是首先对两个项目各分类赋分，根据实际情况给每个项目一个权重（此处权重为1），然后将各项目得分乘以其权重相加得出的和为连续复合终点的值［10］。

模拟研究方法

由于本文是针对临床试验两个或可以转为两个均为有序分类变量的主要终点指标，所以本研究的多重检验和分类复合终点的组间比较均采用秩和检验，连续复合终点的组间比较，当数据满足正态性时采用t检验，当不满足时采用秩和检验。数据模拟由计算机完成，模拟数据的软件采用SASversion 9.2（SAS Institute Inc.），进行t检验的SAS过程为PROC TTEST过程，进行秩和检验的SAS过程为PROC NPAR1WAY过程。

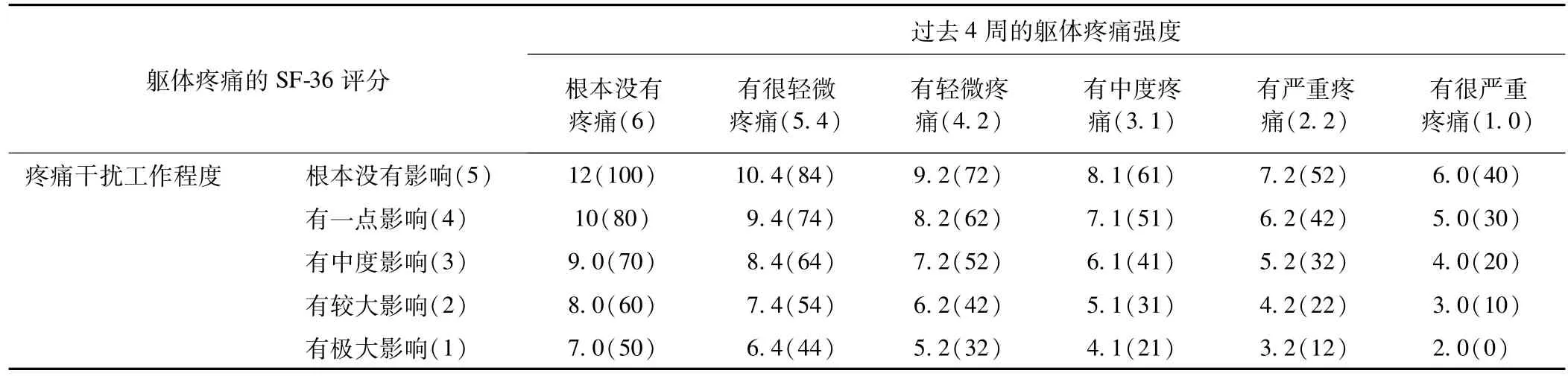
表3 传统的SF-36评价方法

本研究设定的模拟次数为10000次，模拟比较了终点间相关系数为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、0.95（不考虑相关系数为1的情况是因为：如果两个主要终点指标完全相关，就没有必要两个都作为主要终点指标），以及两组样本量均为50，100，150，200，250这50种模拟情形下几种方法的Ⅰ型错误和检验效能。构建连续复合终点时，两主要疗效指标的各类别赋分均假设为3、2、1、0、-1，并计算各种模拟情形下权重比为0.4·0.6、0.5·0.5、0.6·0.4（因为当两指标重要程度相当时，才会都作为主要终点指标）时连续复合终点的Ⅰ型错误和检验效能。共模拟比较以下几种分析方法：

①最乐观综合评价，检验水准均为0.05；

②最悲观综合评价，检验水准均为0.05；

③多重检验，两个主要终点指标均要有统计学意义，单个主要终点指标的检验水准为0.05；

④多重检验，至少一个主要终点指标要有统计学意义，单个主要终点指标的检验水准为0.025；

⑤连续复合终点评价指标，权重比为0.4：0.6、0.5：0.5、0.6：0.4，检验水准均为0.05。

为了验证上面所提出的方法的合理性，以两个组别、两个有序分类的疗效指标为例进行比较说明，这里给出了Monte Carlo模拟的思路、过程及结果，以供读者参考。

模拟过程及结果

1.分类复合终点、多重检验和连续复合终点Ⅰ型错误的模拟比较

（1）模拟数据集的产生和参数设置

Ⅰ型错误又叫假阳性，即拒绝了实际上成立的H0。因此，比较Ⅰ型错误时，模拟比较的两个样本应来自同一个总体。如上所述，以两个治疗组别、两个有序五分类的主要疗效指标为例来进行模拟比较，其中相应组别的各主要疗效指标的各分类的背景率假设如下：

A组主要疗效指标1的各分类背景率假设为0.001、0.015、0.231、0.708和0.045，五个率之和为1；

A组主要疗效指标2的各分类背景率假设为0.030、0.106、0.197、0.606和0.061，五个率之和为1；

B组主要疗效指标1的各分类背景率假设为0.001、0.015、0.231、0.708和0.045，五个率之和为1；

对模拟产生的数据集进行模拟研究方法所述各种情形的几种方法检验分析，计算所有模拟检验中出现阳性结果（P≤α）的比率即该检验方法的Ⅰ型错误水平。

（2）模拟结果

模拟结果表明随着样本量的增大，各种方法的Ⅰ型错误无明显变化，所以只给出样本量为50时的Ⅰ型错误图形，从图1可以看出，随着相关系数的增大（此处横坐标的相关系数为模拟产生的A、B组数据的两组两主要终点指标间相关系数的平均值），两个主要终点指标均要有统计学意义的多重检验的Ⅰ型错误越来越大，但是远低于0.05；至少一个主要终点指标要有统计学意义的多重检验的Ⅰ型错误有下降趋势，但是都在0.04至0.05之间；分类复合终点评价指标和连续复合终点评价指标的Ⅰ型错误均保持在0.05左右。

图1 不同相关系数时各种方法的Ⅰ型错误（n＝50）

2.分类复合终点、多重检验和连续复合终点检验效能的模拟比较

（1）模拟数据集的产生和参数设置

检验效能（1-β）又叫把握度，即当两总体确有差异时，按规定检验水准（α）所能发现该差异的能力。在检验效能的模拟比较中，分析用数据集应来自两个确有差别的总体。如上所述，以两个治疗组别、两个有序五分类的主要疗效指标为例来分别进行比较说明，根据某一实际的临床试验结果，各组各分类的背景率假设如下：

1.3.1 对照组 对照组给予乳腺外科常规围手术期干预，包括完善术前相关检查，进行相关知识及手术流程宣教，术后预防感染等。

A组主要疗效指标1的各分类背景率假设为0.001、0.015、0.231、0.708和0.045，五个率之和为1；

A组主要疗效指标2的各分类背景率假设为0.030、0.106、0.197、0.606和0.061，五个率之和为1；

B组主要疗效指标1的各分类背景率假设为0.033、0.083、0.283、0.600和0.001，五个率之和为1；

B组主要疗效指标2的各分类背景率假设为0.033、0.217、0.333、0.400和0.017，五个率之和为1。

模拟情形参见模拟研究方法部分，对模拟数据集进行各种情形的几种方法检验分析，计算所有模拟检验中出现阳性结果（P≤α）的比率即为该方法的检验效能。

（2）模拟结果

由图2-4可以看出，随着样本量的增大，检验效能越来越大，当样本量为200时，各方法的检验效能已经几乎重叠且接近100%了，当样本量为250时，重叠的趋势更加明显，所以样本量为200和250的图形省略。整体上，分类复合终点评价指标的检验效能接近连续复合终点和至少一个主要终点指标均要有统计学意义的多重检验的检验效能；两个主要终点指标均要有统计学意义的多重检验最保守，除了两个主要终点指标均要有统计学意义的多重检验的检验效能随着相关系数的增大有增大趋势外，其他方法的检验效能均有随着相关系数的增大有减小的趋势。

图2 不同相关系数时各种方法的检验效能（n＝50）

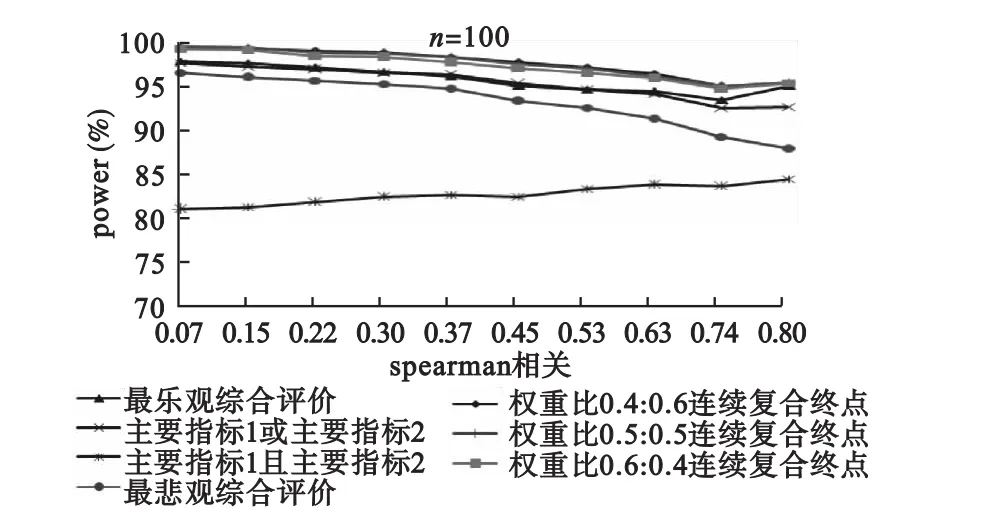
图3 不同相关系数时各种方法的检验效能（n＝100）

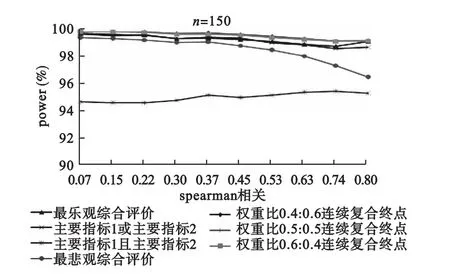
图4 不同相关系数时各种方法的检验效能（n＝150）

但是，当假设的背景率不同时，不能得出乐观与悲观方法谁大谁小，也不能得出随相关系数有增高或减小的固定趋势，但是根据所有模拟结果能得出，整体上，分类复合终点评价指标的检验效能、连续复合终点的检验效能和至少一个主要终点指标要有统计学意义的多重检验的检验效能接近，三者均大于两个主要终点指标均要有统计学意义的多重检验的检验效能，后者最保守。

讨论与结论

Ⅰ型错误和检验效能是反映一种检验方法合理与否的两个重要指标，笔者考察了对于临床试验两个或可以转变为两个均为有序分类变量的主要终点指标，模拟比较了分类复合终点指标、多重检验和连续复合终点指标的Ⅰ型错误和检验效能。模拟结果说明，随着样本量和终点间相关系数的增大，无论是连续复合终点还是分类复合终点，其Ⅰ型错误均在检验水准0.05左右，这纠正了一些研究者认为构建复合变量会增大Ⅰ型错误的认识，说明了这种方法不会增加将无效的药物推向市场而给病人的健康和生命带来威胁；至少一个主要终点指标要有统计学意义的多重检验的Ⅰ型错误有下降趋势，但是都在0.04至0.05之间，两个主要终点指标均要有统计学意义的多重检验的Ⅰ型错误越来越大，但是远低于0.05。检验功效方面，随着样本量的增大，检验效能越来越大，在样本量为50时，分类复合终点指标的检验效能和连续复合终点的检验效能已有70%左右，而两个主要终点指标均要有统计学意义的多重检验的检验效能只有50%左右，本模拟结果进一步验证，为了达到预期的检验效能，使用复合终点可以减少所需的样本量；当假设的背景率不同时，虽然检验功效虽然没有固定的变化趋势，但是整体上，分类复合终点指标的检验效能、连续复合终点的检验效能和至少一个主要终点指标要有统计学意义的多重检验的检验效能接近，三者均大于两个主要终点指标均要有统计学意义的多重检验的检验效能，后者最保守，结合Ⅰ型错误和检验效能的模拟结果，可见前三种方法更可取。

但是，目前国内关于多个主要终点问题的讨论和方法虽多，但多停留于学术上的研究，真正应用到实际中的并不多见，尤其是考虑到终点间相关性的文献甚少，尚无较成熟的方法。而实际情况是多终点问题常常被忽视，从而直接影响了试验结果的可信度。研究表明，在使用多重检验的临床试验中校正多终点检验时，终点间的相关性不容忽视［11］。既往关于多个主要终点的研究有的没有明确提出对总I类错误率控制的问题，有的研究即使控制了总I类错误率，往往也没有考虑到多个主要疗效评价指标之间的相关性；近年来出现了一些考虑到终点间相关性的控制总I类错误率的方法，如James＇P值校正法［12］，属不多的考虑到终点间相关性的校正方法之一，其原理是基于标准多元正态分布对各个终点检验的Pi值进行校正，检验水准不变，该方法优点是将终点间相关系数引入校正公式，充分考虑到了终点间的相关性，在多终点间高度相关时能较好地控制试验总的Ⅰ类错误［13］。缺点是要求终点间等相关，不等相关时近似估计等相关系数，且公式复杂实际应用中难以推广。

再者，构建连续复合终点时，将多个主要终点各类别赋分再加权得总分的研究的科学性有待商榷，因为，其一，如何给各终点的各类别赋分？有一个共同的观点认为有序分类变量的测量性能是有序的，而不是一个具体的数值，不论标签的类型，有序数据只包含顺序信息，而不是大小或距离信息。有序变量是可按序排列的多分类变量，纽约心脏病协会的心功能分级就是一个例子，将心功能分为四个等级，尽管这四级是有序排列的，但是1级（体力活动不受限制）和2级（体力活动轻度受限）之间不存在数量上的差别，而1级和2级之间的差别也不等同于3级（体力活动明显受限）和4级（不能从事任何体力活动，休息时亦有症状）之间的差别。再如，没有任何理由认为个人反应表示的替代方式，如“一点也不”（1），“轻微”（2），“中等”（3），“相当”（4）和“极度”（5）服从相等的间隔。统计方法必须不受任何形式标签的影响，这意味着代数的基本操作没有可能被应用到有序数据，并且从数据的数学计算得出的结论可能是无效的。不幸的是，尽管有这方面的知识，在实践中，研究者常常将间隔测量水平视为定量数据。其二，各个终点的权重如何确定？尤其是当各个终点间存在相关性时，各个终点的权重就更难确定。目前，虽然存在一些确定变量权重的方法，但是由于这些方法自身尚存在的一些缺陷，因此在该问题上业界意见还不一致。其三，我们通过构建连续复合变量的方法得出的数值，只有大小信息，没有实际的临床意义，而构建分类复合终点的方法考虑到数据的非计量性质，较容易理解和使用，所以该方法可以提供一个可解释的综合水平，如表3中阴影部分表示分类复合后的一个分类（如为⑤），如果一组病人的躯体疼痛的中位数恰好为⑤，它意味着这组病人的躯体疼痛平均水平为＂（无）很轻微疼痛，不干扰工作＂，而这组病人相应的SF得分的平均数，却只能提供数值大小的信息，没有实际的临床意义。

因为不同设定数值时，不能得出乐观与悲观方法谁大谁小，也不能得出随相关系数有增高或减小的固定趋势，但是根据模拟结果能得出，在控制Ⅰ型错误的前提下，分类复合终点指标的检验效能、连续复合终点的检验效能和至少一个主要终点指标要有统计学意义的多重检验的检验效能接近，三者均大于两个主要终点指标均要有统计学意义的多重检验的检验效能，其最保守。这个结果说明无论相关系数大小，都可以构建分类的复合终点评价指标，而且乐观与悲观之间没有固定的优劣关系，使得研究者在实际研究过程中根据实际情况来构建评价指标，而不是倾向于选择乐观的方法来构建，避免这一倾向带来的偏倚。此外，进一步验证多个主要终点指标比较时，合理控制Ⅰ型错误的重要性，理论上，检验水准一致时，至少一个主要终点指标有统计学意义的多重检验，其检验效能必然在一定程度上大于两个主要终点指标均要有统计学意义的多重检验；而减小至少一个主要终点指标有统计学意义的多重检验的检验水准，会降低其检验效能，如本文至少一个主要终点指标要有统计学意义的多重检验，此时单个主要终点指标的检验水准减小为0.025，结果这种多重检验的检验效能仍远大于两个主要终点指标均要有统计学意义的多重检验的检验效能，说明检验水准降低后至少一个主要终点指标有统计学意义的多重检验的检验效能依然高于两个主要终点指标均要有统计学意义的多重检验。

在此值得一提的是，关于多个主要终点指标均要有统计学意义的多重检验的检验水准问题，如果研究允许的总Ⅰ类错误率是双侧0.05，则每个主要指标的检验水准都定为双侧0.05。本文两个主要终点指标均要有统计学意义的多重检验最保守的结论与Offen W和Chuang-Stein C等［14-15］的观点一致，他们也认为这种方法降低了研究的检验效能，并提出了平均I类错误方法，基于合理的假设，该方法提高了单个终点的检验水准，关于平均I类错误方法不是本文重点，所以不做过多讨论，读者可以参考相关文献。

所以，虽然临床试验分类复合终点的使用应在没有其它更好的办法时才使用，但是当临床试验的主要终点指标不止一个、指标间存在相关性且各主要终点指标的重要性程度不同时，却不失为一个好的选择。对于临床试验两个或可以转变为两个均为有序分类变量的主要终点指标的资料，可采用根据临床实际意义构建分类复合终点评价指标分析方法，该方法可以提供一个可解释的综合水平，能控制Ⅰ型错误且具有较高的检验效能。我们希望通过本研究能够帮助促进大家对复合终点的理解，将复合终点相关问题明朗化，期望同行的后续深入研究和探讨。

1.王彤，易东.临床试验中多重性问题的统计学考虑.中国卫生统计，2012，29（03）：445-450.

2.李洪超，张银花，刘国恩，等.糖尿病治疗终点指标综述与复合终点的权重构建.中国药物经济学，2010，（2）：42-53.

3.Ferreira-González I，Permanyer-M iralda G，Busse JW，et al.Methodologic discussions for using and interpreting composite endpoints are lim ited，but still identify major concerns.Journal of Clinical Epidem iology，2007，60（7）：65l-657.

4.Neaton JD，Gray G，Zuckerman BD，et al.Key issues in endpoint selection for heart failure trials：composite endpoints.JCard Fail，2005，11（8）：567-575.

5.彭菊聪，孙甜甜，李伦，等.复合终点.中国循证儿科杂志，2012，07（4）：305-307.

6.Rauch G，Kieser M.An expected power approach for the assessment of composite endpoints and their components.Computational Statistics and Data Analysis，2013，60：111-122.

7.Rauch G，Kieser M.Multiplicity adjustment for composite binary endpoints.Methods Inf Med，2012，51（4）：309-317.

8.Chow SC，Liu JP.Design and analysis of clinical trials：concepts and methodologies.New York：W iley-Interscience，2003：339-340.

9.郭正梅，姚晨，阎小妍.临床试验复合终点评价指标的构建方法概述.中国新药杂志，2013，22（23）：62-69.

10.Svensson E.Construction of a single global scale formulti-item assessments of the same variable.StatMed，2001，20（24）：3831-3846.

11.王陵，蒋志伟，李婵娟，等.多终点变量对药物疗效评价的影响.中国新药杂志，2011，20（24）：2396-2408.

12.James S.Approximate multinormal probabilities applied to correlated multiple endpoints in clinical trials.Stat Med，1991，10（7）：1123-1135.

13.Leon AC，Heo M.A comparison ofmultiplicity adjustment strategies for correlated binary endpoints.JBiopharmStatis，2005，15（5）：839-855.

14.Offen W，Chuang-Stein C，Dm itrienkoA，etal.Multiple co-primary endpoints：medical and statistical solutions.Drug Inf J，2007，41（1）：31-46.

15.Chuang-Stein C，Stryszak P，Dm itrienko A，et al.Challenge ofmultiple co-primary endpoints：new approach.StatMed，2007，26（6）：1181-1192.

（责任编辑：刘 壮）

Simulation Evaluation of Constructing a Categorical Com posite Endpoint from Two Ordered Categorical Variables

Guo Zhengmei，Yan Xiaoyan，Yao Chen（Peking University First Hospital，Peking University（100034），Beijing）

ObjectiveFor two or can be converted to two ordered categorical primary endpoints of clinical trials，proposethemostoptim istic or pessim isticmethod to construct categorical composite endpointand evaluate reasonableness and applicability of thismethod.MethodsThrough Monte Carlo simulation，consider adjusting the sample size and correlation coefficient，compare typeⅠerror and power of efficacy evaluation among threemethods（categorical composite endpoint index，multiple testing and continuous composite endpoint index）.ResultsIn terms of typeⅠerror，w ith the increase of sample size and correlation coefficient，typeⅠerror of multiple testing that two primary endpoints are statistically significant is far below 0.05，and multiple testing that at leastone primary endpoint is statistically significant is between 0.04 and 0.05，while typeⅠerror of categorical composite endpointand continuous composite endpoint indexes aremaintained around 0.05.In terms of power，power of categorical composite endpoint，power of continuous composite endpoint and power of multiple testing that atleast one primary endpoint is statistically significantare close.The former thre epowers aremuch larger than power ofmultiple testing that two primary endpoints are statistically significant，which is themost conservative.But there is different trend of power change for different correlation coefficients between the two primary endpoints.ConclusionFor two or can be converted to two ordered categorical primary endpoints of clinical trials，we can constructthemostoptimistic or pessimistic categorical composite endpointaccording to actual clinicalmeaning，which can provide useful interpretable comprehensive level and increase power under the control of typeⅠerror.And whatever the size of the correlation coefficient，we can build categorical composite endpoint，because there is no fixed relationship about the pros and cons between optim istic and pessim istic methods.So in real clinical trials，researchers w ill construct categorical composite endpoint index according to the actual situation，rather than tending to choose optim istic approach and avoiding the tendency to bring bias.

Multiple primary endpoints；Ordered categorical variables；TypeⅠerror；Power

*：建设国际标准数据管理和统计分析平台（2012ZX09303019-001）

1.北京大学第一医院（100034）

2.北京大学临床研究所

△通讯作者：姚晨，E-mail：13801378685＠139.com