两组计量资料非劣效检验的P-P曲线评价方法*

哈尔滨医科大学卫生统计学教研室（150086） 侯 艳 李 康

两组计量资料非劣效检验的P-P曲线评价方法*

哈尔滨医科大学卫生统计学教研室（150086） 侯 艳 李 康△

目的针对两组计量资料的非劣效性评价问题，给出一种新的统计检验方法。方法根据计量资料的不同评价分界值，给出相应的试验组和对照组的“有效率”，分别以两组的“有效率”为横轴和纵轴，连成P-P曲线并计算曲线下面积，然后根据这一统计量进行统计检验，并通过模拟实验对检验效能进行研究。结果给出了P-P曲线方法的检验公式，使用这种方法更易于选择非劣效界值，而且对数据的分布没有任何限制，在偏态情况下比传统方法有更高的检验效能。结论该方法适合用于Ⅱ期探索性临床试验研究，具有应用和研究价值。

临床试验非劣性试验非劣效界值P-P曲线

在新药临床试验中，经常需要比较试验药物是否非劣于阳性对照药物的疗效，例如新的治疗方法与标准治疗相比安全性方面可能更有优势，其疗效只要在允许的非劣效界值范围内即可。两组计量资料的非劣效性评价，一般采用两组均数的差值进行衡量和检验。非劣效界值的确定是设计的关键，通常需要根据阳性对照的效应、具体疾病特征、临床意义等进行确定［1-2］。传统的检验方法需要假定数据服从正态分布，如果数据明显呈偏态，分析的结果则可能不正确，而且选择的非劣效界值也可能失去意义。本文提出P-P曲线这一新的概念和方法，阐述了它与传统临床试验非劣效评价方法的关系，在此基础上推荐了新的非劣效检验的界值标准，这种方法对数据的分布没有任何限制，而且在偏态分布时同样能够保证其检验效能。

原理与方法

1.P-P曲线及曲线下面积

假定标准组和试验组的疗效变量Y服从任意分布，G表示分组变量，G＝0表示标准组，G＝1表示试验组，各自服从方差为σ2（G）的分布，同时假定测量值越大疗效越好（高优指标）。对于定量终点评价指标，试验组和标准组的分布通常有较大的重叠，如果将其分为“有效”和“无效”两类，选择不同的阈值会得到不同的结果（图1）。现用横坐标πT（c）和πS（c）分别表示试验组和标准组的“有效率”，不断改变“有效率”的阈值c，获得一条连续的曲线，对此称之为P-P曲线，并用参数θ表示曲线下面积（0≤θ≤1）。从图2可以看到，如果试验组与标准组的疗效完全相同，P-P曲线是由（0，0）到（1，1）的45°角的直线，直线下面积为θ＝1/2；当试验组的疗效不如标准组时，曲线下面积θ＜1/2；当试验组疗效优于对照组时，曲线下面积θ＞1/2。记Δθ＝1/2-θ表示两组疗效的平均差别，Δθ愈大说明试验组的疗效与对照组相差愈大，当Δθ＜0时，说明试验组的疗效优于标准组。

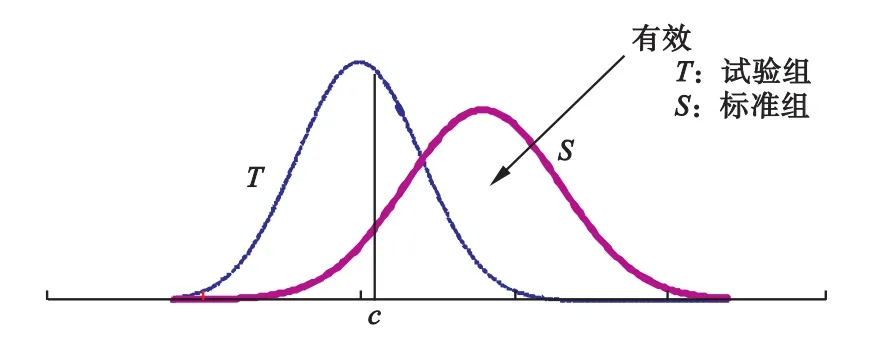
图1 试验组与标准组疗效测量结果的概率分布与确定有效率的阈值

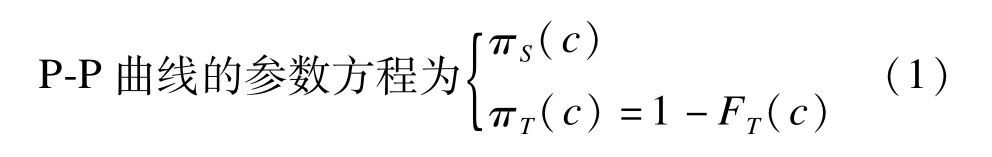
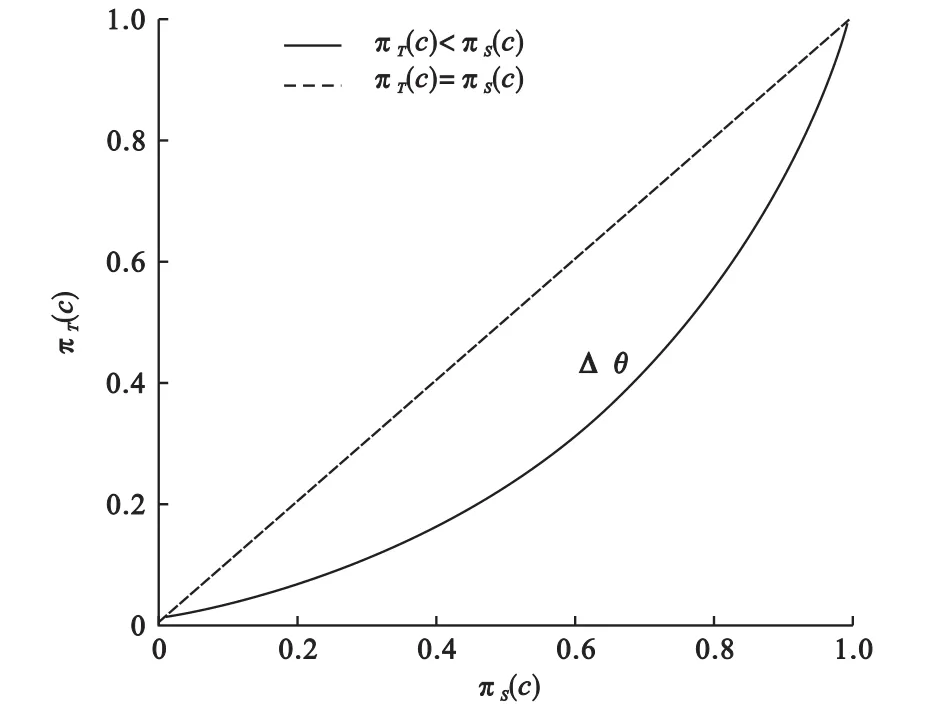
图2 试验组和标准组的P-P曲线示意图

FT（c）和FS（c）分别是试验组和标准组的分布函数，PP曲线方程可以表示为

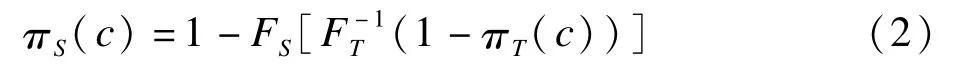
特殊地，当标准组和试验组的疗效分别服从N的正态分布时，容易推出P-P曲线方程：

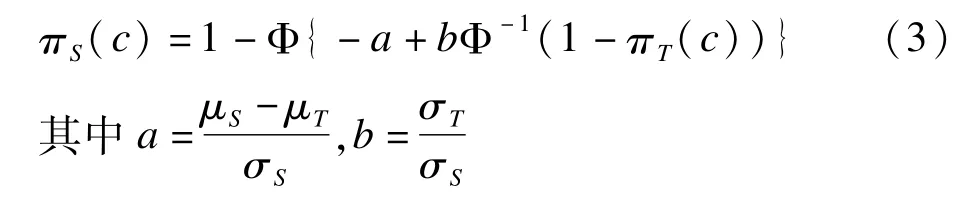
Φ（·）为标准正态的分布函数。P-P曲线下的面积为

2.Δθ值的意义

下面我们证明两组有效率差值与P-P曲线下面积θ之间的关系［3］。

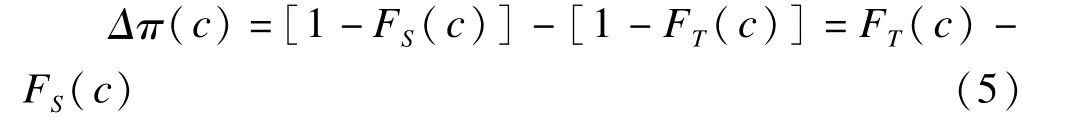
两总体率的最大差值max｛Δπ（c）｝的截断点c*可以通过解下面方程得到，即

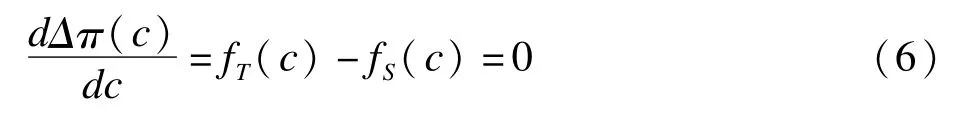
其中fS（c）和fT（c）分别为标准组和试验组测量结果的密度函数。容易证明，c*恰为两密度曲线的相交点，同时是P-P曲线上45°切线上的点。在正态分布假定下，有

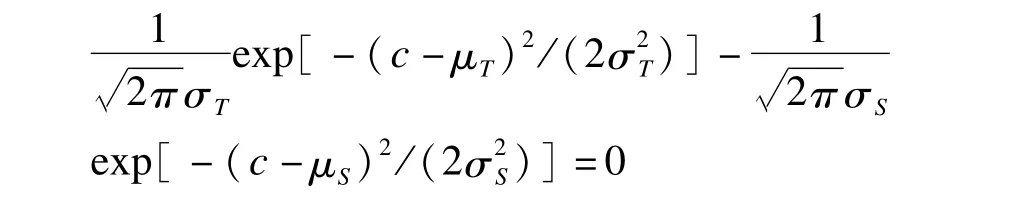
c*的解由下式决定：

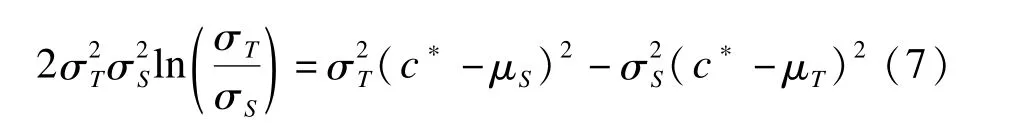
两总体率的最大差值：

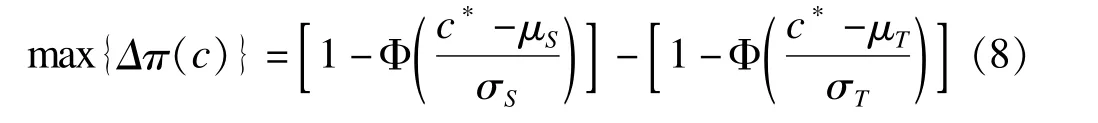
特殊地，在σT＝σS时，c*＝（μS＋μT）/2，于是P-P曲线下面积的参数θ与max｛Δπ（c）｝之间的数量关系为

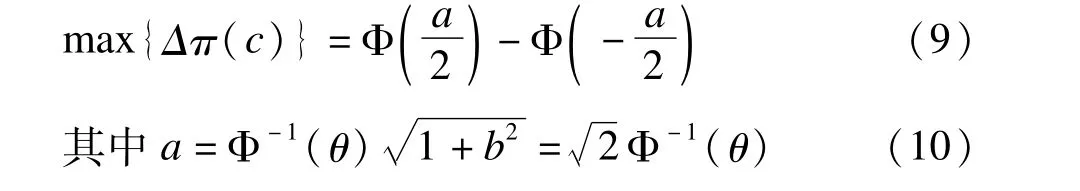
max｛Δπ（c）｝与Δθ的具体数量关系见表1。例如Δθ＝0.05，max｛Δπ｝＝0.0708，表示在双正态同方差假定下，无论怎样选择“有效率”的阈值c，标准组与试验组的有效率之差最大不超过7.08%。RR表示对应c值的两组有效率的比值。实际上，在非正态情况下（如Weibull分布），只要方差相同，max｛Δπ（c）｝与Δθ的关系与正态分布的情况相差不大（如max｛Δπ（c）｝＜0.08）。为便于应用，表1和表2给出了标准组在各百分位点时不同指标的对应值。例如，标准组的有效率为0.80，在选择Δθ＝0.05作为非劣效界值时，相当于取两组有效率的最大差值max｛Δπ（c）｝＝0.0534为界值。为便于比较，同时也给出了相应的两组有效率的比值RR。可以看出，选择Δθ＝0.05是一个较为适当的选择，此时max｛Δπ（c）｝＝0.0534，在πS＞0.40的情况下，能够保证max｛RR（c）｝≤1.20，作为非劣效的界值基本上能够满足目前临床试验的要求。

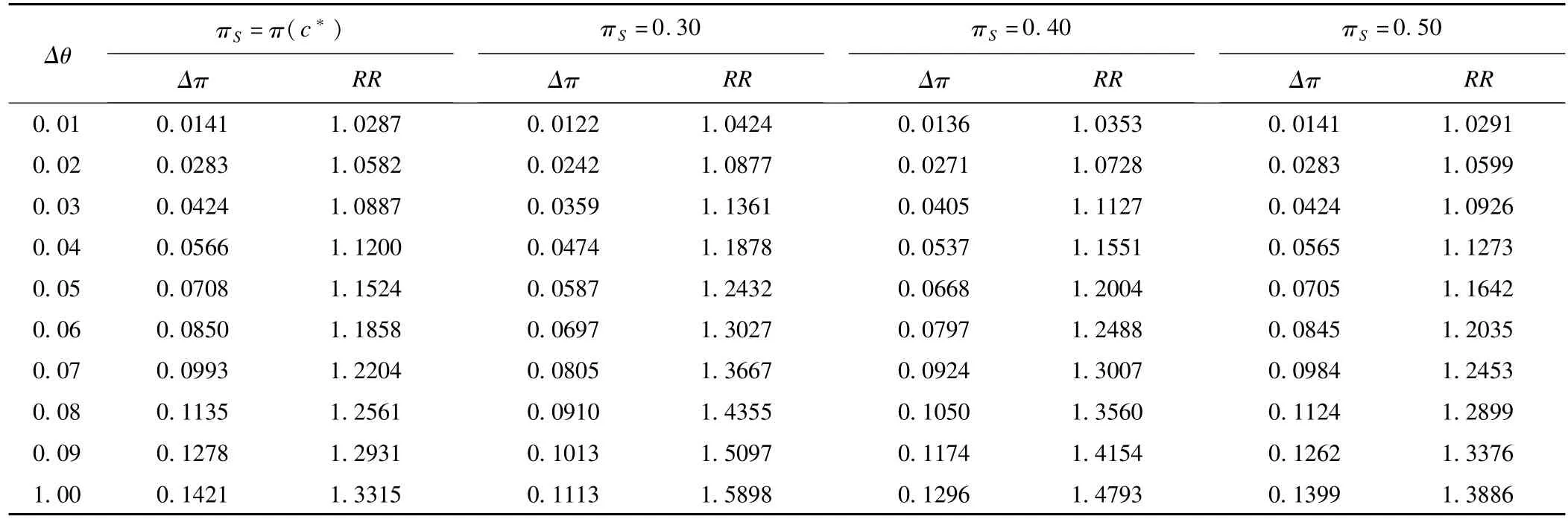
表1 双正态分布P-P曲线下面积θ与Δπ之间的数量关系

表1 双正态分布P-P曲线下面积θ与Δπ之间的数量关系（续）

3.P-P曲线下面积的计算

P-P曲线计算有多种方法，这里给出最基本的方法。可以证明，P-P曲线下面积是对照组检测值大于试验组检测值的概率，即

θ的估计值可以利用下式计算，即

其中

nS和nS为标准组和试验组的检测例数。样本估计方差可以用Delong给出的非参数方法计算得到［4］。

4.统计检验方法

对于给定的P-P曲线下面积的非劣效界值δP-P，非劣效检验的方法为［5］

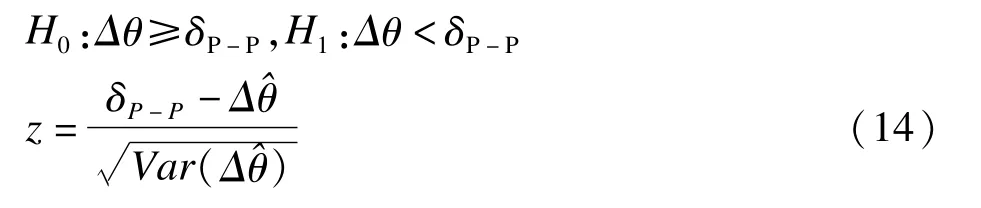
统计量z近似服从正态分布，如果z＞z1-α，则可以拒绝H0，认为试验组非劣效性成立。同样可以使用可信区间的方法，即按照100（1-α）%的置信度，计算出单侧可信区间的上限CU，若CU＜δP-P则可下非劣效的结论。可信区间检验方法与公式（11）检验方法等价。

P-P曲线方法的检验效能

1.双正态分布情况

在两组方差相同的情况下，两组均数非劣效检验的样本含量计算公式为［6］

其中，δ0和Δμ分别为给定的两组均数差值的允许界值和实际差值，p为标准组在总样本中所占的比例。

对于给定的P-P曲线检验方法的非劣效界值δP-P，与两组均数差值的非劣效检验的界值δ0有如下关系：

μT．0是在原假设H0：Δθ＝δP-P成立时试验组的均数。容易推出：

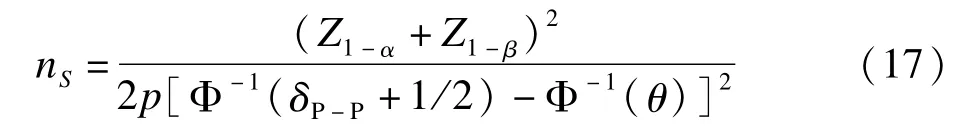
为便于比较，选择P-P曲线方法检验，取δP-P＝0.05和δP-P＝0.07两种不同的非劣效界值，两组的样本含量比值k＝1，即p＝1/2，样本量nS＝nT＝200，对于不同实际差别Δθ，其检验效能的变化见图3。可以看出，在两组服从正态分布且方差相同假定下，P-P曲线方法与传统的均数差值方法的检验效能曲线重合。

2.偏态分布情况

假设测量结果Y取对数lnY服从正态分布，即lnY～N（μ，σ2）。如果标准组和试验组的测量结果分别服从则Y的数学期望为

根据设定的P-P曲线下面积非劣效界值δP-P，将其换算成用原始变量Y表示的非劣效界值δ0，具体方法为

其中E（YT．0）和μT．0分别表示在原假设成立条件下，试验组测量值和取对数的期望值。

图3 正态分布下采用两种不同检验方法计算出的检验效能（传统方法的检验界值δ0按照P-P曲线检验给出的界值δP-P换算得到）

用模拟实验考核检验效能，模拟中设lnYS～N（2，1）和lnYT～N（μT．alt，1），μT．alt是备择假设下试验组测量值对数的期望值。模拟试验采用传统的均数差值法和P-P曲线两种方法进行检验（α＝0.05），结果见图4。结果表明，随着Δθ的增大，非劣效检验的把握度逐渐减小，在实际差别与非劣效界值相同时，检验效能接近检验水准0.05，说明能够较好地控制检验的Ⅰ类误差。同时也看出，在偏态分布情况下，P-P曲线法的结果与正态分布时的检验效能比较十分相近，而传统的均数差值法的检验效能则降低很多，P-P曲线检验方法的检验效能明显高于传统检验方法。

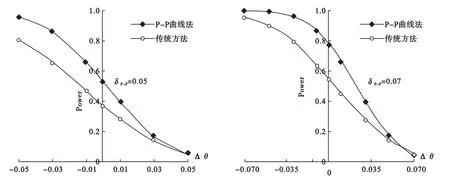
图4 在对数正态分布下采用两种不同检验方法计算出的检验效能（传统方法的检验界值按照P-P曲线检验给出的界值换算得到）

讨 论

1.本文针对两组计量资料的非劣效性评价问题，给出了一种新的统计检验方法。P-P曲线的思想源于诊断试验评价的ROC（receiver operating characteristic）分析，这种方法的最大特点是对数据的分布没有任何限制，而且对于不同检测的数据使用相同的统计准则去确定非劣效性界值δP-P，并且可以将试验组和标准组的分析结果用图形直观的显示。

2.实际中，非劣效性界值的选择需要根据统计学和临床判断综合考虑，本文推荐使用δP-P＝0.05，如果放宽检验标准，可以选择δP-P＝0.07，给出的这些标准不仅适合正态分布，同样适合偏态分布数据。在双正态分布时，由式（4）可以导出；δP-P＝Φ（δ0/由此可见，δP-P＝0.05时，σS和σT的值愈大，δ0也愈大，即这种方法能够自动地调整δ0与数据变异之间的关系，使非劣效性评价更为简单和具有实效。这种方法的不足：Δθ的实际意义不如Δμ直观，因此建议在Ⅱ期探索性临床试验中使用。

3.模拟试验的结果表明，无论总体是否服从正态分布，只要方差相同，检验效能基本不改变，而传统方法只有在正态和方差相同条件下才能够准确地检验和保证最大的检验效能。事实上，在方差不相同时，P-P曲线方法同样是有效的，但在这种情况下需要考虑其专业意义。

4.关于协变量调整的问题。对计量数据的非劣效性试验，如果有协变量影响疗效，可以采用协方差分析的方法，然而如果数据呈明显的偏态分布或是两组方差不相等，则传统的协方差分析的检验结果可能出现问题。本文给出的P-P曲线方法同样可以对协变量进行调整分析［3，6］，并且没有线性模型对这些条件的限制，同时可以很容易地推广到重复测量等研究设计的非劣效性分析，具有一定的研究价值和应用前景。

1.CCTS工作组，夏结来.非劣效临床试验的统计学考虑.中国卫生统计，2012，9（2）：270-273.

2.侯艳，武振宇，李康.临床新药试验中非劣效性检验界值的确定方法.中国卫生统计，2008，25（6）：648-651.

3.Hou Y，Ding V，Li K，Zhou XH.Two new covariate adjustmentmethods for non-inferiority assessment of binary clinical trials data.Journal of Biopharmaceutical Statistics，2010，21（1）：77-93.

4.DeLong ER，DeLong DM，Clarke-Pearson DL.Comparing the areas under two or more correlated receiver operating characteristic curves：A nonparametric approach.Biometrics，1988，44：837-845.

5.刘玉秀，姚晨，陈峰，等.非劣性/等效性试验的样本含量估计及统计推断.中国新药杂志，2003，12（5）：371-376.

6.侯艳，李康.非劣效性临床试验中两组率差值的协变量调整方法.中国卫生统计，2012，29（2）：196-198，201.

（责任编辑：郭海强）

P-P Curve Evaluation M ethod for the Non-inferiority of Clinical Trials in the Quantitative Data

Hou Yan，Li Kang（Department of Medical Statistics，Harbin Medical University（150086），Harbin）

ObjectiveIn this study，we presented a new statistical method to assess the non-inferiority for two-arm quantitative outcome.MethodsEfficacy rates from the test drug and positive control group were obtained according to the thresholds formed a probability and probability（P-P）curve，where the horizontal axis is the efficacy rate from the positive control drug and the vertical axis is one from the test drug.We calculated the area under the P-P curve and performed the statistical testw ith this new-devised statistics.In addition，a series of simulation studieswere performed to test the statistical power for this method.ResultsWe presented a test formula for P-P curvemethod，which is easier to choose the non-inferiority margin.Furthermore，thismethod has no lim itation for the data distribution，especially in the case of skewed distribution，it could provide high statistical power for thismethod.ConclusionThismethod could be effective in the explorative study and it deserves practical application and further studies.

Clinical Trials；Non-inferiority Test；Non-inferiority Margin；P-P curve

*：国家自然科学基金项目（81102201），哈尔滨医科大学伍连德青年基金（WLD-QN1105）

Δ通信作者：E-mail：likang＠ems.hrbmu.edu.cn