复杂抽样数据多水平模型分析方法及其应用
2014-03-10于石成廖加强于妺郭莹肖革新金承刚冯国双胡跃华马林茂
于石成廖加强于 妺郭 莹肖革新△金承刚冯国双胡跃华马林茂
复杂抽样数据多水平模型分析方法及其应用
于石成1廖加强2于 妺1郭 莹1肖革新1△金承刚3冯国双1胡跃华1马林茂1
目的本文通过抽样调查实例,阐述多阶段抽样、不等抽样概率和事后分层特性不同产生的复杂抽样数据,其应用多水平模型分析的原理和方法。方法对我国某省行为危险因素抽样调查的数据,应用未加权和加权的随机截距logistic回归模型分析了某些因素与跌倒性伤害的关系。结果实际分析包括50个区县(PSU),250个乡镇街道(2水平),12086个体(1水平)。未加权估计结果显示:对跌倒性伤害有统计学影响的变量是健康状况中等和差、未被雇佣和未婚,年龄为负相关,即年龄越大,发生跌倒性伤害的危险性越小;复杂抽样2水平logistic回归分析显示:对跌倒性伤害有统计学影响的变量与未加权的结果基本一致,但未婚失去了统计学意义。体重指数、性别和受教育程度与跌倒性伤害的发生没有统计学联系。结论与未加权的结果比,加权分析对跌倒性伤害有统计学影响的变量基本一致,但加权复杂抽样PMLE估计的标准误偏大,结果更保守;对性别的分析发现,加权后的结果符合目前对跌倒性伤害发生机制的认识,因此纳入权重的多水平分析方法对该资料可能更合理。
复杂抽样 多水平模型 多阶段抽样 随机效应logistic回归
目前主流统计分析软件,如SAS,SPSS,Stata,MPlus和SUDAN,都将抽样权重纳入统计分析过程,除可进行复杂抽样数据的描述性统计分析外,还可进行复杂抽样数据的多元线性回归、logistic回归、Poisson回归和Cox回归等,使得复杂抽样数据的统计推断方法越来越多地在数据分析中得到应用[1-4]。复杂抽样数据大多具有层次结构即多水平,其特点是反应变量的分布在个体间不具独立性,存在地理距离内、行政区划内或特定空间范围内的聚集性[5]。多水平模型在医学领域已有多年的应用,在处理层次结构数据上已发挥了重要的作用[6-8];复杂抽样数据的分析既要考虑抽样权重,又要兼顾数据的层次结构,一般是将权重纳入广义线性混合模型(generalized linearm ixed models,GLMMs)来处理这类数据[9-11]。当GLMMs将抽样权重纳入模型后,使GLMMs能处理复杂抽样数据,解决了复杂抽样数据多水平模型统计分析和计算问题。鉴于目前我国全国性的流行病学抽样调查多采用多阶段抽样设计,并且数据具有层次结构,因此复杂抽样数据的多水平模型分析已有明显的应用价值。
多水平复杂抽样数据的线性模型,Pfeffermann应用伪最大似然估计(pseudo-maximum-likelihood estimation)算法来估计模型的参数,效果很好。但对广义线性混合模型(generalized linearm ixed models),认为较好的模型估计方法是全伪最大似然估计(full pseudo-maximum-likelihood estimation),它应用自适应积分法(adaptive quadrature)估计模型参数,标准误的估计采用泰勒线性化三明治估计量[10]。目前国外复杂抽样数据多水平模型理论和应用研究已有二十几年的历史,我国在这方面的理论研究鲜有报告,可能由于数据本身和应用的限制,在医学研究领域国内还没有应用复杂抽样多水平模型来处理流行病学抽样调查数据。本文介绍了复杂抽样数据多水平模型分析的原理和方法,并用STATA软件对我国某省行为危险因素调查的数据拟合复杂抽样数据多水平模型,并与未考虑复杂抽样的多水平模型结果进行了比较和解释,以阐述具有层次结构的复杂抽样数据应用复杂抽样数据多水平模型的合理性。
模型基本原理
广义线性混合模型参数估计构造一个常边际对数似然函数(usualmarginal log likelihood function),其公式如下:
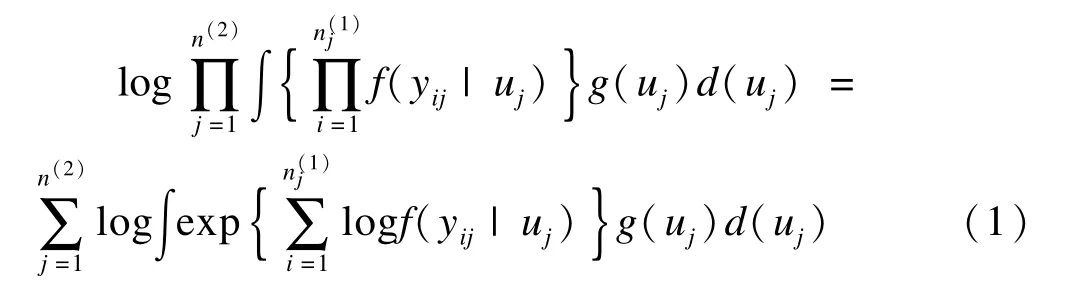
复杂抽样数据的广义线性混合模型参数估计构造一个加权对数伪似然函数(log pseudo-likelihood function w ith weights),其公式如下:
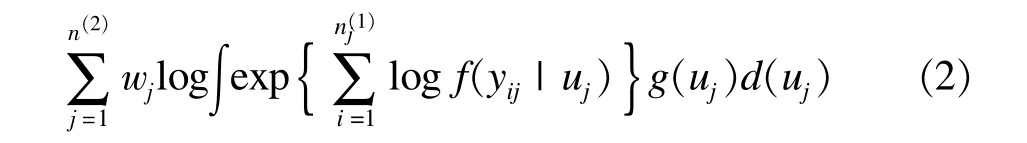
这里,wj=1/πj,wi|j=1/πi|j,i和j分别代表1水平个体和2水平的层。一般情况下,复杂抽样数据多水平模型采用牛顿-拉夫逊最大算法(New ton-Raphson maximum algorithm)使加权对数伪似然函数达到最大值,即PMLE(pseudo-maximum-likelihood estimation)参数估计值;其标准误估计采用泰勒线性化三明治估计量(sandw ich estimator)。
复杂抽样数据广义线性混合模型用上式(2)做PMLE估计时,须考虑2水平权重;且不能直接使用1水平的个体权重,这样可能影响参数估计的准确性[11],解决方法是对1水平个体权重进行权重的缩放(scaling of weights)。Longford等[12]1995年提出的权重缩放方法1如下:

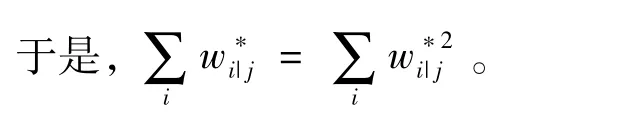
1998年Pfeffermann等[13]提出了权重缩放方法2如下:

应用实例及结果解释
我国某省在2010年进行了行为危险因素的调查,该省共有150个区县,1900个乡镇,人口7000多万。根据计算本调查所需样本量为15000人,使用了三阶段整群抽样设计,第一阶段随机抽取区县,第二阶段抽取乡、镇和街道,第三阶段抽取个体。第一阶段随机抽取产生了50个区县(primary sampling units,PSU);第二阶段,在每个区县内按乡、镇、街道分层,在每层内按概率比例规模抽样(PPS)方法,整群抽取2个乡、1个镇和2个街道,共产生了250个乡镇街道;在抽取的每个乡、镇和街道中,随机抽取60名年龄45岁及以上的成年人,共15000个体。该调查将在过去的3个月内发生1次或2次及以上跌倒性伤害为反应变量,记为1,未发生任何跌倒性伤害为0,反应变量为二分类变量,可用复杂抽样logistic回归分析该数据;但该数据显然具有地区和个体的层次结构,因此,合适的统计分析方法应是考虑复杂抽样2水平logistic回归模型。这里个体为1水平,250个乡、镇、街道为2水平,最高水平区县(PSU)在这里不作为水平考虑,但在分析中可作为层变量进行调整处理。
本文分析了跌倒后造成的伤害与体重指数(BM I)及一些感兴趣变量的关系,因变量为在过去三个月内是否发生过跌倒性伤害,自变量有体重指数、性别、年龄、健康状况、受教育程度、雇佣状况和婚姻状况等7个变量。该数据拟合复杂抽样2水平随机截距logistic回归模型,分析了250个乡、镇和街道,由于有缺失数据,实际分析的样本量为12086例。
调查采用了不等概率抽样,需要根据抽样设计对样本进行抽样加权,加权过程涉及到个体抽样权重,未包括不应答权重和事后分层加权。三阶段抽样,用w代表权重,脚注1、2和3分别代表县、乡镇街道和个体各阶段的抽样权重,用i表示某一样本个体,s代表某一样本个体所在的层。样本区县的抽样权重(wsi1)值为分层简单随机抽样下样本区县抽样概率的倒数,其计算公式如下:
样本乡镇街道的抽样权重(wsi2)值为与人口数成比例的PPS抽样下样本乡镇街道抽样概率的倒数,用下式计算:

样本个体的抽样权重(wsi3)值为样本个体抽样概率的倒数。可计算如下:

依据上述各阶段抽样权重,最终样本个体的抽样权重为下式(5):
wsi=wsi1×wsi2×wsi3=样本个体i所在区县分层抽样比倒数×

样本个体i所在乡镇街道45岁及以上人口百分比构成,如无法得到实际数据,可用该县或省的构成(Pop45)计算。
计算乡镇街道(2水平单位)πj,个体被抽中的概率πij及它们的权重,即概率的倒数,其计算公式为:
ws2=wsi1×wsi2=样本个体i所在区县分层抽样比倒数×

Stata提供了分析复杂抽样2水平随机截距logistic回归模型的分析模块gllamm和说明书,其未加权最大似然估计(MLE),stata分析语句为:gllamm injury bmi age gender health marriage education employed,i(ID_level_2)link(logit)fam ily(binom)nip(12)adapt
稳健标准误估计(Robust standard errors):gllamm,robust
其加权伪最大似然估计(PMLE)stata分析语句为:
gllamm injury bm i age gender health marriage education employed,i(ID_level_2)cluster(w t2)link(logit)family(binom)pweight(w t1_sw)nip(12)adapt
调整PSU后的稳健标准误估计:gllamm,robust cluster(psu)
其中,因变量为二分类injury,自变量有:体重指数BM I(哑变量)、健康状况health(哑变量)、婚姻状况marriage(哑变量)、受教育程度education(哑变量)和雇佣状况employed(哑变量)。i指出2水平变量为ID_level_2;cluster定义2水平变量的权重为w t2;link指出连接函数为logit;family指出拟合二项分布(binom),若拟合Poisson分布,则family(Poisson);pweight定义1水平个体权重为w t1_sw,其为经缩放后的值。前面提到1水平权重不能直接应用,要进行权重的缩放,下面是应用式(3)和(4)两种权重缩放方法的stata语句。
方法1:

方法2:

应用2水平随机截距logistic回归模型分析了乡镇街道(2水平)的个体(1水平)跌倒性伤害与感兴趣的因素关系,用区县变量(PSU)分层调整。分析时没有将区县作为一个水平来对待,主要考虑区县的变异可能不大,但在标准误估计时,调整了区县(PSU)的聚集效应。由于缺失数据的存在,最终的分析在50个PSU,250个乡镇(2水平)和12086个体(1水平)中进行;最终结果报告了未加权2水平logistic回归的参数估计-基于模型标准误估计和稳健标准误估计,以及应用权重缩放方法的PMLE参数估计,结果见表1。从表1可见,未加权2水平logistic回归的参数估计,基于模型和稳健标准误估计结果很接近,对跌倒性伤害有统计学显著影响的变量:健康状况中等和差、未被雇佣和未婚,年龄为负相关,即年龄越大,发生跌倒性伤害的危险性越小;复杂抽样2水平logistic回归参数PMLE估计,权重缩放方法1和2估计结果非常接近;与未加权的方法比,对跌倒性伤害有统计学显著影响的变量与未加权的结果基本一致,但未婚失去了统计显著性,两种缩放方法估计的P值在0.05~0.10之间。其它分析变量,如体重指数、性别和受教育程度与跌倒性伤害的发生没有统计学联系。加权复杂抽样PMLE估计,大多数参数估计值比未加权估计增加,但其标准误比未加权估计值增加明显,导致大部分变量P值增大,估计保守。
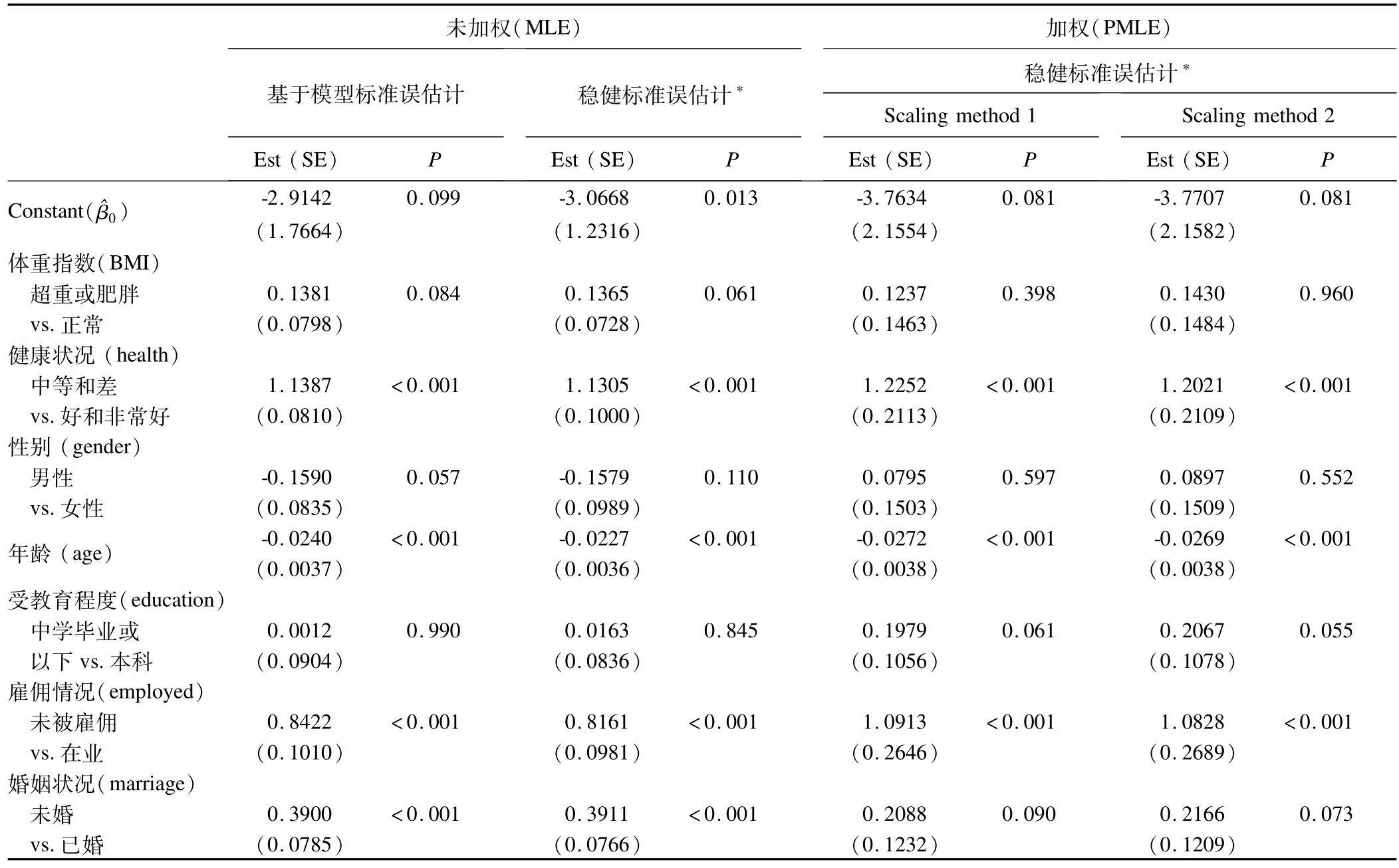
表1 2水平随机截距logistic回归和复杂抽样2水平随机截距logistic回归拟合
讨 论
流行病学抽样调查一般应用多阶段抽样,第一阶段先抽取地区或群(clusters),第二阶段抽取群下面的亚群(subclusters);最后阶段抽取基本抽样单位,如个体。这种抽样方法产生了多水平数据,基本抽样单位为1水平或最低水平,最高水平为PSU。对这类资料的分析不但考虑复杂抽样的权重(包括抽样权重、不应答权重和事后分层权重),而且考虑数据的多水平结构,即应用复杂抽样数据多水平模型分析方法。本文应用我国某省行为危险因素调查的数据,应用Rabe-Hesketh描述的考虑权重的全PMLE参数估计方法,通过适应积分法估计任何水平模型的参数和标准误。Stata软件gllamm程序分析发现:健康状况中等和差、未被雇佣和未婚与跌倒性伤害的关系与以前的文献或研究一致[14];但一般认为年龄大发生跌倒性伤害的可能性大[15],但本结果与之相反,这也许与本研究选取的个体年龄大有关。文献认为男性较女性更易发生跌倒性伤害[16],本研究未加权的分析结果是男性发生跌倒性伤害的危险性小;加权的2水平随机截距logistic回归模型显示男性与跌倒性伤害是正相关;虽然加权和未加权的结果均没有统计显著性,但加权后的结果合理,符合目前对跌倒性伤害发生机制的认识。这也部分说明了复杂抽样的层次结构数据,分析时纳入权重的多水平分析方法的合理性。
复杂抽样数据的统计分析也有百年的历史[17],1990年代以后更有新统计理论和方法发展,复杂抽样的统计方法已包括:列联表资料的对数线性模型和相关的方法、广义线性模型(logistic回归和Poisson回归)、生存分析、一般线性混合模型、结构方程模型、隐变量模型,这些方法充分考虑了抽样权重,对参数标准误和可信区间的估计更准确。目前SAS、Stata、SPSS和SUDAN统计软件包都包含了复杂抽样数据的统计描述、一般线性回归、logistic回归(二分类、有序和无序)、Poisson回归(零膨胀、负二项)、生存分析等,可以满足大部分复杂抽样数据的统计分析。
但是目前流行的统计软件还都没有包括复杂抽样多水平模型拟合程序。当抽样权重纳入模型时,一般构造伪似然函数(pseudo-maximum-likelihood)来估计模型参数。在实践中的一个主要问题是大多数流行病学抽样调查仅给出了基本抽样单位或1水平的抽样权重,而没有高水平的权重;但在进行复杂抽样数据多水平模型拟合时,需要高水平的抽样权重。因此,在今后的流行病学调查设计中和实施时,应注意收集计算各水平权重指标数据,以便在数据分析时做加权处理。
1.Rao JNK.Interplay between sample survey theory and practice;anappraisal.Survey Methodology,2005,31:117-138.
2.吕筠,何平平,李立明.复杂抽样调查数据实例分析.中华流行病学杂志,2008,29(8):832.
3.缪凡,童峰.复杂抽样数据的logistic回归分析方法及其应用.中国卫生统计,2008,25(6):577-579.
4.胡跃华,匡翔宇,金承刚,等.复杂抽样Poisson回归分析方法及应用.中国卫生统计,2012,29(5):650-653.
5.杨珉,李晓松主编.医学和公共卫生研究常用多水平统计模型.北京,北京大学医学出版社,2007.
6.贾改珍,闫阳,徐天和,等.多水平模型在大学生预防艾滋病健康教育影响因素分析中的应用.中国卫生统计,2013,30(1):37-39.
7.Gebremariam MK,Andersen LF,Bielland M,et al.Does the school food environment influence the dietary behaviours of Norwegian 11-yearolds.The HEIA study.Scand JPublic Health,2012,40(5):491-497.
8.Nansel TR,Lipsky LM,Lannotti RJ.Cross-sectional and longitudinal relationships of bodymass index with glycemic control in children andadolescentswith type 1 diabetesmellitus,2013,100(1):126-132.
9.Steven G.Heeringa,Wagner J,Torres M,et al.Sample designs and samplingmethods for the Collaborative Psychiatric Epidem iology Studies(CPES).Int.J.Methods Psychiatr.Res.,2004,13(4):221-240.
10.Sophia Rabe-Hesketh.Multilevelmodeling of complex survey data.J. R.Statist.Soc.,2006,169:805-827.
11.Moshe Feder,Gad Nathan,Danny Pfeffermann.Survey Methodology,2000,26(1):53-65.
12.Longford NT.Model-basedmethods for analysis of data from 1990 NAEP Trial State Assessment.Research and Development Report NCES 95-696.Washington DC:National Center for Education Statistics.
13.Pfeffermann D,Holmes CJ,Goldstein DJ,et al.Weighting for unequal selection probabilities in multilevelmodels.J.R.Statist.Soc.B,1998,60:23-40.
14.Roe B,Howell F,Riniotis K,et al.Older people and falls:health status,quality of life,lifestyle,care networks,prevention and views on service use follow ing a recent fall.JClin Nurs,2009,18:2261-2272.
15.Hausdorff JM,Rios DA,Edelberg HK.Gait variability and fall risk in community-living older adults:A 1-year prospective study.A rch Phys Med Rehabil,2001,82:1050-1056.
16.Stevens JA,Sogolow ED.Gender differences for non-fatal unintentional fall related injuries among older adults.Injury Prevention,2005,11:115-119.
17.Fisher RA.StatisticalMethods for Research Work.Oliver and Boyd,Edinburgh,1925.
(责任编辑:刘 壮)
App lication of M ultilevel M odeling to Com plex Sam ple Survey Data
Yu Shicheng,Liao Jiaqiang,Yu Mo,et al(Chinese Center for Disease Control and Prevention(102206),Beijing)
ObjectiveTo illustrate the principal and application ofmultilevelmodeling of complex survey data thatwere derived from multistage sampling,unequal sampling probabilities and different features of post-stratification.MethodsWeighted and un-weighted random intercept logistic regressionmodelswere applied to complex survey data of behavioral risk factors in a province to look at the association of fall injuries w ith some factors of interest.ResultsThere were 12086 subjects(level 1)aged 45 years or above nested w ithin 250 villages,towns and sub-districts(level 2)from 50 counties/districts(PSU).Un-weighted results showed that variables significantly and positively associated w ith the risk of fall injurieswere fair or poor health,unemployed situation,unmarried;age was significantly and negatively associated w ith the risk of fall injuries,or one less likely got injured when getting older.The results from 2-level random intercept logisticmodel demonstrated that the variables associated w ith the risk of fall injuries were sim ilar to those from un-weighted models,but the variable of unmarried m itigated its significance to be insignificant.Body mass index,beingmale,educational levelwere notassociated w ith the risk of fall injuries from the analyses.ConclusionIn contrast to the results from un-weighted methods,statistically significant variables from weightedmethodswere analogous to those from weighted ones;however,estimates using full pseudo-maximum-likelihood estimation(PMLE)weremore conservative as opposed to un-weighted ones.As for gender,weighted result was in consistent w ith the currentunderstanding of themechanism for the developmentof fall injuries,therefore,it soundedmore reasonable to employ multilevel modeling for the complex survey data.
Complex survey data;Multilevelmodel;Multistage sampling;Random intercept logistic regression
*:淮河流域癌症综合防治项目(1310800003)
1.中国疾病预防控制中心公共卫生监测与信息服务中心(102206)
2.四川大学华西公共卫生学院卫生统计教研室(610041)
3.北京师范大学社会发展与公共政策学院(100875)
△通信作者:肖革新,E-mail:biocomputer@126.com
