三种模型对广东省伤寒副伤寒逐月发病数预测的比较*
2014-03-10骊钱俊杨军欧春泉
李 骊钱 俊杨 军欧春泉△
三种模型对广东省伤寒副伤寒逐月发病数预测的比较*
李 骊1钱 俊2杨 军1欧春泉1△
目的应用三种统计模型预测伤寒副伤寒的发病趋势,比较其预测效果,为伤寒副伤寒的预测和防控提供科学依据。方法利用广东省2008年5月至2012年4月四年的伤寒副伤寒逐月发病资料,分别拟合季节性综合自回归滑动平均(SARIMA)模型、经傅里叶季节性调整的综合自回归滑动平均(FARIMA)模型和动态谐波回归(DHR)模型,并用前面建立的三种模型预测后续半年(2012年5月—2012年10月)的逐月发病数。结果伤寒副伤寒的发病有明显的周期性和季节特征,周期为1年,7-8月份为发病高峰期。流行强度和流行高峰出现的月份均存在一定的年度差异。三种模型拟合四年的伤寒副伤寒发病情况,其平均绝对百分比误差(MAPE)依次为:DHR模型(7.8%)<FARIMA模型(12.9%)<SARIMA模型(13.4%);三种模型预测后续半年的发病情况,其MAPE依次为:DHR模型(3.5%)<FARIMA模型(5.6%)<SARIMA模型(6.8%),其他模型评价指标结果也类似。结论三种方法均有较佳的预测效果。相对而言,DHR的预测精度更高。本研究可为常见传染病的预测提供一定的方法学参考。
SARIMA模型 FARIMA模型 DHR模型 预测 伤寒副伤寒
伤寒副伤寒是我国法定的乙类传染病。在世界范围内,该病是导致死亡的重要原因[1]。本病亦是我国常见的肠道传染病之一,在我国终年散发,部分地区出现暴发流行[2-3]。其传染性强、病程长、易复发、并发症多、疾病负担较重[4]。由于流动人口增加、耐药菌株增多等问题的出现使其防控难度进一步增加,因而有效地预测伤寒副伤寒的发病情况,对于卫生管理部门及时做好预防干预措施具有重要意义。SARIMA模型是分析时间序列的经典时间域方法。FARIMA模型和DHR模型则是时间域与频率域相结合的方法,二者能结合时间域与频率域两类时间序列分析方法的优势,国内尚未有研究使用此两种方法预测传染病的发病。笔者试构建以广东省2008年5月至2012年4月伤寒副伤寒逐月发病数据为基础的FARIMA模型和DHR模型,并将二者与常用的SARIMA模型进行比较,探讨伤寒副伤寒预测的优化模型,为建立该病的预测系统提供科学依据,同时也为其他传染病的预测提供思路。
资料与方法
1.资料来源
从广东省卫生厅官方网站获得全省2008年5月至2012年10月期间伤寒副伤寒逐月发病资料。广东省有很好的传染病监测系统,保证了本研究资料的可靠性。
2.统计方法及建模过程
基于2008年5月至2012年4月伤寒副伤寒逐月发病数据建立以下三种模型,用2012年5月至2012年10月的数据对模型的预测效果进行评价。
(1)SARIMA模型[5]
SARIMA模型的构建分以下几个步骤实现:
①对数据进行预处理,即:xt=lnyt,其中yt为待分析的时间序列。
②模型识别,即根据自相关(ACF)图,偏自相关(PACF)图及AIC最小化准则确定模型。
③参数估计,并检验参数是否有统计学意义。
④模型诊断及预测,通过判断残差序列是否为白噪声和存在自相关性评价模型是否合适。用确定的模型进行预测。
(2)FARIMA模型
傅里叶方法的主要原理是用一系列正弦或余弦波近似拟合原始序列的波谱,本例以此拟合序列的季节组分,即:

其中period表示序列周期,本例由于伤寒副伤寒发病数呈现明显的12个月周期,故设为12;t表示第t月,取值为1,2,…,n,n表示待分析时间序列的长度;terms通常取小于等于period/2的整数。对数据进行季节性调整后构建ARIMA模型。
(3)DHR模型[6-7]
动态谐波回归(dynamic harmonic regression,DHR)模型是单变量UC(unobserved component)模型的特例,本研究采用的DHR模型为:

其中xt是经处理的时间序列,Tt代表趋势组分或低频组分,St表示季节性周期组分。et为残差,经常将其假设为服从均数为0,方差为σ2的正态分布。由于Tt和St不能直接由原始数据得到,故将该模型称为UC模型。UC模型的各组分可由状态空间模型来表达。在DHR建模中,我们将用到广义随机游走(GRW)类模型。最一般的GRW类模型定义为:

其中,x1,t,x2,t分别是各组分的变化水平和斜率。η1,t,η2,t是对角协方差阵为常量的正态随机变量。GRW的主要取值方式有随机游走(RW)模型:α=1,β=γ=0,η2,t=0;整合随机游走(IRW)模型:0<α<1,β=γ=0,η2,t=0等。
在DHR模型中,各组分可由时变参数(TVP′s)表示,这些参数可以采用最优卡尔曼滤波(KF)和固定间隔平滑(FIS)方法估计。在估计TVP′s时,需先确定诸如噪声方差比例(NVR)这些超参数,超参数则采用频率域的方法进行估计。
本研究DHR建模分以下几个步骤实现:
①对数据进行预处理,即:xt=lnyt,其中yt为待分析的时间序列。
②估计处理后序列的经验谱。根据AIC最小化准则,自回归谱阶数设为24。
③通过分析自回归谱,确定谐波频率。
④估计噪声方差比例及超参数 IRW模型适用于表达缓慢变化的情况,RW模型适用于表达变化快速的情况[6]。故Tt和St的拟合分别采用IRW和RW模型。
⑤利用第④步估计得到NVR和其他超参数,由最优卡尔曼滤波和固定间隔平滑法实现每个组分的估计及预测功能。
(4)模型评价指标
采用以下指标评价模型的预测准确性:均方根误差(RMSE),平均绝对误差(MAE),平均绝对百分比误差(MAPE)及平均绝对偏差百分比(PMAD)。各指标的计算方法如下:
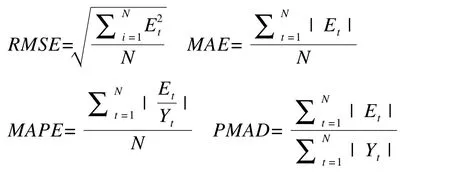
其中,N表示待分析时间序列的长度;Et表示拟合或预测误差,即实测值与预测值之差;Yt为时间序列的实测值。
(5)统计软件
SARIMA和FARIMA建模采用R 2.15.1,DHR建模采用MATLAB 7.6编程实现。
结 果
1.发病趋势分析
2008-2012年广东省伤寒副伤寒每月发病数见图1。由图可以看出,伤寒副伤寒的发病有明显的周期性和季节特征,周期为1年,7~8月份为发病高峰期,而其他月份也存在一定的病例数。流行强度和流行高峰出现的月份均存在一定的年度差异,2008-2009年高峰出现在7月,2010-2012年流行高峰在8月份。2010年的发病人数最多,季节性高峰最明显,全年累计发病数为1828例,2011年又下降至2008年的水平,2012年前三季度总的发病数与2011年基本持平,但1~3月的发病数较2011年高。

图1 伤寒副伤寒发病数时序图
2.各模型构建结果
(1)SARIMA模型
对处理过的序列进行单位根检验,可知序列不平稳。进一步对序列xt进行一次季节性差分后序列平稳。观察SARIMA(0,0,0)×(0,1,0)12残差序列的ACF和PACF图(图2),提示宜采用乘积混合效应模型SARIMA(1,0,0)×(0,1,0)12。模型残差序列的ACF和PACF图(图2)提示模型已经很好地消除了序列的自相关特性,能较好地拟合该时间序列。模型参数为:φ1=-0.504,拟合模型如下:
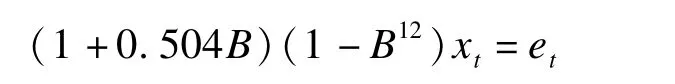
对系数进行t检验,得t=3.603(P=0.000),说明该系数有统计学意义。模型残差通过了Ljung-Box检验,说明残差为白噪声。将上式展开,得:

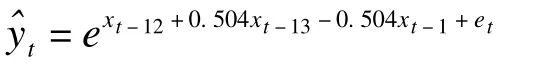
(2)FARIMA模型
首先建立只包含傅里叶项的模型,本例terms取1。
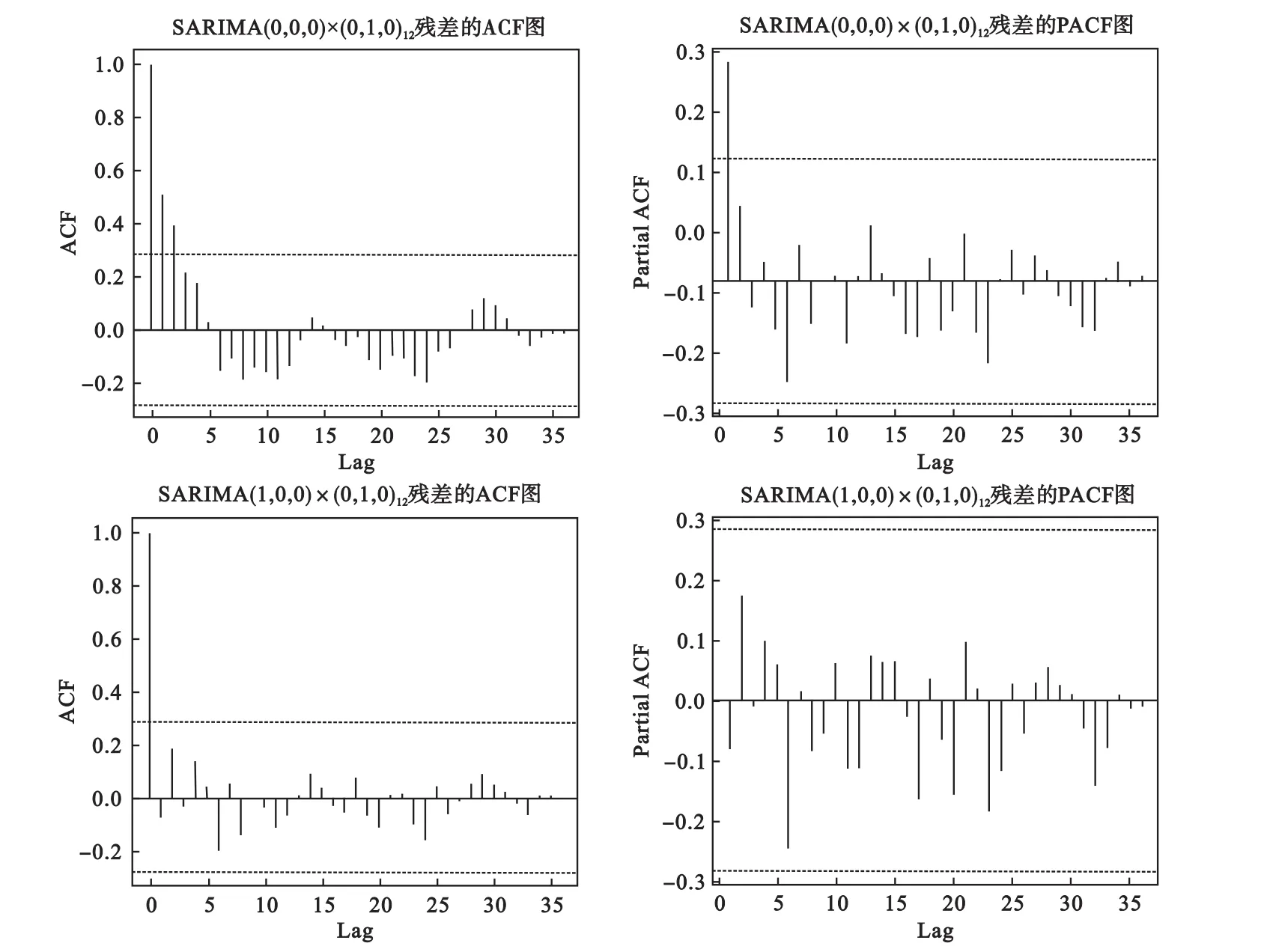
图2 SARIMA(0,0,0)×(0,1,0)12残差和SARIMA(1,0,0)×(0,1,0)12残差的自相关和偏自相关图
对模型的残差进行单位根检验,可知残差序列不平稳,对残差进行一阶差分后序列平稳。观察FARIMA(0,1,0)残差序列的ACF和PACF图并依据AIC最小化准则选定最终模型FARIMA(0,1,1)。模型参数为:θ1=-0.568,a1=46.419,b1=-15.676,即得到模型:
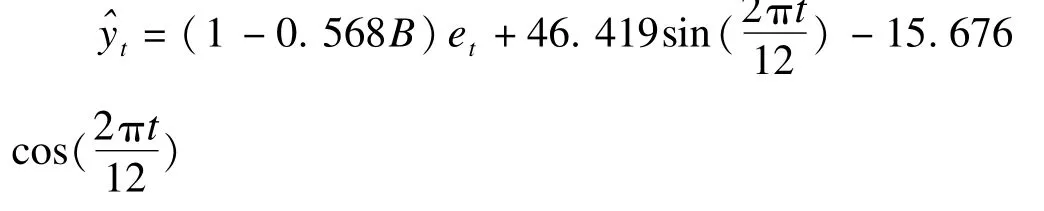
对模型系数进行t检验,三者t值分别为:t=-3.611(P=0.000),t=10.053(P=0.000),t=-3.587(P=0.000),系数有统计学意义。模型残差通过了Ljung-Box检验,说明残差为白噪声。将上式展开,得到最终模型
(3)DHR模型
模型残差序列的ACF和PACF图提示模型已经消除了序列的自相关特性,残差序列通过了Ljung-Box检验,说明残差为白噪声。综上,模型能较好地拟合该时间序列。
3.拟合预测效果评价
从四年历史数据的拟合情况来看,三种模型均有较好的拟合效果,DHR模型尤为突出,平均绝对百分比误差最小(表1)。实际工作中,准确预测传染病流行高峰发生的时间和强度具有更大的公共卫生意义。由图3可见:实际数据在2009年出现双峰,其他年份均为单峰。SARIMA模型由于受前期数据的变化特征影响较大,其拟合值继2009年后在2010年仍然出现了双峰。FARIMA的拟合曲线比较平滑,对波峰和波谷的拟合欠佳,特别是2009年拟合的波峰滞后实际流行高峰一个月,而DHR模型对流行高峰出现的时间和强度均有较佳拟合效果(图3)。
用半年的数据进行前瞻性考核,同样反映DHR模型有最好的预测能力,2012年5月至10月的预测相对误差均控制在10%以内(表2),平均绝对百分比误差仅有3.5%。FARIMA和SARIMA模型的平均绝对百分比误差略大,分别为5.6%和6.8%。其他评价模型的指标也得出一致的结论(表1)。

图3 三种方法的预测结果图

表1 三种模型的拟合及预测效果比较
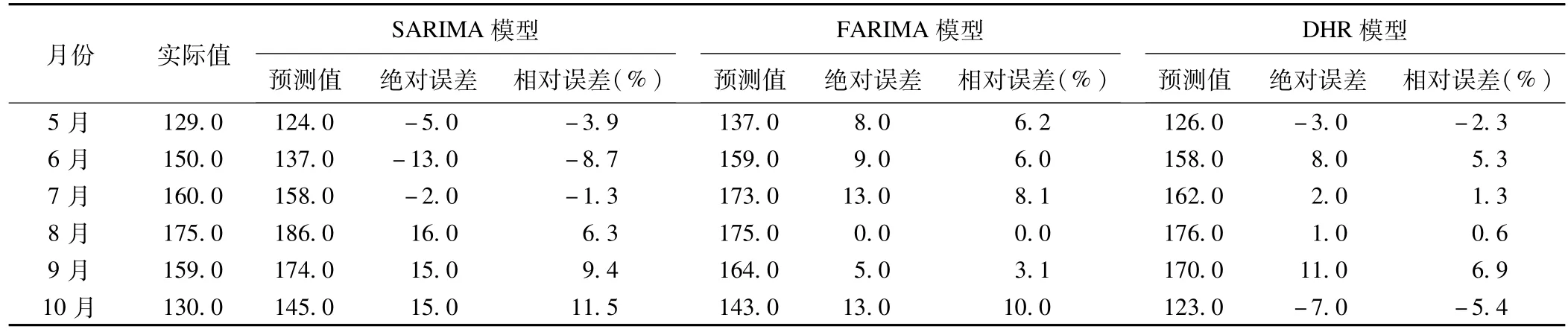
表2 三种模型的预测结果
讨 论
广东省伤寒副伤寒高发于夏秋季,发病数在7-8月达到最高峰,这与江西、云南、贵州、天津等地报道的情况类似[8-11],而印度的报道指出高峰出现在4~6月[12]。本病夏秋季高发可能是因为天气热,人们喜欢吃生冷的食物,而这些食物容易受到污染造成人的感染。另外,广东省夏秋季降水较多,强降雨等极端气候事件也会增加人群伤寒副伤寒的发病风险。2012年1~3月的发病数较2011年多,可能与当年广东省出现“回南天”有关。
在短短几年的研究时间里,一个省的总人口数通常变化较小,故往往采用逐月发病人数的时间序列数据来反映传染病发病率的变化趋势。近年来,国内有学者应用指数曲线和灰色模型预测伤寒副伤寒疫情的年度变化趋势[13-14],因而没有考虑到时序的季节性,而伤寒副伤寒发病率存在明显的季节特征,在进行逐月发病情况的预测时不容忽视。另外,有人提出用加权马尔可夫链预测伤寒副伤寒的发病情况[15],但该法只判断发病数的大致范围,没有给出具体的估计值。本研究分别采用SARIMA模型,FARIMA模型及DHR模型预测广东省伤寒副伤寒的发病情况。对三种模型的比较发现:SARIMA模型的拟合效果与预测精度较低,受前一个周期的季节性变化规律影响较大,例如:2009年伤寒副伤寒出现双峰导致2010年也错误地模拟出双峰。故当每个周期的季节性差异较大时,不建议使用SARIMA模型。在构建FARIMA模型时涉及谐波的选择,当待选谐波的个数比较多时,模型遴选较复杂,耗时较长。FARIMA模型假定序列的季节性特征不随时间变化而变化,故当各年度季节特征变化较大时,拟合效果略逊。DHR模型是一种动态拟合趋势组分和季节性周期组分的方法,它允许时间序列的季节性特征随时间变化而变化[6],故能很好地反映序列的变化特征。在本研究中,该法的拟合和预测效果最好。DHR模型的缺点在于,谐波的选择比较主观。有时根据AIC准则确定的自回归谱并不能准确地提供有意义的谐波频率信息,故在使用该法时,不能盲目地相信单个准则提供的信息,而应该结合相关专业知识和拟合结果,选择合理的参数。一般来说,传染病发病资料会呈现一定的季节性,当数据既包含长期趋势又存在季节性时,可考虑采用DHR模型对传染病的发病情况进行短期预测。当季节性不变或变化不大时,也可尝试用FARIMA模型和SARIMA模型建模。本文的预测都是基于发病数本身的,并没有考虑其他因素对发病情况的影响。事实上,传染病的发生或多或少与气象、环境等因素有一定的联系,有待将来进一步研究。也可以考虑建立一套指标体系,并通过综合运用指标体系的方法对传染病的情况进行分析和评价,确认发生危险的可能性及严重程度,决定是否发出危机报警[16]。
我国已经形成了完善的传染病监测报告体系,各级卫生管理部门及时发布统计数据,为预测模型的建立与修正提供了数据支持。本研究采用三种模型预测广东省伤寒副伤寒的发病数,分析比较了三种模型的优劣,指出DHR模型具有更好的预测准确性,为伤寒副伤寒发病情况的预报提供了科学依据,同时也为其他常见传染病的预测提供方法学的思路和借鉴。
1.Crump JA,M intz ED.Global trends in typhoid and paratyphoid Fever. Clin Infect Dis,2010,50(2):241-246.
2.天津医学院流行病学教研室主编.常见肠道传染病的防治.天津:天津人民出版社,1973:1-2.
3.卫生部疾病预防控制局,中国疾病预防控制中心主编.伤寒、副伤寒防治手册.北京:人民卫生出版社,2006:1-2.
4.王鲁茜,阚飙.伤寒、副伤寒的全球流行概况及其预防控制.疾病监测,2007,22(7):492-494.
5.彭志行,陶红,贾成梅,等.时间序列分析在麻疹疫情预测预警中的应用研究.中国卫生统计,2010,27(5):459-463.
6.Jiang B,Liang SL,Wang JD,et al.Modeling MODIS LAI time series using three statistical methods.Remote Sens Environ,2010,114(7):1432-1444.
7.Young PC,Pedregal DJ,Tych W.Dynam ic harmonic Regression.Journal of Forecasting,1999,18(6):369-394.
8.刘晓青,袁辉,王健,等.1998-2007年江西省伤寒副伤寒流行病学分析.海峡预防医学杂志,2009,15(2):27-28.
9.黄玉芬,刘志涛.云南省2008-2010年伤寒副伤寒发病情况.职业与健康,2011,27(18):2131-2132.
10.黎明,唐光鹏,姚光海,等.贵州省2004-2007年肠道传染病流行特征分析.医学动物防制,2012,28(1):5-8.
11.吴伟慎,解晓华,单爱兰,等.天津市1990-2005年伤寒副伤寒流行趋势分析.现代预防医学,2007,34(17):3304-3305.
12.Kanungo S,Dutta S,Sur D.Epidem iology of typhoid and paratyphoid fever in India.J Infect Dev Ctries.2008,2(6):454-60.
13.春雅丽,黄中敏,钱文平.应用指数曲线预测伤寒副伤寒疫情.上海预防医学杂志,2005,17(10):466-467.
14.黎景雪,王培承,邱瑞香,等.灰色模型在我国伤寒副伤寒发病率预测中的应用.数理医药学杂志,2010,23(5):506-508.
15.彭志行,鲍昌俊,赵杨,等.加权马尔可夫链在伤寒副伤寒发病情况预测分析中的应用.中国卫生统计,2008,25(3):226-229.
16.胡世雄,邢慧娴,邓志红.我国传染病的预测预警现状.中华预防医学杂志,2007,41(5):407-410.
(责任编辑:刘 壮)
Com parison of Three M odels on Prediction of Incidence of Typhoid Fever and Paratyphoid Fever
Li Li,Qian Jun,Yang Jun,et al(Department of Biostatistics,School of Public Health and Tropical Medicine,Southern Medical University(510515),Guangzhou)
ObjectiveTo compare the performance of three statisticalmethods in forecasting the incidence of typhoid fever and paratyphoid fever.MethodsUsing monthly data of cases w ith typhoid fever and paratyphoid fever in Guangdong Province from May 2008 to April2012,we fitted threemodels,including Seasonal Autoregressive Integrated Moving Average(SARIMA)model,ARIMA model applied to the seasonally adjusted data from Fourier terms(FARIMA)and Dynamic Harmonic Regression(DHR)model.Afterwards,we used the data from May 2012 to October 2012 to assess the accuracy of prediction for these threemodels.ResultsThe incidence of typhoid fever and paratyphoid fever is characterized by an apparent cyclic pattern w ith a one-year seasonal cycle.Themaximum number of cases occurred during July to August.The epidem ic strength and peak differed by years.Mean Absolute Percentage Error(MAPE)of the four-year time series fitted w ith threemethodswas:DHR(7.8%)<FARIMA(12.9%)<SARIMA(13.4%),and MAPE of the halfa-year time series forecasted had the same trend:DHR(3.5%)<FARIMA(5.6%)<SARIMA(6.8%).Other index for forecasting accuracy conveyed the sim ilarmessage.ConclusionA ll threemodels had satisfactory prediction capacity.DHRmodel is superior to FARIMA model and SARIMA modelw ith a higher forecast precision.Themethods and findings in this study may throw light on predicting the incidence of other infectious diseases.
SARIMA model;FARIMA model;DHRmodel;Forecasting;Typhoid fever and Paratyphoid fever
*:国家自然科学基金(81102207);广东省自然科学基金(S2011040005355)
1.南方医科大学公共卫生与热带医学学院生物统计学系(510515)
2.南方医科大学生物医学工程学院数理系
△通信作者:欧春泉,E-mail:ouchunquan@hotmail.com
