量子盘中氢化杂质束缚磁极化子的性质

韩 超，张 策，额尔敦朝鲁

(河北科技师范学院物理系，河北秦皇岛，066004)

随着微纳制造技术的出现和日臻发展，半导体量子点的研究日益为国内外学者所关注，这是因为在量子点结构中，电子、空穴和激子在三维空间受限，呈现具有分立能级的量子态，使得它具有独特的物理特性，如电子结构、输运性质和光学特性等。尤其是，量子点体系作为人工可剪裁的材料，与体材料相比有着显著的非线性光学效应，而且其激发阈值也大大降低，因此量子点体系的光学性质越来越受到人们的重视，已成为当前量子功能器件研究领域中的一个热点。由于大多数人工量子点结构是由离子晶体或极性半导体材料构造，其电子-声子相互作用强烈地影响着它们的物理性质［1］，因此，近年来量子点中极化子的声子平均数的研究受到了学者的极大关注。Zhu等［2］采用Landau-Pekar变分方法研究了量子点中强耦合磁极化子的基态能量和声子平均数。尹辑文等［3］采用线性组合算符和幺正变换方法研究了量子点中强耦合束缚磁极化子声子平均数的温度依赖性。陈时华等［4］采用Pekar类型的变分法研究了非对称抛物限制势作用下的量子点中电子-体纵光学(longitudinal optical，LO)声子强耦合束缚磁极化子的光学声子平均数。张鹏等［5］采用Tokuda改进的线性组合算符法、拉格朗日乘子法和变分法研究了极化子的速率对光学声子平均数的影响。许杰等［6］采用线性组合算符和幺正变换方法研究了库仑场对非对称量子点中强耦合极化子声子平均数的影响。额尔敦朝鲁［7］采用Huybrechts线性组合算符法和Lee-Low-Pines幺正变换法，研究了非对称抛物量子点内弱耦合磁极化子的振动频率和声子平均数的温度依赖性。然而，据目前所知，迄今为止，有关量子点的厚度对氢化杂质束缚磁极化子性质的影响的研究工作尚无报道。随着分子束外延技术和金属有机物化学汽相沉积技术等现代技术和工艺的发展，人们已能制造出几个分子层厚度的准二维量子点［8］。为了简单起见，过去大多数的理论研究都是把量子点当作理想的球形来处理［9，10］，实际上，量子点的形状与生长条件有关，把量子点描述成其他形状如柱形或薄盘也许更为准确［11～13］。笔者采用Lee-Low-Pines变换法和Tokuda改进的线性组合算符法研究外磁场、温度、量子盘的厚度和电子速度对量子盘中氢化杂质束缚磁极化子性质的影响。

1 哈密顿量

假设电子被束缚于氢化杂质中，并与离子晶体或极性半导体中的体纵光学(LO)声子场相互作用。电子在x-y平面内和z方向被不同的限定势限制。杂质原子位于坐标原点(图1)。设外磁场沿z轴方向，矢势用⇀A =B(－y，x，0)/2 描写，则量子盘中电子-LO 声子相互作用体系的哈密顿量为

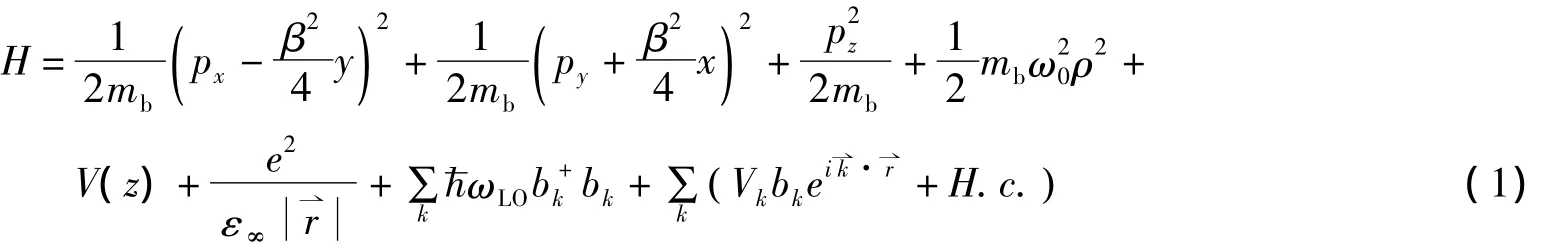
ω0为量子盘的横向受限强度。根据文献［14］和［15］的讨论可知，当z方向的限制比x-y方向的限制大得多的情况下，在z方向仅有最低的电子副带被占据，则z方向与x-y平面没有耦合，那么上述三维问题就可以精确地用一个二维问题来近似;第6项是氢化杂质的库仑势能;第7项是LO声子的哈密顿量，(bk)代表波矢为=(‖，kz)的LO声子的产生(湮灭)算符;最后一项是电子-LO声子相互作用项，式中Vk为相互作用的傅里叶系数

其中，v是晶体的体积，α为电子-LO声子耦合强度，ε∞和ε0分别是高频和静态介电常数。

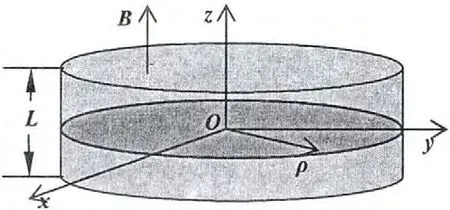
图1 量子盘的结构示意图

2 幺正变换与变分计算

为了讨论量子盘中磁极化子的有效哈密顿量，首先，对电子x-y平面的动量和坐标引入Tokuda改进的线性组合算符［16］

这里

是Lee-Low-Pines幺正变换［17］，其中 fk和为变分参数，A是表征电子-声子耦合强度的物理量，对于本次所研究的电子与 LO 声子强耦合体系，A=0［16，17］。

将式(1)～(5)和(7)～(10)代入(6)式，则可确定变分参量，其中磁极化子的振动频率λ满足

利用这些变分参量还可以得到电子-LO声子体系的声子平均数为

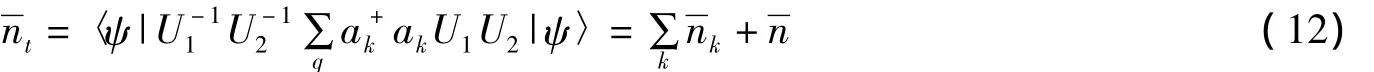
其中

3 结果与讨论

为了直观地了解量子盘中氢化杂质束缚磁极化子振动频率λ和声子平均N数随外磁场的回旋频率ωc，电声子耦合强度α，温度参数γ，电子速率u和量子盘厚度L的变化规律，给出了数值计算结果(图2，图3)。图中各量采用极化子单位(2mb=h=ωLO=1)。

图2 振动频率λ在(a)不同介电常数比η和速度u下随回旋频率ωc，(b)不同耦合强度α和温度参数γ下随量子盘厚度L的变化

图3 平均声子数在(a)不同介电常数比η和速度u下随回旋频率ωc，(b)不同耦合强度α和温度参数γ下随量子盘厚度L的变化

由图2(a)可以看出，振动频率λ随外磁场的回旋频率ωc增加而增大，这表明外磁场将导致电子-晶格的极化场加强，从而加强量子棒中电子-声子-磁场三体相互作用。由图2(a)还可以看出，磁极化子的振动频率λ随介电常数比η的增加而增大，因为介电常数比η增加意味着库仑束缚势增大，这表明因为杂质的存在，使电子和杂质之间存在库仑相互作用，这一库仑场的存在等效于对电子附加另一种约束，致使电子波函数更大的交叠，电子-声子相互作用增强，进而导致磁极化子的振动频率λ随介电常数比η的增加而增大。另外，由图2(a)还可以看出，束缚磁极化子的振动频率λ随电子速率u的增大而增加。这是因为随着磁极化子中电子速率u的增大，致使磁极化子的德布罗意波频率增大。从图2(b)可以看出，磁极化子的振动频率λ随量子盘厚度L的增加而减小，这是因为随着量子盘厚度的增大，电子热运动和电子-声子相互作用因粒子纵向运动空间的增大而减弱，进而磁极化子的能量减小所致，表现了量子盘奇特的量子尺寸效应。从图2(b)也不难看出，束缚磁极化子的振动频率λ随温度参数γ的增加而增大，换句话说，磁极化子的振动频率λ随温度T的增加而减小。这是因为随着温度的升高，声子的热运动加强，致使量子盘中电子-声子相互作用的能量减小，导致磁极化子的振动频率减小。从图2(b)也不难看出，当量子盘厚度L给定时，磁极化子的振动频率λ随耦合强度α的增加而增大，这是因为耦合强度α越大，意味着电子-声子相互作用越强，进而导致磁极化子振动频率的增大。

4 结 论

基于Lee-Low-Pines变换法和Tokuda改进的线性组合算符法研究了量子盘中氢化杂质束缚磁极化子振动频率和声子平均数的磁场和温度依赖性。结果表明，(1)磁极化子的振动频率λ随电子-声子耦合强度α，介电常数比η，电子的速率u和外磁场回旋频率ωc的增加而增大，随温度T的升高和量子盘厚度L的增加而减小。(2)磁极化子的声子平均数随电子-声子耦合强度α，介电常数比η和外磁场回旋频率ωc的增加而增大，随温度T的升高、电子的速率u的增加而减小，随量子盘厚度L的增加而振荡减小。

［1］ Fai LCI，Teboul V，Monteil A，etal.Polaron in a quasi1D cylindrical quantum wire［J］.Condensed Matter Physics，2005，8(3):639-650.

［2］ Zhu K D，Kobayashi T.Magnetic field effects on strong-coupling polaron in quantum dots［J］.Phys Lett A，1994，190(3-4):337-340.

［3］ 尹辑文，于毅夫，肖景林.抛物量子点中强耦合束缚磁极化子的温度效应［J］.半导体学报，2006，27(12):2 123-2 126.

［4］ 陈时华，肖景林.非对称抛物限制势量子点中强耦合束缚磁极化子的性质［J］.半导体学报，2006，27(11):1 923-1 926.

［5］ 张鹏，肖景林.量子点中极化子的速率对光学声子平均数的影响［J］.中国石油大学学报:自然科学版，2007，31(6):127-129，134.

［6］ 许杰，肖景林.库仑场对非对称量子点中强耦合极化子声子平均数的影响［J］.发光学报，2008，29(3):547-550.

［7］ 额尔敦朝鲁，张鹏，辛伟.非对称量子点中磁极化子声子平均数的温度特性［J］.中国石油大学学报:自然科学版，2009，33(4):171-174.

［8］ Fafard S，Leonard D，Merz JL，et al.Electron and hole energy levels in InAs self assembled quantum dots［J］.Appl Phys Lett，1995，66:1 767-1 769.

［9］ Jacak L，Hawrycak P，Wjs A.Quantum Dots［M］.Berlin:Spring-verleg，Heidelberg，1998.

［10］ Borrelli N F，Hall DW，Holland H J，et al.Quantum confinement effects of semiconductingmicrocrystallites in glass［J］.JAppl Phys，1987，61:5 399-5 409.

［11］ Kash K，Scherer A，Worlock JM，et al.Optical spectroscopy of ultrasmall structures etched form quantum wells［J］.Appl Phys Lett，1986，49:1 043-1 045.

［12］ Reed MA，Randall JN，Aggarwal R J，et al.Observation of discrete electronic states in a zero-dimensional semiconductor nanostructure［J］.Phys Rev Lett，1988，60:535-537.

［13］ Chen C Y，LiW S，Teng X Y，et al.Polaron in a quantum disk［J］.Physica B，1998，245:92-102.

［14］ Peeters FM，Schweigert V A.Two-electron quantum disks［J］.Phys Rev B，1996，53(3):1 468-1 474.

［15］ Price R，Zhu X，Sarma SD，Platzman PM.Laughlin-liquid-Wigner-solid transition at high density in wide quantum wells［J］.Phys Rev B，1995，51(3):2 017-2 021.

［16］ Tokuda N.A variational approach to the polaron problem［J］.JPhys C:Solid State Phys，1980，13:L851-L855.

［17］ Lee T D，Low FM，Pines D.Themotion of slow electrons in a crystal［J］.Phys Rev，1953，90:297-302.

［18］ 白旭芳，乌云其木格，辛伟，等.Rashba自旋-轨道相互作用影响下量子盘中强耦合磁极化子性质的研究［J］.物理学报，2014，63(17):177 803.