量子点中双极化子和磁双极化子的研究进展

额尔敦朝鲁，董伟伟，张 聪

(河北科技师范学院物理系，河北秦皇岛，066004)

随着分子束外延、金属有机化合物气相沉积等技术的发展，人们已能制造出准零维纳米结构的量子点。在这样的纳米结构中，由于量子点限定势的存在限制了电子的运动，不仅呈现具有分立能级的量子态，而且电子与晶格间相互作用对电子的能级结构产生影响，研究这一影响所产生的效应，即极化子效应，具有十分重要的现实意义，现已有不少学者［1～5］研究了极化子对量子点的影响。然而，不难看出，近年来人们对量子点结构中极化子的研究大多都局限于单个电子与体纵光学(longitudinal optical，LO)声子相互作用形成的单极化子情形，而量子点中双极化子的问题却未受到人们的广泛关注。研究表明［6］，2个等同的带电载流子，如电子或空穴，在固体中通过屏蔽的库仑势相互排斥，在大多数情况下不能形成束缚态，然而带电载流子的性质可由它们与振动的晶格相互作用，即电声相互作用而改变。在有些材料中，如离子晶体或极性半导体，这个电声耦合作用足够大能克服库仑排斥而建立一个稳定的电子对或空穴对，因为它包括2个带电的极化子，所以称为双极化子，在固体中双极化子能否形成决定于电子(空穴)的排斥及它们与畸变晶格的吸引二者之间的竞争。“双极化子”一词首先是由Pekar［7］引入的，继后，许多学者［8～12］对它的物理性质进行了广泛的研究。本研究综述了近几年来人们对抛物线性限制势量子点中双极化子［13，14，17］和磁双极化子［19］性质方面的部分研究工作。

1 抛物量子点中强耦合双极化子的有效势

量子点中2个电子－LO声子相互作用的系统由下面的Frölich哈密顿量描述

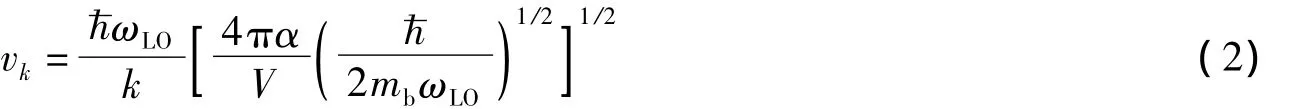
其中，V晶体的体积，α是无量纲的电子-声子耦合

其中，ε∞(ε0)是高频(静态)介电常数，称为单极化子的半径。为了计算方便，引进双电子的质心坐标)/2和相对坐标，得到

首先，对双极化子的质心坐标和动量引入Huybrechts线性组合算符［15］

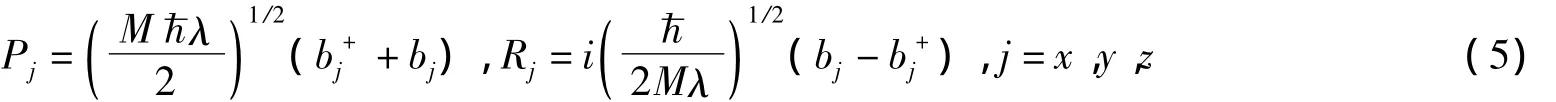
其中，λ为变分参数，它表示双极化子质心的振动频率，j=x，y，z。再对哈密顿量H作Lee－Low－Pines(LLP)幺正变换［16］，

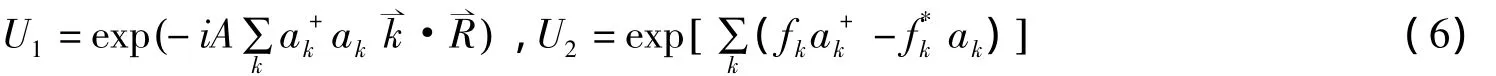
其中，fk和为变分参数，A是表征电子-声子耦合强度的物理量，对于笔者所研究的电子与LO声子强耦合体系，A=0［15，16］。推得变分函数

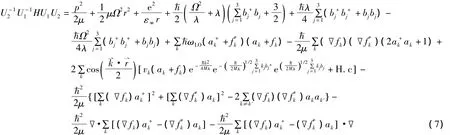
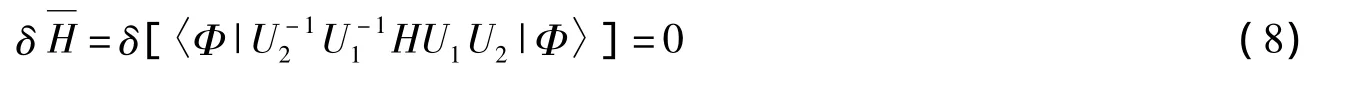
这里

是零温(0 K)下体系的尝试波函数，其中ψ(r)为双极化子相对运动的波函数，|0〉a和|0〉b分别描写双极化子质心运动和LO声子的真空态，满足ak|0〉a=bj|0〉b=0。对 fk，和λ的变分极值给出双极化基态能量的上限，

其中，F(fk，，λ)为变分函数，它对参数 fk，和λ的变分极值Heff称为电子-声子系统的有效哈密顿量，经计算可得

式中

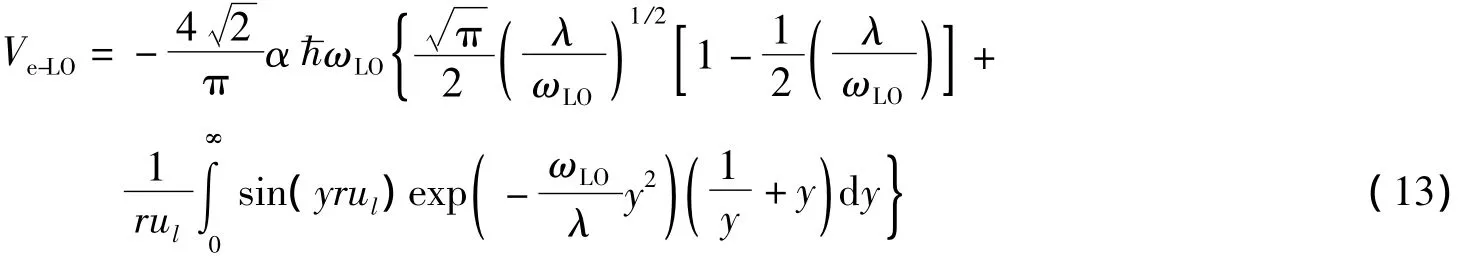
是描写电子-声子相互作用的特征函数，称为诱生势。双极化子质心的振动频率λ满足:

在以上推导中忽略了多声子之间相互作用引起的小项和波矢高阶小项的贡献。不难看出，双极化子有效势Veff由库仑势Vcoul，限定势Vconf和诱生势Ve－LO等三部分组成;数值计算结果表明，双极化子的振动频率λ、诱生势的绝对值|Ve－LO|和有效势的绝对值|Veff|均随电子-声子耦合强度α的增加而增大，随电子间相对距离r的减小而增大;耦合强度α和电子间相对距离r是影响有效势的主要因素，而量子点半径R0和介电常数比η对有效势Veff的影响较小。

2 量子点中强耦合双极化子的声子平均数与有效质量

首先，用下列Tokuda改进的线性组合算符［18］代替Huybrechts线性组合算符(5)式

这里

是有限温度下体系的尝试波函数，|nk〉为声子态，|nj〉为极化子态。〉按照量子统计，将电子数n和声子数以其平均数代替。

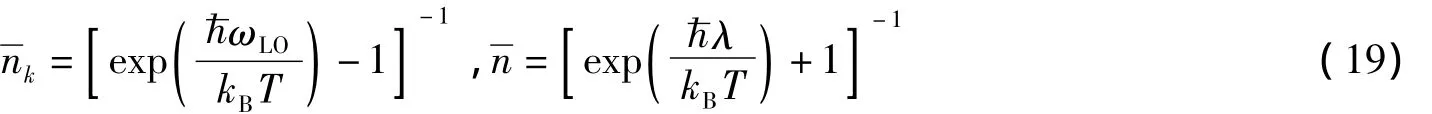
将式(15)，(17)～(19)代入(16)式，可得

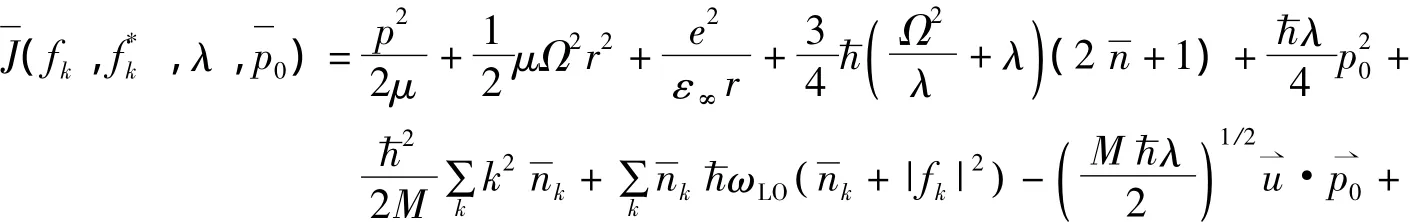
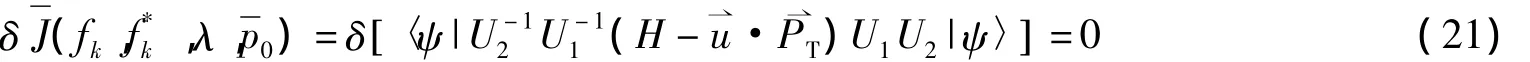
则可确定变分参量λ，fk和，利用这些变分参量还可以得到电子－LO声子体系的声子平均数:

其中

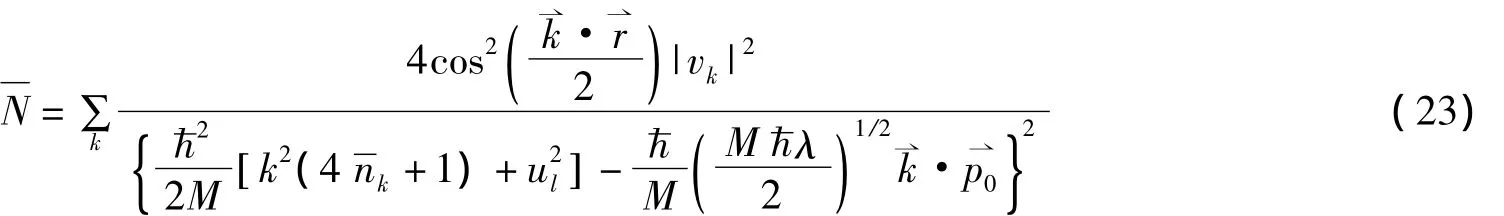
是双极化子的LO声子平均数。利用这些变分参量还可算得体系的总动量的平均值

其中

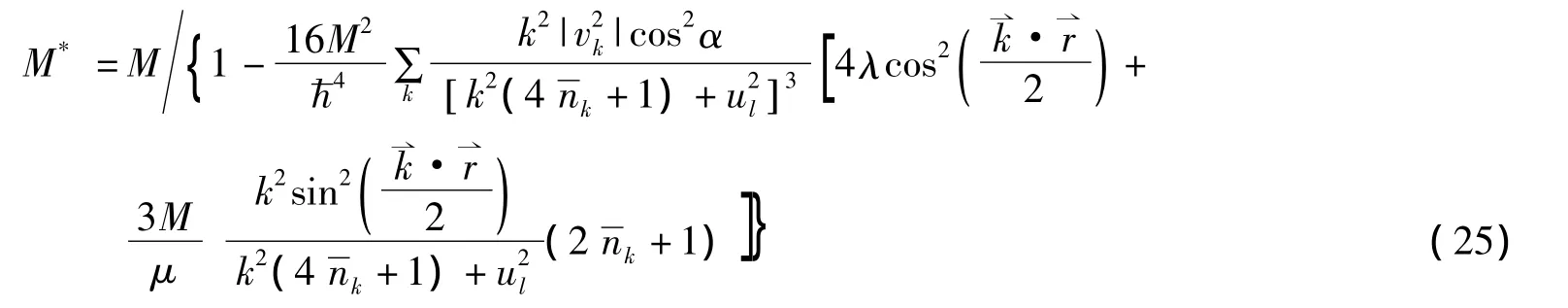
3 量子点中磁双极化子的自旋极化态性质

考虑被约束在一个二维(x－y平面)抛物势量子点中与LO相互作用的两电子体系，设外磁场沿z轴方向，则体系的 Frölich 哈密顿量为［19］

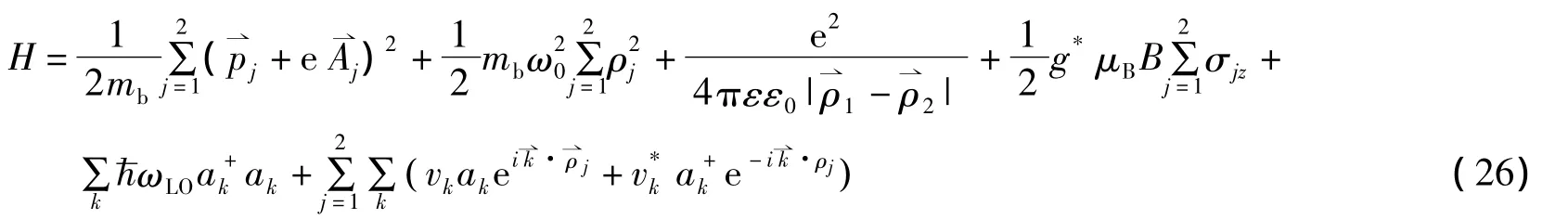
式中，前2项表示两电子的单粒子能量(其中第2项表示量子点的限定势)，第3项表示两电子间库伦相互作用能，第4项表示电子自旋与外磁场相互作用能，第5项表示局域LO声子场的能量，最后一项表示电子－LO声子耦合项。Aj=B(－yj，xj，0)/2(j=1，2)是在电子处的矢势，和(j=1，2)分别是电子在平面上的动量和矢量坐标，=(σx，σy，σz)是 Pauli算符，μB是玻尔磁子，ε是电子运动所处介质的相对介电常数，ω0为电子所受量子点约束势强度，g*是朗德因子。

的极值问题，这里

是LLP幺正变换，其中，fk和为变分参数，对于笔者所研究的电子与LO声子强耦合体系，A1=A2=0，假设对于体系的基态和第一激发态，高斯函数近似成立，则依据Pekar类型的变分法［20］，体系的尝试波函数|ψ〉可以选为

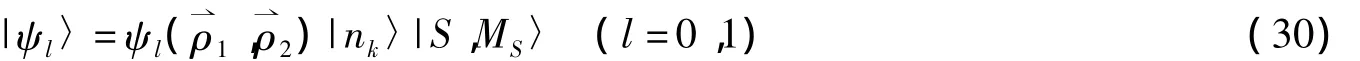
其中，F(－n，|m|+1，λ2ρ2/2)是河流超几何函数，N为归一化系数，λ为变分参数。对于体系的基态);第一激发态:ψ1);|nk〉是声子态;|S，MS〉是两电子体系的自旋波函数［21］，S=0，1为总自旋量子数，Ms=－S，－S+1，…，S为总自旋磁量子数。

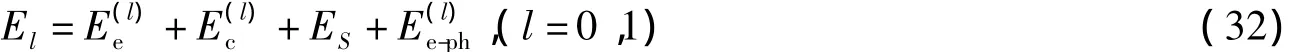
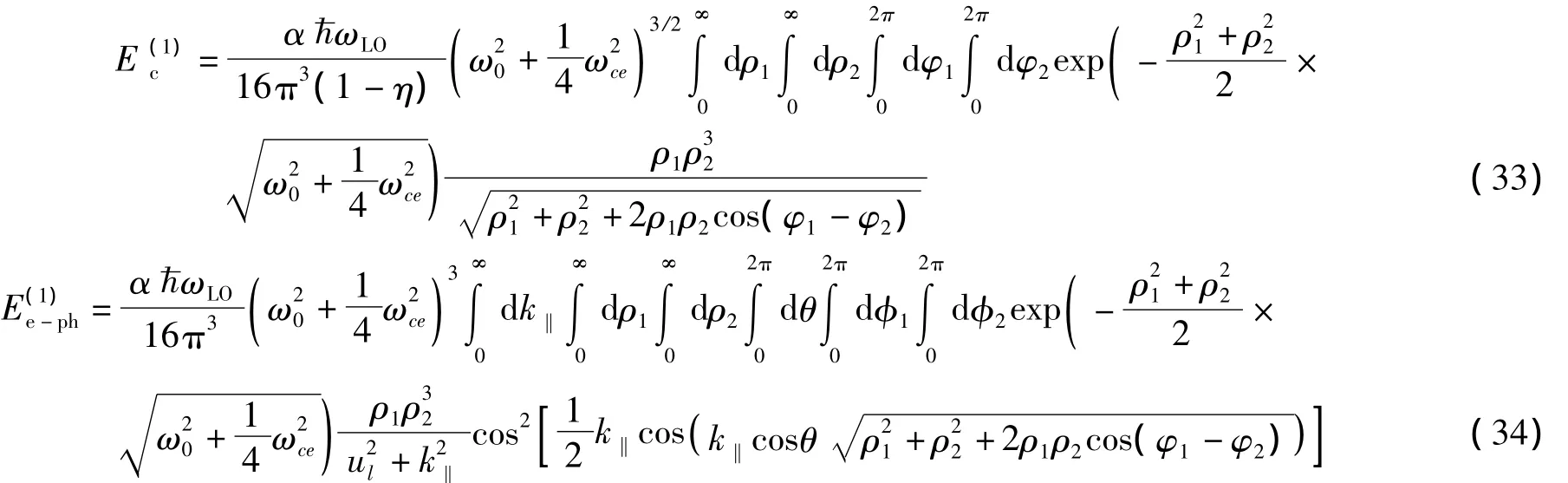
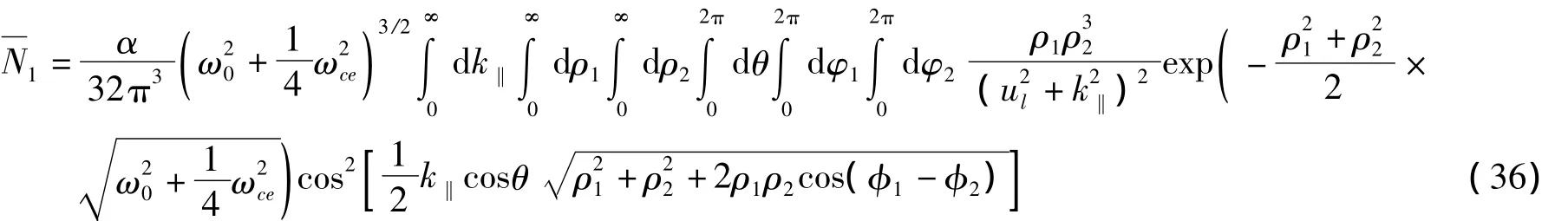
由(32)式可以看出，磁双极化子的基态能量E0和第一激发态能量E1由单粒子能量Ee、两电子间库伦相互作用能Ec、电子自旋与磁场相互作用能Es和电子-声子相互作用能Ee－ph等4部分组成。数值结果表明，单粒子“轨道”运动与磁场相互作用导致了第一激发态能级E1分裂为和，而电子自旋-磁场相互作用的效应又使基态和第一激发态的各能级均产生了3条“精细结构”;磁双极化子的基态声子平均数和第一激发态声子平均数N1随量子点受限强度ω0，电子-声子耦合强度α和磁场的回旋共振频率ωc的增加而增大;而Ee－ph的取值总是小于0，其绝对值随α，ω0和ωc增加而增大;电子-声子相互作用的效应是束缚态磁双极化子形成的有力因素;而限定势和电子之间的库仑排斥能的存在不利于束缚态磁双极化子的形成;能量为的磁双极化子要比能量为的磁双极化子更容易且更稳定的处于束缚态。

4 展 望

近年来，双极化子的理论研究和实验研究在有机聚合物领域进展较多，但在极性晶体或极性半导体中双极化子的实验研究甚少，一定程度上影响着双极化子理论工作的进展;另外，双极化子的Rashba效应的研究仍为空白;双极化子的自旋单态和三重态效应有待深入研究。

［1］ Huangfu Y F，Yan ZW.Bound polaron in a spherical quantum dot under an electric field［J］.Physica E，2008，40(9):2 982－2 987.

［2］ Chen SH，Yao Q Z.The effectivemass of strong－couplingmagnetopolarons in a parabolic quantum dot［J］.Modern Physics Letters B，2011，25(32):2 419－2 425.

［3］ Li Z X，Xiao J L，Wang H Y.The effective mass of strong－coupled polaron in an asymmetric quantum dot induced with rashba effect［J］.Modern Physics Letters B，2010，24(23):2 423 －2 430.

［4］ Xiao W，Xiao JL.The effectivemass of strong－couplingmagnetopolaron in quantum dot［J］.Int JMod Phys B，2007，21(12):2 007－2 016.

［5］ Eerdunchaolu，Xin W，Zhao YW.Influence of lattice vibration on the ground－state ofmagnetopolaron in a parabolic quantum dot［J］.Modern Physics Letters B，2010，24(27):2 705－2 712.

［6］ Adamowski J.Formation of a Frohlich bipolarons［J］.Phys Rev B，1989，39:3 649－3 652.

［7］ Pekar S I.Research on electron theory of crystals［M］.Publisher:USABC，Washington D C，1963 .

［8］ Pokatilov E P，Crotitoru MD，Fomin V M，et al.Bipolaron stability in an ellipsoidal potentialwell［J］.Phys Stat Sol(b)，2003，237:244－251.

［9］ Senger R T，Ercelebi A R T.On the stability of Fröhlich bipolarons in spherical quantum dots［J］.JPhys:Condens Matt，2002，14:5 549－5 560.

［10］ Ruan Y H，Chen Q H，Jiao Z K.Variational Path－integral study on a bipolaron in a parabolic quantum wire orwell［J］.Internat JModern Phys B，2003，17:4 332－4 337.

［11］ Hohenadler M，Littlewood P B.Quantum Monte Carlo results for bipolaron stability in quantum dots［J］.Phys Rev B，2007，76:155 122－155 126.

［12］ Fai L C，Fomethe A，Fotue A J，et al.Bipolaron in a quasi－0D quantum dot［J］.Superlatt Microstuct，2008，43:44－52.

［13］ Eerdunchaolu，Wei Xin.Temperature dependence of the properties of strong－coupling bipolraon in a quantum dot［J］.Physica B，2011，406:358－362.

［14］ Xiao J L.Properties of a strong coupling bipolaron in an asymmetric quantum dot［J］.JLow Temp Phys，2014，174:284－291.

［15］ Huybrechts J.Note on the ground－state energy of the Feynman polaron［J］.JPhys C:Solid State Phys，1976，9(8):211－212.

［16］ Lee T D，Low FM，Pines D.Themotion of slow electrons in a crystal［J］.Phys Rev，1953，90(1):297－302.

［17］ Xin W，Gao ZM，Wuyunqimuge，et al.Influence of temperature and LO phonon effects on the effective mass of quasi0D bipolarons in the strong－coupling limit［J］.Superlattices and Microstructures，2012，52:872－879.

［18］ Tokuda N.A variational approach to the polaron problem［J］.JPhys C:Solid State Phys，1980，13:L851－L855.

［19］ Eerdunchaolu，Han C，Xin W，et al.Influence of magnetic field and lo phonon effects on the spin polarization state energy of strong－coupling bipolaron in a quantum dot［J］.JLow Temp Phys，2014，174:301－310.

［20］ Chatterjee A.Strong－coupling theory for the multidimensional free optical magneto polar on［J］.Phys Rev B，1990，41:1 668－1 670.

［21］ Schiff L.Quantum Mechanics(3nded)［M］.New York:McGraw－Hill，Inc，1968.