内压和弯矩联合作用下理想弯头的有限元分析
2014-03-09李晓红
张 鹏,李晓红
(西安石油大学机械工程学院,西安 710065)
0 前言
管道系统由于受到不同工况的影响,在不同地貌或是特殊地方需要改变管线方向,而弯头就是实现这一方案的主要管线部件。在管道系统中弯头不仅可以改变介质的流向,还可以通过自身的柔性吸收管道热位移并减小管道的推力[1]。与普通直管相比,弯头结构更加复杂。当弯头受到轴向拉力、弯矩和内压作用时,最大应力往往出现在弯头处,因此弯头往往会成为管线系统的薄弱环节[2-4],所以对于弯头在受拉伸、弯矩、内压作用下的应力分析是十分必要的。
本研究主要考虑弯矩对内压弯头的影响,由于轴向拉力对弯头的影响主要是由于拉力对弯头各截面产生弯矩的作用从而改变各截面的应力。因此分别从单独内压,单独轴向拉力,轴向拉力与集中弯矩,内压与集中弯矩,内压与轴向拉力以及内压、集中弯矩和轴向拉力共同作用的6种载荷情况进行分析。
1 模型建立
1.1 基本假设
为简化模型,先做如下假设:①弯头为理想弯头,无制造缺陷存在,制作符合规范,即不考虑加工残余应力的影响;②材料服从各向同性假设;③小变形假设,不考虑弯头端面的变形[5]。
1.2 材料模型
随着石油行业的发展,油气运输管材更趋近于高韧性、屈服极限大的材料。因此本研究选用X100钢级弯头进行分析。该材料弹性模量E=207 GPa,屈服强度ReL=733 MPa,泊松比v=0.3,抗拉强度Rm=778 MPa[6]。
1.3 几何模型
弯头大都与直管段焊接,直管对弯头有一定的加强作用,当弯头连接的直管段长度大于管径的3倍时,直管对弯头的影响趋于稳定,此时可以消除端部效应[7]。本研究选取弯头模型如图1所示,弯头工作尺寸为:公称直径DN=100 mm,外径D=114.2 mm,壁厚t=13 mm,弯头曲率半径R=152 mm,设计压力p=20 MPa,弯头接直管段长度L=360 mm。
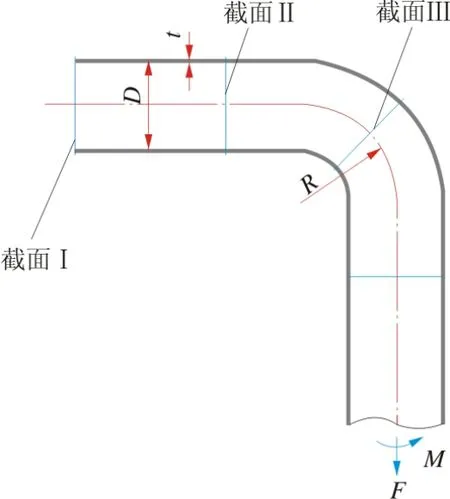
图1 弯头模型示意图
1.4 有限元模型的建立
研究时,不考虑温度变化的影响,在结构屈服时,服从Von Mises屈服准则。由于弯头的不规则形状,进行有限元分析时,为防止因为结构的外形影响而降低分析的精确度,采用Solid95单元[8]。建模过程中,考虑到弯头结构的特殊性,采用弯头完整模型进行分析。在模型划分网格时由于弯头比直管段的结构复杂,而且为了提高计算精度,直管段网格大小取10 mm,弯头处网格大小取5 mm。弯头有限元模型如图2所示。

图2 弯头有限元模型
1.5 载荷加载及边界条件
管线处于试压阶段时,管道及弯头受到内压作用;实际工作时,管道受到输送介质的重力及管道自身重力作用产生弯矩。在工作时若输送介质波动较大或者遇到外部激振时,由于弯头直管段的震动和固定就可能产生扭转作用,因此主要研究内压(p)、轴向拉力(F轴)、面弯矩(M)对弯头的应力影响。弯头不同工况时载荷分析见表1。
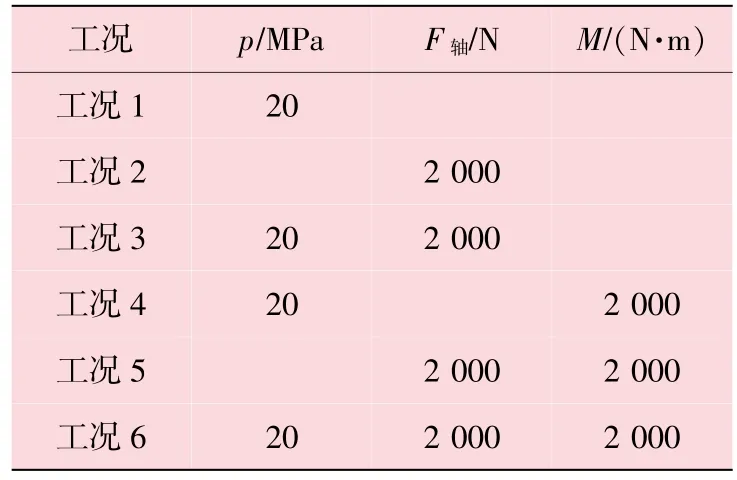
表1 弯头6种工况载荷
由于在管道管壁上受拉力作用,因此对于轴向拉力加载时将集中力需等效为作用于管道横截面上的均布载荷,而弯矩加载时将作用点与管道截面耦合为一个刚性整体[9-10],这样就可以保证分析计算的结果更趋近于真实的管道应力状态。由于弯头焊接在直管段上,因此分析弯头受力时,采取截面Ⅰ(截面位置见图1)固定,另一端直管自由,在自由端施加各种载荷[11-12]。
2 弯管应力分析
利用ANSYS有限元分析软件,对表1中6种工况进行弯头的有限元应力分析,对最复杂的工况6的应力云图从弯头整体、截面Ⅰ、截面Ⅱ、截面Ⅲ进行分析,如图3所示。
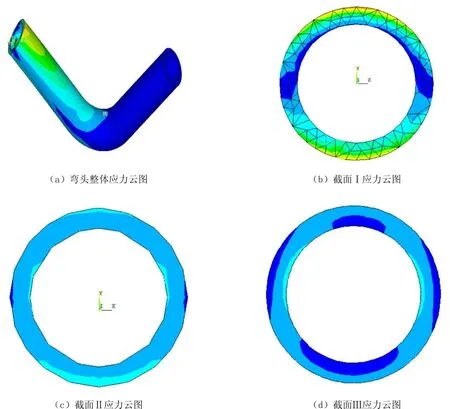
图3 工况6应力分析结果
从图3可以看出,在工况6的载荷状况下,弯头整体的应力最大处出现在弯头所接直管段固定端外侧。通过检测,弯头所接直管段固定端外侧最大应力值为754 MPa;截面Ⅱ弯头与直管焊接处最大应力约为279 MPa;截面Ⅲ(弯头中心截面)的最大应力约为186 MPa。分析认为,在此6种外载荷工况中,由于轴向力对弯头的作用主要是以弯矩的影响表现出来,且弯头改变了管线的几何方向,所以作用在圆管上的力可以看作是剪应力对悬臂梁的作用。其应力可以通过多向应力公式[13]计算得出,
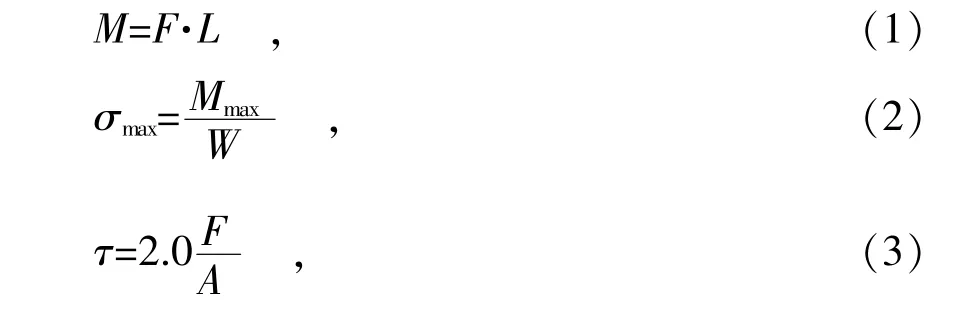
式中:M-剪力产生的弯矩;
F-剪力;
L-受影响截面到剪力作用点的距离;
σmax-弯曲最大正应力;
利用多向应力的计算,可以计算出弯头的最大应力点,见表2。可以看出,在有轴向力和面弯矩作用时最大应力状态点出现在固定端端面上。
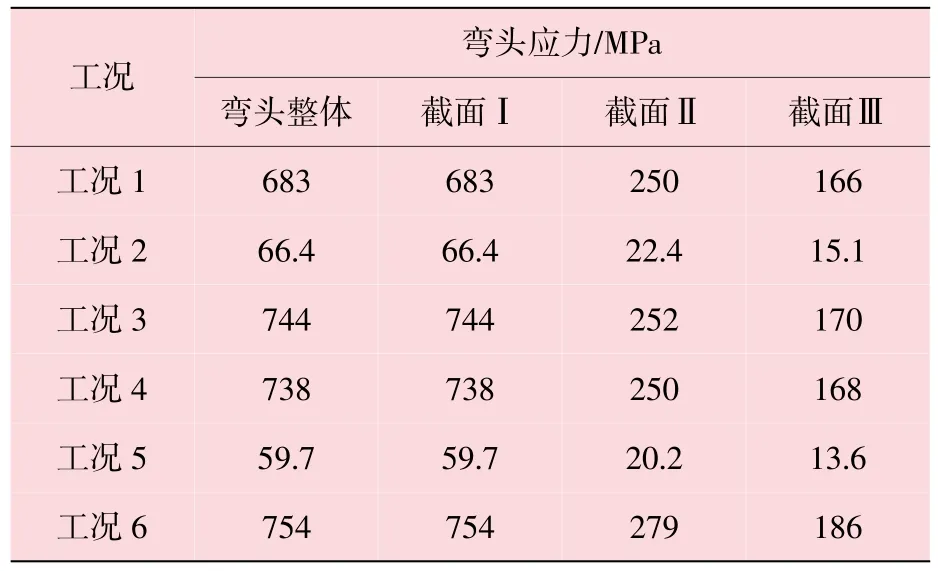
表2 6种工况下弯头的应力值
将表2的分析数据绘制为弯头的应力折线图,如图4所示。
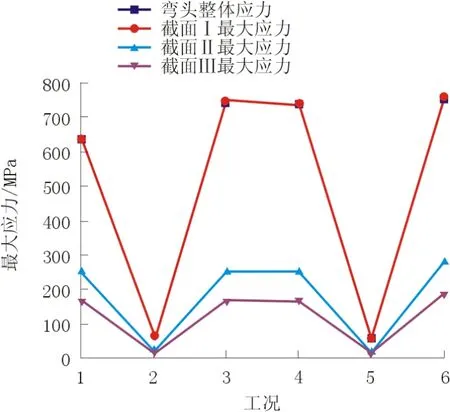
图4 6种工况中弯头各截面的应力对比
分析表2中的应力数据及图4中的折线图可知:
(1)比较工况1和工况2可以知道,对于工作中的弯头,应力主要是由内压产生。
(2)比较工况3、工况4和工况5弯头的整体应力值,对于有无内压作用弯头整体的应力值变化较大。而且弯头面弯矩和轴向力的作用影响不大。工况3和工况4的应力值基本一致,没有过大的变化。
(3)比较6种工况弯头的最大应力值,与弯头整体最大应力曲线与截面Ⅰ最大应力曲线,在6种工况中最大应力点均出现在弯头所接直管段的上边缘处。
(4)比较工况1、工况3和工况4与截面Ⅰ,截面Ⅱ,截面Ⅲ最大应力曲线可以看出,轴向力与面弯矩对于最大应力值影响较大,但是对截面Ⅱ和截面Ⅲ的最大应力值影响不大。
3 结 论
以DN100,SCH160理想90°弯头为例,分析了内压、轴向力及面弯矩联合作用下弯头的应力分布,得出结论如下:
(1)轴向力对于弯头的影响主要是通过弯矩的形式表现出来的;
(2)面弯矩和轴向力对弯头应力的影响基本相似,它们主要对弯头所接直管段的固定端处最大应力影响比较明显,对于其他各截面的应力值影响不大;
(3)内压、面弯矩、轴向力联合作用下比单独载荷作用对弯头的影响大,内压和弯矩联合作用时,弯头中心处和固定端直管处易出现应力集中,弯头中心处应力集中主要由内压控制,而固定端直管的应力集中主要由联合作用载荷控制;
(4)虽然弯头的结构比直管复杂,在各种工况下都会在弯头中心处出现应力集中的现象,但是由于直管上的约束影响,最终弯头最大应力处并不是在弯头中心处,而会出现在约束端。
[1]雷俊杰,王瑞英,王学翠,等.基于有限元的外载作用下弯头局部强度分析[J].辽宁化工,2013,42(05):506-509.
[2]段志祥,沈士明.内压作用下弯管塑性极限载荷分析与实验研究[J].压力容器,2004,21(08):1-4.
[3]段志祥,沈士明.内压与弯矩联合作用下局部减薄弯管的塑性极限载荷[J].核动力工程,2007,28(06):87-91.
[4]孙兰萍,赵建平.不等厚性对弯头应力分布影响的有限元研究[J].南京工业大学学报,2006,28(03):49-52.
[5]刘波.弯头极限载荷研究概述[J].化工设备与管道,2012,49(05):64-66.
[6]王钟羡,黄建业.X100管线钢裂纹体的弹塑性断裂失效分析[J].江苏大学学报,2011(32):175-178.
[7]徐思浩.90°弯头的应力分布[J].化工设备与管道,2001,38(04):38-39.
[8]黄鉴,马业华.燃气管道弯头应力分布及塑性极限载荷分析[J].煤气与热力,2012(32):B01-B03.
[9]尚晓江,邱枫,赵海峰.Ansys结构有限元高级分析方法与范例应用[M].北京:中国水利水电出版社,2008:68-73.
[10]余伟炜,高炳军.Ansys在机械与化工设备中的应用[M].北京:中国水利水电出版社,2007:114-183.
[11]王辰,秦宜奋,张宏宇,等.面内开/闭弯载荷作用下压力管道弯头的塑性研究[J].压力容器,2006,23(04):7-12.
[12]刘波.无缺陷90°弯头应力状态的有限元分析[J].中国石油和化工标准与质量,2007(06):69-103.
[13]刘鸿文.材料力学[M].北京:高等教育出版社,2004:138-155.
