X80钢CTOD有限元计算及断裂韧度评估
2014-03-09叶运勤苗张木
叶运勤,苗张木
(武汉理工大学 交通学院,武汉430063)
0 前 言
钢材断裂韧性不足会导致钢结构脆断,其危害性非常大,前期难以监控,一旦发生就会迅速造成结构某部位甚至整体失效,无法采取有效的措施进行制止。因此,对于钢结构关键部位材料断裂韧性的评估尤为重要。
管线钢的断裂韧性评定常规采用夏比冲击(CVN)试验。然而随着管线钢级的提高,工作环境的改变,CVN试验值已不能满足作为质量验收和韧性评价标准的要求。其试验环境与管道运行过程中的实际状况相差太大,测出的试验值不能真实反映管线钢的抗开裂能力。而CTOD(裂纹尖端张开位移,crack tip opening displacement),作为一个重要的弹塑性断裂参量,因其直观性与易测性,正在逐步被研究者广泛采纳,成为评定管线钢断裂韧性的重要准则之一[1]。
Wells首先提出弹塑性条件下的CTOD断裂判据

式(1)中δ是指裂纹体受载后,处于原裂纹尖端、垂直于裂纹方向的裂纹尖端张开位移。式(1)说明当裂纹尖端张开位移δ达到某一临界值δc时,裂纹将会开裂,δc即为材料断裂韧度。
本研究将用有限元计算裂纹体受载后,在原裂纹尖端垂直于裂纹方向的裂纹尖端张开位移(即δ),并对有限元计算结果的精确性进行验证,然后按照BS 7448规范检测材料的δc(以下称CTOD试验),按照公式(1)即可对受力钢结构的关于断裂韧度进行评估,公式(1)成立,则结构安全。
1 有限元方法计算裂纹尖端张开位移δ
以X80钢薄板存在含中心I型穿透性裂纹为例(如图1所示),裂纹长为2a,在“无限远”处有双向均匀拉应力σ,令a=2 mm,板宽W=80 mm,板长L=100 mm,板厚10 mm,弹性模量E=2×105MPa,屈服应力σs=645 MPa,本研究将利用有限元计算在外力作用下裂纹尖端张开位移δ的大小,分别用K-δ方法和COD-δ方法计算外力作用下裂纹尖端张开位移δ。
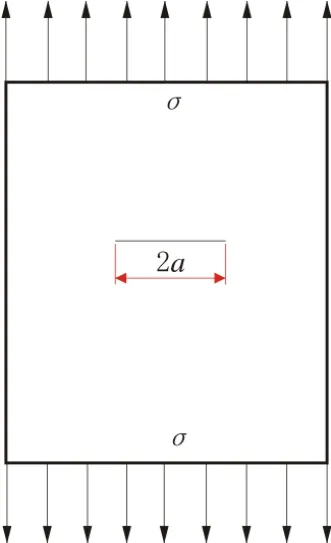
图1 含裂纹体力学模型
1.1 K-δ方法
K-δ方法要先利用有限元计算应力强度因子K,然后根据小范围屈服条件下K与δ的函数关系,推算出δ。K与δ关系为

其中,应力强度因子KI的有限元计算过程为[2]:因裂纹尖端的应力和应变具有高梯度性质,实际上具有奇异性,Kscon命令构造2D奇异单元利用命令PATH和PPATH定义裂纹面及其路径,最后利用命令可以采用KCALC计算应力强度因子,Kscon命令和KCALC命令只能用于2D模型。
根据以上阐述的计算应力强度因子的有限元方法,采用平面单元PLANE82,采用1/4对称模型,用Kscon命令生成奇异单元,划分网格后如图2所示。
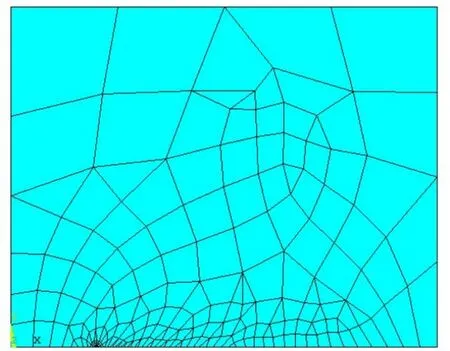
图2 1/4模型划分网格
施加边界条件后,经过有限元计算,得KI=25.5 MN/m3/2,根据式(2)在ANSYS中利用APDL语言输入KI积分与δ的关系语句,即可得出δ,计算得出δ=0.050 mm。
1.2 COD-δ方法
CTOD(即δ)的定义目前存在不同意见,如δ5法[3]:加载前,以原始裂纹尖端为中点,垂直于裂纹扩展方向做1条5 mm的线段,并于线段两端点做标记点;试验加载后,裂纹尖端发生扩展,两标记点之间的距离有所增大,增大的量从一定程度上反映出裂纹尖端张开位移的变化,可以定义CTOD。又如在工程应用中,往往采用另一种方法定义CTOD,如图3所示[4]。当裂纹尖端受到荷载后逐渐张开,裂纹尖端发生钝化。钝化区的材料产生塑性变形,在垂直于荷载的方向上发生收缩而形成伸长区高度,这便是CTOD(δ)。
由于CTOD的定义目前存在不同意见,COD-δ方法可以定义为先利用有限元计算沿裂纹长度方向某处COD,然后利用COD与δ的函数关系计算δ。根据COD的定义,可取距离裂纹尖端很近的某节点在外力作用下的竖向位移,然后乘以2作为该处的COD,COD与δ的关系如图4所示。
COD与δ的函数关系为
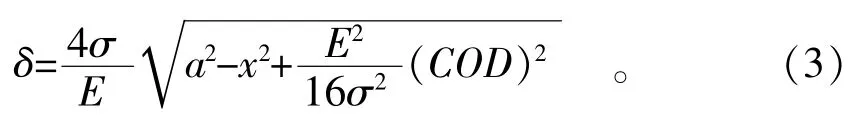
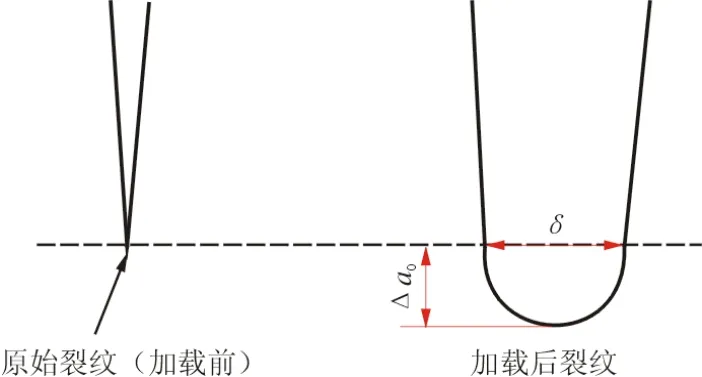
图3 CTOD原始裂纹尖端定义
图4 COD与δ关系图
当x的取值尽量接近a时,即尽量接近裂纹尖端时,计算δ产生的误差小[5]。本研究取x=1.97 mm,即距离裂纹尖端距离为0.05 mm。经有限元计算,得x=1.97 mm处的COD=0.050 mm,然后利用公式(3)[5],在ANSYS中利用APDL语言输入KI积分与δ的关系语句,即可以得出δ=0.051 mm。
1.3 J-δ方法
J-δ方法通过利用有限元计算J积分,然后根据小范围屈服内J积分与δ的关系,在ANSYS中利用APDL语言输入J积分与δ的关系语句,最终得出δ。J积分与δ的关系为

式中:m为CTOD减小因子,取值范围为1~2[6],塑性区较小时m取1[7]。
J积分计算过程:ANSYS11.0之前的版本需要编制宏程序,过程繁琐,不易实现,新的版本增加了CINT命令,可以直接求解J积分[2]。根据CINT命令得力学模型的J=0.032 3 MN/m,则根据J-δ方法计算得的δ的取值范围为0.050 mm。
1.4 有限元方法计算准确性的理论验证
根据断裂力学知识,在线弹性或者小范围屈服时,对于无限大板含中心裂纹的平面应力模型,应力强度因子KI和裂纹尖端张开位移δ的公式分别为
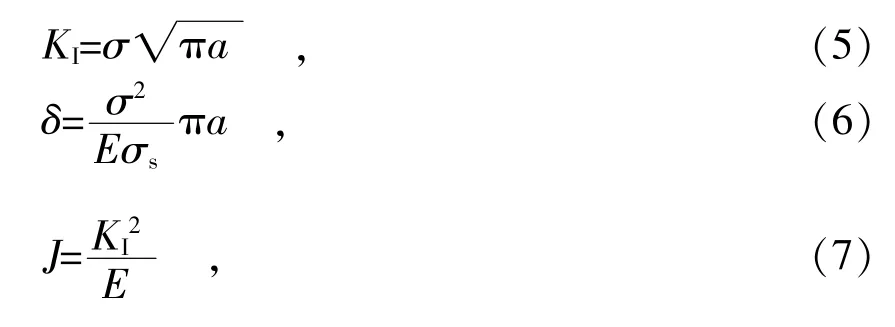
代入 σ=10 MPa, a=2 mm, σs=700 MPa, E=2×105MPa,得出 KI=25.06 MN/m3/2, δ=0.049 mm, J=0.031 3 MN/m。有限元计算与断裂力学理论计算对比见表1。
因此,采用有限元计算KI,J,δ是有效的。
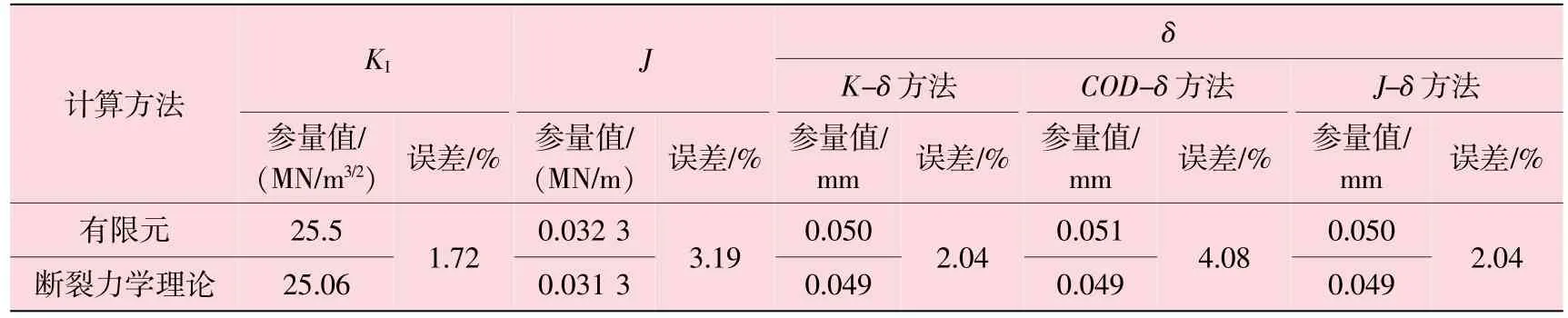
表1 有限元计算与断裂力学理论计算对比
2 CTOD试验测试材料的δc值
2.1 CTOD试验原理
图5是CTOD试验原理示意图。CTOD试验的试样往往采用三点弯曲的加载方式,为试样的正视图,其中点A为原始裂纹的尖端点。三点弯曲荷载会使试样裂纹尖端发生变形,该变形是弹性的,随着荷载水平的增大,裂纹尖端材料达到弹性极限,弹性变形进而发展为塑性变形。随着塑性变形程度的增加,裂纹尖端两侧的裂纹面会绕着裂纹尖端下方的某一点O作方向相反的刚体转动,裂纹尖端随即发生钝化,原始裂纹尖端张开一定的位移,记为δ。
图5中,W表示试样的宽度;a表示初始裂纹的长度;(W-a)表示三点弯曲荷载下的韧带宽度;图中V两侧的刀口用来安装夹伸引伸计以测定刀口间张开位移;刀口用厚度为z的薄板加工而成。Vp表示夹伸引伸计记录的裂纹口张开位移中的塑性位移,与之相对的裂纹尖端张开位移的塑性部分为δp;rp表示塑性变形阶段的旋转因子,它的意义是试样塑性变形时的旋转中心O到原始裂纹尖端的距离与韧带宽度(W-a)的比值。不同的规范标准对rp的取值存在着一些差异,BS 7448系列标准[8]建议取rp=0.4,GB/T 2358-1994标准[9]建议取rp=0.44, JB/T 4291-1999 标准[10]建议取rp=0.45,我国标准最近修正为rp=0.4[11],同国际标准及英国系列标准一致。由几何上的相似可以得出
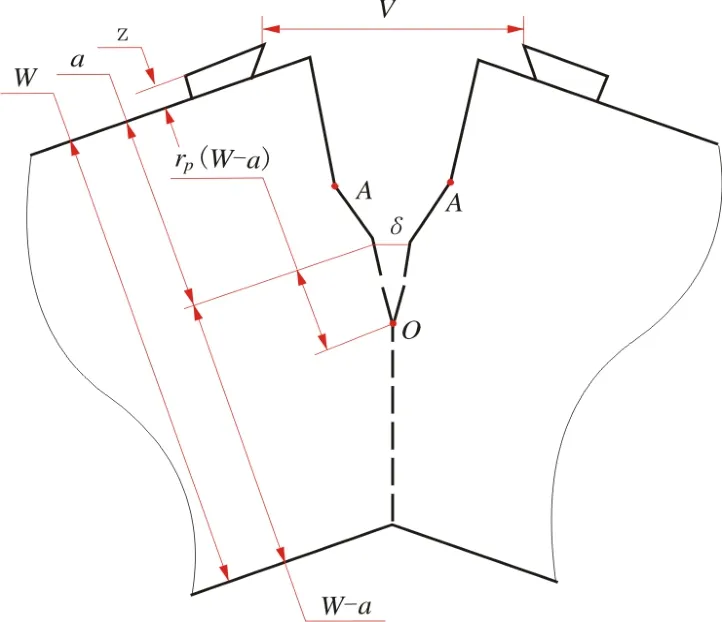
图5 CTOD试验原理示意图
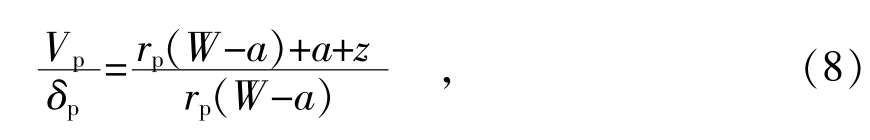
经变换得到

δ为原始裂纹张开的总位移,它包括塑性部分δp和弹性部分δe

则原始裂纹张开总位移为
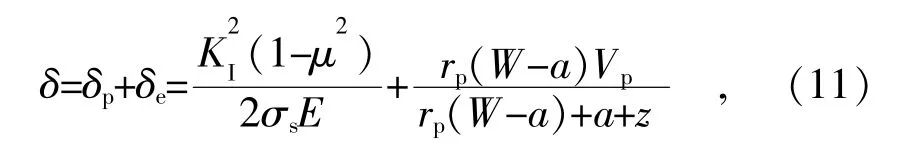
式(10)中:E-材料的弹性模量;
σs-材料的屈服强度;
-材料的泊松比;
KI-材料的应力强度因子。
材料的应力强度因子计算公式为
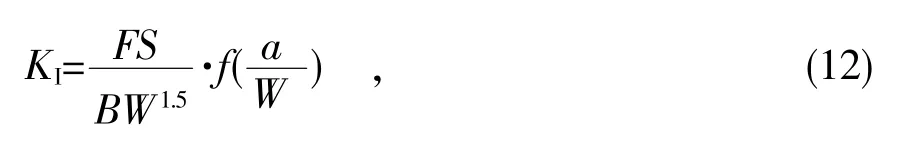
式中:F-三点弯曲试验荷载;
S-三点弯曲试样的总跨距;
B-三点弯曲试样的厚度。
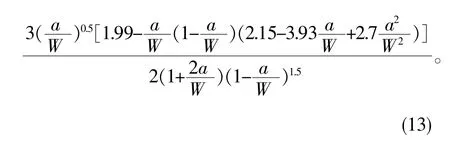
2.2 CTOD 试验部分(测 δc)
2.2.1 材料力学性能
试验用X80钢的力学性能见表2。

表2 X80钢力学性能
2.2.2 X80 钢 CTOD(δc值)测试
试验参照英国标准BS 7448:Part 1《断裂力学韧性试验:金属材料KIC、临界CTOD值和临界J积分值的确定方法》[8]进行。CTOD试验的环境温度为-20℃±2℃。试验采用单试样方法,在MTS-810C电液伺服材料试验机上进行。试验采用带单边预制疲劳裂纹的标准三点弯曲试样,试样截面采用2B×B形。切口取向为NP方向,其中N为垂直于焊缝方向,P为平行于焊缝方向。按照规范BS 7448对10 mm厚X80钢进行了-20℃的CTOD低温韧度试验。本试验试样编号分别为BH1,BH2和BH3。厚度B=10 mm,跨度S=80 mm。
试验测得X80试样断裂韧度δc见表3,从表3可以看出,10 mm厚X80钢在低温-20℃时断裂韧度δc最小值为0.074 mm。
三点弯曲试样压断的断口如图6所示。
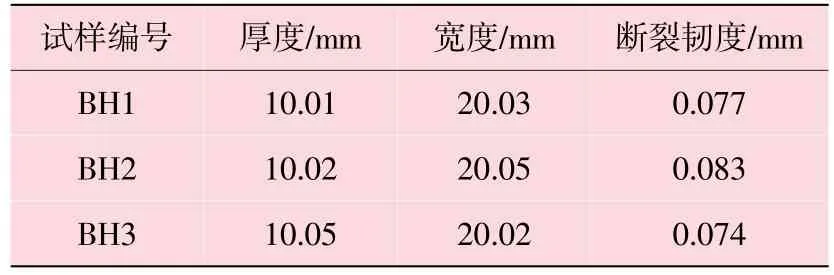
表3 X80试样主要参数及断裂韧度值

图6 试样断口形貌
3 断裂韧度评估
Wells首先提出弹塑性条件下的CTOD断裂判据,δ≤δc。式中δ指裂纹体受载后,在原裂纹尖端垂直于裂纹方向的裂纹尖端张开位移δ,断裂韧度评估结果见表4。
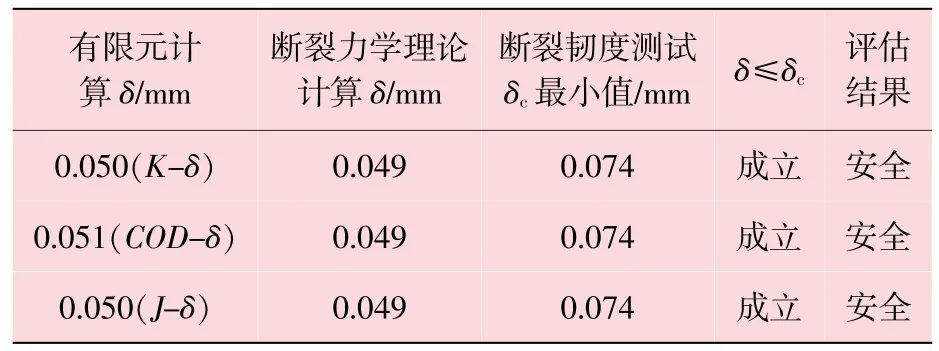
表4 断裂韧度评估结果
4 结 论
(1)采用KSCON命令构造裂纹尖端奇异单元计算的二维弹性阶段的应力强度因子KI精确性很高,与断裂力学理论结果误差很小。
(2)按照本文X80钢板受力模型,采用K-δ方法,COD-δ方法和J-δ方法计算的δ分别为0.050 mm,0.051 mm和0.050 mm。
(3) 采用 K-δ方法、 COD-δ方法和 J-δ方法计算的δ值和按断裂力学理论计算的δ值误差在允许范围内。
(4)10 mm厚X80钢在低温-20℃时断裂韧度δc最小值为0.074 mm。
(5)采用CINT命令计算J积分与断裂力学理论计算误差在允许范围内,采用CINT命令计算J积分有效。
(6)按照CTOD断裂判据成立,因此X80钢薄板存在含中心I型穿透性裂纹,裂纹长4 mm,板宽80 mm,板长100 mm,厚度10 mm在 “无限远”处有双向均匀拉应力10 MPa,经过断裂韧度评估结果为安全。
[1]武战学.X80钢管焊接接头断裂韧性试验分析[J].焊管,2011,34(03):29-32
[2]曾攀.基于ANSYS平台有限元分析手册结构的建模与分析[M].北京:机械工业出版社,2012:300.
[3]GUBELJAK N,SEMENSKI D,DRVAR N,et al.Object Grating Method Application in Strain Determination on CTOD Tests[J].Strain,2006(42):81-87.
[4]苗张木.厚钢板焊接接头韧度CTOD评定研究[D].武汉:武汉理工大学,2005:22.
[5]薛河.基于CTOD方法的焊接结构缺陷工程评估方法的研究[D].西安:西安交通大学,1998:31.
[6]李庆芬.断裂力学及其工程应用[M].哈尔滨:哈尔滨工程大学出版社,1998:82.
[7]陈靳,赵树山.断裂力学[M].北京:科学出版社,2006:133.
[8]BS 7448:Part l,Method for Determination of KIC、Critical CTOD and Critical J Values of Metallic Materials[S].
[9]GB/T 2358-1994,金属材料裂纹尖端张开位移实验方法[S].
[10]JB/T 4291-1999,焊接接头裂纹张开位移(COD)实验方法[S].
[11]GB/T 7732-2008,金属材料表面裂纹拉伸试样断裂韧度试验方法[S].
