基于模糊PID的Smith预估碱液温控系统

邢健峰，纪志成

（江南大学 电气自动化研究所，无锡 214122）

工业控制过程中时间滞后是一个普遍存在的现象，对于时滞时间较小的控制系统，可以通过常规的PID控制器进行控制，但对于时间滞后较大的控制系统，常规的控制方法常无法满足工业上的控制要求。对于一些大时滞的系统来说，现阶段存在多种解决办法，如预测时滞PI控制网络[1]，基于Smith预估器的PID控制系统[2]，具有内膜结构的PI/PID控制系统[3]，这些控制系统都取得较好的控制效果，但是，它们都缺乏一定的自适应机制。在工业控制系统中，工况的不同会伴随着多种过程量的变化，需要控制系统根据不同工况进行自适应的变化。

温度控制具有滞后性，使得被控量不能及时反映控制器的动作，控制信号要延迟一段时间才能反映到被控量上，同时当系统中存在扰动时，控制器无法及时对干扰信号产生抑制作用[4-6]，若采用传统的PID控制器对被控量进行控制，在滞后时间较长的情况下，控制系统无法达到控制要求。采用Smith预测器控制可以有效的减少因为时滞而对系统产生的影响，但是，Smith预测控制要求系统具有一个精确的数学模型，而对这样一个工业控制系统而言，常常无法测量这样一个精确的过程模型，而模糊控制是基于模糊原则，不需要精确的控制模型，对这样的控制系统而言更加适合[7-9]，模糊PID控制对变化的系统模型具有更好的控制效果。所以，采用基于Smith预测的模糊PID控制器对温度进行控制。

1 脱盐水系统中的碱液加热系统

在脱盐水控制系统中再生区部分，为了使碱液在温度较低的环境下保持要求的流速，在其出口处加入了温度换热装置，使用温度较高的蒸汽对其进行加热处理，为了更好的控制加热温度，一般会在蒸汽出口处安装蒸汽调节阀，控制蒸汽的大小。

这一系统对于碱液流速的控制非常重要，在脱盐水工业过程中，再生时往往希望酸液与碱液流速基本相同，但在温度较低的情况下，碱液流速相对较慢，若不进行较好的温度加热，会使碱液流速不确定，无法进行相应工艺参数的设置，同时，由于碱液的温度高低变化，可能造成再生不彻底等后果，影响整套脱盐水系统的产水质量，对于脱盐水系统来说，控制碱液温度换热器的温度至关重要。

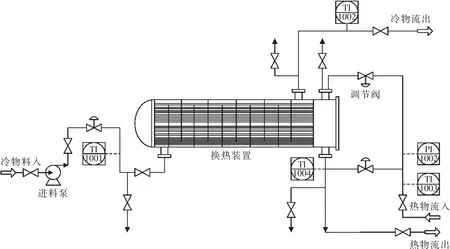
图1 换热器工作流程Fig.1 Heat exchanger working process

碱液换热的工作流程如图1所示。对于这样的温度控制系统，因为其具有大时滞的特点，采用常规的PID控制往往无法满足控制要求。故本系统采用了Smith Fuzzy-PID控制策略。

2 控制器设计

2.1 控制结构原理

本控制系统的结构如图2所示。

图2 系统结构图Fig.2 System Structure

图中设输入为 R（s），输出为 Y（s），PID 控制器的传递函数为Gc（s），Smith预估器的传递函数为Gm（s）（1--θmse ），系统过程传递函数 G0（s）e-θs。其中 θm是控制对象纯滞后时间的估计值，θ是系统纯滞后时间。根据如图所示的控制系统模型所计算的传递函数为

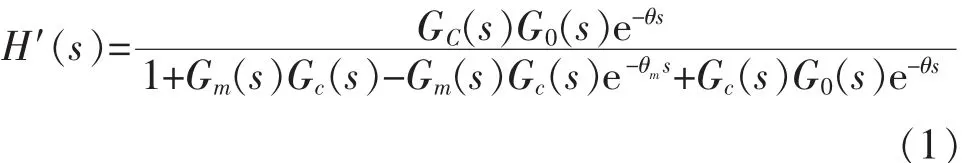
在控制系统完全补偿的情况下，得到Gm=G0，θm=θ，故式（1）可以简化为

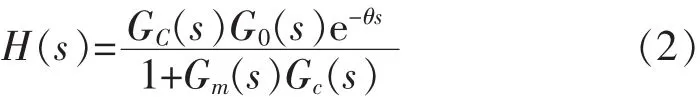
由式（2）可以看到，系统延时e-θs是在整个系统外，对系统的稳定性不再造成影响。因此Smith预测器成功去除了有时存在时滞而对系统稳定性造成的影响。

系统中将Smith预测器与模糊PID控制器结合，避免了Smith对参数过于敏感的问题，通过模糊控制器对PID的3个参数进行自整定调节，使控制器性能进一步提高[10-11]。

2.2 模糊控制器设计

自整定PID控制器中模糊推理的输入为偏差e和偏差变化率ec，输出 为 PID 参 数 的 修 正 量 （ΔKP，ΔKI，ΔKD）。 将输入 e，ec 与输出 ΔkP，ΔkI，ΔkD转化到模糊论域，分别记为E，EC，UP，UI，UD。 取模糊论域为［-3，3］，并分为七档：负大，负中，负小，零，正小，正中，正大，简记为 NB，NM，NS，ZO，PS，PM，PB。脱盐水系统中，应保持碱液温度在（40±9）℃，取温度偏差 e为（-9，9），偏差变化率 ec 为（-3，3），故可计算出量化因子Ke=0.33，Kec=1。系统中模糊控制的隶属函数取高斯型，解模糊方法取加权平均法。图3为其隶属函数曲线。

图3 隶属函数曲线Fig.3 Membership function

常规PID控制器中3个参数的作用不同，其中比例系数KP使控制系统具有快速的响应速度，积分系数KI主要改善系统的静态特性，提高静态精度，微分系数KD可以控制系统的震荡，减少超调，改善控制系统的动态特性。根据P、I、D 3个参数的作用和模糊控制器的输入E，EC的不同，将模糊控制器的模糊规则总结如下[12-14]：

当系统偏差|e|较大时，为了使系统具有较快的响应速度，应取比例系数KP较大，为了避免积分饱和，应取积分系数KI较小，同时为了使系统不出现较大的超调，应取微分系数KD为零。

当系统偏差与变化率的乘积为负时，即e×ec＜0时，说明系统偏差具有减小的趋势，如果偏差|e|较大，可取中等的KP，较小的KI和中等的KD，以提高系统动态与稳态特性，如果偏差|e|较小，应增大KP和KI，保证系统具有良好的稳态特性，同时为了使系统具有较好的抗干扰性和减少在稳定值点的震荡，应取适量的KD。

当系统偏差与变化率的乘积为正时，即e×ec＞0时，说明系统偏差具有增大的趋势，如果|e|和|ec|具有中等大小时，应取较小的KP，和适中大小的KI和KD，使系统具有良好的跟随特性和较小的超调，如果|e|较大，为保证系统的响应速度，可取中等大小的KP，较小的KI和中等大小的KD，如果|e|较小，可取中等的 KP，较大的KI和较小的KD，保证系统的稳定性。

根据上述原则，可将其转化成模糊控制语句，如：

If E=NB AND EC=NB then KP=PB，KI=ZO，KD=PS

总结出模糊控制规则表如表1所示。

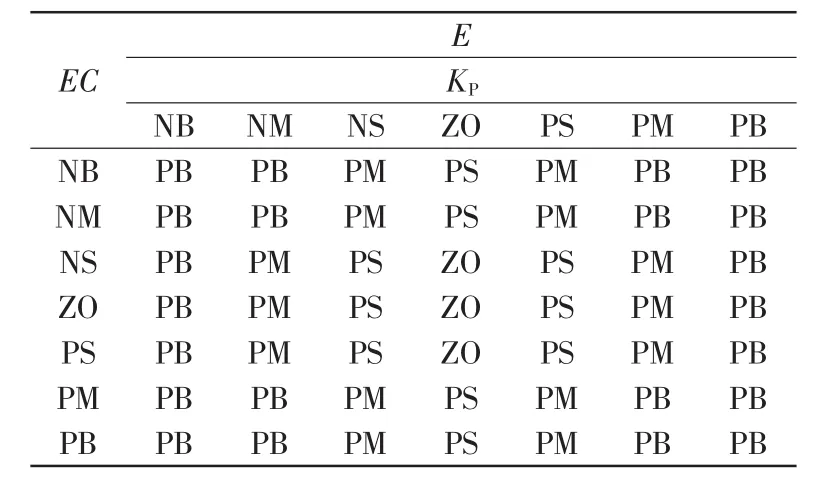
表1 KP参数的模糊规则表Tab.1 Fuzzy rules of Kp

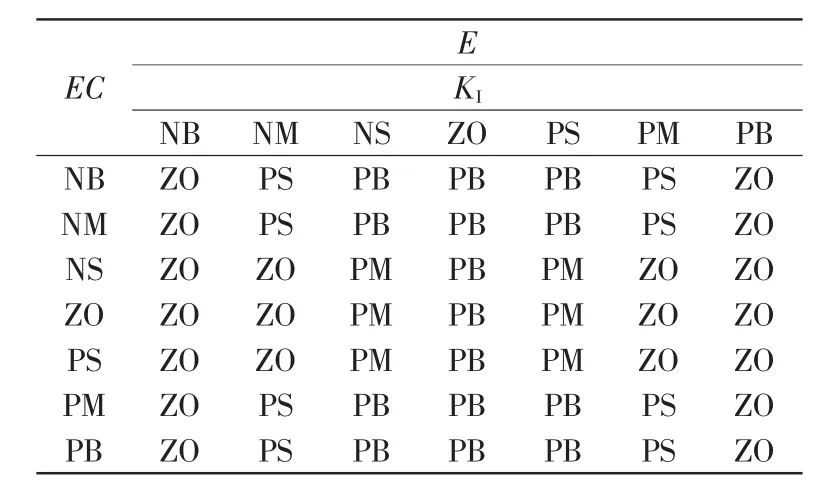
表2 KI参数的模糊规则表Tab.2 Fuzzy rules of KI

表3 KD参数的模糊规则表Tab.3 Fuzzy rules of KD

3 仿真分析

依据以上所述，在Simulink中对控制系统进行搭建，将温度换热过程抽象成一阶惯性环节：

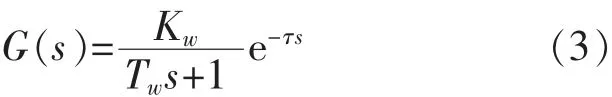
式中：Kw为系统放大倍数；Tw为供水系统惯性时间常数；τ为系统纯滞后时间。

设Kw=1，Tw=500，对基于Smith预测器的模糊PID控制器进行仿真，同时，仿真模型搭建一条常规PID控制回路对其进行对比。系统仿真Simulink模块如图4所示。

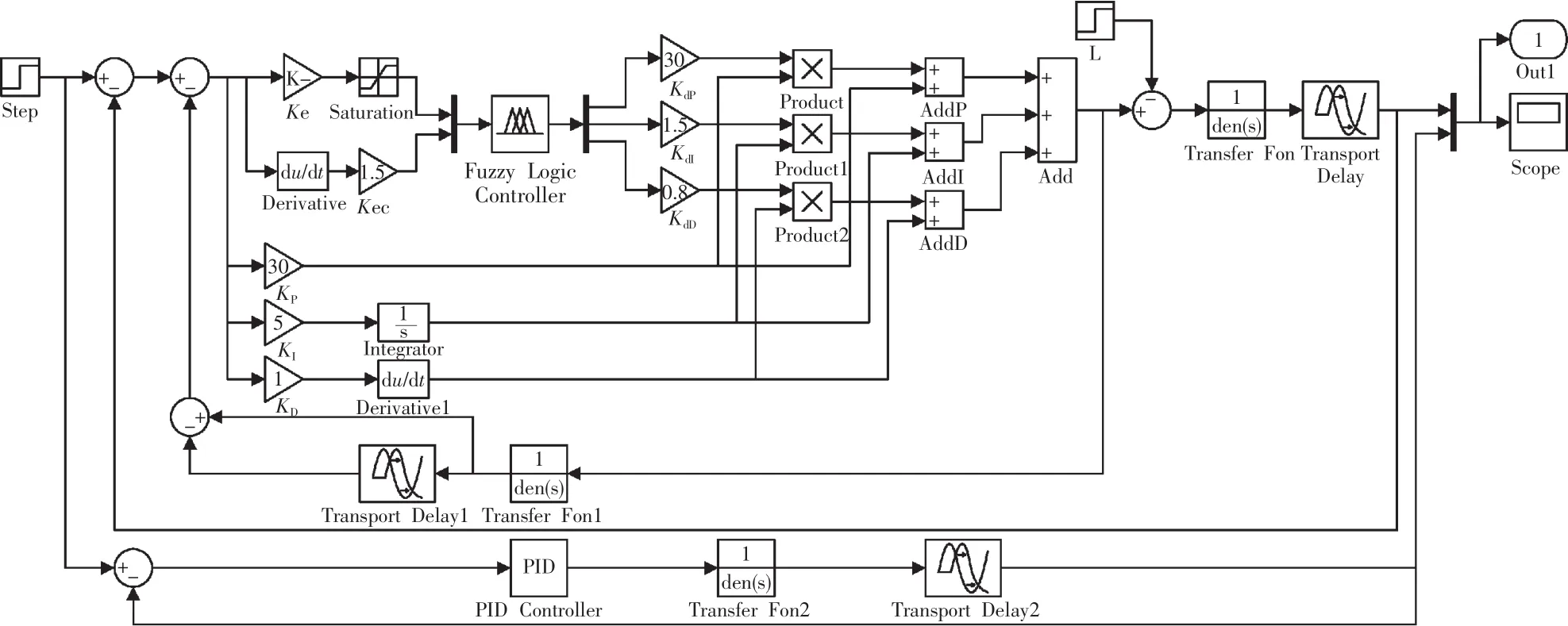
图4 SIMULINK模块Fig.4 SIMULINK module

依据现场实际经验，PID 3个参数在KP＝30，KI=5，KD=1时控制效果最好，在回路中不加入时滞时的仿真波形如图5（a）所示，在加入一定时滞后，PID控制器已经无法对回路进行控制，仿真结果如图 5（b）所示。

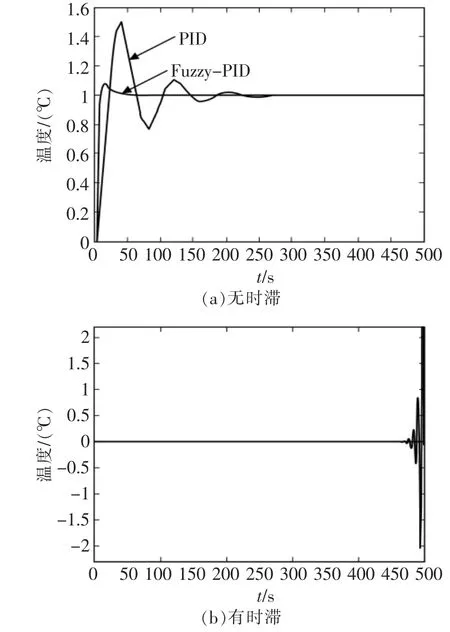
图5 仿真曲线Fig.5 Simulation curve

将Smith预测器加入至PID控制回路中，对回路中延时进行补偿，设定延时时间30 s，再次对系统进行仿真，其仿真曲线如图6（a）所示。设定Tw=800，延时时间60 s，再次对系统进行仿真，仿真结果如图6（b）所示。

图6 仿真曲线Fig.6 Simulation curve

从仿真结果上看，在控制系统中加入Smith预测器很好地克服了时滞对系统带来的影响，使系统中的时滞转化为时间延时，克服了传统PID控制无法进行大时滞系统的控制，在控制器中加入了模糊控制器，对PID参数进行在线整定，提高了控制器的性能，从结果上看，模糊PID与传统PID控制器相比，在响应速度、超调量、稳态精度上有很大的提升。

4 Smith预估器在PLC中的实现

现阶段，大多数工业控制系统中的主控制器都是采用PLC进行实现的，在PLC中实现基于Smith预测器模糊PID控制方法如下，Smith预估器的数学模型为 Gm（s）（1-e-θm），将其分解成两部分，一部分为 Gm（s），另一部分为-Gm（s） e-θm。其中在完全补偿的情况下，Gm（s）应于系统模型相同，即 Gm（s）形式为一阶惯性系统G（s）=。在 PLC 中实现传递函数需要调用S7 PLC中的PROC_C模块，这个模块模拟了一个三阶传递函数，其形式为

其中：GAIN为系统增益；TM_LAG1为时间延迟1，单位：s；TM_LAG2 为时间延迟 2，单位：s；TM_LAG3为时间延迟3，单位：s。将其中TM_LAG1与TM_LAG2设定为0，即可以实现对一阶惯性系统的模拟。

纯滞后e-θs环节需要调用PLC中FB22，其中定义有一个队列，按照先进先出的原则，程序每循环一次队列向前移动一格，经过n格后，时滞时间τ为n倍的采样时间，利用间接寻址实现系统延时。其主要程序如下：

back：T#temp2

L#templ

L 2#1000

*I

L 80

+I

LARl

L DID[ARl，P#4.0]

T DID[ARl，P#0.0]

L#templ

L 4

+I

T#templ

L#temp2

L00P back

通过PROC_C与FB22的调用与赋值可以很好的实现Smith预测器。

5 结语

综上所述，针对脱盐水中碱液温度换热系统的实际情况，采用这种自整定PID的Smith预估器控制方案克服了其大时滞、时变性、工况复杂等特点，从而保证了该轮胎生产企业的脱盐水系统出水水质稳定，节约水资源，减少污水排放，提高了生产效率。这种控制系统在控制器性能上与传统的控制方法相比具有很大的提高，并且实现方法较为容易，控制效率较高，比较实用于工业控制系统，在生产实际中有着很高的推广价值。

[1] 任正云，韩佰恒，王小飞，等.预测PI和准预测PI控制算法在片烟复烤机上的应用[J].烟草科技，2009（11）：21-25.

[2] 罗海波.PID控制器设计与仿真研究[J].计算机仿真，2012，39（2）：345-348.

[3] 陆平，赵捷，郭鹏.模糊内模PID控制及应用[J].自动化仪表，2012，33（3）：50-52.

[4] 刘川来，杨朋飞，宁通.纯滞后串级控制系统的新型控制算法[J].信息与控制，2009，38（2）：245-248.

[5] 李丽娜，柳洪义，罗忠，等.模糊PID复合控制算法改进及应用[J].东北大学学报：自然科学版，2009，30（2）：274-277.

[6] 诸静.模糊控制原理与应用[M].北京：机械工业出版社，2005.

[7] Lai Chien-Liang，Hsu Pau-Lo.Design the remote control system with the time-delay estimator and the adaptive smith predictor[J].IEEE Transactions on Industrial Informatics，2010（1）：73-80.

[8] 张海涛，李珍.基于Smith预估补偿的网络控制系统仿真研究[J].计算机工程与应用，2012，48（8）：243-245.

[9] 李涛，蒲鸿春，冯宇，等.Fuzzy-Smith控制器在pH值控制中的应用[J].仪器仪表与分析监测，2009（2）：10-11.

[10]文定都，何玲.基于Smith模糊PID控制算法的炉温控制系统[J].仪表技术与传感器，2009（4）：107-108，117.

[11]姜文佳，姜永健，姜广田，等.模糊-PID控制算法改进及在温控系统中的应用[J].控制工程，2006，13（4）：338-340.

[12]路昀菲，孟彦京，金岩.基于自适应模糊PID的真空玻璃传热系数测量仪[J].化工自动化及仪表，2012，39（5）：598-600.

[13]刘向东.模糊PID在湿法脱硫pH控制中的应用[J].电力环境保护，2009，25（3）：15-18.

[14]王春艳.基于Smith预估模糊PID控制的加热器温控系统[J].自动化与仪表，2012，27（6）：49-52.