细菌群体趋药性算法在多元非线性回归分析中的应用

王雪红 刘晓青

（河海大学水利水电工程学院，南京 210098）

在实际生产、生活以及科学研究中为了及时、准确、全面、系统地掌握事物的性态及发展趋势，需要对观测得到的数据按照科学的理论和方法进行分析统计、回归预测等.

随着科技水平的提高，根据实测数据进行分析的理论、方法得到了较大的发展并已应用于工程实际中.最小二乘法容易通过计算机的简单程序实现，程序已经模块化，用户使用起来比较方便，对工程观测资料的分析多采用最小二乘法.但由于最小二乘法在求解时需要对估计目标函数求导，过程比较繁琐，还要求优化模型具有连续、可导的性能，因而对于非线性问题，可能遇到函数不可导的情况而难以找到全局最优解.近年来，BP人工神经网络（BP－ANNs）［7］、遗传算法（GA）［10］、群体智能算法如：蚁群算法（ACO）［8］、粒子群算法（PSO）［9］、人工鱼群算法（AFSA）［11］、人工蜂群算法（ABC）［3］等一些新兴的智能算法在求解多元回归问题中得到越来越普遍的应用，但是这些智能算法在应用中会出现易陷入局部最优、早熟、收敛速度慢、稳定性差等问题，不少学者试图通过算法的混合来提高计算性能并取得了一定的效果.

细菌群体趋药性算法是一种考虑单个细菌活动和细菌之间关系的混合算法，其优化速度和精度超过了其他一些常见的群体优化算法［1］.细菌群体趋药性算法源于细菌趋药性算法，早期细菌趋药性算法的研究是基于Berg、Brown和Dahlquist提出的细菌趋药性微观模型，Sibvue D.Muller及其同事们在此基础上进一步综合，并且结合最新的生物学研究成果提出了细菌趋药性算法（Bacterial Chemotaxis，BC）［6］；国内最先研究该算法的浙江大学李威武等［1］通过研究模拟细菌个体间的信息传递与共享机制，在基本BC算法的基础上引入了群体交互概念，从而提出了细菌群体趋药性算法，它极大地提高了细菌趋药性算法的优化能力，且优化速度和精度较好.本文利用细菌趋药性算法进行多元非线性回归分析并将其应用到混凝土重力坝位移的监测中，为解决混凝土坝监测中的回归问题提供了一种新方法.

1 多元回归数学模型

1.1 多元线性回归的数学模型

假如变量y与另外p个变量x1，x2，…，xp的内在联系是线性的，它的第k试验数据是（xk1，xk2，…，xkm，yk），k＝1，2，…，N，则数据有如下的结构形式：

式中，β0，β1，…，βm是m＋1个待估计参数；x1，x2，…，xm是m个观测或可以确定的一般变量；ε1，ε2，…，εn是n个相对独立且服从同一正态分布N（0，σ2）的随机变量.

若令

则数学模型可以写成：

其中，ε是n维随机变量，它的分量是相互独立的.

1.2 多元非线性回归的数学模型

非线性回归模型的一般形式为

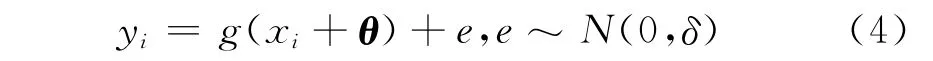
式中，xi为系统输入量，yi为系统输出变量，θ＝［θ1，θ2，…，θk］T为待定参数向量，e为服从正态分布的随机变量，（xi，yi）是已知数据对，i＝1，…，n.该非线性回归数学模型的求解就是根据已知数据对求解向量θ，求解偏差平方和使

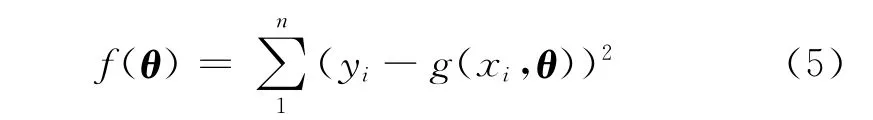
最小，非线性回归模型参数优化问题实质就是非线性函数优化问题［2］.

2 细菌群体趋药性算法（BCC）

2.1 算法的基本原理

BC算法是从生物行为中获取灵感的方法，很多学者对生物体对自身环境的反应进行了研究［3－4］.假定细菌的轨迹是由一系列直线组成的，细菌运动速度一样；细菌改变运动方向时，向左或向右的概率相同；细菌在各段轨迹上移动时间和各段轨迹间的夹角都由概率分布决定；夹角和时间的概率分布和先前轨迹的参数无关.BCC是在BC的基础上提出来的，假定细菌在引诱剂环境中通过一些简单的假设方式进行通信.细菌不仅使用自己的运动位置信息也利用其他细菌的位置信息进行函数优化［1］.

2.2 算法的计算步骤

BCC算法应用于多维函数优化的步骤：

T0为最小平均移动时间、tc为相关时间、b为与维数无关的参数［6］.

1）计算细菌的移动速度v.通常假定其为常数1；

2）计算细菌在新方向上的移动时间t.其数值由概率分布决定：

式中，T0为最小平均移动时间，fpr为当前点和上一个点的函数值的差，1pr为变量空间中连接当前点和上一个点的向量的模.

3）计算新的运动方向.新方向通过在平面（xi，xi＋1）上的φi使用高斯概率密度分布来计算，其中φi从坐标轴xi测量，用来判断向左或向右转，分别为

其中，φi∈［0°，180°］

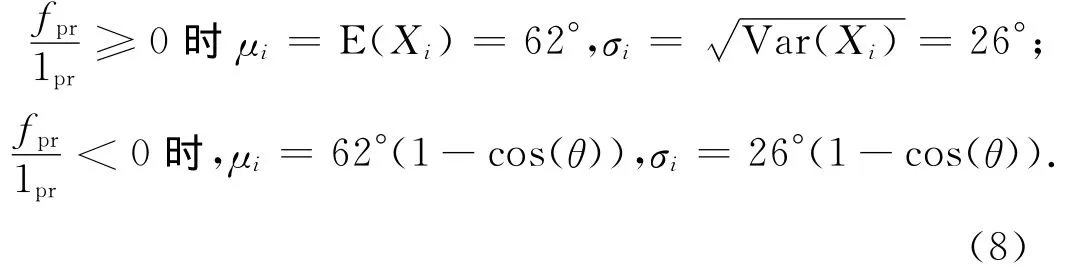
向左或向右采用同样的概率密度分布，因而φi的概率密度分布为

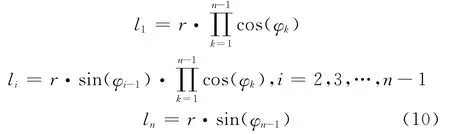
细菌在每次移动到新位置之前，要感知它周围的环境，试探旁边是否有其他位置更好的细菌.如果有，那么它有可能趋向移动到这些拥有较好位置细菌的中心点.在移动步数为k时细菌i附近有更好位置的同伴的中心点由下式决定：

rand（0，2）指（0，2）之间的随机数.

3 细菌群体趋药性算法在回归分析中的实现

为了验证细菌趋药性算法在回归分析中应用的可行性，以混凝土重力坝位移模型为研究对象，取溢流坝段坝顶某部位测点2010年1月10日～2012年8月5日（每天观测一次）顺河向位移、水位、温度、时间数据各142个.由于篇幅有限各数据不一一列出，仅给出某测点顺河向位移及上游库水位随时间变化过程线，如图1所示.

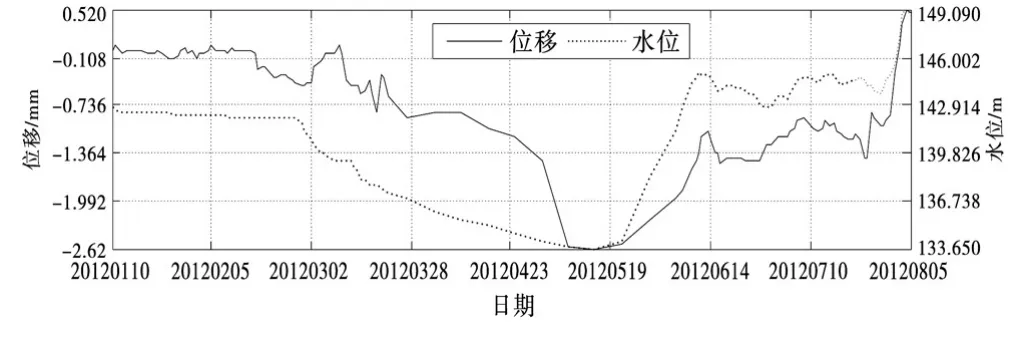
图1 某测点顺河向位移及上游库水位随时间变化过程线

回归的实质就是使ffitness＝∑（δ－＾δ）2趋近于0，其中δ为实测值；＾δ为预报值.

做回归分析之前根据3σ原则提出数据中的奇异点，首先将多项式＾δ中的每一项中的已知值计算出来，转化为线性模型的形式，使用matlab中的lsqcurvefit进行多元非线性回归分析；然后，采用BCC算法优化该回归分析问题中的未知参数及∑（δ－＾δ）2，选取最大迭代步数500、细菌个数50，各参数的初始取值范围参考利用最小二乘法得到的参数取值区间，所得结果见表1.最小二乘法和BCC算法所得到的复相关系数都比较大，可用于短期内位移的预报分析.

表1 回归模型参数及复相关系数表

由表1可以看出，利用BCC算法所得参数与最小二乘法所得参数基本一致，说明该算法在优化多元函数回归参数问题中是可行的、有效的，参数值也较稳定.另外，最小二乘法和BCC算法得到的∑（δ－＾δ）2分别为6.514 1、6.246 7，即BCC算法得到的∑（δ－＾δ）2较小.使用Matlab2012a进行运算，最小二乘法的系统响应时间为6.482 8s，BCC算法的系统响应时间为5.064 7s，在相同样本数条件下，基于BCC算法回归分析的系统响应时间小于基于最小二乘算法回归分析系统响应时间.

4 结 论

细菌群体趋药性算法采用了细菌群体交互模式，各细菌的移动步长按照概率分布随机取值，具有突破局部最值限制的寻优机制，因而大大提高了细菌的全局寻优性能且具有很好的收敛速度和计算精度，具有极大的研究发展潜力.

本文利用细菌群体趋药性算法进行回归分析，虽然模型采用参数个数、数据较多，且各组数据具有一定的随机性，但也取得了相对满意的结果且比最小二乘法计算得到的观测值和预报值之间的误差平方和∑（δ－＾δ）2小，且基于BCC算法回归分析的系统响应时间小于基于最小二乘算法回归分析系统响应时间.说明了BCC算法应用于回归模型参数估计是可行的，效果也较传统的最小二乘法好，从而为回归分析提供了一种新思路.另外，对细菌群体趋药性算法采取一定的改进策略来提高寻优速率，可使其更好地应用于生产生活中.

［1］ 李威武，王 慧，邹志君，等.基于细菌群体趋药性的函数优化方法［J］.电路与系统学报，2005，10（1）：58－63.

［2］ 陆克中，方康年.PSO算法在非线性回归模型参数估计中的应用［J］.计算机技术与发展，2008，18（12）：134－136.

［3］ 张姣玲.人工蜂群算法在多元线性回归中的应用［J］.广东技术师范学院学报：自然科学，2011（3）：31－33.

［4］ Dorigo Marco，Maniezzo Vittorio，Colorni Alberto.Ant System：Optimization by a Colony of Cooperating A－gents［J］.IEEE Transaction on SMC，Part B，1996，26（1）：29－41.

［5］ 吴中如.水工建筑物安全监控理论及其应用［M］.北京：高等教育出版社，2003.

［6］ Muller S D，J.Airaghi Marchetto S，Koumoutsakos P.Optimization Based on Bacterial Chemotaxis［J］.IEEE Transaction of Evolutionary Computation，2002，6（1）：16－29.

［7］ 辛大欣，王长元，肖 峰.BP神经网络在回归分析中的应用研究［J］.西安工业学院学报，2002，22（2）：129－35.

［8］ 吴新杰，陶崇娥，李 媛.混沌蚁群算法在回归分析中的应用［J］.辽宁大学学报：自然科学版，2007，34（2）：101－103.

［9］ 刘锦萍，郁金祥.基于改进的粒子群算法的多元线性回归模型参数估计［J］.计算机工程与科学，2010，32（4）：104－105.

［10］郭朝有，贺 国，陈国钧.遗传算法在非线性回归模型辨识中的应用［J］.海军工程大学学报，2003，15（2）：70－73.

［11］李 媛.基于人工鱼群算法的多元线性回归分析问题处理［J］.渤海大学学报：自然科学版，2011，32（2）：168－171.