Risk Theta*:一种基于地形危险度的任意航向路径规划算法

王琼,于登云,贾阳

(1.探月与航天工程中心,北京100037;2.北京空间飞行器总体设计部,北京100094; 3.中国航天科技集团公司,北京100048)

Risk Theta*:一种基于地形危险度的任意航向路径规划算法

王琼1,2,于登云3,贾阳2

(1.探月与航天工程中心,北京100037;2.北京空间飞行器总体设计部,北京100094; 3.中国航天科技集团公司,北京100048)

提出了一种基于地形危险度的任意航向路径规划算法——Risk Theta*。首先以星球表面地形特征统计分析为基础提出了地形危险度指标,并建立地形危险度地图。在此基础上应用Basic Theta*搜索,以危险度最低为方向搜索最优路径。仿真实验证明,该算法能够在栅格地图上找到比A*和Basic Theta*算法危险度低得多、长度相当的任意航向路径,既显著提高了巡视器的安全性,又满足了星球巡视探测对任意航向行驶的迫切需求,因此具有较强的实用性。

Theta*;地形危险度;路径规划;任意航向;启发式搜索

0 引 言

星球巡视器的全局路径规划是指在已知的星球表面非结构化复杂环境中,寻找一条从起始点到目标点的最优或近似最优的无碰路径,以实现巡视器的安全移动。全局路径规划算法大多采用基于几何模型搜索的思路,首先构建巡视器环境空间的几何模型,在此基础上采用某种图搜索算法,得到最优路径。几何模型构建主要有路径图法和单元分解法两类,其中路径图法和精确单元分解法的最大缺点是图的构建过程比较复杂,建模成本较高;而栅格法是一种近似单元分解法,十分便于创建、存储和使用,如数字高程图(DEM)就是一种广泛应用的栅格地图。图搜索算法包括宽度优先、深度优先、迭代加深、Dijkstra、A*等各种算法,其中以A*算法为代表的启发式算法具有搜索效率高、容易实现、算法完备等优点。因此,基于栅格地图的启发式算法得到了广泛的研究和应用。

但是,A*算法在栅格地图中的搜索方向和路径方向受到相邻8个栅格的限制,无法得到最优路径。而规划出任意航向的最短路径恰恰是星球巡视探测、野外车辆导航、计算机游戏等领域的迫切要求。为了解决这一问题,在A*算法基础上,研究人员提出了一些改进算法。

A*with post-smoothing paths算法[1]对A*算法结果进行后处理,得到更平滑路径,但是不能保证找到最短路径。Field D*算法[2]采用线性插值,使得路径点不局限于栅格中心或四角,消除了相邻栅格之间的离散状态转移所带来的路径不平滑问题,但是路径中经常存在不必要的转向。Block A*算法[3]分块预存事先计算好的块内各边界点之间距离,并按块进行操作和搜索,能够得到任意方向的路径,这种以空间换时间的策略极大地提高了计算速度,但是按块拼接的路径往往也不是最短路径。A Nash等人结合A*算法和可视图法的优点,提出了Basic Theta*和Angle-Propagation Theta*(统称为Theta*)算法[4],通过引入父节点和后继节点间的可视性检查来寻找捷径,可以找到任意方向的路径,并且在计算效率和最优性方面都有很好的表现。

本文在地形特征统计分析基础上,设计了地形危险度指标,提出了一种以危险度最低为优化方向的Theta*改进算法——Risk Theta*。

1 Basic Theta*算法

Basic Theta*算法与A*算法的主要差别在于扩展节点时的程序。Basic Theta*在A*的基础上,将当前节点s的相邻节点s′与s的父节点sparent做一次可视性检查,若可视,则比较从sparent直接到s′和从sparent经s到s′这两条路径的代价,选择代价更小的路径。

A*和Basic Theta*扩展节点程序分别见算法1和算法2。其中,OPEN为一个用于存放当前待扩展节点的列表,CLOSED为一个用于存放已经访问过节点的列表,LineOfSight(s,s′)表示判断s与s′是否可视,Insert(·)和Remove(·)分别表示从列表中插入节点和移出节点。

但是,Basic Theta*算法仅仅将栅格简单区分为可通行和障碍,并且只在可通行栅格中搜索最优路径。但实际上在星球表面复杂地形环境中,即便是可通行栅格也存在着地形高低起伏带来的行驶危险度差异,这是不可忽视的。若长期在这些高危险度栅格上行驶,会导致巡视器磨损加重,甚至陷入困境。因此,在星球表面巡视探测任务中,基于二值障碍判断的Theta*算法的路径解安全性较差,应用效果不佳。

算法1 A*算法

算法2 Basic Theta*算法

2 Risk Theta*算法

众所周知,人类在陌生野外环境中进行探险时的本能反应是保持高度警惕,实时评估自身所处危险程度,及时应对各种威胁。类比人类的这种行为决策方式,由于任务机会极其难得、造价昂贵等原因,巡视器在星球表面非结构化未知环境中进行探测时也应遵循安全至上的法则,其次才考虑追求更短的距离和更高的效率。基于这一思路,本文提出地形危险度指标,来刻画巡视器行驶在某一地形上所面临的危险程度,作为Theta*搜索的优化方向。

2.1 地形特征分析

在定义地形危险度指标之前,先进行地形分析,首要工作是提取坡面地形因子。地形因子包括微观和宏观两大类,前者反映了微观地表单元的形态、起伏或扭曲特征,后者反映了地貌的宏观形态特征[5]。考虑到与巡视器姿态稳定性、越障能力等的相关性,本文选取了坡度这个微观因子和地形粗糙度、地形起伏度两个宏观因子进行计算。

提取地形因子通常需要开辟一个有固定分析半径的分析窗口(可称为地块),并且在窗口内进行统计计算。按照巡视器车体尺寸划分地块,可以在计算量和精度之间达到较好的平衡。

1)坡度

坡度表示月表面在某一点的倾斜程度,在数值上等于过该点的月表微分单元的法矢量ni,j与坐标系z轴单位矢量z的夹角,即

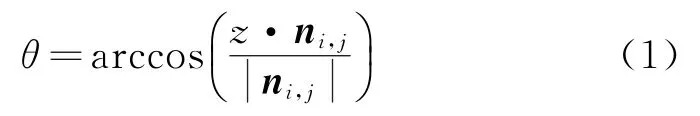
假设该月表微分单元的拟合平面方程为z= Ax+By+C,则平面法矢量为ni,j={A,B,-1},z轴单位矢量为z={0,0,1},故有

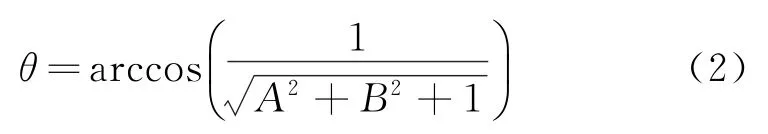
其取值范围为0°～90°。

2)地形粗糙度

地形粗糙度是反映地形的起伏变化和侵蚀程度的指标,一般定义为地表单元的曲面面积S曲面与其在水平面上的投影面积S水平之比,即

地形粗糙度可以通过拟合残差来计算,即地块内所有点与拟合平面高程偏差的平方和

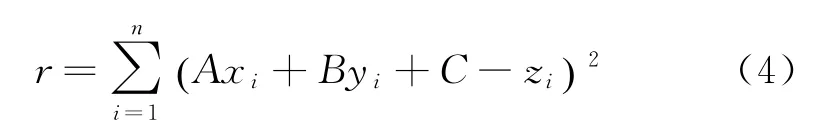
式中:n为地块内的栅格数。

3)地形起伏度

通常地形起伏度定义为地块内最大高程与最小高程之差,但这样的定义难以区分是斜坡还是障碍造成的地形起伏。为了刻画障碍的影响,本文将地形起伏度定义为地块内每两个相邻栅格的高程差的最大值。

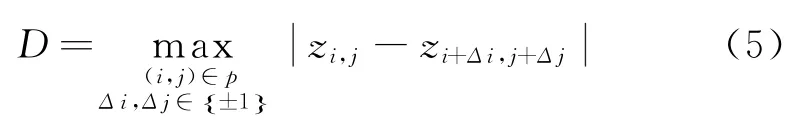
式中:p表示除最外圈栅格外的当前地块栅格集合。

2.2 地形危险度评估

目前星球巡视器大多采用轮式结构,星球表面地形对轮式巡视器移动主要造成斜坡、颠簸、台阶三种危险。其中,斜坡超过巡视器爬坡能力,容易造成车体倾覆;颠簸主要造成巡视器姿态大幅度变化,容易与星球表面发生碰撞,且降低车轮之间的协调性,甚至将其陷住;台阶是星球表面上的突起或深坑,容易造成车体与星球表面碰撞甚至被卡住。

1)斜坡

斜坡危险度定义为

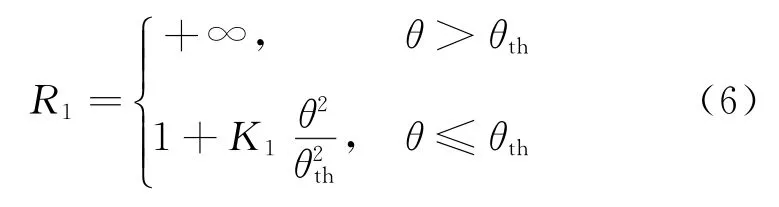
式中:θth为巡视器允许的最大爬坡能力;K1为加权系数。

2)颠簸

巡视器行驶在粗糙度为r的地块上的危险度为

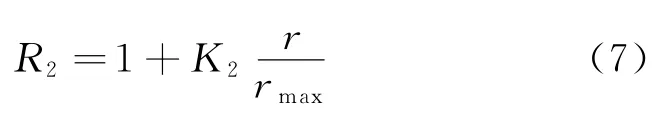
式中:rmax为所有栅格粗糙度的最大值;K2为加权系数。

(3)台阶

巡视器行驶在起伏度为D的地块上的危险度为

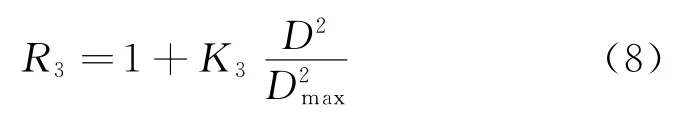
式中:Dmax为所有栅格起伏度的最大值;K3为加权系数。

为统一尺度便于比较,取K1=K2=K3=4,将这三种障碍危险度均正规化到[1,5]之间。那么,地形危险度定义为

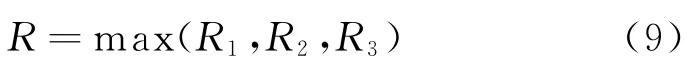
值得一提的是,尽管危险度是以地块为单位进行计算的,但它仅被赋予该地块的中心栅格,而不是整个地块。也就是说,每一个栅格(xi,yi)都有其对应的滑动分析窗口和相应地形危险度R(xi,yi),如图1所示。

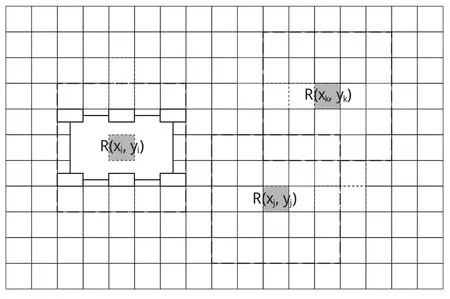
图1 地块划分及相应的地形危险度Fig.1 Patch division and related terrain risk

2.3 估价函数的选取

Risk Theta*的算法流程与Basic Theta*相同,但在估价函数中引入了地形危险度。与A*、Basic Theta*类似,Risk Theta*的估价函数为

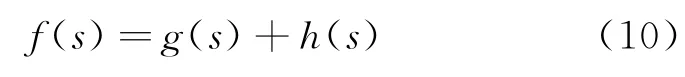
式中:g(s)为从起点s0到当前点s的实际代价函数; h(s)为从s到目标点sgoal的启发函数。

c(s,s′)取为从s到s′的连线所途经栅格(即图2中灰色栅格)的危险度的加权和。

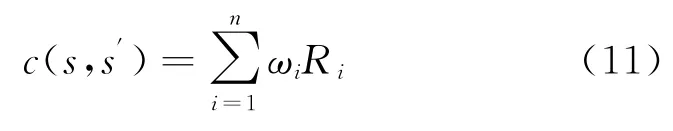
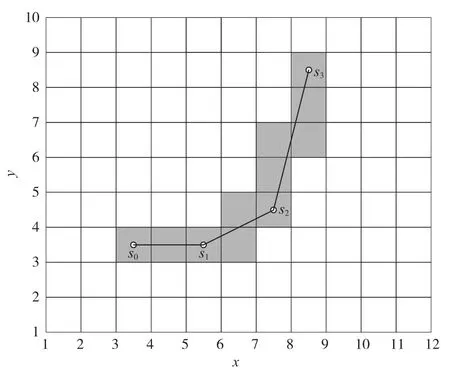
图2 代价函数计算Fig.2 Calculation of cost function

式中:Ri为途经的第i个栅格的地形危险度;ωi为相应权重。若连线在某个栅格的进出点分别位于栅格的两条对边上,如图2中栅格(4,3)、(7,5)和(8, 7)的情形,则ωi取1,否则取1/2。

c(s,s′)的具体计算借鉴了Bresenham画线算法[6]的思路,采用大量逻辑和整数操作,计算速度很快。例如,图2中的分别为

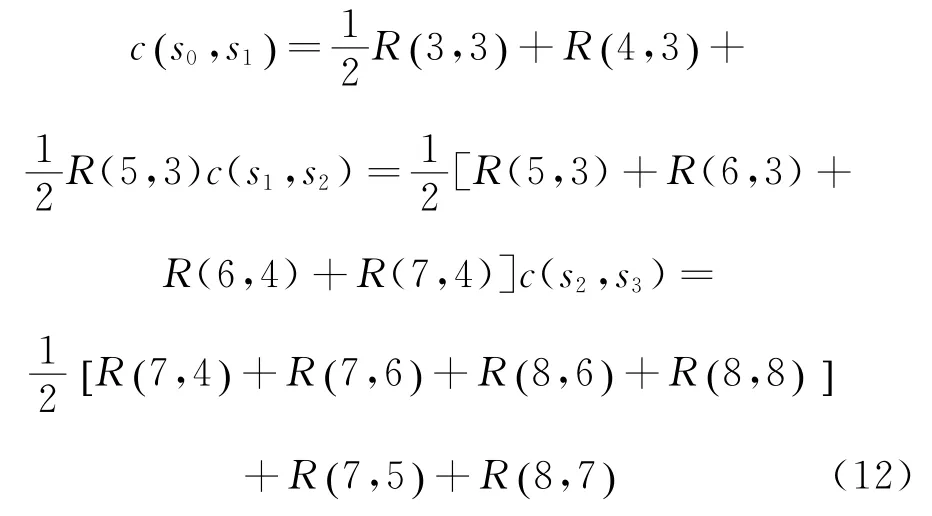
g(s)为从s0到s的各段实际路径的代价函数和。

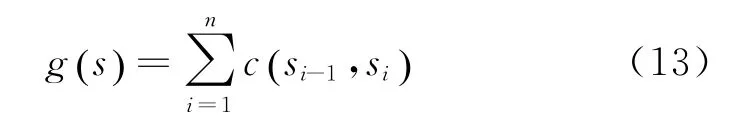
为保证可纳性(admissible),h(s)取为从s到sgoal的欧氏距离与最小危险度的乘积。

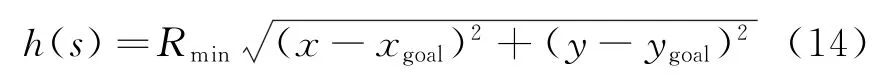
式中:Rmin是所有栅格的最小危险度,很显然Rmin=1。

3 仿真实验

本文在matlab7.0环境下对A*、Basic Theta *和Risk Theta*算法进行比对实验。参考张伍等提出的直径随机生成方法[7],生成尺寸50 m× 50 m、分辨率20 cm、网格数250×250的模拟月面DEM图,如图3所示。在此基础上根据前文所述方法生成地形危险度地图,如图4的背景图所示。

参考我国首个月面巡视器“玉兔号”设定仿真用巡视器模型的参数[8,9]:收拢状态包络尺寸为1.5 m×1.0 m×1.1 m,车轮直径30 cm,最大爬坡能力20°,越障能力20 cm。将每7×7个栅格拟合成1.4 m×1.4 m、与车体尺寸相当的地块。

在非障碍区域中随机设置起始点和目标点,分别采用A*算法、Basic Theta*算法与本文提出的Risk Theta*算法进行10次仿真实验,三种算法的仿真实验结果比较见表1,单次仿真结果路径见图4。其中,Risk Theta*的路径总危险度比A*平均减小了37.0%,路径总长度平均仅增加10.1%;路径总危险度比Basic Theta*平均减小了30.4%,路径总长度平均仅增加15.9%。特别地,Risk Theta*在单位长度上的危险度比A*和Basic Theta*分别平均减小42.2%、39.5%。

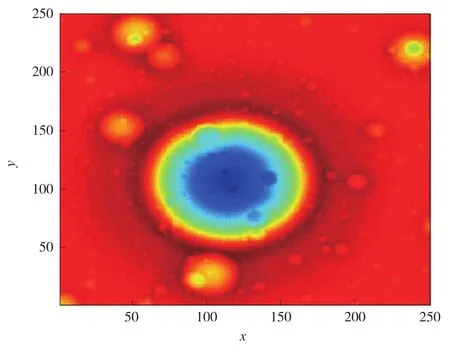
图3 模拟月面DEMFig.3 Simulated DEM of lunar surface

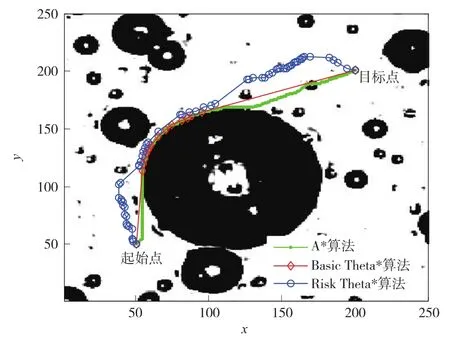
图4 A*、Basic Theta*与Risk Theta*算法的单次仿真结果Fig.4 Single simulation results of A*,Basic Theta*and Risk Theta*algorithms

从仿真结果可以看出,Risk Theta*算法得到路径的长度比A*和Basic Theta*虽略有增加,但总危险度和在每一个栅格上的危险度大大减小,因此要安全得多。

4 结 论

本文提出的Risk Theta*算法,以星球表面地形特征统计分析为基础提出了地形危险度指标,建立了地形危险度地图,并以危险度最低为方向搜索任意航向路径,能够有效解决星球表面复杂地形环境中基于二值障碍判断的Theta*算法路径解安全性较差的问题。仿真实验证明,该算法能够在栅格地图上找到比A*和Theta*算法危险度低得多、长度相当的任意航向路径,既显著提高了巡视器的安全性,又满足了星球表面巡视对任意航向行驶的迫切需求,因此具有较强的实用性。

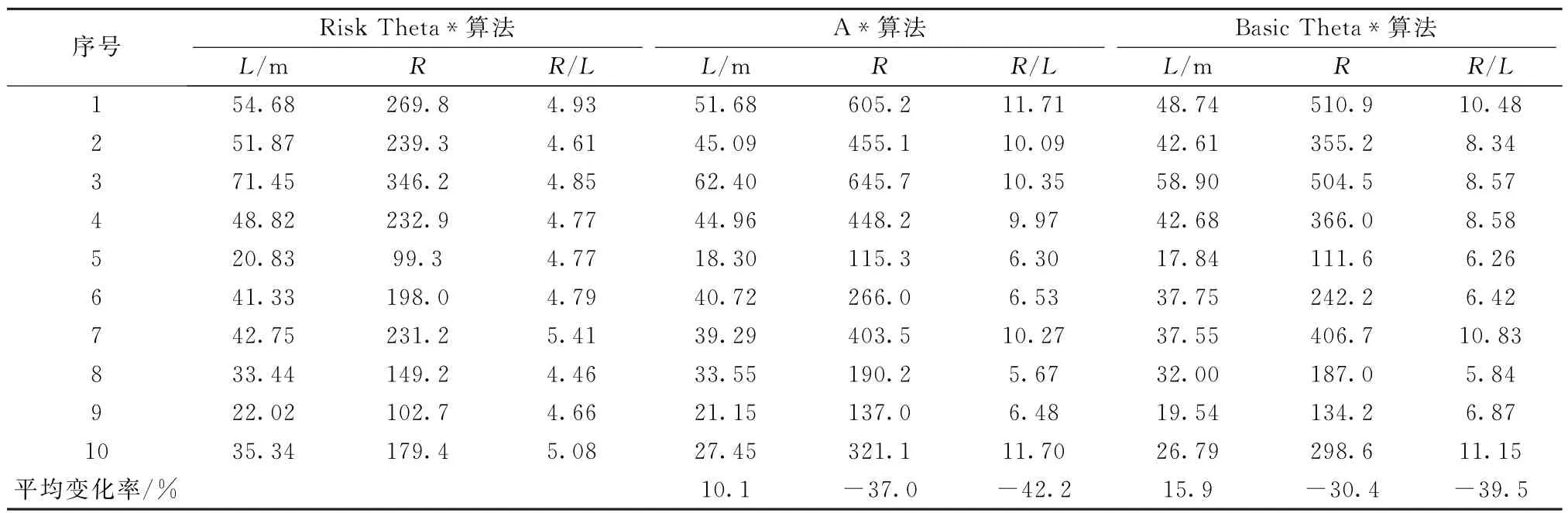
表1 A*、Basic Theta*和Risk Theta*算法的仿真结果比较Table 1 Comparison among simulation results of A*,Basic Theta*and Risk Theta*algorithms

[1]Thorpe C.Path relaxation:path planning for a mobile robot [C]∥The 4th National Conference on Artificial Intelligence. Austin,Texas,USA:[s.n.]:1984.

[2]Ferguson D,Stentz A.Field D*:an interpolation-based path planner and replanner[C]∥The 12th International Symposium of Robotics Research.San Francisco,California, USA:[s.n.]:2005.

[3]Yap P,Burch N,Holte R,et al.Block A*:database-driven search with applications in any-angle path-planning[C]//The 25th AAAI Conference on Artificial Intelligence.San Francisco,California,USA:[s.n.],2011.

[4]Nash A,Daniel K,Koenig S,et al.Theta*:Any-angle path planning on grids[C]∥The 22nd AAAI Conference on Artificial Intelligence.Vancouver,Canada:[s.n.],2007.

[5]Bresenham J.Algorithm for computer control of a digital plotter[J].IBM Systems Journal,1965,4(1):25-30.

[6]汤国安,李发源,刘学军.数字高程模型教程(第二版)[M].北京:科学出版社,2010.[Tang G A,Li F Y,Liu X J.A course in digital elevation model(2nd edition)[M].Beijing: Science Press,2010.]

[7]张伍,党兆龙,贾阳.月面数字地形构造方法研究[J].航天器环境工程,2008,25(4):35-40.[Zhang W,Dang Z L,Jia Y.Research on digital lunar terrain construction[J]. Spacecraft Environment Engineering,2008,25(4):35-40.]

[8]Sun Z Z,Jia Y,Zhang H.Technological advancements and promotion roles of Chang'e-3 lunar probe mission[J].Sci China Tech Sci,2013,56(11):2702-2708.

[9]贾阳,张建利,李群智,等.嫦娥三号巡视器遥操作系统设计与实现[J].中国科学:技术科学,2014,44(5):470-482.[Jia Y,Zhang J L,Li Q Z,et al.Design and realization for teleoperation system of the Chang'E-3 rover[J].Sci Sin Tech,2014,44(5):470-482.]

通信地址:北京市西城区车公庄大街12号核建大厦10层(100037)

电话:(010)88306151

E-mail:wangq2006@163.com

[责任编辑:高莎]

Risk Theta*:an Any-Angle Path Planning Algorithm based on Terrain Risk

WANG Qiong1,2,YU Dengyun3,JIA Yang2
(1.Lunar Exploration and Space Engineering Center,Beijing 100037,China; 2.Beijing Institute of Spacecraft System Engineering,Beijing 100094,China; 3.China Aerospace Science and Technology Corporation,Beijing 100048,China)

Risk Theta*:an any-angle path planning algorithm based on terrain risk is proposed in this paper. At first,based on statistical analysis on terrain feature of planetary surface,terrain risk index is proposed and the index map is built.Basic Theta*search is conducted on this index map to seek optimal path of lowest terrain risk. Simulation experiments show that the proposed algorithm could find out any-angle path of much lower terrain risk and comparable path length on grid map than A*and Basic Theta*which can significantly improve the rover safety,as well as satisfy the urgent demand of any-angle travel of planetary roving exploration,therefore it is fairly practical.

Theta*;terrain risk;path planning;any-angle;heuristic search

TP242.6;V448.2

:A

:2095-7777(2014)04-0269-06

10.15982/j.issn.2095-7777.2014.04.004

王琼(1983—),男,高级工程师,硕士,主要研究方向为深空探测任务总体设计、星球巡视器任务规划技术。

2014-10-01

2014-11-30

国家中长期科技发展规划重大专项资助项目