强不规则天体引力场中的动力学研究进展

姜宇,宝音贺西

(1.西安卫星测控中心宇航动力学国家重点实验室,西安710043; 2.清华大学航天航空学院,北京100084)

强不规则天体引力场中的动力学研究进展

姜宇1,2,宝音贺西2

(1.西安卫星测控中心宇航动力学国家重点实验室,西安710043; 2.清华大学航天航空学院,北京100084)

小行星探测与彗星探测是深空探测的重要方面。一般来说,小行星和彗星因质量都不足以使得万有引力克服应力达到流体静力学平衡,而具有强不规则的外形。研究强不规则天体引力场中的动力学行为及其内在机制,是探测器被不规则天体捕获并对其形成近距离探测轨道的基础。从引力场模型和动力学行为两个方面综述了强不规则天体引力场中动力学的研究进展,在引力场模型的研究方面介绍了强不规则天体引力场建模的球谐函数摄动展开模型、简单特殊体模型及多面体模型的研究现状,在动力学机制的研究方面介绍了强不规则天体引力场中的周期轨道和拟周期轨道、平衡点、流形、分岔与共振以及混沌运动的研究现状,指出了这些方面研究的重点与难点。分析了强不规则体引力场中动力学的研究趋势。

强不规则天体;小行星探测;彗星探测;宇航动力学;动力学规律

0 引 言

自古以来,人类从未放弃太空探索的梦想。从神话传说中的嫦娥奔月、夸父逐日,到敦煌壁画飞天;从帝尧陶唐氏的“梦攀天而上”,到名相伊尹乘坐宇宙飞船的梦想——“伊挚将应汤命,梦乘船过日月之傍”;从屈原的《天问》,到李白的“俱怀逸兴壮思飞,欲上青天览(揽)明月”,无不寄托着人们对太空探索的不倦追求。目前,人类的太空探索早已不局限于使用绕地卫星对地球表面及地球附近的探索,而是走向了行星际空间,包括对大行星及其卫星的环绕[1-2]、观测[3]、着陆[4]、化学成分分析[57]等,对小行星的飞越[8]、成像[810]、不规则外形与引力场建模[11-12]、着陆采样[1314]、碎石堆结构分析[15-21]等,对彗核的结构与分裂分析[22-28]、对彗发形态与物质成分的分析[2931]等。

太阳系的天体除了八大行星、矮行星以及大行星的大卫星之外,绝大多数天体都是强不规则形的[3233]。其中矮行星又叫侏儒行星,是环绕太阳运行的天体中大小介于大行星和小行星之间的、质量大到行星上物质之间的万有引力足以克服应力而达到流体静力学平衡、而质量又没有大到能清除该行星轨道上的小天体的那些天体[34]。小行星与矮行星没有明确的大小界限,国际天文联合会曾经拟建议以800 km直径为小行星与矮行星的界限,但未形成最终决议,目前小行星与矮行星之间仍无统一的被广泛接受的界限。小行星[3536]可以小至几十米,大至数百千米。比小行星更小的称为流星体[37-39],流星体和小行星之间亦无明确的界限。英国皇家天文学会曾将100μm至10 m之间的天体以及50 m以下的近地天体定义为流星体,比流星体大的则为小行星,比小行星大的则为矮行星。然而也有例外,最新发现的小天体2014 HL129的直径只有约7.6 m,也被称为小行星[40]。一般直径在100 m以上的小行星能提供足够的引力使得探测器可以环绕该小行星飞行从而成为其卫星,例如阿波罗双小行星2003 SS84的直径仅有约120 m,其卫星S/2004(2003 SS84)1的直径约为60 m[4142],直径如此之小的小行星也能提供足够的引力形成双小行星系统,这是迄今为止人类发现的最小的双小行星系统。

小行星951 Gaspra[43]是人类第一次造访过的小行星,“伽利略号”探测器于1991年飞越该小行星,最近距离1 600 km。小行星951 Gaspra的尺寸为18.2×10.5×8.9 km[44],具有强不规则的外形[45],其轨道半长轴为2.6 AU,逃逸速度为6 m/s,一个Gaspra天为7.042 h。人类第一次发现的双小行星系统是Ida-Dactyl系统[46]。1993年“伽利略号”探测器[4748]飞越了小行星243 Ida,最近距离2 400 km。小行星243 Ida[47-51]的轨道半长轴为2.991 AU,尺寸为53.6×24.0×15.2 km,其小月亮Dactyl的尺寸为1.6×1.4×1.2 km,可见该双小行星系统是由两个强不规则天体组成,两个小行星的距离为90 km,一个Ida天为4.63 h,小月亮Dactyl的公转周期约20 h[47,49,52]。除了对小行星等太阳系强不规则小天体进行飞越观测之外,还要进行表面登陆及采样返回[14,53]。其中,“隼鸟号”是人类第一个对小行星进行采样返回的探测器[8,13-15]。“罗塞塔号”是人类第一个对彗星核进行登陆的探测器,已于2014年11月登陆彗星67P/Churyumov-Gerasimenko[54-56]。

1 引力场模型研究现状

人们对天体引力场建模方法的研究,经历了从简单到复杂、从低维到高维的研究阶段[57-69]。经典的引力场建模方法是对球谐函数叠加摄动项并进行级数展开,一个均质球的引力场等效于一个点质量产生的引力场,点是测度为零的零维对象,因此球谐函数摄动展开方法是在一个测度为零的对象上进行摄动处理[57-59]。对于地球、火星等近球形天体,由于级数收敛较快,球谐函数摄动展开方法的效果良好[57,70]。而对于小行星951 Gaspra[43-44]、216 Kleopatra[7175]与1620 Geographos[7678]等强不规则天体[7995]来说,在小行星附近的一些区域上,级数发散,在另外一些区域上,级数收敛速度非常慢[96-109]。因此,探索能有效解决这一难题的引力场建模方法成为太阳系小天体几何形状与物理特性研究领域的重要内容[68-69,96-99]。此后,质点群模型[110]与简单特殊体模型[60-67]被用来尝试克服这一难题。其中,质点群模型对强不规则天体的建模精确程度远好于球谐函数摄动展开模型,但质点群模型计算量较大,从测度论的意义上讲,质点群模型的有限个质点的测度仍然为零,也是零维的物体[110]。此后由Werner于1994年建立的小行星多面体模型法[68]不仅能克服处理球谐函数摄动展开模型在特殊区域发散的问题,还能仿真出强不规则天体的几何外形与质量瘤[68-69,111],目前已经能采用成千上万个点与面来对强不规则天体进行几何与物理建模[112-127]。此外多面体是三维的物体,其测度不为零[112,123,126]。特别是对于双小行星系统,多面体模型法是目前唯一能同时解决收敛与强不规则几何外形仿真的方法[128-130]。

1.1 球谐函数摄动展开模型

将探测器看作一个质点,考虑该质点在小行星等强不规则天体引力场中的运动。如果质点距离强不规则天体足够远,则该天体的引力场可近似看作一个均值圆球产生的引力场,或者说近似看作一个质点产生的引力场,因为均值圆球的引力场等效于一个质点产生的引力场,此时,需要考虑太阳引力对质点运动的影响。倘若该天体的外形接近球形,例如地球、火星等,则经典的Legendre级数方法可以用来近似其引力场[57-59];并且天体的外形越接近球形,则级数的收敛速度越快[131-132]。Hu和Scheeres (2002,2004)[133-134]采用Legendre级数展开的2阶项来近似匀速自旋天体的引力场,并分析了考虑2阶项时的轨道运动的稳定区域。如果天体的形状是不规则的,则天体附近Legendre级数难以收敛[101,131-132],在一些点或区域上,Legendre级数还会发散[61,63-64]。

1.2 简单特殊体模型

在强不规则天体附近动力学行为研究的早期,人们通过研究简单特殊体附近的动力学行为来帮助理解一般强不规则天体引力场中的可能运动状态。这些简单特殊体包括细直棒[63,66,98100,103,131-132]、圆环[60,64,106]、圆饼[62,65,102]、三角盘与正方形盘[101]、立方体[67,104-105,107]、哑铃体[108]等。

细直棒是一维的物体,具有良好的对称性,仅用一维坐标就可以表示细直棒上的点,然而研究表明,其附近的动力学行为异常复杂,棒体之外有4个平衡点,大范围轨道和平衡点周围的局部轨道均存在共振与混沌的现象[66,99,103]。Elipe和Riaguas (2003)[63]研究了旋转细直棒所产生的对数形式引力场中的有效势与平衡点。Elipe和Lara(2003)[99]将小行星433 Eros的物理模型简化为细直棒,并考虑细直棒产生的引力场中的平衡点、周期轨道族以及分岔行为。Lindner等(2010)[103]发现细直棒附近存在稳定的同步轨道、一般的混沌轨道、不稳定周期轨道、旋转稳定轨道等。Najid等(2011)[66]通过计算Poincaré截面展示了细直棒附近的复杂动力学行为。三角盘、正方形盘、圆环以及圆饼都是二维的物体,也具有良好的对称性,用两维坐标系可以表示该物体上的点。通过绘制Poincaré截面知,三角盘和正方形盘引力场中都存在周期轨道,其Poincaré截面上存在不动点和孤岛[101]。

1.3 多面体模型

通常的引力多体问题,考虑多个质点在相互之间的引力作用下的运动,属于有限个点质量产生的引力场,其测度仍然为零;若将有限个点增加到可数无穷个点,乃至连通的不可数无穷个点形成的点集,研究其引力场中的运动,就要考虑一般的非零测集的三维空间的强不规则天体引力场中的动力学机制。Werner(1994)[68]给出了使用均质多面体描述不规则小天体几何外形与引力场物理模型的方法,并将该方法应用到模拟火卫一的几何外形与引力场物理模型中,使用了146个顶点和288个三角形面。Scheeres等(1996)[112]使用小行星4769 Castalia的由雷达观测数据生成的多面体物理模型,研究了小行星附近的质点运动,给出并讨论了质点运动的Jacobi积分与零速度面的表达形式,并计算了若干个周期轨道族。Werner和Scheeres(1997)[69]进一步详细推导了常密度多面体外部引力的解析表达,包括引力势、引力、引力梯度矩阵等,并将其应用到小行星4769 Castalia的几何外形与引力物理模型的建立之中,给出了应用多面体处理小行星4769 Castalia质量瘤的方法。

将多面体模型同球谐函数模型和简单特殊体模型相比,球谐函数建模[57-59,131-134]方法是在一个点质量的基础上叠加摄动来近似天体,点质量的测度为零,不能描述天体的不规则性,且球谐函数方法不能解决一些区域级数发散的问题[61,63-64]。简单特殊体模型[60-67,98-108,131-132]只能用来作为对不规则天体引力场中动力学行为的初步探索和理解使用,不存在任何一个小行星是一维的细直棒、平面盘或者立方体等简单特殊体形状[63-64,68-69]。因此,自从Werner给出了使用多面体描述不规则小行星几何外形与引力场物理模型的方法[68]之后,多面体模型已经在小天体附近动力学的研究中成为最为先进的方法[69,109-127]。此后采用多面体模型对小天体进行建模并研究其引力场中的动力学行为的包括小行星4179 Toutatis[113]、433 Eros[114]、216 Kleopatra[120-125]、2002 AT 4[118]、1989 ML[118]、1620 Geographos[123-124],以及小行星4769 Castalia[123]和6489 Golevka[123]。

2 动力学机制研究现状

截至2014年4月16日,已发现的太阳系中的小行星共有1 111 087个[135],能使用受摄开普勒轨道理论或平面圆型限制性三体问题理论研究探测器在其引力场中运动的天体只有几十个,这些天体以外形非常接近圆球的太阳和大行星及大行星的大卫星为主[96-99,120-124]。太阳系的绝大多数天体都具有复杂的强不规则外形,经典的轨道理论适用于描述近球形天体所产生的引力场中的探测器运动,而不适用于这些强不规则天体[9499]。此外,受摄开普勒轨道理论依赖于球谐函数的引力场模型[57-59]。能否发展新的理论研究,适用于任何引力场模型,包括球谐函数模型、其他特殊函数模型、特殊外形模型、质点群模型、多面体模型等,则需研究能描述强不规则天体引力场中探测器运动的理论,适用于所有旋转强不规则天体引力场中的探测器运动,且新的理论研究不依赖于任何具体的引力场模型,而是广泛适用于任何引力场模型。

作为共性基础理论研究,开展强不规则引力场中动力学的研究,也有助于星系动力学[60,62,102,136-145]、天体力学[96-108,146149]、宇航动力学[109-124]以及行星地质动力学[11-13,150-151]、天体物理散体动力学[13,21,152-153]、天体物理流体动力学[154-155]等学科研究的进步。一般来说,小行星和彗核大都具有强不规则的外形[8-9,12,17]。目前已经被作为研究对象来分析其附近动力学行为的太阳系的强不规则小天体包括:火卫一[68]、小行星4 Vesta[119]、216 Kleopatra[120-125]、433 Eros[114-115,118,126]、1580 Betulia[118]、1620 Geographos[123]、4179 Toutatis[113,118]、4769 Castalia[69,109,112,123]、6489 Golevka[123]、25143 Itokawa[116-117]以及彗星67/ P CG[118]。

不规则天体附近的运动稳定性需要考虑Jacobi积分与零速度面,其中零速度面将空间区域分为质点运动的禁区与可行区域[112,118,120-121,123-124]。平衡点的稳定性完全决定了平衡点附近质点的运动稳定性[99,123]。存在一个度量,在该度量下质点相对强不规则体的轨道是流形在等能量超曲面上赋予了该度量的测地线,反之,流形在等能量超曲面上赋予了该度量的测地线是质点相对强不规则体的轨道[123]。下面从平衡点的存在性、个数与稳定性,周期轨道族的存在性,流形与子空间结构、分岔、共振、混沌等几个方面来介绍国际上相关领域的研究进展。

2.1 周期轨道和拟周期轨道

旋转不规则天体引力场附近存在周期轨道,这种周期轨道的几何形状可能非常复杂[96,101,112113,118,121,123]。这些周期轨道可以通过不同的方式进行分类[112,121,123]。根据周期轨道的直观几何形状,Scheere等[112]以小行星4769 Castalia为例,将其附近的周期轨道分为三类,包括准赤道顺行(quasi-equatorial direct)周期轨道、准赤道逆行(quasi-equatorial retrograde)周期轨道以及非赤道(nonequatorial)周期轨道。Broucke和Elipe (2005)[64]依据轨道的对称性与直观几何外形,将巨形环引力场中的周期轨道分为10种类型。周期轨道族的寻找是非常复杂的,在2013年以前,人类只找到了三质点体问题的三族周期轨道,Lagrange-Euler族、Broucke-Hénon族以及Moore等于1993年发现的图-8族(figure-eight family)[146-147]。Šuvakov和Dmitrašinovi于2013年找到了三体问题的13族新的周期解[148],发表在物理学领域顶尖杂志Phys.Rev.Lett.上,Science杂志以新闻报道的方式抢先披露了这一研究进展(Jon Cartwright[149])。如果天体从质点变为一般的强不规则体,则情况更为复杂。Yu和Baoyin(2012)[121]提出一种周期轨道分层网格搜索算法并以该算法为分类原则,找出小行星216 Kleopatra附近的29族周期轨道。Riaguas等(1999)[96]找到了细直棒引力场中的多组具有不同稳定特性的周期轨道。Jiang等(2014)[123]依据平衡点附近流形的拓扑结构将平衡点附近的周期轨道分为不同的拓扑类型,对于有的拓扑情形的平衡点的附近还存在拟周期轨道,图1给出了小行星216 Kleopatra的一个平衡点附近的拟周期轨道,该轨道属于二维环面上的拟周期轨道。

通过周期轨道的延拓[121,123]可以由1条周期轨道得到相同拓扑特性的无穷多条周期轨道。如果将可以延拓得到的周期轨道族中的所有周期轨道捏成1条周期轨道,则开普勒二体问题仅有1条周期轨道,限制性三体问题的单个平衡点附近最多有3条周期轨道,日地系统5个平衡点附近共有12条局部周期轨道,而在小行星6489 Golevka附近的局部周期轨道共有10条[123]。

2.2 平衡点

针对简单特殊体引力场中平衡点的存在性、个数与稳定性,有若干颇有意思的研究成果。Elipe和Riaguas(2003)[63]找到了旋转对数函数引力场及旋转有限长细直棒引力场中的4个外部平衡点,并且讨论了这4个平衡点的稳定性。Scheeres等(2004)[116-117]发现了小行星25143 Itokawa引力场中的4个外部平衡点并给出了它们在小行星本体坐标系的坐标位置。Mondelo等(2010)[119]发现了小行星4 Vesta引力场中的4个外部平衡点,并且给出了它们的坐标及稳定性;他们的研究表明其中2个平衡点是稳定的,另外2个是不稳定的。Yu和Baoyin(2012)[120]发现了小行星216 Kleopatra引力场中的4个外部平衡点并给出了这些平衡点的位置坐标、特征值与线性稳定性,发现这4个平衡点附近存在6族不同的周期轨道。Scheeres(2012)[118]发现了小行星1580 Betulia引力场中的6个外部平衡点以及彗星67P/CG引力场中的4个外部平衡点。

图1 小行星216 Kleopatra的一个平衡点附近的拟周期轨道[123]Fig.1 A quasi-periodic orbit near an equilibrium point in the potential field of the asteroid 216 Kleopatra[123]

Jiang等(2014)[123]建立了一般的旋转小行星平衡点附近的运动理论,包括平衡点附近线性化的运动方程、特征方程,平衡点稳定的一个充分条件、一个充分必要条件,以及非退化平衡点的拓扑分类和子流形结构;此外,将旋转不规则天体引力场中的非退化平衡点分为8种可能的拓扑类型,其中非退化并且非共振的平衡点有5种拓扑类型,而非退化并且共振的平衡点有3种拓扑类型。非退化并且非共振的平衡点的拓扑类型如表1所示[123]。Wang等(2014)[127]计算了23个有精确外形模型的强不规则天体的平衡点的个数及拓扑类型与稳定性,其中15个小行星、5个大行星的卫星、3个彗核;发现这23个天体均存在内部平衡点,除小行星216 Kleopatra有3个内部平衡点外,其余天体均只有1个内部平衡点;发现除了小行星1998 KY26没有外部平衡点以外,其余天体均有外部平衡点,其中101955 Bennu有8个外部平衡点,其余天体均有4个外部平衡点;发现小行星4 Vesta、2867 Steins、6489 Golevka、52760,大行星的大卫星M1 Phobos、N8 Proteus、S9 Phoebe以及彗核1P/Halley和9P/ Tempel 1的每一个,均有3个平衡点的拓扑类型属于情形1;此外,发现这23个不规则天体的外部平衡点若属于情形1与情形2,则不同拓扑类型的平衡点间隔分布,属于情形1的外部平衡点个数与属于情形2的外部平衡点个数相等;同样,若这些天体的外部平衡点属于情形2与情形5,则不同拓扑类型的平衡点也间隔分布,属于情形2的外部平衡点个数与属于情形5的外部平衡点个数相等。图2和图3给出了小行星216 Kleopatra及彗核103P/ Hartley的有效势、平衡点以及平衡点的拓扑类型[123,127]。不同拓扑类型的外部平衡点间隔分布、个数相等,这一现象对所有的强不规则天体都成立,还是仅对满足某些条件的不规则天体成立,目前尚无定论,该现象的内在动力学机制需深入研究。

和平衡点有关的问题如平衡点的个数、有限性等问题远未解决,菲尔茨奖和沃尔夫奖双奖得主Smale(1998)在文献[156]中列出了21世纪的18个数学领域的世纪性问题,其中N-质点体的系统中相对平衡点个数的有限性被列为第6个世纪性问题,如果将这N个质点中的部分或全部换成强不规则体,则情况将更加复杂,此时不规则体的引力势和旋转势相互耦合。

表1 旋转不规则天体引力场中的非退化并且非共振的平衡点的5种可能的拓扑类型[123]Table 1 Five topological cases of the non-degenerate and nonresonant equilibrium points in the potential field of irregular celestial bodies[123]

2.3 流形

《彖》曰:“大哉乾元、万物资始,乃统天。云行雨施,品物流形。”流形是旋转强不规则体引力场中动力学研究的一个重要方面,其中平衡点附近的流形可以分为渐近稳定流形、渐近不稳定流形以及中心流形,这些流形分别同渐近稳定子空间、渐近不稳定子空间以及中心子空间在平衡点处相切[104,119-120,123]。Mondelo等(2010)[119]讨论了小行星4 Vesta平衡点附近的周期轨道与对应的流形。Liu等(2011)[104]考虑了旋转均质立方体引力场中平衡点附近的流形结构,给出了渐近稳定流形与渐近不稳定流形在位置空间的投影,进一步计算了不同平衡点之间的异宿轨道。Yu和Baoyin (2012)[120]以小行星216 Kleopatra为研究对象,计算了在单参数变化下,渐近稳定流形、渐近不稳定流形以及中心流形在位置空间的投影和每一个平衡点附近周期轨道族周期的取值区间。Jiang等(2014)[123]发现了一般的旋转简单形状体或强不规则体的非退化平衡点的8种可能的拓扑类型对应的流形结构,包括线性稳定类型1种、不稳定兼非共振类型4种、以及共振类型3种,并将理论结果应用到小行星216 Kleopatra、1620 Geographos、4769 Castalia和6489 Golevka中。

图2 小行星216Kelopatra及彗核103P/Hartley 2的有效势[127]Fig.2 The effective potential of the asteroid 216 Kleopatra and the comet 103P/Hartley 2[127]

图3 小行星216Kelopatra及彗核103P/Hartley的平衡点及其拓扑类型[123,127](圆点表示属于拓扑情形1对应的平衡点,星形表示拓扑情形2对应的平衡点,三角形表示拓扑情形5对应的平衡点)Fig.3 The topological cases of the equilibrium points for the asteroid 216 Kleopatra and the comet 103P/Hartley 2[123,127](Dot:Case 1,Star:Case 2;Triangle:Case 5)

2.4 分岔与共振

在强不规则体的质量分布、几何外形、自旋速度以及运动质点的Jacobi积分等参数变化下,运动可能表现出分岔行为。Riaguas等(1999)[96]发现了细直棒引力场参数变化下周期轨道的分岔行为。Galán等(2002)[147]分析了三体问题图-8解的分岔行为。此外,共振平衡点附近也可能会出现分岔[123]。

共振有多种可能的类型:Scheeres等(1996)[112]考虑使用球谐函数模型来对小行星4769 Castalia的引力场进行建模,并分析了2阶引力场解析近似引起的运动质点轨道角速度与小行星自旋角速度成整数比1∶1及2∶3引起的共振行为。Scheeres等(2000)[114]进一步对小行星433Eros使用2阶球谐函数引力场近似分析了3∶2、2∶1及1∶2共振。Yu和Baoyin(2013年)[122]从质点机械能是否突变的角度来考虑,发现并分析了小行星附近质点运动的瞬时共振行为。此外,质点轨道角速度与小行星自旋角速度成1∶1的共振轨道同小行星的平衡点重合[119,123]。此外,在惯性空间来看,旋转强不规则天体的平衡点是天体旋转角速度与质点轨道角速度之比为1∶1共振的轨道,Jiang等(2014)[123]发现的共振平衡点是双重的共振,包含天体旋转角速度与质点轨道角速度之比为1∶1的共振以及平衡点的纯虚特征值数值之比为1∶1的共振。

2.5 混沌

混沌与分岔及共振紧密相连,若干关于简单特殊体引力场的研究表明,其中质点的运动可能表现出混沌行为[99,103,105]。Elipe和Lara(2003)[99]讨论了细直棒引力场中的1∶1共振引起的分岔,发现在参数变化下,共振将导致混沌的产生。Lindner等(2010)[103]发现了绕旋转巨形细直棒公转的质点运动的混沌行为,质点的运动包括稳定同步轨道、一般混沌轨道以及不稳定周期轨道和自旋稳定轨道族。Poincaré截面是一个有效的工具,通过它不仅可以观察周期轨道的存在性,还能有助于分析质点运动的混沌行为[64,66,101,105]。Broucke和Elipe(2005)[64]通过计算固体圆环引力场中的Poincaré截面,如图4所示,发现截面上存在的显著孤岛点,对应着环绕着该圆环的周期轨道。Blesa(2006)[101]分别计算了平面三角盘及正方形盘引力场中的Poincaré截面,找到了若干条周期轨道。Najid等(2011)[66]计算了细直棒引力场中的若干Poincaré截面,展现了其中动力学行为整体结构的一个概览。Liu等(2011)[105]通过计算Poincaré截面找出了旋转立方体引力场中的周期轨道。

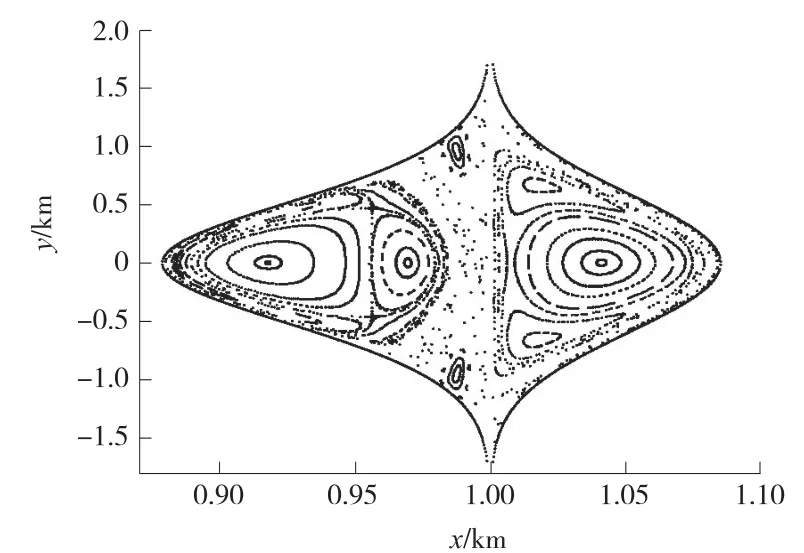
图4 固体圆环引力场中的Poincaré截面[64]Fig.4 Poincarésurface of sections in the potential field of a solid ring

3 结束语

预计未来强不规则体引力场中动力学的研究趋势为:

1)更加注重理论研究的普适性[123-124]。此前,关于受摄二体问题轨道理论研究中,有通过J2项得出的太阳同步轨道和临界轨道等,相关的理论结果依赖于球谐函数摄动展开模型。目前关于强不规则天体引力场的建模已有多种方法,未来动力学行为的研究预计将朝着不依赖于具体的建模方法的方向发展,而是针对一般情况,适用于任何关于强不规则天体引力场的建模方法,包括球谐函数展开、简单特殊体、多面体等[123124]。

2)研究成果的一般性增强[123]。Kepler二体问题可以看作是限制性三体问题的特例,而使用无质量细长杆将限制性三体问题的两个天体连接,则可以看作是一个特殊的强不规则天体,因此限制性三体问题是平面对称体引力场的特例,而平面对称体又是一般的强不规则天体的特例。因此,针对一般的强不规则天体引力场中轨道运动的研究结论,将适用于简单特殊体和限制性三体等特例情形[123]。

3)从关注解析性质和外在几何性质到关注内在几何性质、拓扑性质乃至代数性质的转变[123,127]。经典的受摄二体问题轨道理论关注轨道根数的变化率等解析性质以及轨道的几何外形等外在的几何性质。经典的限制性三体问题理论和受摄限制性三体问题理论关注局部性质和解析性质。强不规则天体引力场中的轨道运动则更关注轨道的流形结构等几何性质、平衡点及轨道的种类等拓扑性质等[123-124,127]。

[1]Smith B A,Soderblom L,Beebe R,et al.Encounter with Saturn:Voyager 1 imaging science results[J].Science, 1981,212(4491):163-191.

[2]Broadfoot A L,Sandel B R,Shemansky D E,et al.Extreme ultraviolet observations from Voyager 1 encounter with Saturn[J].Science,1981,212(4491):206-211.

[3]Bish D L,Blake D F,Vaniman D T,et al.X-ray diffraction results from Mars Science Laboratory:mineralogy of Rocknest at Gale crater[J].Science,2013,341 (6153):1238932.

[4]Blake D F,Morris R V,Kocurek G,et al.Curiosity at Gale crater,Mars:characterization and analysis of the Rocknest sand shadow[J].Science,2013,341(6153):1239505.

[5]Meslin P Y,Gasnault O,Forni O,et al.Soil diversity and hydration as observed by ChemCam at Gale Crater,Mars [J].Science,2013,341(6153):1238670.

[6]Vaniman D T,Bish D L,Ming D W,et al.Mineralogy of a mudstone at Yellowknife Bay,Gale crater,Mars[J]. Science,2014,343(6169):1243480.

[7]Walsh K J,Morbidelli A,Raymond S N,et al.A low mass for Mars from Jupiter's early gas-driven migration[J]. Nature,2011,475(7355):206-209.

[8]Saito J,Miyamoto H,Nakamura R,et al.Detailed images of asteroid 25143 Itokawa from Hayabusa[J].Science,2006, 312(5778):1341-1344.

[9]Jewitt D,Weaver H,Agarwal J.A recent disruption of the main-belt asteroid P/2010 A2[J].Nature,2010,467(7317): 817-819.

[10]NesvornýD,Bottke Jr W F,Dones L,et al.The recent breakup of an asteroid in the main-belt region[J].Nature, 2002,417(6890):720-771.

[11]Zuber M T,Smith D E,Cheng A F,et al.The shape of 433 Eros from the NEAR-Shoemaker laser rangefinder[J]. Science,2000,289(5487):2097-2101.

[12]Scheeres D J,Fahnestock E G,Ostro S J,et al.Dynamical configuration of binary near-Earth asteroid(66391)1999 KW4[J].Science,2006,314(5803):1280-1283.

[13]Tsuchiyama A,Uesugi M,Matsushima T,et al.Threedimensional structure of Hayabusa samples:origin and evolution of Itokawa regolith[J].Science,2011,333(6046): 1125-1128.

[14]Yurimoto H,Abe K I,Abe M,et al.Oxygen isotopic compositions of asteroidal materials returned from Itokawa by the Hayabusa mission[J].Science,2011,333(6046): 1116-1119.

[15]Yano H,Kubota T,Miyamoto H,et al.Touchdown of the Hayabusa spacecraft at the Muses Sea on Itokawa[J]. Science,2006,312(5778):1350-1353.

[16]Trieloff M,Jessberger E K,Herrwerth I,et al.Structure and thermal history of the H-chondrite parent asteroid revealed by thermochronometry[J].Nature,2003,422 (6931):502-506.

[17]Jutzi M,Asphaug E,Gillet P,et al.The structure of the asteroid 4 Vesta as revealed by models of planet-scale collisions[J].Nature,2013,494(7436):207-210.

[18]Walsh K J,Richardson D C,Michel P.Rotational breakup as the origin of small binary asteroids[J].Nature,2008,454 (7201):188-191.

[19]Vernazza P,Binzel R P,Rossi A,et al.Solar wind as the origin of rapid reddening of asteroid surfaces[J].Nature, 2009,458(7241):993-995.

[20]Thomas P C,Veverka J,Robinson M S,et al.Shoemaker crater as the source of most ejecta blocks on the asteroid 433 Eros[J].Nature,2001,413(6854):394-396.

[21]Walsh K J,Richardson D C,Michel P.Rotational breakup as the origin of small binary asteroids[J].Nature,2008,454 (7201):188-191.

[22]Farnham T L,Schleicher D G,Woodney L M,et al. Imaging and photometry of comet C/1999 S4(LINEAR) before perihelion and after breakup[J].Science,2001, 292(5520):1348-1353.

[23]Hsieh H H,Jewitt D.A population of comets in the main asteroid belt[J].Science,2006,312(5773):561-563.

[24]Snodgrass C,Tubiana C,Vincent J B,et al.A collision in 2009 as the origin of the debris trail of asteroid P/2010 A2[J].Nature,2010,467(7317):814-816.

[25]Küppers M,Bertini I,Fornasier S,et al.A large dust/ice ratio in the nucleus of comet 9P/Tempel 1[J].Nature, 2005,437(7061):987-990.

[26]Martins Z,Price M C,Goldman N,et al.Shock synthesis of amino acids from impacting cometary and icy planet surface analogues[J].Nature Geoscience,2013(6):1045-1049.

[27]Sunshine J M,A'Hearn M F,Groussin O,et al.Exposed water ice deposits on the surface of comet 9P/Tempel 1[J]. Science,2006,311(5766):1453-1455.

[28]Zolensky M E,Zega T J,Yano H,et al.Mineralogy and petrology of comet 81P/Wild 2 nucleus samples[J].Science, 2006,314(5806):1735-1739.

[29]Nuth J A,Hill H G,Kletetschka G.Determining the ages of comets from the fraction of crystalline dust[J].Nature, 2000,406(6793):275-276.

[30]Ishii H A,Bradley J P,Dai Z R,et al.Comparison of comet 81P/Wild 2 dust with interplanetary dust from comets[J]. Science,2008,319(5862):447-450.

[31]Gloeckler G,Geiss J,Schwadron N A,et al.Interception of comet Hyakutake's ion tail at a distance of 500 million kilometres[J].Nature,2000,404(6778):576-578.

[32]Abe S,Mukai T,Hirata N,et al.Mass and local topography measurements of Itokawa by Hayabusa[J].Science,2006, 312(5778):1344-1347.

[33]Soderblom L A,Becker T L,Bennett G,et al.Observations of comet 19P/Borrelly by the miniature integrated camera and spectrometer aboard Deep Space 1[J].Science,2002, 296(5570):1087-1091.

[34]Brown M E,Schaller E L.The mass of dwarf planet Eris [J].Science,2007,316(5831):1585-1585.

[35]Pravec P,ŠarounováL,Wolf M.Lightcurves of 7 near-Earth asteroids[J].Icarus,1996,124(2):471-482.

[36]Ostro S J,Scott R,Nolan M C,et al.Radar observations of asteroid 216 Kleopatra[J].Science,2000,288(5467): 836-839.

[37]Yin Q,Jacobsen S B,Yamashita K,et al.A short timescale for terrestrial planet formation from Hf-W chronometry of meteorites[J].Nature,2002,418(6901):949-952.

[38]Klekociuk A R,Brown P G,Pack D W,et al.Meteoriticdust from the atmospheric disintegration of a large meteoroid [J].Nature,2005,436(7054):1132-1135.

[39]Porubˇcan V,KornošL.The Lyrid Meteor Stream:Orbit and Structure[J].Earth,Moon and Planets,2008(102): 91-94.

[40]Newly-discovered,bus-sized asteroid zips by Earth;2014 HL129 comes closer than Moon[EB/OL].[2014-07-30]. http://www.ibtimes.co.in/articles/551075/20140505/bussize-asteroid-2014-hl129-zips-earth.htm.

[42]Benner L A,Ostro S J,Magri C,et al.Near-Earth asteroid surface roughness depends on compositional class[J].Icarus, 2008,198(2):294-304.

[43]Belton M JS,Veverka J,Thomas P,et al.Galileo encounter with 951 Gaspra:First pictures of an asteroid[J].Science, 1992,257(5077):1647-1652.

[44]Thomas P C,Veverka J,Simonelli D,et al.The shape of Gaspra[J].Icarus,1994,107(1):23-36.

[45]Gaspra Approach Sequence[EB/OL].[2014-07-30].http:// www.solarviews.com/cap/ast/gaspra4.htm.

[46]Belton M J S,Chapman C R,Veverka J,et al.First images of asteroid 243 Ida[J].Science,1994,265(5178):1543-1547.

[47]Chapman C R,Veverka J,Thomas P C,et al.Discovery and physical properties of Dactyl,a satellite of asteroid 243 Ida [J].Nature,1995,374(6525):783-785.

[48]Helfenstein P,Veverka J,Thomas P C,et al.Galileo photometry of asteroid 243 Ida[J].Icarus,1996,120(1): 48-65.

[49]Geissler P,Petit J M,Durda D D,et al.Erosion and ejecta reaccretion on 243 Ida and its moon[J].Icarus,1996,120 (1):140-157.

[50]Sullivan R,Greeley R,Pappalardo R,et al.Geology of 243 Ida[J].Icarus,1996,120(1):119-139.

[51]Ida and dactyl in enhanced color[EB/OL].[2014-07-30]. http://www.solarviews.com/cap/ast/idamnclr.htm.

[52]VokrouhlickýD,NesvornýD,Bottke W F.The vector alignments of asteroid spins by thermal torques[J].Nature, 2003,425(6954):147-151.

[53]Barucci M A,Cheng A F,Michel P,et al.MarcoPolo-R near earth asteroid sample return mission[J].Experimental Astronomy,2012,33(2-3):645-684.

[54]Schulz R,Stuwe J A,Boehnhardt H.Rosetta target comet 67P/Churyumov-Gerasimenko[J].Astronomy and Astrophysics,2004,422(1):19-21.

[55]Gicquel A,Bockelée-Morvan D,Leyrat C,et al.Model of dust thermal emission of comet 67P/Churyumov-Gerasimenko for the Rosetta/MIRO instrument[J]. Planetary and Space Science,2013(85):214 219.

[56]Keller H U,Jorda L,Küppers M,et al.Deep impact observations by OSIRIS onboard the rosetta spacecraft[J]. Science,2005(310):281-283.

[57]Kozai Y.The motion of a close earth satellite[J].The Astronomical Journal,1959(64):367-377.

[58]Brouwer D.Solution of the problem of artificial satellite theory without drag[J].The Astronomical Journal,1959 (64):378.

[59]Izsak I G.A note on perturbation theory[J].The Astronomical Journal,1963(68):559-560.

[60]Lass H,Blitzer L.The gravitational potential due to uniform disks and rings[J].Celestial Mechanics,1983,30(3): 225-228.

[61]Balmino G.Gravitational potential harmonics from the shape of a homogeneous body[J].Celestial Mechanics and Dynamical Astronomy,1994,60(3):331-364.

[62]Eckhardt D H,Pestaña J L G.Technique for modeling the gravitational field of a galactic disk[J].Astrophysics Journal,2002,572(2):135-137.

[63]Elipe A,Riaguas A.Nonlinear stability under a logarithmic gravity field[J].International Mathematics Journal.2003 (3):435-453.

[64]Broucke R A,Elipe A.The dynamics of orbits in a potential field of a solid circular ring[J].Regular and Chaotic Dynamics,2005,10(2):129-143.

[65]Alberti A,Vidal C.Dynamics of a particle in a gravitational field of a homogeneous annulus disk[J].Celestial Mechanics and Dynamical Astronomy,2007,98(2):75-93.

[66]Najid N E,Elourabi E H,Zegoumou M.Potential generated by a massive inhomogeneous straight segment[J].Research in Astronomy and Astrophysics,2011,11(3):345-352.

[67]Chappell J M,Chappell M J,Iqbal A,et al.The gravity field of a cube[J].Physics International,2012(3):50-57.

[68]Werner R A.The gravitational potential of a homogeneous polyhedron or don't cut corners[J].Celestial Mechanics and Dynamical Astronomy,1994,59(3):253-278.

[69]Werner R A,Scheeres D J.Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia[J]. Celestial Mechanics and Dynamical Astronomy,1997,65 (3):313-344.

[70]Esposito P,Roth D,Demcak S.Mars Observer orbit determination analysis[J].Journal of Spacecraft and Rockets,1991,28(5):530-535.

[71]Hartmann W K.The shape of Kleopatra[J].Science,2000, 288(5467):820-821.

[72]Descamps P,Ostro S J,Hudson R S,et al.Radar observations of asteroid 216 Kleopatra[J].Science,2000, 288(5467):836-839.

[73]Marchis F,Berthier J.Triplicity and physical characteristics of Asteroid(216)Kleopatra[J].Icarus,2011,211(2):1022-1033.

[74]Descamps P,Marchis F,Berthier J,et al.Triplicity and physical characteristics of Asteroid(216)Kleopatra[J]. Icarus,2011,211(2):1022-1033.

[75]Ostro S J,Hudson R S,Nolan M C.Radar observations of asteroid 216 Kleopatra[J].Science,2000,288(5467): 836-839.

[76]Ostro S J,Rosema K D,Hudson R S,et al.Extreme elongation of asteroid 1620 Geographos from radar images [J].Nature,1995,375(6531):474-477.

[77]Hudson R S,Ostro S J.Physical model of asteroid 1620 Geographos from radar and optical data[J].Icarus,1999, 140(2):369-378.

[78]Chiorny V G,Hamanowa H,Reddy V,et al.Detection of the YORP effect in asteroid(1620)Geographos[J]. Astronomy&Astrophys,2008(489):25-28.

[79]Pravec P,Wolf M,ŠarounováL.Lightcurves of 26 near-Earth asteroids[J].Icarus,1998,136(1):124-153.

[80]Ryabova G O.Asteroid 1620 Geographos:I.Rotation[J]. Solar System Research,2002,36(2):168-174.

[81]Benner L A M,Hudson R S,Ostro S J,et al.Radar observations of asteroid 2063 Bacchus[J].Icarus,1999, 139(2):309-327.

[82]Hudson R S,Ostro S J.Shape of asteroid 4769 Castalia (1998 PB)from inversion of radar images[J].Science, 1994,263(5149):940-943.

[83]Hudson R S,Ostro S J,Harris A W.Constraints on spin state and hapke parameters of asteroid 4769 Castalia using lightcurves and a radar-derived shape model[J].Icarus, 1997,130(1):165-176.

[84]Mottola S,Erikson A,Harris A W,et al.Physical model of near-Earth asteroid 6489 Golevka(1991 JX)from optical and infrared observations[J].The Astronomical Journal,1997, 114(3):1234-1245.

[85]Müller T G,Sekiguchi T,Kaasalainen M,et al.Thermal infrared observations of the Hayabusa spacecraft target asteroid 25143 Itokawa[J].Astronomy and Astrophysics, 2005,443(1):347-355.

[86]Abe S,Mukai T,Hirata N,et al.Mass and local topography measurements of Itokawa by Hayabusa[J].Science,2006, 312(5778):1344-1347.

[87]Demura H,Kobayashi S,Nemoto E,et al.Pole and global shape of 25143 Itokawa[J].Science,2006,312(5778): 1347-1349.

[88]Fujiwara A,Kawaguchi J,Yeomans D K,et al.The rubblepile asteroid Itokawa as observed by Hayabusa[J].Science, 2006,312(5778):1330-1334.

[89]Hiroi T,Abe M,Kitazato K,et al.Developing space weathering on the asteroid 25143 Itokawa[J].Nature,2006, 443(7107):56-58.

[90]Saito J,Miyamoto H,Nakamura R,et al.Detailed Images of Asteroid 25143 Itokawa from Hayabusa[J].Science, 2006,312(5778):1341-1344.

[91]Taylor P A,Margot J L,VokrouhlickýD,et al.Spin rate of asteroid(54509)2000 PH5 increasing due to the YORP effect[J].Science,2007,316(5822):274-277.

[92]Veverka J,Farquhar B,Robinson M,et al.The landing of the NEAR-Shoemaker spacecraft on asteroid 433 Eros[J]. Nature,2001,413(6854):390-393.

[93]Connors M,Wiegert P,Veillet C.Earth's Trojan asteroid [J].Nature,2011,475(7357):481-483.

[94]Stooke P.Small body shape models.EAR-A-5-DDRSTOOKE-SHAPE-MODELS-V1.0.NASA planetary data system[R].Washington D.C.:NASA,2002.

[95]Neese C Ed.Small body radar shape models V2.0.EAR-A-5-DDR-RADARSHAPE-MODELS-V2.0,NASA Planetary Data System[R].Washington D.C.:NASA,2004.

[96]Riaguas A,Elipe A,Lara M.Periodic orbits around a massive straight segment[J].Celestial Mechanics and Dynamical Astronomy,1999,73(1/4):169-178.

[97]Riaguas A,Elipe A,López-Moratalla T.Non-linear stability of the equilibria in the gravity field of a finite straight segment[J].Celestial Mechanics and Dynamical Astronomy, 2001,81(3):235-248.

[98]Arribas A,Elipe A.Non-integrability of the motion of a particle around a massive straight segment[J].Physics Letters A,2001(281):142-148.

[99]Elipe A,Lara M.A simple model for the chaotic motion around(433)Eros[J].Journal of Astronomy Science,2003, 51(4):391-404.

[100]Romero S G,Palacián J F,Yanguas P.The invariant manifolds of a finite straight segment[J].Monografías de la Real Academia de Ciencias de Zaragoza,2004 (25):137-148.

[101]Blesa F.Periodic orbits around simple shaped bodies[J]. Monogr.Semin.Mat.García Galdeano,2006(33):67-74. [102]Fukushima T.Precise computation of acceleration due to uniform ring or disk[J].Celestial Mechanics and Dynamical Astronomy,2010,108(4):339-356.

[103]Linder J F,Lynn J,King F W,et al.Order and chaos in the rotation and revolution of a line segment and a point[J]. Physical Review E,2010(81):036208.

[104]Liu X,Baoyin H,Ma X.Equilibria,periodic orbits around equilibria,and heteroclinic connections in the gravity field of a rotating homogeneous cube[J].Astrophysics and Space Science,2011(333):409-418.

[105]Liu X,Baoyin H,Ma X.Periodic orbits in the gravity field of a fixed homogeneous cube[J].Astrophysics and Space Science,2011(334):357-364.

[106]Najid N E,Zegoumou M,Elourabi E H.Dynamical behavior in the vicinity of a circular anisotropic ring[J]. Open Astronomy Journal,2012(5):54-60.

[107]Liu X,Baoyin H,Ma X.Dynamics of surface motion on a rotating massive homogeneous body[J].Science China-Physics,Mechanics and Astronomy,2013(56):818-829.

[108]Li X,Qiao D,Cui P.The equilibria and periodic orbits around a dumbbell-shaped body[J].Astrophysics and Space Science,2013(348):417-426.

[109]Takahashi Y,Scheeres D J,Werner R A.Surface gravity fields for asteroids and comets[J].Journal of Guidance, Control,and Dynamics,2013,36(2):362-374.

[110]Asphaug E,Ostro S J,Hudson R S,et al.Disruption of kilometre-sized asteroids by energetic collisions[J].Nature, 1998,393(6684):437-440.

[111]Mirtich B.Fast and accurate computation of polyhedral mass properties[J].Journal of Graphics Tools,1996,1(2): 31-50.

[112]Scheeres D J,Ostro S J,Hudson R S,et al.Orbits close to asteroid 4769 Castalia,Icarus,1996(121):67-87.

[113]Scheeres D J,Ostro S J,Hudson R S,et al.Dynamics of orbits close to asteroid 4179 Toutatis.Icarus,1998, 132(1):53-79.

[114]Scheeres D J,Williams B G,Miller J K.Evaluation of the dynamic environment of an asteroid:applications to 433 Eros[J].Journal of Guidance,Control,and Dynamics, 2000,23(3):466-475.

[115]Scheeres D J.The orbital dynamics environment of 433 Eros [J].Ann Arbor,2002(1001):48109-2140.

[116]Scheeres D J,Broschart S,Ostro S J,et al.The dynamical environment about Asteroid 25143 Itokawa[C]∥Proceedings of the Twenty-Fourth International Symposium on Space Technology and Science.[S.l.]:[s.n.],2004: 456-461.

[117]Scheeres D J,Broschart S,Ostro S J,et al.The dynamical environment about Asteroid 25143 Itokawa:target of the Hayabusa Mission[C]∥Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit.[S.l.]: AIAA/AAS,2004:1-12.

[118]Scheeres D J.Orbital mechanics about small bodies[J]. Acta Astronautica,2012(7):21-14.

[119]Mondelo J M,Broschart S B,Villac B F.Dynamical analysis of 1:1 resonances near asteroids:application to Vesta[C]∥Proceedings of the 2010 AIAA/AAS Astrodynamics Specialists Conference.Toronto:[s.n.], 2010:1-15.

[120]Yu Y,Baoyin H.Orbital dynamics in the vicinity of asteroid 216 Kleopatra[J].The Astronomical Journal, 2012,143(3):62-70.

[121]Yu Y,Baoyin H.Generating families of 3D periodic orbits about asteroids[J].Monthly Notices of the Royal Astronomical Society,2012,427(1):872-881.

[122]Yu Y,Baoyin H.Resonant orbits in the vicinity of asteroid 216 Kleopatra[J].Astrophysics and Space Science,2013, 343(1):75 82.

[123]Jiang Y,Baoyin H,Li J,et al.Orbits and manifolds near the equilibrium points around a rotating asteroid[J]. Astrophysics and Space Science,2014(349):83-106.

[124]Jiang Y,Baoyin H.Orbital mechanics near a rotating asteroid[J].Journal of Astrophysics and Astronomy,2014, 35(1):17-38.

[125]Hirabayashi M,Scheeres D J.Analysis of Asteroid(216) Kleopatra using dynamical and structural constraints[J]. The Astrophysical Journal,2014,780(2):160-171.

[126]Chanut T G G,Winter O C,Tsuchida M.3D stability orbits close to 433 Eros using an effective polyhedral model method[J].Monthly Notices of the Royal Astronomical Society,2014(2383):1-11.

[127]Wang X,Jiang Y,Gong S.Analysis of the potential field and equilibrium points of irregular-shaped minor celestial bodies[J].Astrophysics and Space Science,2014(353): 105-121.

[128]Werner R A,Scheeres D J.Mutual potential of homogeneous polyhedra[J].Celestial Mechanics and Dynamical Astronomy,2005,91(3 4):337 349.

[129]Fahnestock E G,Scheeres D J.Simulation of the full two rigid body problem using polyhedral mutual potential and potential derivatives approach[J].Celestial Mechanics and Dynamical Astronomy,2006,96(3-4):317-339.

[130]Fahnestock E G,Scheeres D J.Simulation and analysis of the dynamics of binary near-Earth Asteroid(66391) 1999 KW4[J].Icarus,2008,194(2):410-435.

[131]Riaguas A,Elipe A,Lara M.Periodic orbits around a massive straight segment[J].Celestial Mechanics and Dynamical Astronomy,1999,73(1/4):169-178.

[132]Riaguas A,Elipe A,López-Moratalla T.Non-linear stability of the equilibria in the gravity field of a finite straight segment[J].Celestial Mechanics and Dynamical Astronomy,2001,81(3):235-248.

[133]Hu W,Scheeres D J.Spacecraft motion about slowly rotating asteroids[J].Journal of Guidance,Control,and Dynamics,2002,25(4):765-775.

[134]Hu W,Scheeres D J.Numerical determination of stability regions for orbital motion in uniformly rotating second degree and order gravity fields[J].Planetary and Space Science,2004,52(8):685-692.

[135]Provisional designations[EB/OL].[2014-07-30].http:// www.minorplanetcenter.net/iau/lists/Desigs.html.

[136]Igumenshchev I V,Shustov B M,Tutukov A V.Dynamics of supershells-Blow-out[J].Astronomy and Astrophysics, 1990(234):396-402.

[137]Iben Jr I,Tutukov A V.Helium star cataclysmics[J].The Astrophysical Journal,1991(370):615-629.

[138]Yungelson L R,Tutukov A V,Livio M.The formation of binary and single nuclei of planetary nebulae[J].TheAstrophysical Journal,1993(418):794-803.

[139]Firmani C,Tutukov A V.Bursting and stationary star formation in disks and nuclei of galaxies[J].Astronomy and Astrophysics,1994(288):713-730.

[140]Tutukov A V,Yungelson L R.Merging of binary white dwarfs neutron stars and black-holes under the influence of gravitational wave radiation[J].Monthly Notices of the Royal Astronomical Society,1994(268):871-879.

[141]Tutukov A V,Krügel E.The main types of star formation in galactic nuclei[J].Astronomy and Astrophysics, 1995(299):25-33.

[142]Tutukov A V,Yungelson L.Double-degenerate semidetached binaries with helium secondaries:cataclysmic variables,supersoft X-ray sources,supernovae and accretion-induced collapses[J].Monthly Notices of the Royal Astronomical Society,1996,280(4):1035-1045.

[143]Firmani C,Avila-Reese V,Ghisellini G,et al.Formation rate,evolving luminosity function,jet structure,and progenitors for long gamma-ray bursts[J].The Astrophysical Journal,2004,611(2):1033-1045.

[144]Acharova I A,Lépine J R D,Mishurov Y N,et al.A mechanism for the formation of oxygen and iron bimodal radial distribution in the disc of our Galaxy[J].Monthly Notices of the Royal Astronomical Society,2010,402(2): 1149-1155.

[145]Tutukov A V,Fedorova A V.Formation of planets during the evolution of single and binary stars[J].Astronomy reports,2012,56(4):305-314.

[146]Moore,C.Braids in classical dynamics[J].Physical Review Letters,1993,70(24):3675-3679.

[147]Galán J,Munoz-Almaraz F J,Freire E,et al.Stability and bifurcations of the figure-8 solution of the three-body problem[J].Physical Review Letters,2002,88 (24):241101.

[148]Šuvakov M,DmitrašinoviV.Three classes of newtonian three-body planar periodic orbits[J].Physical Review Letters,2013,110(11):114301.

[149]Jon Cartwright.Physicists discover a whopping 13 new solutions to three-body problem.science.now[EB/OL]. (2013-03-08).http://news.sciencemag.org/physics/2013/ 03/physicists-discover-whopping-13-new-solutions-threebody-problem.

[150]Hiroi T,Abe M,Kitazato K,et al.Developing space weathering on the asteroid 25143 Itokawa[J].Nature, 2006,443(7107):56-58.

[151]Kleine T,Münker C,Mezger K,et al.Rapid accretion and early core formation on asteroids and the terrestrial planets from Hf-W chronometry[J].Nature,2002,418(6901): 952-955.

[152]Sánchez P,Scheeres D J.Simulating asteroid rubble piles with a self-gravitating soft-sphere distinct element method model[J].The Astrophysical Journal,2011,727(2):120.

[153]Tancredi G,Maciel A,Heredia L,et al.Granular physics in low-gravity environments using discrete element method [J].Monthly Notices of the Royal Astronomical Society, 2012,420(4):3368-3380.

[154]Tobias S M,Dagon K,Marston J B.Astrophysical fluid dynamics via direct statistical simulation[J].The Astrophysical Journal,2011,727(2):127-138.

[155]Genel S,Vogelsberger M,Nelson D,et al.Following the flow:tracer particles in astrophysical fluid simulations[J]. Monthly Notices of the Royal Astronomical Society,2013, 435(2):1426-1442.

[156]Smale S.Mathematical problems for the next century[J]. The Mathematical Intelligencer,1998,20(2):7-15.

[责任编辑:宋宏]

Research Trend of Dynamics in the Gravitational Field of Irregular Celestial Body

JIANG Yu1,2BAOYIN Hexi2
(1.State Key Laboratory of Astronautic Dynamics,Xi'an Satellite Control Center,Xi'an 710043,China; 2.School of Aerospace Engineering,Tsinghua University,Beijing 100084,China)

Both asteroid and comet exploration are important areas in the deep space exploration.The mass of an asteroid or a comet is not big enough,so its gravitational force is much smaller than the stress to satisfy the hydrostatic equilibrium,which makes the minor celestial body irregular-shaped.The research of dynamical behaviours and mechanisms in the gravitational field of irregular celestial body is the basis of minor celestial body exploration,including the catching of the explorer and the design of the orbit around the minor celestial body.This paper summarizes the research progress of the dynamics in the gravitational field of irregular celestial body through gravitational models and dynamical mechanisms.The research situation of gravitational models such as the Legendre polynomial model,the simple-shaped model and the polyhedron model are presented.In addition,the research situation of dynamical mechanisms such as the periodic orbits and quasi-periodic orbits,equilibrium points, manifolds,bifurcations and resonances,chaos,are also presented.Besides,we have analyzed key points and difficult points of these researches.Finally,the research trend of the dynamics in the gravitational field of irregular celestial body is discussed.

irregular celestial body;asteroid exploration;comet exploration;astronautic dynamics;dynamical law

V448.2

:A

:2095-7777(2014)04-0250-12

10.15982/j.issn.2095-7777.2014.04.002

姜宇(1983—),男,博士研究生,工程师,主要研究方向为不规则天体引力场中的拓扑动力系统等。

E-mail:jiangyu_xian_china@163.com

宝音贺西(1972—),男,博士,博士生导师,教授,主要研究方向为航天器轨道理论等。

E-mail:baoyin@tsinghua.edu.cn

2014-07-30

2014-08-30

国家重点基础研究发展计划(973)计划资助项目(2012CB720000);国家自然科学基金资助项目(11372150);宇航动力学国家重点实验室基金资助项目(2014ADL-DW02)