基于SINS/CNS组合导航系统的多模型自适应估计算法

范双菲,赵方方,李夏菁,唐忠樑,贺威

(1.弗吉尼亚理工大学计算机工程系,弗吉尼亚24060;2.电子科技大学机器人研究中心,成都611731)

基于SINS/CNS组合导航系统的多模型自适应估计算法

范双菲1,赵方方2,李夏菁2,唐忠樑2,贺威2

(1.弗吉尼亚理工大学计算机工程系,弗吉尼亚24060;2.电子科技大学机器人研究中心,成都611731)

针对单一模型滤波器在未知或不确定的系统参数下适应性较差的问题,提出了一种新的基于多模型自适应估计(multiple model adaptive estimation,MMAE)的滤波方法。该方法利用改进的卡尔曼滤波代替传统的卡尔曼滤波,比如扩展卡尔曼滤波(extended Kalman filter,EKF)和无迹卡尔曼滤波(unscented Kalman filter, UKF)。EKF和UKF被用来作为多模型自适应估计的子滤波器,从而实现对非线性系统的状态估计。同时,还将该方法应用于基于弹道导弹模型的组合导航中实现了系统仿真。仿真结果表明,与传统的EKF和UKF算法比较,改进的滤波方法可以解决传统模型滤波器适应性差的问题,并提高系统的导航精度。

多模型自适应估计;卡尔曼滤波;捷联惯导;天文导航;组合导航

0 引 言

随着信息技术的发展,导航的精度在导航领域内的要求越来越高。然而仅仅通过一种导航技术来获取高精度的弹道导弹的运动状态是很难的。捷联惯性导航系统(strap-down inertial navigation system,SINS)是一种自主式的导航系统,相对精度比较高,计算代价较低,但误差随时间积累,所以它在较长时间内不能独立地工作。天文导航系统(celestial navigation system,CNS)利用天空中的恒星作为导航信号源,具有隐蔽性好、自主性强、定向、定位精度高,且不随工作时间的增长而降低精度的优点,但是它易受气候条件的限制,通常不能单独完成导航定位的[1-2]。功能在误差特性上二者存在互补性,通过相互组合可以达到提高导航性能的目的[3]。在国外,组合导航系统取得了较为显著的应用效果。组合导航系统的优点很多,例如能有效地利用各子系统的信息,相互取长补短,使得系统定位精度大大提高;进一步提高了子系统的可靠性;扩大了对气候、环境、海域等的适应能力等[4]。因此, SINS/CNS组合导航系统被广泛地应用到弹道导弹模型中。

滤波算法在组合导航系统中起到了非常重要的作用,滤波算法通常会被用于估计非测量状态量和滤波噪声测量值。在信息融合中,卡尔曼滤波是一种最典型的滤波算法,来获得目标的位置、速度和姿态信息[5]。在卡尔曼滤波的框架下,多种滤波方法发展起来,比如扩展卡尔曼滤波和无迹卡尔曼滤波。

由于弹道导弹运动模型的非线性,传统的卡尔曼滤波方法很难估计导航信息。然而对于非线性系统,扩展卡尔曼滤波和无迹卡尔曼滤波是更为可行的滤波方法。EKF的基本思想是将非线性系统方程在当前状态估计值处展开成泰勒级数,然后按线性方程进行处理。但在非线性较高的情况下,线性化会导致滤波器具有较低的性能和散度。因此,对于非线性较严重的系统,EKF可能会导致更大的测量误差,而UKF是一种更为合适的滤波方法。该方法的优点是无须计算雅各比矩阵,无须对状态方程和测量方程线性化,因此也就没有对高阶项的截断误差,就可以获得更高的精度。与EKF相比, UKF最大的特点是采用无迹变换(unscented transformation,UT),UT通过传播均值和协方差来获得概率密度函数。因此,UKF可以有效地解决系统的非线性问题[6-7]。

通常,我们假设扩展卡尔曼滤波和无迹卡尔曼滤波的处理噪声和测量噪声均为零均值高斯白噪声。这样就导致了经典的滤波器调谐的问题[8]。在实际中一个滤波器的调谐是费力且耗时的。一种常用的解决方法就是使用自适应滤波器。自适应滤波器可以被分为以下四种基本类型:贝叶斯估计(Bayesian)、最大似然估计(maximum likelihood)、协方差匹配(covariance matching)和相关系数法(correlation approach)。其中,贝叶斯和最大似然方法更适用于多模型法。

多模型自适应估计是多模型自适应控制中的一个重要方面,对于解决具有变结构和参数不确定性的系统问题非常有效。多模型自适应估计最早是由Magill在1965年提出的,它通过带有不同参数值的滤波器估计的加权值得到对系统状态的估计,从而达到对于未知的或不确定性的系统参数自适应的目的[9]。

本文的主要贡献是提出了适用于非线性系统的多模型自适应估计滤波算法。同时,把改进后的多模型自适应滤波算法在弹道导弹模型下进行仿真。对扩展卡尔曼滤波、无迹卡尔曼滤波、多模型自适应扩展卡尔曼滤波和多模型自适应无迹卡尔曼滤波四种滤波算法的仿真结果进行了对比。

1 多模型自适应估计滤波算法

1.1 多模型自适应估计

多模型自适应估计是由一个并行的卡尔曼滤波器库和假设检验算法组成的。在滤波器库中,每一个滤波器都具有特定的系统模型,其内在的卡尔曼滤波器模型由独立的矢量参数来描述。每个卡尔曼滤波器根据自身的模型和输入的矢量,形成对当前的系统状态的估计。然后,利用得到的估计值形成对量测量的预测值,再将该预测值与实际的量测量相减得到残差。假设检验算法将各个滤波器形成的残差来指示各个滤波器的模型与系统实际的模型相近程度。残差越小,说明滤波器的模型与系统实际模型越匹配。在量测值和实际矢量参数的条件下,假设检验算法利用该残差值来计算各卡尔曼滤波器模型的条件概率。得到的条件概率被用来衡量各个卡尔曼滤波器的状态估计值的正确性。对各个状态估计值取概率加权平均值,从而形成对实际系统的混合状态估计[10-11]。多模型自适应估计具体处理流程如图1所示。

多模型自适应估计是一个使用一组基于一些未知参数的滤波器的递归估计器。未知参数为处理噪声协方差,用向量P表示,其中假设其为常数。我们不需要先给出状态值和输出处理值的固定估计值,即使时变状态和输出的矩阵是可被利用的。一组有一些已知P的概率分布函数产生的分布值,表示为p(P),其中｛P(l);l=1,2,…,M｝。估计过程的目的就是确定P(l)中第l个元素的条件概率,从而给出当前时刻的估计值。贝叶斯法则应用如下所示:

图1 多模型自适应估计处理流程图Fig.1 Multiple model adaptive estimation process flow chart

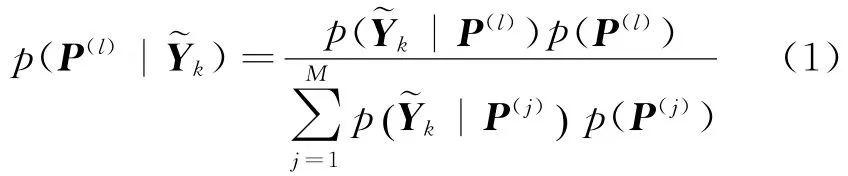
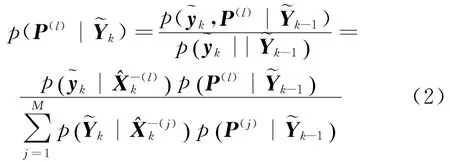
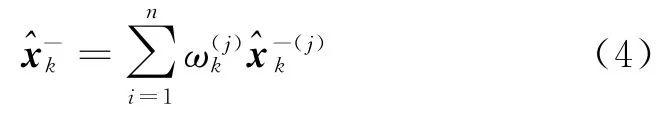
同时,状态估计的误差协方差即可通过下式计算得到

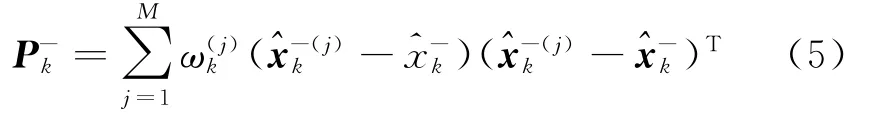
在tk时刻对P的特定估计表示为,其协方差矩阵表示为Pk,它们的表达式分别为

1.2 似然方程

然后,建立测量余量的似然方程。首先,余量的定义为

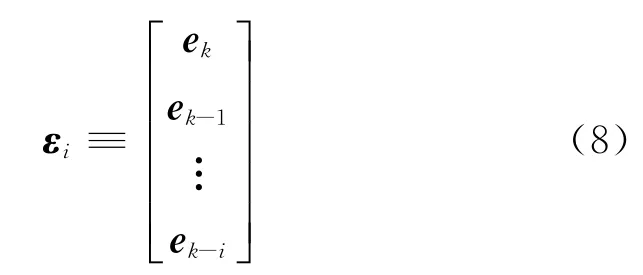
与εi相关的似然方程为

当i=0时,似然方程即可简化为

1.3 自适应法则

在标准多模型自适应估计算法中,只有当前时刻的测量信息用于更新法则中。因此更新法则如下:

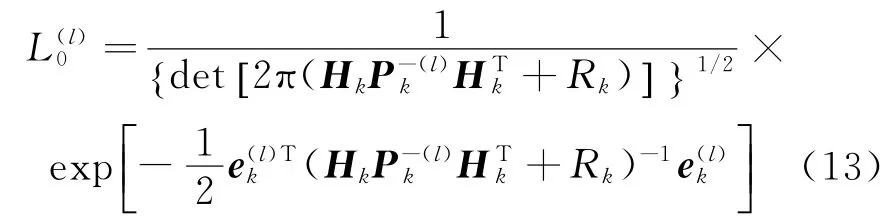
2 多模型自适应估计算法的应用

2.1 弹道导弹运动模型

弹道导弹的运动可以分为三个阶段,助推段的垂直上升部分、助推段的转弯部分还有最后的熄火部分[12]。我们假设地球是一个固定的球体,导弹是一个质点,就能够得到如下的非线性系统

式中:p为推力;Xd为空气阻力;θ为发射点重力坐标系下的俯仰角;θ0为发射时的俯仰角;θk为第二阶段末尾的俯仰角;g为重力加速度。

为了避免地球转动所导致的坐标变化,需要在发射点处将重力坐标系转变为惯性坐标系。通过一级速度积分,可以得到在发射点处惯性坐标系的位置。在发射点处,导弹的绝对加速度是惯性坐标系中速度的导数。加速度计的误差被建模为一级马尔科夫的过程。基于式(16)、式(17)中的绝对加速度与视加速度αib,最终可通过将α转变到导弹坐标系中并将一级马尔科夫过程加入,从而得到加速度计的输出。同时,也能通过在导弹坐标系的姿态角速率中加入高斯噪声,来得到陀螺仪在相同时刻的输出。

加速度计的输出为

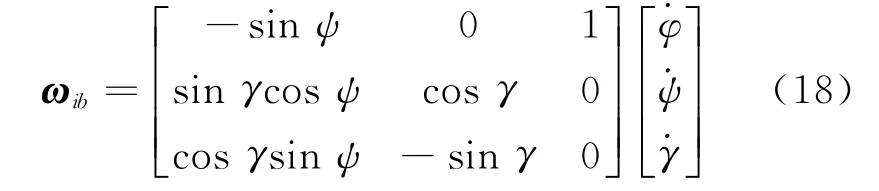
式中:φ,ψ,γ分别为俯仰角、航向角和横滚角。

天文导航系统通常利用星敏感器来寻找星空,然后提取出恒星的图像位置来识别图像,并最终从姿态矩阵中得到姿态信息[13]。在天文导航系统中,星敏感器的输出是惯性坐标系统中姿态角的观测值。且M为弹体坐标系与惯性坐标系之间的姿态转换矩阵

如果假定系统具有附加噪声,那么为了产生离散时间动态系统中的状态空间,公式则变为如下的表达形式

式中:xk为系统状态矢量;yk为观测状态矢量;ωk和vk分别为处理噪声矩阵和测量噪声矩阵。

2.2 SINS/CNS组合导航系统

高可靠、高精度的定位信息对于众多系统来说都是必需的。组合导航系统能有效地利用各子系统的信息,相互取长补短,使得系统定位精度大大提高;进一步提高子系统的可靠性;提高了导航自动化程度。因此,采用捷联惯性导航与天文导航组合,组成以惯性导航为主体的导航系统,用天文导航系统的信息来修正惯性导航系统中的位置、速度和姿态等导航信息[14]。在组合导航系统中,利用星光信息做观测量,采用多模型自适应滤波技术,得到物理平台的漂移角、陀螺仪和加速度计的误差以及其它的导航参数的误差。

天文导航系统利用星敏感器测量星光信息来确定载体的姿态。SINS/CNS系统的组合安装方式是捷联方案,即将星敏感器与机体固连[15]。采用捷联方案的优点是结构简单、成本低、使用灵活,缺点是星敏感器工作在动态的环境中,需较大的视场角。根据导弹飞行比较平稳的特点,采用捷联方案,以降低成本[16]。导航系统的工作流程如图2所示,其中Δ^X为惯性导航系统误差的估计值。

组合导航系统比简单的惯导系统的精度高是因为在惯性空间里恒星的方位基本上保持不变的。尽管星敏感器的像差、地球极轴的进动和章动以及视差等因素使恒星方向有微小的变化,但是他们所造成的姿态误差小于1°。因此这个星敏感器就相当于没有漂移的陀螺,所以可以用天文量测信息惯性器件误差。

在捷联惯性与天文导航组合的方式中,星敏感器进行搜索星空、捕获星体、然后进行星图识别,提取恒星的成像位置,通过图像识别后,从星敏感器姿态矩阵中计算得到姿态大小[17]。姿态角可表示为

式中:(ψ,φ,γ)分别为航向角、俯仰角和横滚角;(x, y)为恒星在星敏感器中成像的位置;(α,β)分别为恒星的赤经、赤纬;f为星敏感器的焦距。而惯性导航系统通过惯性导航解算会给出载体的三轴姿态信息(航向角ψ、俯仰角φ和横滚角γ),因此将两者相减就可以得到载体的三轴姿态误差角。

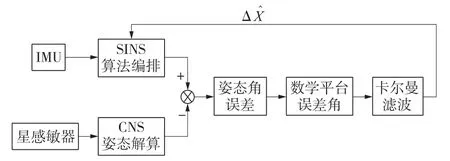
图2 SINS/CNS组合导航系统工作流程Fig.2 SINS/CNS integrated navigation workflow chart

3 仿真校验

在这章中,将给出基于弹道导弹模型的SINS/ CNS组合导航的多模型自适应估计算法的仿真过程与验证结果。

3.1 仿真条件

为了验证所改进的多模型自适应估计算法的滤波效果,进行了系统仿真。通常假设一组处理噪声协方差随时间变化的参数值,但是在实际情况下,不可能在设计子滤波器时事先已知系统的时变处理噪声协方差参数。因此考虑到参数的未知性,在设计各子滤波器的模型集时,通过比较多种产生均匀观察随机分布的函数,选用伪随机序列对每个子滤波器的模型参数进行配置。然后通过仿真观察其对系统状态的滤波效果,并与其它滤波算法的滤波效果进行了比较。

在仿真过程中,滤波算法分别用到了扩展卡尔曼滤波、无迹卡尔曼滤波、基于扩展卡尔曼滤波的多模型自适应估计、基于无迹卡尔曼滤波的多模型自适应估计。仿真的初始参数如表1所示。

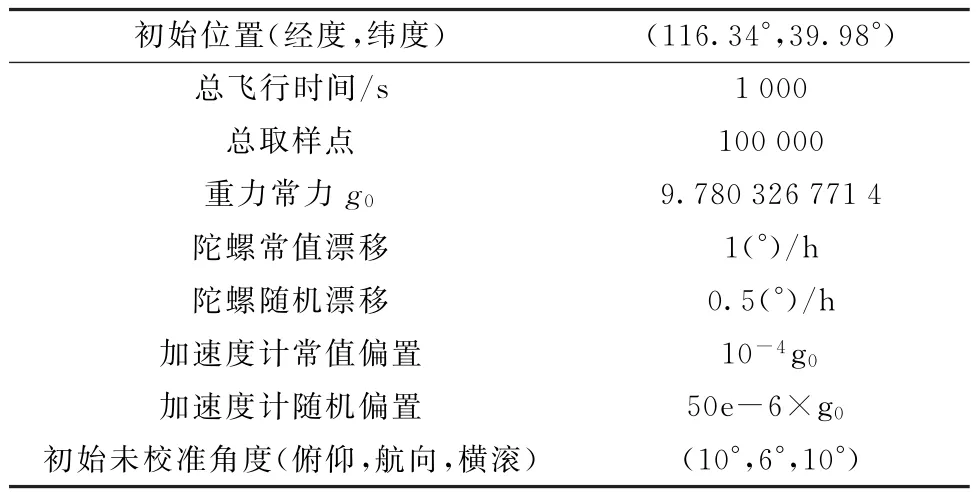
表1 初始参数Table 1 Initial Parameters

其中需注意的是在扩展卡尔曼滤波和无迹卡尔曼滤波的仿真中,处理噪声协方差矩阵中的wgt和wga参数所用的值均为wgt0和wga0,即分别为2.424 1e-06和4.890 2e-04。9×9的处理噪声协方差矩阵参数化为wgt和wga,如式(23)所示:

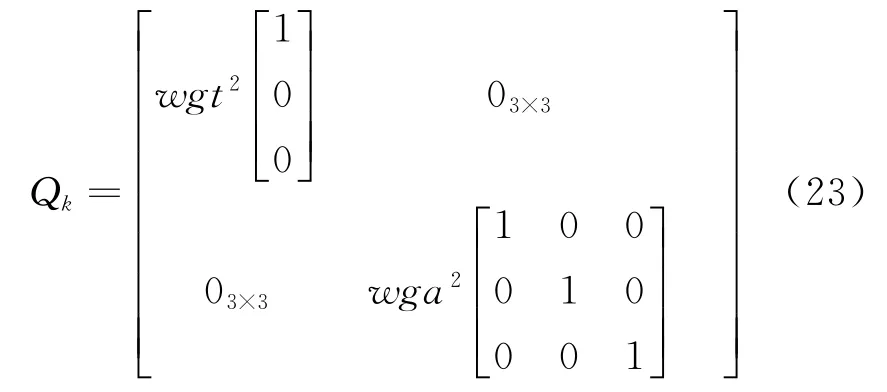
由于在实际的时变系统中,处理噪声协方差参数未知,且其分布有很多可能值,因此需要选择一种好的方法来产生一个随机分布。在这里选Hammersley[18]伪随机序列,分别对两种产生随机数的方法得到的效果进行了比较。其中第一种方法伪随机数产生方法中的线性同余法,第二种方法则为拟随机数产生方法中的Hammersley点集。在仿真过程中,在[0,1]中随机产生了250个点,如图3所示。

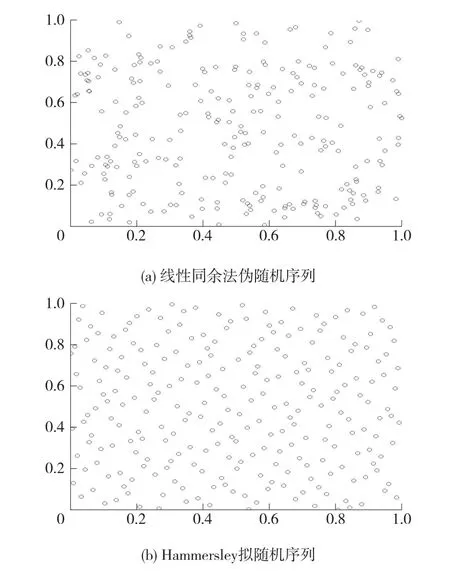
图3 均匀分布和Hammersley拟随机序列对比图Fig.3 Uniform distribution and Hammersley quasi-random sequence comparison

从图3中可以清楚地看到,与均匀分布相比, Hammersley伪随机序列能够提供更均匀的分布。

为了突显该算法在实际的时变系统中滤波效果的优势,为每一个子滤波器设置参数和时,就采用Hammersley点集来为每个子滤波器分布参数。在仿真过程中,多模型自适应扩展卡尔曼滤波和多模型自适应无迹卡尔曼滤波中分别选用10个子滤波器,且其和参数的值由Hammersley点集产生。

对于系统的参数设置,此时假设了一组处理噪声协方差随时间变化的参数数据,即弹道导弹的总飞行时间为1 000 s。前500 s,处理噪声协方差的两个参数和分别为0.5倍的和0.5倍的;后500 s,处理噪声协方差的两个参数和分别为2倍的和2倍的。

3.2 仿真结果

上述四种滤波方法的仿真结果如图4、图5、图6所示。

图4 航向角误差Fig.4 The error of course angle

根据上面的仿真结果图不难看出,不论是在非自适应滤波方法还是自适应滤波方法中,无迹卡尔曼滤波的误差较扩展卡尔曼滤波更小,即滤波效果更好;与自适应滤波方法相比,不论子滤波器用的扩展卡尔曼滤波还是无迹卡尔曼滤波,由于是单一参数值,无法适应时变系统,因此不难看出多模型自适应估计的滤波效果明显优于非自适应估计。

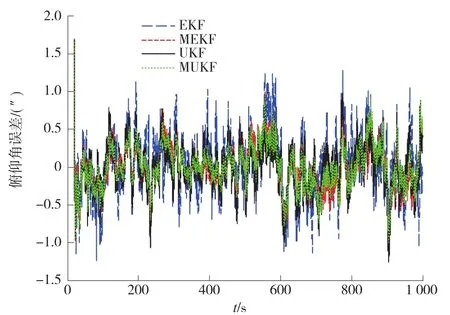
图5 俯仰角误差Fig.5 The error of pitch angle

图6 横滚角误差Fig.6 The error of roll angle

为了更清楚地看出这几种方法的优劣性,在表2中给出了这四种滤波算法估计姿态误差的均方根。因此,在上述四种方法中,能够得到最优估计的即为子滤波器应用无迹卡尔曼滤波的多模型自适应估计方法,如表2所示。

表2 不同滤波算法的滤波效果Table 2 The filtering effect of different filtering algorithms

4 结 论

本文提出了新的多模型自适应滤波方法,并将改进后的滤波算法在弹道导弹运动模型下应用于SINS/CNS组合导航系统中。为了清楚指出改进后滤波算法的导航性能,我们实现了仿真并对四种滤波方法做了比较。通过对航向角、横滚角和俯仰角的误差分析可以得出,多模型自适应扩展卡尔曼滤波和多模型自适应无迹卡尔曼滤波有更好的滤波效果。此外,当系统是时变的或系统参数是未知的情况下,改进的多模型自适应算法是最适合的算法。总的来说,改进的滤波方法能满足弹道导弹的需求,多模型自适应无迹卡尔曼滤波获得最好的滤波效果,整体上可提高组合导航系统的导航精度。

进一步的研究可将如今研究较热的扩展粒子滤波和无迹粒子滤波放入子滤波器中进行仿真,并比较滤波效果。

[1]Xiong Z,Liu J Y,Yu F,et al.Research of airborne INS/ CNS integrated filtering algorithm based on celestial angle observation[J].Journal of Astronautics,2010,31(2): 397-402.

[2]Wang J J,Yu J Q,Wang L.Analysis of application of a new integrated navigation system of the tactical missiles[C]∥Chinese Control Conference(CCC).[S.l.]:CCC,2014: 653-657.

[3]吴伟仁,王大轶,宁晓琳.深空探测器自主导航原理与技术[M].北京:中国宇航出版社,2011:57-62.[Wu W R,Wang D Y,Ning X L.The principle and technology of deep space autonomous navigation[M].Beijing:China Astronautic Publishing House,2011:57-62.]

[4]王小旭,赵琳.自适应融合滤波算法及其在INS/GPS组合导航中的应用[J].宇航学报,2010,31(11):2504-2511.[Wang X X,Zhao L.Adaptive fusion filtering algorithm and its application for INS/GPS integrated navigation system[J]. Journal of Astronautics,2010,31(11):2504-2511.]

[5]陈培,杨颖,王云,等.扩展卡尔曼滤波估计载波参数的算法研究[J].电子科技大学学报,2009,38(4):509-512.[Chen P,Yang Y,Wang Y,et al.Estimation for carrier parameters based on the extended Kalman filter[J].Journal of University of Electronic Science and Technology of China, 2009,38(4):509-512.]

[6]吴楠,陈磊.高速声速滑翔再入飞行器弹道估计的自适应卡尔曼滤波[J].航空学报,2013,34(8):1960-1971.[Wu N, Chen L.Adaptive Kalman filtering for trajectory estimation of hypersonic glide reentry vehicles[J].Acta Aeronautica et Astronautica Sinica,2013,34(8):1960-1971.]

[7]胡正东,郭才发,张士峰,等.Unscented卡尔曼滤波在飞航导弹地磁导航中的应用[J].宇航学报,2009,30(4):1443-1448.[Hu Z D,Guo C F,Zhang S F,et al.Application of unscented Kalman filter in geomagnetic navigation for aerodynamic missile[J].Journal of Astronautics,2009, 30(4):1443-1448.]

[8]Kong F C,Dai G L,Cai L.The composed correcting Kalman filtering method for integrated SINS/GPS navigation system [C]∥Intelligent Computing and Intelligent Systems(ICIS), 2010 IEEE International Conference on.[S.l.]:IEEE, 2010,2:408-412.

[9]李艳华,房建成.一种多模型自适应联邦滤波器及其在INS/ CNS/GPS组合导航系统中的应用[J].航天控制,2003, 21(2):33-38.[Li Y H,Fang J C.A multi-model adaptive federated filter and its application in INS/CNS/GPS integrated navigation system[J].Aerospace Control,2003, 21(2):33-38.]

[10]陈金广,李洁,高新波.双重迭代变分贝叶斯自适应卡尔曼滤波算法[J].电子科技大学学报,2012,41(3):360-363. [Chen J G,Li J,Gao X B.Dual recursive variational bayesian adaptive kalman filtering algorithm[J].Journal of University of Electronic Science and Technology of China, 2012,41(3):360-363.]

[11]熊凯,魏春玲.基于多模型自适应估计的航天器相对导航[J].系统科学与数学,2014,34(7):828-837.[Xiong K,Wei C L.Spacecraft relative navigation based on multiple model adaptive estimator[J].Journal of Systems Science and Mathematical Sciences,2014,34(7):828-837.]

[12]Shima T,Oshman Y,Shinar J.Efficient multiple model adaptive estimation in ballistic missile interception scenarios [J].Journal of Guidance,Control,and Dynamics,2002, 25(4):667-675.

[13]Qu C S,Xu H L,Ying T.SINS/CNS integrated navigation solution using adaptive unscented Kalman filtering[J]. International Journal of Computer Applications in Technology,2011,41(1):109-116.

[14]Ning X L,Fang J C.Spacecraft autonomous navigation using unscented particle filter-based celestial/Doppler information fusion[J].Measurement Science and Technology,2008, 19(9):095203.

[15]宁晓琳,房建成.一种基于纯天文观测的火星车自主导航方法[J].空间科学学报,2006,26(2):142-147.[Ning X L, Fang J C.A new autonomous navigation method for martian rover based on celestial observation[J].Chinese Journal of Space Science,2006,26(2):142-147.]

[16]Nebelecky C K,Crassidis J L,Singla P.A model error formulation of the multiple model adaptive estimation algorithm[C]∥Information Fusion,2014 17th International Conference.[S.l.]:[s.n.],2014:1-8.

[17]邓红,刘光斌,陈昊明,等.发射惯性坐标系下误差角与数学平台失准角的推导与仿真[J].宇航学报,2011,32(4): 781-786.[Deng H,Liu G B,Chen H M,et al.Deduction and simulation of angular error relationship in“SINS/CNS”integrated navigation system[J].Journal of Astronautics, 2011,32(4):781-786.]

[18]Hammersley J M.Monte Carlo methods for solving multivariable problems[J].Proceedings of the New York Academy of Sciences,1960,86(3):844-874.

通信地址:电子科技大学机器人研究中心

电话:(028)61830633

E-mail:weihe@ieee.org

[责任编辑:高莎]

Multiple Model Adaptive Estimation Algorithm for SINS/CNS Integrated Navigation System

FAN Shuangfei1,ZHAO Fangfang2,LI Xiajing2,TANG Zhongliang2,HE Wei2
(1.Computer Engineering Department,Virginia Polytechnic Institute and State University,Blacksburg VA 24060,USA; 2.Center for Robotics,University of Electronic Science and Technology of China,Chengdu 611731,China)

In this paper,a new filtering method based on multiple model adaptive estimation(MMAE)algorithm is proposed,for the problem of poor adaptability of single model filters with unknown or uncertain parameters.In this proposed algorithm,we use improved Kalman filters rather than traditional Kalman filters,such as extended Kalman filter(EKF),unscented Kalman filter(UKF).And EKF and UKF are used as sub filters in MMAE algorithm to realize the state estimation of nonlinear system.Meanwhile,this method is applied to the SINS/CNS integrated navigation system under the motion of ballistic missile.As the simulation result shows,the improved filtering methods have better navigation accuracy,and can solve the problem of poor adaptability of single model filter,when compared with traditional EKF and UKF algorithms.

multiple model adaptive estimation;Kalman filter;strap-down inertial navigation;celestial navigation;integrated navigation

V448

:A

:2095-7777(2014)04-0275-07

10.15982/j.issn.2095-7777.2014.04.005

贺威(1984—),男,教授,博士,主要研究方向:智能控制系统、机器人技术、人机交互系统。

2014-07-10

2014-07-30

国家重点基础研究发展计划(2014CB744206)