基于月面单幅图像的软着陆障碍识别与安全区选取方法

吴伟仁,王大轶,毛晓艳,黄翔宇

(1.探月与航天工程中心,北京100037;2.北京控制工程研究所,北京100190; 3.空间智能控制技术重点实验室,北京100094)

基于月面单幅图像的软着陆障碍识别与安全区选取方法

吴伟仁1,王大轶2,3,毛晓艳2,3,黄翔宇2,3

(1.探月与航天工程中心,北京100037;2.北京控制工程研究所,北京100190; 3.空间智能控制技术重点实验室,北京100094)

针对月球软着陆自主避障的需求,提出了一种适合月球灰尘表面的改进优化Hapke模型,给出了相对高程的求解、障碍识别与安全区选取方法,解决了已有纹理法无法识别坡度的问题,实现了利用单幅图像的月面着陆障碍识别与安全区域选取。利用月球软着陆下降段仿真图像,进行了模型解算和三维高程恢复并计算安全区域,结果表明,利用月面单幅图像能够实现障碍的识别与安全区的选取。

障碍识别;灰度重构形状;朗伯体模型;Hapke模型

0 引 言

月球是一个无大气天体,在其自身地质活动、各种流星天体撞击以及炙热太阳照射的影响下,月球表面分布着高山、壑谷、陡坡以及各种各样的岩石和陨石坑等。这种地形、地貌以及石块和陨石坑等使探测器安全着陆存在较大风险。早期的月球着陆探测任务,限于当时技术水平,Lunar系列和勘察者系列月球探测器都不具备识别障碍和避障能力,导致着陆成功率非常低。Apollo系列则是通过宇航员观测着陆区并操纵人控系统实现了避障和安全着陆[1]。可见,只有着陆器具有发现和识别障碍并进行机动避障的能力,才能保证软着陆的高安全和高可靠。

目前地外天体着陆器配备的障碍识别敏感器主要包括光学敏感器和激光三维扫描仪。其中激光三维扫描仪体积功耗大且成像时间较长,扫描时刻需要着陆器位置稳定进行悬停[2]。而光学敏感器体积功耗小,瞬时成像,对着陆器无严格的位置速度要求,被列为首选方案。目前,国内外利用光学敏感器所成图像进行软着陆障碍识别的方法多为立体视觉法和纹理分析法[3]。其中立体视觉法对图像特征分布要求较高,为了达到一定的精度需要较长的基线。纹理分析法根据阴影分布判断障碍,不能对缓坡等亮度缓变的危险区域进行有效识别。针对这些问题,Horn等人提出一种利用单幅图像的地貌重构方法(shape from shading,SFS),其原理是利用物体成像表面亮度的变化,参照表面反射特性或形状的附加约束,解析出物体表面矢量信息,转化得到表面深度信息,从而完成形状的重构。该方法仅利用单幅影像的灰度信息,便可重构像素点的相对高程,测量信息更完备,对图像本身的特征要求较少,相比已有方法具有明显的优势。但实际的月球表面反射特性并不符合SFS算法采用的理想朗伯体反射模型,而且月球表面还有灰尘覆盖,因此,已有的SFS算法无法实现月球表面着陆下降图像的形状恢复。针对此问题,本文提出了一种适合月球灰尘表面的改进优化Hapke模型,并给出了相对高程的求解、障碍识别与安全区选取方法,实现了利用单幅图像的月面着陆障碍识别。

1 灰度重构形状方法

SFS方法成立的前提有三个:1)光源为无限远处点光源;2)反射模型为朗伯体表面反射模型;3)成像关系为正交投影。

SFS算法基本思路描述如下。

如图1所示,朗伯体表面反射模型[4]为

式中:E为图像亮度;Li为入射光强;ρ为表面反射率,均为常量;θi为入射角。消除Li和ρ的影响,归一化可得E=cosθi。

图1 朗伯体反射模型Fig.1 Lambert reflection model

基于上述的三点假设,物体表面的亮度方程可以表示为:

光源矢量a=(-ps,-qs,1),表面矢量N=(-p,-q,1),则,得到经归一化处理,消除I0的影响,简化为

SFS原型问题可描述为

其中:E(x,y)为归一化后的图像灰度值;Ω是所感兴趣的地形表面所处的区域,目标就是求取使得上式达到极小的p和q。

在构造能量函数时,目前主要采用的约束条件有以下几种。

光滑性约束:

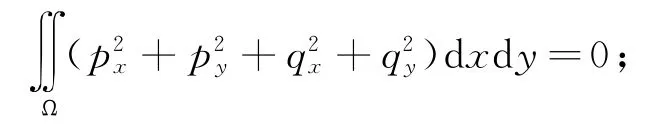
可积性约束:

亮度梯度约束:

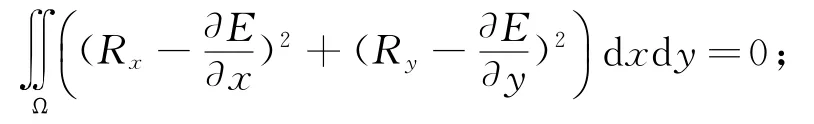
单位法矢量约束:

式中:px表示对x的偏导数,,py、qx、qy、zx、 zy、Rx及Ry等定义同上。

2 解算方法

目前,世界上的SFS解算方法大致可分为最小值方法[5]、演化方法[6]、局部方法[7]和线性化方法[8]等四大类。这几类算法具有各自不同的特点,下面对这几种算法的唯一性、收敛性、稳定性,以及对真解的逼近程度和适用范围等方面进行简要说明。

最小值方法是将物体表面反射模型和光滑表面模型均表示为能量函数的形式,然后再将它们联合表示为一个泛函极值问题或最优化控制问题,使相应问题取最小值的解即为SFS问题的解。最小值方法充分考虑了在图像成像过程中各种可能的约束,这些附加约束和原亮度方程联立求解时,能够产生较为稳定和精确的解。但是算法在搜索最小值时,由于初始条件未知,容易陷入局部极小值。且该方法一般使用泛函变分和松弛迭代法求解,收敛速度过慢。

演化方法主要是求解Hamilton-Jacobi方程,从已知的初始条件或边界条件出发,随着时间参数的变化确定出所有图像点对应的物体表面点形状及高度。解算过程利用了相关可微的一些性质,隐式地表示并应用了物体的光滑表面模型,通常可以找到全局最优值。由于该方法是把光滑性假设融入算法中而不是作为单独的约束函数,可以避免由于引入二阶微分而导致的过光滑问题。但这种方法的计算复杂性过高,计算量随图像增大而增加,而且对先验知识的要求比较严格,不适用于复杂物体和实际含噪图像。

局部方法是将反射模型和物体表面局部形状假设相结合构成关于物体局部形状参数的线性偏微分方程组,利用边界条件可求得该方程的唯一解。常用的局部形状假设为球形表面假设。这种方法简单直观,对于具有光滑表面的合成图像恢复效果较好,但是当被恢复物体表面不具有局部球面特征时,算法失效。

线性化方法则认为在非线性反射函数中,低阶项占主要部分,通过对反射函数线性化,从而将SFS基本模型转化为一个线性问题求解。Pentland方法采用傅立叶变换,Tsai的方法使用了表面梯度的离散近似,但是这两种方法各有针对性,都是对某一种图像适用,某些情况下误差较大或算法失效。

综上所述,局部方法和线性化方法同属于在局部进行计算的方法,都是基于特定的假设,能通过稳定收敛的算法得到一个近似解。算法相对比较简单,不需要正则化过程,同时也因为不需要关于遮挡边界或者奇异点的先验信息,抗噪性较好,并且对解的搜索限制在线性空间中,算法速度比最小值方法和演化方法两种全局化方法提高了许多。其中,线性化方法计算过程相对简单快捷,对目标的属性要求不高,选择作为后续求解的首选方法。

3 改进的Hapke模型

漫反射光照模型是一种理想的模型,并不适用于所有的天体表面,针对月球环境需要修改反射模型。本文引入了Bruce Hapke教授提出的Hapke模型[9],该模型可以用来描述月球等天体表面的辐射强度。它主要是针对由单个光源引起的天体反射情况,根据光线在天体表面反射的几何特性,以及天体表面对光线的反射系数,计算出由天体表面反射的光线到达观察位置的辐射强度。图2显示了Hapke模型中光源、目标与视点的几何关系。

图2 光源与视点的几何关系Fig.2 Geometry relation between sun source and inspect point

此时模型表示为

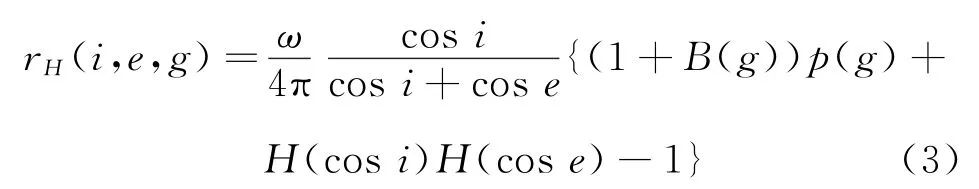
式中:i为入射角,表示入射光线与表面法线之间的夹角;e为反射角,表示出射方向与表面法线之间的夹角;g为相角,表示入射光线和出射方向之间的夹角;ω为单次散射反照率,0＜ω＜1;B(g)表示视点方向与光源方向重合的条件,,其中h是粗糙度参数,与介质表面的空隙度、颗粒大小分布有关。

p(g)表示单位角散射方程,用于描述光线被陆地土壤散射时的角度分布情况

其中:cos g=cos i cos e+sin i sin e cosφ,b和c是描述月壤的参数。

cos i和cos e可以分别由天体表面梯度矢量和入射、出射矢量的乘积来表示,即

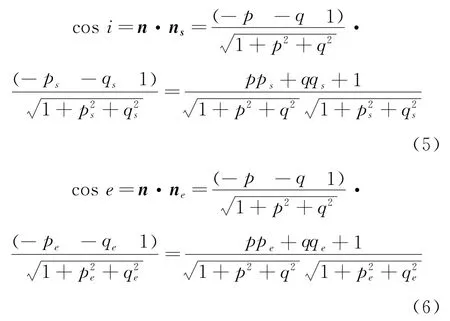
尽管Hapke模型被认为是目前最稳定的计算天体表面反射系数的模型,但是其仍然存在着一个突出的问题,即当光线的反射角与入射角接近的时候,光源的方向矢量与视点的方向矢量非常接近,此时Hapke模型会出现奇异性,计算的结果会出现较大的误差。为此,需要对其进行改进。

改进方法如下:假设B(g)为0且p(g)为1,其中p(g)为1表示散射方程具有等方向性,此时相位角可忽略不计。这样既简化了Hapke模型的表达式,又保证其不会出现奇异性,且保留了Hapke模型的基本性质。改进模型可表示为

改进模型的解法采用线性化方法,利用有限差分思想将F离散化

根据图像差分的基本思想,以上各项得如下表示

假设初始高度为Z0,Z*为真解,对图像中(i,j)点进行Taylor展开得

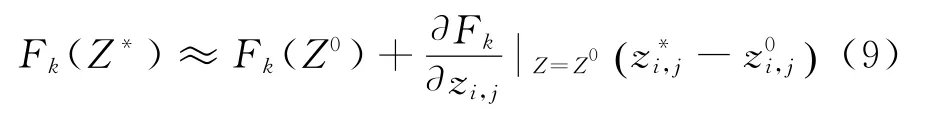
则最后的迭代公式可写为

4 地形识别结果

对着陆月球的下降段图像进行仿真如图3所示。

利用Hapke模型的计算结果如图4所示。

可以看出,Hapke模型可以有效地恢复地形图的相对三维信息,地形起伏与实际地形相符,较为准确。

图3 月球着陆下降段仿真图像Fig.3 Simulative image during landing on lunar

图4 Hapke模型的计算结果Fig.4 Calculation result based on Hapke model

5 障碍识别与着陆区选取方法

前面给出的SFS方法得到的是视场内场景的相对高程值,可以在一次成像中给出月面足够密集点的相对高度信息,但其高度值并非实际的高度,而是归一化的数值表示。因此,采用类似三维高程图获取坡度和粗糙度的计算方法对每个像点进行比较分析,找出视场范围内相对最平坦的、满足降落尺寸要求的区域。

1)确定平均坡面法线。采用最小二乘法拟合出一定单元区域(包含Ni,j个数据点)的平均坡面法线,具体表达式为

式中:h为Ni,j维的全1列向量,即h= [1 1…1］T;G为利用单元区域的数据点构造的Ni,j×3矩阵,具体表达式为

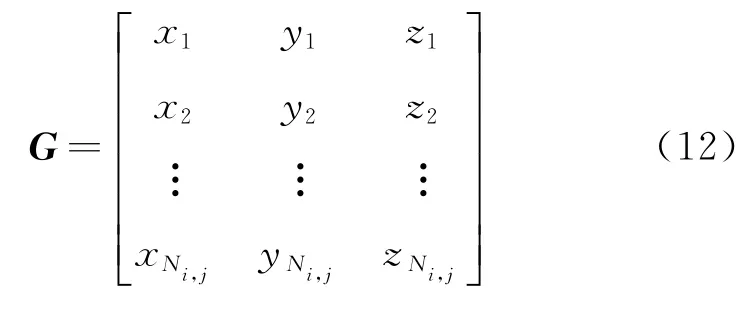
2)计算平均坡度。根据平均坡面法线计算该单元区域的平均坡度为

式中:b=[0 0 1］T,表示垂直向量。

3)计算障碍高度。根据平均坡面估算该单元区域内每个单元格的障碍高度

在上述判断的基础上,根据坡度和高度进行分类,得到障碍二值图,障碍像素点置1,安全像素点置0。

4)确定安全着陆点。如图5所示,将图像划分为网格,在障碍二值图的基础上,以图像中心开始螺旋前进搜索,直至找到符合安全着陆要求的着陆区域为止,确定安全着陆点。若在视场范围内难以找到完全满足要求的安全着陆区域,则根据坡度和安全半径的加权判断选取最优的区域作为安全着陆区,确定安全着陆点。根据图3选取的安全着陆点如图6所示。

图5 安全半径螺旋搜索算法Fig.5 Helix searching algorithm for safe radius

图6 选取的安全着陆点Fig.6 Selection for safe landing point

6 结 论

针对月球软着陆过程的障碍识别问题,本文引入了灰度重构形状方法,并提出了一种适合月球灰尘表面的改进优化Hapke模型,实现了利用单幅月表图像的地貌重构与安全区选取。利用月球软着陆下降段仿真图像,进行了三维高程恢复和安全区域选取方法的仿真验证,仿真结果表明:

1)采用改进Hapke模型的灰度重构形状方法,利用单幅图像能够实现高程信息的重构,结果可信。利用相对高程信息可以进行坡度的估算,弥补了单幅图像不能准确识别坡度的缺陷;

2)根据得到的高程信息实现的障碍识别和安全着陆点选取,能够选取到实际的安全着陆点,可用于月球自主软着陆。

[1]Klumpp A R.Apollo guidance,navigation and control[R]. [S.l.]:NASA,1971.

[2]张洪华,梁俊,黄翔宇,等.嫦娥三号自主避障软着陆控制技术[J].中国科学:技术科学,2014,44(6):559-568.[Zhang H H,Liang J,Huang X Y,et al.Autonomous hazard avoidance control for Chang'E-3 soft landing[J].Chinese Science,2014,44(6):559-568.]

[3]Andres Huertas,Yang C.Passive imaging based multicue hazard detection for spacecraft safe landing[R].[S.l.]:ISAIRAS,2006.

[4]Horn B K P.Obtaining shape from shading information.the psychology of computer vision[M].[S.l.]:McGraw Hill, 1975:115-155.

[5]Horn B K P.Height and gradient from shading[J]. International Journal of Computer Vision,1990,5(1): 37-75.

[6]Kimmel R,Bruckstein A M.Tracking level sets by level sets:a method for solving the shape from shading problem [J].CVIU.,1995,62(2):47-58.

[7]Dupuis P,Oliensis J.Direct method for reconstructing shape from shading[C]∥IEEE Computer Society Conference on CVPR.Urbana Champaign:IEEE,1992:453-458.

[8]Pentland A.Shape information from shading:a theory about human perception[C]∥Prov.Intl.Conf.CV.Tampa:[s. n.],1998:404-413.

[9]Hapke B.Bidirectional reflectance spectroscopy.the coherent backscatter opposition effect and anisotropic scattering[J]. Icarus,2002(157):523-534.

通信地址:北京市西城区车公庄大街12号10层(100037)

电话:(010)88306176

E-mail:wuwr2002@vip.sina.com

[责任编辑:高莎]

Obstacle Recognition and Safe Area Selection Method in Soft Landing based on a Single Lunar Image

WU Weiren1,WANG Dayi2,3,MAO Xiaoyan2,3,HUANG Xiangyu2,3
(1.Lunar Exploration and Space Program Center,Beijing 100037,China; 2.Beijing Institute of Control Engineering,Beijing 100190,China; 3.Science and Technology on Space Intelligent Control Laboratory,Beijing 100094,China)

A method of ameliorated Hapke model which is the same with satellite surface covered with deep dust is put forward to satisfy the needs of soft landing on the moon.The linearization method is used to calculate the differential equation and to get the relative three-dimensional height of simulative images for obstacle recognition and selection of safe area during landing phase.It can resolve the problem that is difficult to recognize the slope by texture method.Making use of the simulating lunar images during landing,the model calculation,three-dimensional height rebuilding and safe area selection are realized.The results show the validity of this method using single lunar image.

obstacle recognition;shape from shading;Lambert model;Hapke model

V19

:A

:2095-7777(2014)04-0262-07

10.15982/j.issn.2095-7777.2014.04.003

吴伟仁(1953—),男,研究员,博士生导师,国防科工局探月与航天工程中心,中国探月工程总设计师。主要研究方向为测控通信与航天系统工程技术。

2014-10-30

2014-11-30

国家中长期科技发展规划重大专项资助项目;民用航天预先研究项目