隔震支座主要参数对基础隔震结构双向地震响应的影响

潘 毅，季晨龙，韩徐扬，卢立恒

（1.西南交通大学a.土木工程学院；b.陆地交通地质灾害防治技术国家工程实验室，成都610031；2.安徽省城建设计研究院，合肥230001）

基础隔震是在结构物底部设置隔震消能装置，来达到延长结构自振周期、耗散地震能量，从而达到降低结构地震响应的目的。隔震支座参数可以在一个较大范围内变化，不同的支座参数将会直接影响结构的隔震效果。因此，隔震支座参数对结构地震响应的影响受到了不少学者的关注。Jain等［1］认为地震动本身的特性和支座主要参数对结构的地震响应会造成一定的影响，并以1栋6层钢筋混凝土框架结构为例对其进行了探讨。赵伟等［2］通过改变摩擦摆支座滑道的摩擦系数对单层球面网壳的地震响应展进行了分析，得到了摩擦系数对结构地震响应的影响规律。王建强等［3］研究了摩擦摆支座滑道半径和摩擦系数对框剪结构地震响应的影响，发现二者对结构自振周期、楼层加速度和位移均存在显著影响。孙君等［4］研究了铅芯隔震支座参数的变化对网架结构水平隔震效果的影响，并给出了网架结构水平隔震设计的建议。花磊等［5］分析了隔震支座力学特性、上部结构力学特性和地震动特性对隔震结构地震响应的影响，得到了这三个因素对基础隔震结构地震响应的影响方式。杜永峰［6］等针对工程界比较关注的柱串联隔震系统的水平刚度问题，建立了水平刚度计算公式，探讨了压应力对水平刚度及结构地震响应的影响，得到了水平刚度随着压应力的增大而减少的结论。Mishra［7］等考察了隔震支座参数的不确定性对结构地震响应的影响，并发现这种影响是较为显著且不可忽略的。

上述学者在隔震支座参数对基础隔震结构地震响应影响的研究中已取得了许多成果，但亦存在一定的不足。目前，基础隔震分析时大多采用单向地震动输入，而在双向甚至多维地震动作用下影响的研究相对较少。笔者针对基础隔震结构在双向地震动作用下的隔震结构响应做了一定研究，得到了双向地震动作用下隔震结构地震响应的规律以及频谱特性对隔震结构地震响应的影响［8－9］。在已有研究的基础上，本文主要研究在双向地震动作用下，隔震支座的3个主要参数（等效水平刚度Kf、屈服前刚度K1和屈服力Qd）对结构地震响应的影响，分析了在4种典型地震动作用下隔震结构的地震响应，得到其对隔震结构地震响应的影响规律，以期为隔震结构设计提供有益的借鉴。

1 隔震结构计算模型

未设置隔震支座时，任意时刻结构的动力方程为

设置隔震支座后，式（1）变为

隔震层有一定的质量，但相对于上部结构总体质量，是可以忽略的。因此，此时式（2）的总体刚度矩阵［K］和总体阻尼矩阵［C］是隔震支座的刚度矩阵［K］r和阻尼矩阵［C］r与原刚度矩阵［K］0和原阻尼矩阵［C］0的叠合。式中｛F｝为恢复力列向量。

2 SAP2000的叠层橡胶支座的恢复力模型

由于是研究双向地震动对隔震结构地震响应的影响，因此，在SAP2000中选择可以考虑双向耦合作用的Rubber Isolator单元［10］。该单元对两个剪切变形有耦合的塑性属性，对每一个剪切变形自由度均可独立的指定线性或非线性行为。其对余下的4个变形有线性的有效属性。

当两个剪切自由度均为非线性时，耦合的力 变形关系为

式中：k2和k3为弹性弹簧系数；σy2和σy3为屈服力；r2和r3为屈服后刚度对屈服前刚度的比例。这些变量的范围为代表屈服；du2和du3为支座屈服位移；σy2、σy3为屈服力；z表示内部滞后变量，z2和z3的初始值为0，其变化符合式（5）。

其中

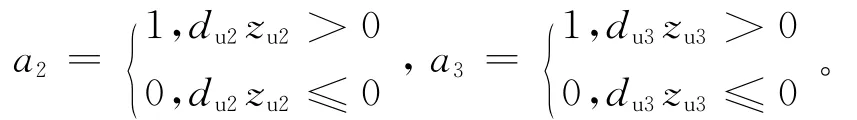
3 工程概况

以1栋7层钢筋混凝土框架结构为例，丙类建筑，混凝土强度等级为C25，层高为3.6m，柱网尺寸为5m×5m，柱截面尺寸为600mm×600mm，梁截面尺寸为400mm×500mm，如图1所示。其中，不上人屋面活载为0.5kN／m2，恒载大小为4kN／m2；楼面恒载和活载分别为4、2kN／m2；顶层梁线荷载为5kN／m，其它层梁线荷载大小为15kN／m。

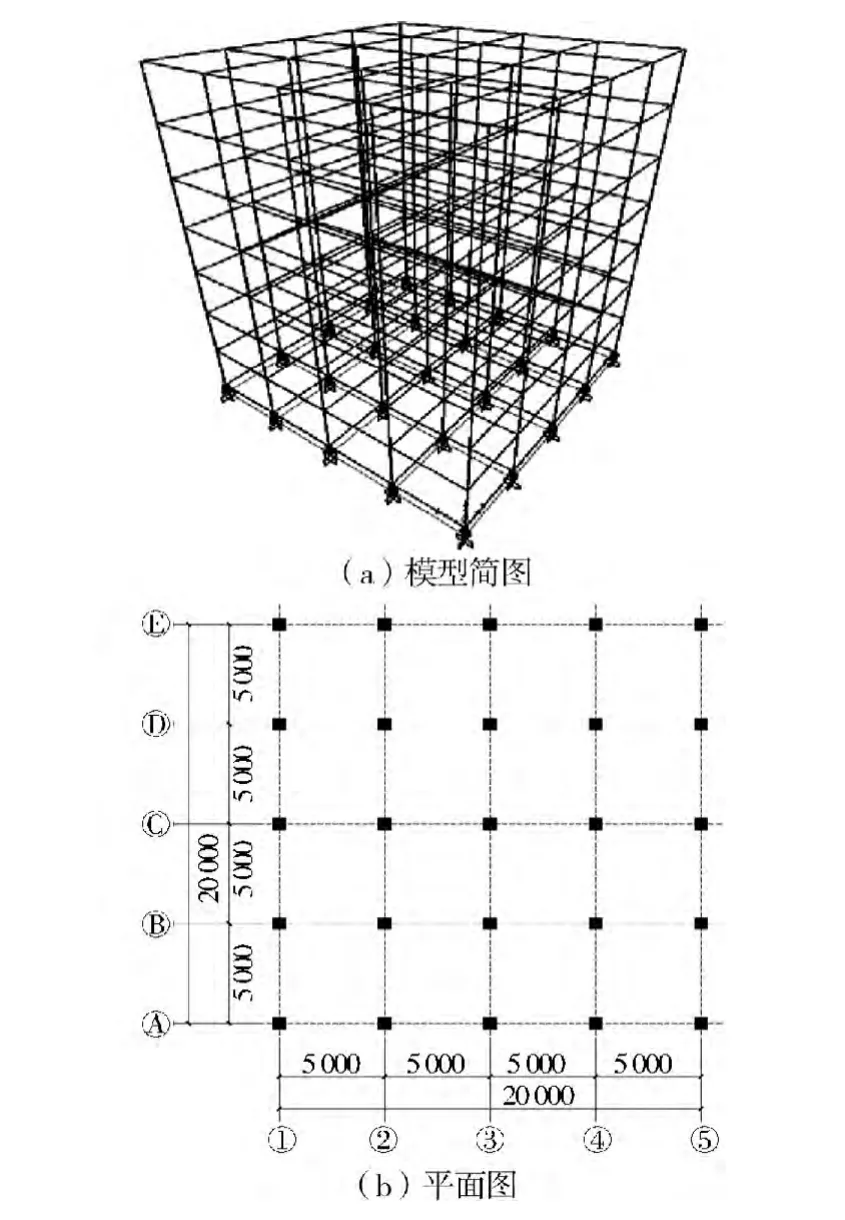
图1 结构模型简图

采用有限元软件SAP2000，对基础隔震结构进行水平双向地震动作用的时程分析。对结构从X、Y向同时输入地震波，并取X向与Y向加速度峰值之比为1：0.85。由于所选结构在两个方向上对称。因此，没有研究当X向与Y向加速度峰值比为0.85：1的工况。所选地震波为迁安波（对应Ⅰ类场地）、Taft波（对应Ⅱ类场地）、El－Centro（对应Ⅲ类场地）和上海波（对应Ⅳ类场地），各条地震波反应谱如图2所示。

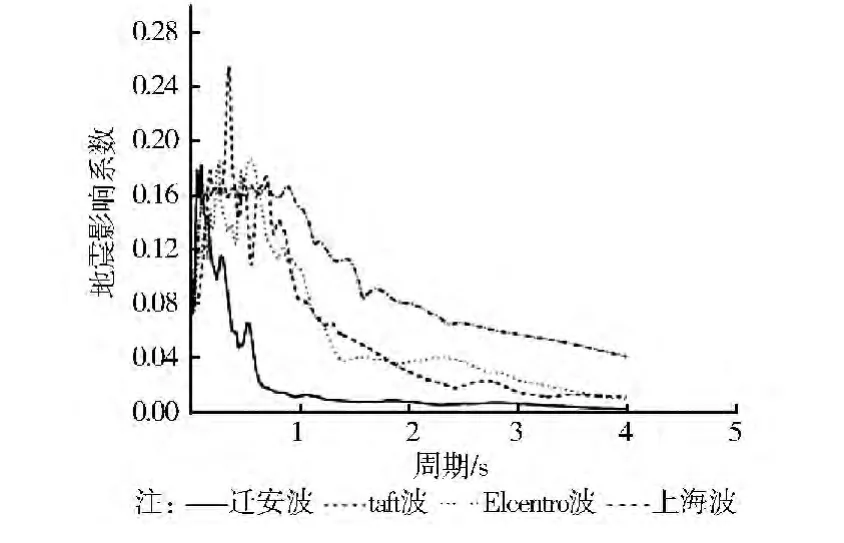
图2 地震波反应谱

4 支座参数对结构地震响应的影响

由于篇幅所限，仅讨论隔震支座的3个主要参数（等效水平刚度Kf、屈服前刚度K1、屈服力Qd）对结构顶层加速度最大值、隔震层位移最大值和基底剪力最大值的影响。根据中国《建筑结构抗震设计规范》［11］的相关要求，对输入的地震动加速度峰值进行调幅，使罕遇地震（8度0.2g）下加速度最大值为400gal。

4.1 等效水平刚度Kf

文献［12］给出了考虑等效水平刚度时，结构自振周期计算式为

由（6）式可以推导出等效水平刚度和结构自振周期的关系式为

式中：Tf为隔震结构的自振周期；M为隔震结构的质量；Kf为隔震结构的等效水平刚度。

结构刚度决定其自振周期，对于基础隔震结构而言，等效水平刚度Kf越大，自振周期Tf就越短，结构的响应方式就越类似于普通抗震结构。因此，随着等效水平刚度Kf的增大，结构顶层加速度最大值和基底剪力最大值应该逐渐增大，而隔震层位移最大值应逐渐减小。

为研究等效水平刚度Kf的变化对结构地震响应的影响，通过控制隔震支座的具体参数，分别建立自振周期为1.4、1.6、1.8、2.0、2.2、2.4s的6种模型。各个模型对应的隔震支座参数，如表1所示。

在前述4种地震动作用下，考察结构顶层加速度最大值、隔震层位移最大值和基底剪力最大值的变化情况，如图3～5所示。

表1 各模型对应的隔震支座参数

图3 等效水平刚度对结构顶层加速度最大值的影响

由图3和图5知，在Ⅰ、Ⅱ、Ⅲ类场地上，顶层加速度最大值和基底剪力最大值均随着等效水平刚度Kf的增大而增大；隔震层位移最大值则减小，如图4所示。而在Ⅳ类场地上，当结构自振周期大于1.8s时，基底剪力不仅没有降低反而增大。这是由于软弱场地滤掉了上海波的高频成分，延长结构的自振周期只能增加而不能降低结构的地震响应。此时，基底剪力数值整体也较大，最小值都达到了5 176kN，显著大于其它类场地的基底剪力。

从图4可看到，在所有4种类型的场地上，隔震层位移最大值均随等效水平刚度Kf的增大而逐渐减小。但在Ⅰ、Ⅱ类场地上，隔震层位移最大值对等效水平刚度Kf的变化不敏感，此时隔震层位移最大值均较小。而在Ⅲ、Ⅳ类场地上，当结构自振周期大于1.8s时，位移最大值的降幅较大，明显大于Ⅰ、Ⅱ类场地的降幅。

4.2 屈服前刚度K1

图4 等效水平刚度对隔震层位移最大值的影响

图5 等效水平刚度对基底剪力最大值的影响

为研究支座屈服前刚度K1对结构地震响应的影响，选定以下6种屈服前刚度（分别为4 000、5 000、7 000、9 000、10 000和12 000kN／m）进行分析。同时，为了避免其它参数对计算结果的影响，将其余参数设为定值，如表2所示。

表2 不同屈服前刚度的隔震支座参数

基础隔震结构在上述4种地震动作用下，顶层加速度最大值、隔震层位移最大值和基底剪力最大值随屈服前刚度K1变化的曲线，如图6～8所示。

图6 屈服前刚度对顶层加速度最大值的影响

图7 屈服前刚度对隔震层位移最大值的影响

由图6～8可知，X、Y向结构地震响应的变化趋势整体一致。

顶层加速度最大值随屈服前刚度K1的增大而逐渐增大。在所有4种类型的场地上，顶层加速度最大值的增幅均较大，即此时结构响应对屈服前刚度K1的增大较为敏感。其中，Ⅳ类场地上加速度最大值显著大于其他3类场地的相应值。

隔震层位移最大值随屈服前刚度K1的增大而逐渐减小。在Ⅰ、Ⅱ、Ⅲ类场地上，隔震层位移最大值对屈服前刚度K1的变化不敏感；在Ⅳ类场地上，位移最大值随K1的增大而显著降低，且在该类场地上，位移最大值显著大于其他3类场地的相应值。

图8 屈服前刚度对基底剪力最大的影响

在所有4种类型的场地上，基底剪力最大值均随屈服前刚度K1的增大而逐渐增大，但增幅较小。当结构位于Ⅳ类场地时，基底剪力最大值显著大于其它3类场地的相应值。

4.3 屈服力Qd

对采用6种不同屈服力Qd支座的结构模型进行考察，从而研究屈服力Qd对结构地震响应的影响。各个结构支座屈服力分别为50、60、70、90、100和120kN。隔震支座其他参数，如表3所示。在4种典型的地震动作用下，基础隔震结构顶层加速度最大值、隔震层位移最大值和基底剪力最大值如图9～11所示。

表3 不同屈服力隔震支座参数

由图9～11可知，顶层加速度最大值和基底剪力最大值均随屈服力Qd的增大而增大，而隔震层位移最大值则随屈服力Qd的增大而减小。

图9 屈服力对顶层加速度最大值的影响

图10 屈服力对隔震层位移最大值的影响

在所有4种类型的场地上，顶层加速度最大值对屈服力Qd的增大最敏感。在Ⅳ类场地上，结构顶层加速度最大值显著大于其它3类场地上的相应值。而当结构位于前3类场地时，隔震层位移最大值均小于Ⅳ类场地的相应值，且其降幅也不如Ⅳ类场地的降幅显著。基底剪力最大值随屈服力Qd增加而增大，且Ⅳ类场地上的基底剪力最大值也明显大于其它3类场地的相应值。

5 支座参数对水平向减震系数影响

为使设计人员更直观了解隔震支座参数对隔震效果的影响，分析3个支座参数对基础隔震结构水平向减震系数的影响，如图12～14所示。此时，输入地震动加速度最大值按8度0.2g设防烈度地震加速度最大值进行调整，调整后地震加速度最大值为196gal。

图11 屈服力对基底剪力最大值的影响

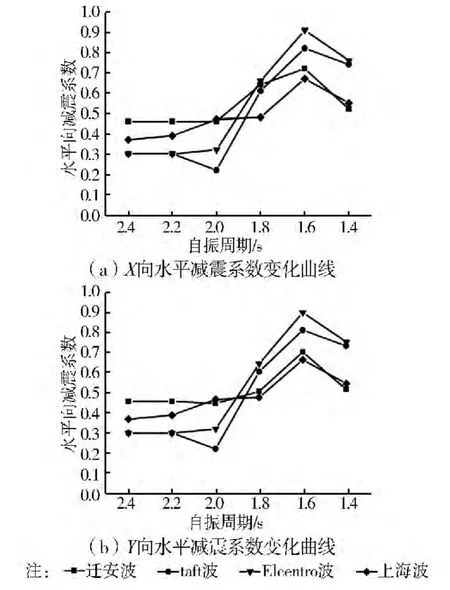
图12 等效水平刚度对水平向减震系数的影响

由图12可知，在双向地震动作用下，X与Y向的水平减震系数总体增大趋势一致，即随着等效水平刚度Kf的增大，水平向减震系数逐渐增大。可以看到，当结构自振周期等于1.6s时，水平向减震系数达到峰值，且该周期点附近减震数值也较大，即此时减震的效果最差，设计时应考虑予以避开该周期范围。特别应注意，当结构自振周期较长（大于或等于2.0s时），在Ⅳ类场地上，水平向减震系数始终大于前3类场地上的相应数值，即此时减震效果相对较差。

图13 屈服前刚度对水平向减震系数的影响

图14 屈服力对水平向减震系数的影响

屈服前刚度K1对基础隔震结构水平向减震系数的影响可以从图13看到。两个方向上减震系数曲线的增大趋势基本一致，即水平向减震系数总体上随屈服前刚度K1的增大而增大。当屈服前刚度K1小于7 000kN／m时，在所有4种类型的场地上，水平向减震系数均较小且互相差距不大。而当屈服前刚度K1大于7 000kN／m之后，Ⅰ、Ⅱ类场地的减震系数明显大于Ⅲ、Ⅳ类场地的减震系数，并且在屈服前刚度K1达到10 000kN／m时，减震系数达到最大值，即此时隔震效果相对最差。

从图14可以看到，两个方向上减震系数曲线随屈服力Qd增大的增幅总体一致。在Ⅱ、Ⅲ、Ⅳ类场地上，基础隔震结构水平向减震系数随着屈服力Qd增加而增加，即减震效果是在逐渐降低的。但当结构位于Ⅰ类场地时，减震系数先随屈服力Qd的增大而增加，当屈服力Qd大于80kN后，减震系数曲线显著降低，然后不随屈服力Qd的增大而变化，基本维持一定值。

6 结 论

1）隔震支座主要参数（Kf、K1、Qd）对不同场地类型的基础隔震结构在双向地震作用下的顶层加速度最大值和基底剪力最大值均有显著影响。而各参数（Kf、K1、Qd）对隔震层位移最大值的影响需根据场地类型具体考虑。

2）在Ⅰ、Ⅱ、Ⅲ类场地上，随着Kf、K1、Qd增大，基础隔震结构在双向地震作用下的加速度最大值和基底剪力最大值均呈明显的上升趋势，但隔震层位移最大值的变化相对较小。其中，Kf对顶层加速度最大值和基底剪力最大值的影响最大，二者的最大增幅分别达到了55.3%和72.1%，而屈服前刚度K1和屈服力Qd的影响相对小些，在K1和Qd的影响下，加速度最大值和基底剪力最大值的最大增幅分别为19.5%、8.5%和8.9%、11.6%；在Ⅳ类场地上，隔震支座主要参数（Kf、K1、Qd）对隔震层位移最大值的影响较大，且有相同的规律性，即随着Kf、K1、Qd增大，隔震层的位移最大值不断减小，最大减幅达80%以上。

3）基础隔震结构的减震效果与隔震支座主要参数和场地类型均有关。一般而言，随着支座屈服力Qd的降低，基础隔震结构的水平减震系数减小，即隔震效果更好。但在Ⅰ类场地上，降低隔震支座屈服力Qd可能反而造成水平减震系数增大的不利影响，在工程设计时应特别注意。

（致谢：本文的研究工作得到了西南交通大学高层次教师队伍建设专项资金资助。）

［1］Jain S K，Thakkar S K.Seismic response of six－storey base isolated building subjected to earthquakes of different characteristics［J］.Journal of the Institution of Engineers，1999，80（2）：64－69.

［2］赵伟，薛素铎，李雄彦，等.摩擦摆支座的摩擦系数对结构隔震性能影响分析［C］／／第16届全国结构工程学术会议论文集，2007：287－292.

［3］王建强，陈磊河，攸青言，等.支座滑道半径对摩擦摆基础隔震结构地震反应的影响［J］.地震工程与工程振动，2011，31（4）：132－136.Wang J J，Chen L H，You Q Y，et al.Influence of radius of spherical surface on the seismic responses of baseisolated structure with friction pendulum system ［J］.Earthquake Engineering and Engineering Vibration，2011，31（4）：132－136.

［4］孙君，李爱群，丁幼亮.铅芯橡胶支座参数变化对大跨空间网架水平隔震效果的影响［J］.防灾减灾工程学报，2008，28（2）：208－212.Sun J，Li A Q，Ding Y L.Influence of parameters of lead laminated rubber bearing on the horizontal seismic isolation for long－span space truss structures ［J］.Journal of Disaster Prevention and Mitigation Engineering，2008，28（2）：208－212.

［5］花磊，何文福，刘文光，等.隔震层参数及地震动特性对隔震结构地震响应的影响［J］.水电能源科学，2010，28（7）：85－88，97.Hua L，He W F，Liu W G，et al.Effects of isolator and ground motion characteristics on the performance of seismic－isolated buildings ［J］.Water Resources and Power，2010，28（7）：85－88，97.

［6］杜永峰，朱前坤，李慧.串联隔震系统水平刚度及对结构地震响应影响［J］.振动与冲击，2011，30（11）：21－24.Du Y F，Zhu Q K，Li H.Horizontal stiffness of laminated rubber bearing serially connected with column and its effects on seismic response of isolated structure［J］.Journal of Vibration and Shock，2011，30（11）：21－24.

［7］Mishra S K，Chakraborty S.Performance of a baseisolated building with system parameter uncertainty subjected to a stochastic earthquake ［J］.International Journal of Acoustics and Vibrations，2013，18（1）：7－19.

［8］潘毅，季晨龙，卢立恒，等.地震动频谱特性对基础隔震结构双向地震响应的影响［J］.土木工程学报，2013，46（5）：50－55.Pan Y，Ji C L，Lu L H，et al.Effects of ground motion characteristics on bilateral seismic responses of baseisolated structures［J］.China Civil Engineering Journal，2013，46（5）：50－55.

［9］季晨龙.叠层橡胶支座基础隔震结构多维地震反应分析［D］.成都：西南交通大学，2012.

［10］北京金土木软件有限公司.SAP2000中文版使用指南［M］.北京：人民交通出版社，2010.

［11］GB 50011－2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.

［12］日本建筑学会.隔震结构设计［M］.刘文光.译.北京：地震出版社，2006：29.