无重访单亲遗传算法在配电规划中的应用

胡宇行，卫志农，孙国强，陈 婷，马骏毅

（1.河海大学能源与电气学院，南京210098；2.江苏镇江供电公司，镇江212000）

配电网规划是配电系统研究领域中的重要内容，其本质是一个非线性、高维数的复杂组合优化问题。目前，求解方法可分为解析式算法和启发式算法。解析式算法需要分析问题中各要素之间的关系，表示为函数表达式之后计算求解，这种方法可以得出最优解，但计算费时，只适用于解空间较小的优化问题；启发式算法虽然不能确定每次优化结果为最优，但可以在合理的时间内给出较优解，能够很好地适应大规模优化问题。启发式算法主要有遗传算法、蚁群算法、粒子群算法等。其中，遗传算法GA（genetic algorithm）是一种自适应随机搜索优化算法，GA 的遗传算子对基因进行随机操作，会产生不可行解，即孤网、环网等，故对这些不可行解的修复增加了GA 的计算量[1]。文献[2-3]提出并论证了单亲遗传算法PGA（partheno-genetic algorithm）的理论可行性和收敛性，指出采用新遗传操作方式可以快速高效地求解离散规划问题；文献[4-8]采用新型序号编码和遗传操作方式，即仅在一条染色体上进行全部遗传操作，将树的概念与PGA 相结合，对每个配电网的树形结构进行遗传操作，过程中不破坏配电网连通性和辐射性，有效地避免了孤网、环网等问题。但PGA 在遗传操作中会产生相当数量的重复解，增加了计算量，降低该算法的空间搜索效率。

为了避免重复解的产生，本文提出无重访单亲遗传算法NRPGA（non-revisit partheno-genetic algorithm），即在PGA 的基础上增加无重访环节，使得遗传操作产生的解不仅是可行的而且互不相同。算例测试表明，NRPGA 能够提高空间搜索效率，减少计算量，还可以提高最优解命中概率。

1 配电网网架规划模型

本文将配电网网架建设投资、运行费用、停电损失之和作为目标函数，该目标函数满足辐射状网架结构约束、线路电压降落约束、线路容量约束和待选线路约束等[9-12]。

1.1 目标函数

目标函数可表述为

其中：

式中：f1为配电线路建设成本，指铺设M 条线路的总投资；S 为按年度投资费用的现值之和折算的系数[12]；f2为配电网运行损耗成本，指把电网运行中线路上的有功损耗通过电价折算为费用；f3为配电线路故障停电成本，指把线路以一定的概率发生停电故障所造成的损失折算成费用；li为第i 条线路的长度；a 为单位长度架空线路价格；ΔPi为第i条线路上的有功损耗；t 为年最大损耗小时数[10]；β为电价（取居民生活用电电价）；λ 为单位长度线路故障率；t′为平均故障停电时间；Pi为流经第i 条线路的有功功率；R 为规划地区产点比；r 为折现率；T 为规划年限[12]。

1.2 约束条件

1）辐射状结构和连通性约束

配电网网架要保证连通性和辐射性，避免“孤网”与“环网”问题。

2）节点电压降落约束

式中：Vij为变电站节点i 与节点j 之间的电压降；Vm为节点i、j 之间的最大允许电压降。

3）线路容量约束

式中：Pij为节点i、j 的有功传输功率；Pm为节点i、j之间线路上允许的最大有功功率。

4）待选线路约束

式中：linei为在一次遗传操作中产生的第i 条线路；U 为在算例中提供的可选线路的集合；x1，x2，…，xn为可选线路。在16 节点算例中，给定U 含有28 条可选线路；在51 节点中，U 含有98 条可选线路。遗传操作产生的支路必须属于可选线路合集，并非任意两个负荷节点间都有可选支路。

2 无重访单亲遗传算法

2.1 基于树形结构编码方式的单亲遗传算法

配电网拓扑结构类似树，而单亲遗传算子对拓扑结构的操作实质上是改变配电网的树结构，即按照一定概率让处在不同层的节点互换。单亲遗传算子可分为移位算子和重分配算子。移位操作指在树的非负荷节点中随机选择一个移位点，断开其与父节点的联系，选择另一个节点作为其新父节点；重分配操作指随机选择重分配点，将以该点为根节点的子树中所有的节点进行重新分配。单亲遗传算子针对树结构进行操作，保证了树的辐射性和连通性。

2.2 无重访算法原理

在单亲遗传算法中，每次遗传操作产生一个种群A{X（1），X（2），…}。如果在这个种群中存在2 个染色体X（m）=X（n），说明解出现重复。重复解会增加不必要的计算量，从而影响空间搜索效率。本文引入无重访算法，使得每代遗传操作产生的种群中没有任何两个染色体是一样的，在代与代之间也没有任何两个染色体相同，这样保证了种群的多样性，减少不必要的计算量，提高空间搜索效率。

无重访算法依靠的是数据的快速查找，文献[13]基于二叉分割树（BSP tree）来实现无重访功能，并没有将该算法应用到配电网规划领域，而且该方法对空间分割的操作较为抽象，不能直观地表明各个可行解之间的联系。所以本文使用多叉树MS tree（multidimensional search tree）实现各新数据的快速查找与添加，避免了空间分割过程，使得无重访算法实现的过程简单、直观。MS tree 是一个高效的数据存储方式，当新数据产生时，使用这种存储形式进行查找能够快速地判断该数据是否与已知数据重复。基于多叉树的无重访算法原理如下。

图1 显示该多叉树已建立3 层，包含的元素分别为：0000，0001，0100，0200，0010，0110。0000为初始元素，0111，0110 为新产生的两个解。从第1 层第1 位开始往下逐一比较，如果数字相同，则比较下一层的下一位。可以发现新元素0111、0110与旧元素0100 的前两位相同，则移到与0100 相连的第3 层，发现0110 重复而0111 没有重复，所以加入0111 而删除0110，这样就完成了无重访的功能。结果如图2 所示。

图1 产生新元素Fig.1 Produce new elements

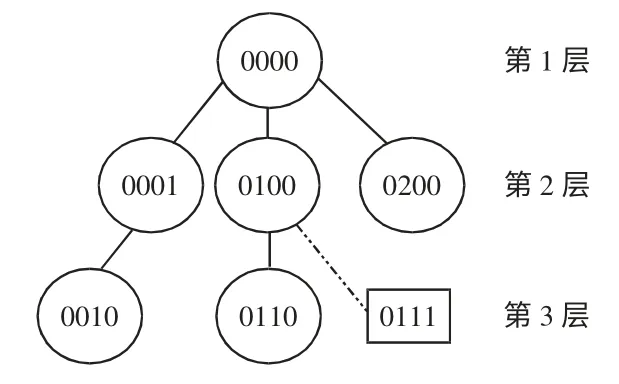
图2 加入新元素Fig.2 Add new element

2.3 无重访功能在配电网中的应用

将无重访遗传算法NRGA（non-revisiting genetic algorithm）应用于输电网络规划[14]，但NRGA 并不适用于优化配电网规划问题。因为NRGA 虽然避免产生重复解，但无法避免不可行解的产生。GA算法对各个基因进行遗传操作时，会随机地交换或变异个体基因的某部分，这一操作对生成的基因有明显影响，即GA 的遗传操产生的大量新基因并不符合配电网的基本约束条件，称为不可行解。对于这些不可行解，无论是修复还是舍去，都将造成计算量的显著增加，减少空间搜索效率。使用矩阵的形式存储配电网结构，可以快速判断并修复不可行解[15]。但约束条件不包括待选线路约束，任意两个负荷节点之间都可以连接，这使得搜索空间变大，而且不够贴近配电网规划实际情况。一旦增加了待选线路约束，则GA 算法所遇到的不可行解问题无法通过矩阵变换快速修复，失去了矩阵的优越性。所以，GA 不适用于优化带有特殊约束条件的配电规划问题。

为了适应配电网规划的特殊约束条件，快速求解优化问题，本文将无重访算法和PGA 相结合，提出NRPGA。本文采用树形结构存储配电网拓扑结构，在满足待选线路约束的条件下遗传操作时，可以直接对配电网的树形拓扑和父子节点进行重连，使得遗传操作既不产生重复解也不产生不可行解，NRPGA 避免了不必要的计算，能够有效提升空间搜索效率。

2.4 无重访功能实现流程

使用最小生成树算法产生初始解[13]，最小生成树是指从一个n 条带权无向完全图中选择n－1 条支路并使这个图仍然连通，同时考虑使树的权最小。常用Prim 算法和Kruskal 算法。设配电网有N个节点，M 条支路，无重访判别过程如下。

步骤1 产生初始解，并存入解结构体数组中。解结构体包括：说明配电网连接方式的一维数组A[M]（该数组中包含M 个二进制数，1 表示该线路连通，0 表示断开）和一个M 维的指针数组，作用是指向新的解结构体，并将所有不重复解结构体连接起来，建立了多叉树。将初始解结构体作为对比结构体。

步骤2 遗传操作产生配电网新解，存入新的结构体中。在算法收敛后，优秀基因种群中只含有少量不同解甚至只有一种解，对这些解进行多次遗传操作会遍历所有的可能解，程序进入死循环，因此设立一个足够大数MAX，当重复次数超过MAX 时，即使是重复解，也不再进行遗传操作。

步骤3 使用广度优先遍历对配电网新解的结构进行搜索，形成说明配电网连接方式的一维数组a[M]。

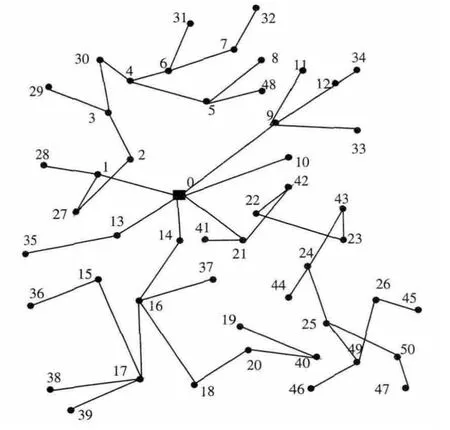
步骤4 比较新解数组a[M]与对比结构体数组A[M]。如果2 个数组在第k（0

步骤5 把新解的地址复制给该指针，退出程序。

步骤6 将步骤4 中第k 位指针所指向的结构体代替对比结构体。当kM 时，说明该解为重复解，退出程序。

2.5 无重访单亲遗传算法的实现步骤

设配电网有N 个节点，M 条支路，以线路建设成本、故障停电成本和运行损耗成本之和作为目标函数，使用无重访单亲遗传算法进行优化，流程如图3 所示。

图3 NRPGA 实现流程Fig.3 Flow chart of NRPGA

3 算例分析

使用PGA 与NRPGA 分别对不同的配电网算例进行优化，配电网算例模型参数见表1。进行200 次独立重复优化运算，记录并分析数据。

表1 模型参数Tab.1 Model parameters

3.1 16 节点配电网算例

图4 为16 个节点、28 条待架支路的10 kV 辐射型网络[16]。其中0～15 为各节点的编号，0 号节点为供电首端，带字母L 的节点为负荷点，其余为交叉节点，虚线为可以架线的走廊。

PGA、NRPGA 这2 种算法最终均能找到最优解，优化后的最小费用为81.75 万元。优化后的配电网网架结构如图5 所示。选取能够找到最优解的收敛过程为样本后取平均值，在16 节点算例中PGA 与NRPGA 的平均收敛过程如图6 所示。

图4 16 节点待规划配电线路Fig.4 Unplanned 16 pots distribution network

图5 优化后配电网线路示意Fig.5 Sketch map of 16 nodes planned distribution network

图6 16 节点中2 种算法收敛过程比较Fig.6 Comparison of PGA and NRPGA in 16 nodes

3.2 51 节点配电网算例

图7为一个51 个节点、92 条待架支路的辐射型网络，优化后的配电网网架结构如图8 所示。

优化后最小费用为301.4 万元。在51 节点算例中，操作方法与16 节点相同，PGA 与NRPGA 的收敛过程比较见图9。

3.3 PGA 与NRPGA 的比较

由于遗传算法的不确定，每次收敛过程和结果不尽相同。本文选取2 种算法都找到最优解的收敛过程为样本，取平均值，绘制成收敛过程图。

图7 51 节点待规划配电线路Fig.7 Unplanned 51 nodes distribution network

图8 51 节点优化后配电网线路示意Fig.8 Sketch map of 51 nodes planned distribution network

图9 51 节点中2 种算法收敛过程比较Fig.9 Comparison of PGA and NRPGA in 51 nodes

由图6 和图9 得出以下结论：

（1）随着配电网规模的增加，算法的搜索解空间变大，每次迭代找到最优解的概率变小，所以2种算法的平均收敛代数都明显增加；

（2）在不同规模的优化过程中，每次迭代后NRPGA 都找到了比PGA 更优秀的解。NRPGA 避免了遗传操作产生的重复解，相对于PGA，NRPGA收敛代数更小。由此，在增加无重访功能后，NRPGA 的空间搜索效率明显提高。

表2 和表3 分别为PGA 与NRPGA 这2 种算例优化过程中200 次独立重复实验的数据统计。

表2 16 节点算例中PGA 与NRPGA 的数据统计Tab.2 Statistics of PGA and NRPGA in 16 nodes

表3 51 节点算例中PGA 与NRPGA 的数据统计Tab.3 Statistics of PGA and NRPGA in 51 nodes

由表2 可知：①NRPGA 在寻找最优解次数占总实验次数比例上有非常明显的优势，即命中率高。在NRPGA 中，遗传操作产生的解是不重复的，所以NRPGA 有效地避免了早熟现象；②由于遗传操作方式的局限，PGA 在进行变异操作时不可避免地产生大量重复解，这些重复解会占据精英种群使得该算法出现早熟现象，影响了PGA 对解空间搜索的效率。

由表3 可知：①优化规模变大后，NRPGA 的最优解次数占总实验次数比例（即命中率）相应降低，但相对于PGA，命中率依然保持较大优势；②在51节点算例中，PGA 的命中率为2.5%，这说明大量的重复解占据精英种群导致了早熟现象。

对比表2、表3 可以发现：

（1）当算例规模变大后，遗传操作时各操作节点的可选节点变多，遗传操作产生重复解的概率下降，NRPGA 平均使用无重访功能的次数减少，由50 526.7 次下降为3 214.8 次。所以，随着搜索空间的变大，NRPGA 的命中率由88%下降为42%，无重访功能的效果下降。

（2）在2 个算例中，NRPGA 的命中率与PGA的命中率比值从4.4 上升为16.8，说明PGA 的命中率对搜索空间的大小更敏感，随着优化规模的增加，PGA 命中率从20%下降为2.5%。因此，在求解离散组合优化问题时，搜索空间越大，NRPGA 在命中率上的相对优势越明显。

（3）在2 个算例中，PGA 的平均收敛代数均比NRPGA 少，这是PGA 出现早熟现象的结果，不能说明PGA 在空间搜索效率上的优越性。

（4）在51 节点算例中，如果使用PGA 进行优化，在100 次独立重复运算后，优化后的解为最优解的概率为92%（1-0.975100）；而使用NRPGA 优化，在运算5 次后，就可以超过93%（1-0.585）的概率找到最优解。在实际运算中，NRPGA 有着巨大优势。

4 结语

本文将无重访功能和单亲遗传算法结合起来用以求解配电网网架优化问题。相比PGA，NRPGA不仅能够快速收敛，还能在遗传操作中保持种群的多样性，避免了早熟现象，从而提高空间搜索效率。测试表明，NRPGA 在大规模离散优化算例中有着较高的命中率，具有一定的工程实用价值。

[1]李茂军，童调生，罗隆福（Li Maojun，Tong Tiaosheng，Luo Longfu）.单亲遗传算法及其应用研究（Partheno-genetic algorithm and its application）[J]. 湖南大学学报（Journal of Hunan University），1998，25（6）：56-59.

[2]李茂军，童调生（Li Maojun，Tong Tiaosheng）.单亲遗传算法及其全局收敛性分析（A partheno-genetic algorithm and analysis on its global convergence）[J]. 自动化学报（Acta Automatica Sinica），1999，25（1）：68-72.

[3]李茂军，罗日成，童调生（Li Maojun，Luo Richeng，Tong Tiaosheng）.单亲遗传算法的遗传算子分析（Analysis on the genetic operators of partheno-genetic algorithm）[J].系统工程与电子技术（SystemsEngineeringandElectronics），2001，23（8）：84-87.

[4]陈婷，卫志农，吴霜，等（Chen Ting，Wei Zhinong，Wu Shuang，et al）. 考虑电动汽车充电站选址定容的配电网规划（Distribution network planning by considering siting and sizing of electric vehicle charging stations）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（3）：1-7.

[5]刘晓飞，彭建春，高效，等（Liu Xiaofei，Peng Jianchun，Gao Xiao，et al）. 基于单亲遗传算法的配电网络规划（Distribution network planning based on partheno-genetic algorithm）[J]. 电网技术（Power System Technology），2002，26（3）：52-56.

[6]麻秀范，崔换君（Ma Xiufan，Cui Huanjun）.改进遗传算法在含分布式电源的配电网规划中的应用（An improved genetic algorithm for distribution network planning with distributed generation）[J]. 电工技术学报（Transactions of China Electotechnical Society），2011，26（3）：175-181.

[7]章文俊，程浩忠，王一，等（ZhangWenjun，Cheng Haozhong，Wang Yi，et al）.基于树形结构编码单亲遗传算法的配电网优化规划（Distribution network optimal planning based on tree structure encoding partheno-genetic algorithm）[J]. 电工技术学报（Transactions of China Electotechnical Society），2009，24（5）：154-160.

[8]孔涛，程浩忠，李钢，等（Kong Tao，Cheng Haozhong，Li Gang，et al）.配电网规划研究综述（Review of power distribution network planning）[J].电网技术（Power System Technology），2009，33（19）：92-99.

[9]于会萍，刘继东，程浩忠，等（Yu Huiping，Liu Jidong，Cheng Haozhong，et al）.电网规划方案的成本效益分析与评价研究（Cost-benefit analysis and evaluation of power network planning）[J].电网技术（Power System Technology），2001，25（7）：32-35.

[10]陆广香，单渊达，龚乐年（Lu Guangxiang，Shan Yuanda，Gong Lenian）.最大负荷损耗小时数求取方法质疑（The method about the determination of maximum load′s loss hours is Doubtful）[J]. 电工技术学报（Transactions of China Electotechnical Society），1996，11（1）：55-59.

[11]苏海锋，张建华，梁志瑞，等（Su Haifeng，Zhang Jianhua，Liang Zhirui，et al）.基于改进均值聚类随机粒子群算法的变电站LCC 规划（Substation LCC planning based on refined mean clustering random particle swarm algorithm）[J].电工技术学报（Transactions of China Electotechnical Society），2012，27（4）：209-215.

[12]苏海锋，张建华，梁志瑞，等（Su Haifeng，Zhang Jianhua，Liang Zhirui，et al）.基于LCC 和改进粒子群算法的配电网多阶段网架规划优化（Multi-stage planning optimization for power distribution network based on LCC and improved PSO）[J].中国电机工程学报（Proceedings of the CSEE），2013，33（4）：118-125.

[13]Yuen Shiu Y，Chow Chi Kin. A genetic algorithm that adaptively mutates and never revisits[J].IEEE Trans on Evolutionary Computation，2009，13（2）：454-472.

[14]高元海，王淳（Gao Yuanhai，Wang Chun）. 无重访遗传算法及其在输电网络规划中的应用（Non-revisiting genetic algorithm and its application in transmission network planning）[J]. 中国电机工程学报（Proceedings of the CSEE），2011，33（4）：110-117.

[15]王方方（Wang Fangfang）.基于改进遗传算法的配电网规划（Distribution Network Planning Based on Improved Genetic Algorithm）[D].上海：上海交通大学电子信息与电气工程学院（Shanghai：School of Electronic Information and Electrical Engineering，Shanghai Jiao Tong University），2009.

[16]Jonnavithula S，Billinton R. Minimum cost analysis of feeder routing in distribution system planning[J]. IEEE Trans on Power Delivery，1996，11（4）：1935-1940.