邻接矩阵和粒子群优化算法应用于微电网重构

辛文成，向铁元，詹 昕，贺忠尉，陈 浩，苏井辉

（武汉大学电气工程学院，武汉430072）

近年来，随着电网规模的逐渐扩大，现有的大规模互联电力系统的弊端逐步出现，例如运行控制复杂，安全性和可靠性偏低等。特别是近几年世界范围内的几次大停电事故，引发了人们对庞大电网建设的反思，也掀起了微电网研究的热潮[1-5]。微电网是指由微型电源、负荷和临近终端的用户共同组成的系统。由于微电网临近用户终端，所以有闭环设计开环运行的特点，在系统发生故障时，微电网迅速重构，可以孤岛运行或并网运行，起到保障重要负荷持续供电或支援大电网恢复的作用。微电网重构，实际上就是调整线路的分段开关和联络开关，改变网络的拓扑结构，在一定的约束条件下使某一指标最优，如负荷损失最小或网损最小等等。因此微电网重构是典型的带约束的非线性组合优化问题。在微电网中虽然用0、1 表示开关的状态很合适，但作为优化变量的开关数量众多，当有n 个开关时，将会有2n种不同的状态组合，很容易出现维数灾的问题。如果单纯地用粒子群算法[6-7]、遗传算法[8-9]等智能算法将会产生大量的随机树状结构，形成很多不可行解，并且计算时间较长，迭代次数也较大。

基于上述问题，本文提出了一种基于邻接矩阵和粒子群优化的混合算法。通过网络的邻接矩阵，能较好地进行前推回代潮流计算，还能对系统结构进行筛选，排除了不满足网络条件的环型网络和不满足潮流约束的拓扑结构，然后运用粒子群算法进行寻优，较好地解决了上述问题，具有一定的实用价值。

1 微电网重构与配电网重构的区别

微电网是一个比较新的概念，综合了分布式发电技术、电力电子技术和储能技术，其主要组成部分包括微电源（分布式电源）、储能装置、负荷和管理系统。微电网原型采用美国电气可靠性技术解决方案联合会CERTS（consortium for electric reliability technology solutions）推荐模型，如图1 所示。

图1 微电网原型Fig.1 Micro-grid prototype

图中，微电网采用馈线式网络，对电能质量需求不同的负荷分线供电，在不同的负荷区之间采用不同的潮流控制器隔离。微电网在发生重构过程时关注的问题与传统的配电网关注的问题不同，具体体现在以下3 个方面。

（1）微电网的网络结构由传统的单端母线供电的辐射状网络变成一个多电源和多用户的复杂网络。馈线上的潮流大小和方向不固定，而且随时具有较大的变化，因而微网在重构过程中的潮流计算具有动态的特点。

（2）由于微网本身具有频率调节能力及电压调节能力，因此既能与电网并联运行，又能孤岛运行。当大电网发生故障时，微电网还可以作为备用电源，帮助大电网恢复供电。

（3）面向用户是微电网最重要的设计原则，因此微电网在发生故障重构时重视保负荷，应依据负荷的重要程度与微电网的具体情况，确定是保、切还是调，合理进行负荷控制。这一点与传统配电网在故障时保护大电网是不同的。

综合以上分析可以看出，微电网重构与配电网重构存在较大的差别，应该根据微电网这些独有的特点，合理选择重构方式。

2 微电网重构数学模型

微电网在故障情况下的重构是一个考虑多种约束情况下的非线性组合优化问题。

2.1 目标函数

以负荷损失最小为目标函数，并且尽可能地保证对重要负荷供电，即

式中：kl为负荷l 的权重系数，指每停运单位MW电量的赔偿价格，价格差别[10]是由负荷类别不同导致的；Pl为负荷l 的有功；N 为用户所在的区域；t为0 或1，代表负荷被切或者被保留。微电网在重构完成后经济赔偿为最小，其中价格赔偿矩阵为

kl=[0，2 000，0，1 600，2 500，3 000，3 700，0，3 100，100 000，7 000]，其中，0 表示微电源或没带负荷的节点。

2.2 约束条件

微电网故障恢复重构策略一般需要考虑潮流约束、节点电压约束、有功平衡约束、支路容量约束和网络结构约束。

1）潮流约束

由于微网特殊的拓扑结构，常规的潮流算法，如PQ 分解法不适合求解，本文采用前推回代法[11-12]，Matlab 编程实现。根据潮流的不确定性，将负荷功率用正负来区分，即

式中：Ui、Pi、Qi分别为节点i 的电压、有功注入量和无功注入量；N 为系统总的节点数。

2）节点电压约束

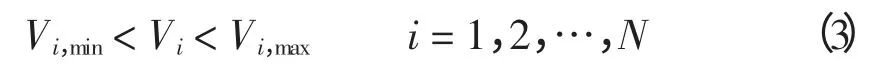
式中，Vi，min和Vi，max分别为节点i 的电压最小和最大允许值。

3）有功平衡约束

将有功功率约束简化为频率约束，即

式中：ΔP 为微网总的有功缺额；Δf 为微网频率变化；kf为频率调节系数，在微网中取1.2。当判断损失的ΔP/kf大于0.2 Hz 时，将不进入潮流计算程序，继续改变网络结构。

4）支路容量约束

式中：Sn为支路n 传输的功率；Sn，max为支路n 允许传输的最大功率；L 为重构后微网的支路数。

5）网络结构约束

微电网直接面向用户，一般闭环设计开环运行，因此微电网的拓扑结构一般为辐射状，即

式中：m 为故障重构后的网络结构；MR为所有可能的辐射状网络。

3 邻接矩阵和粒子群混合算法在微网重构中的应用

3.1 邻接矩阵算法

邻接矩阵是网络结构中表示节点与节点之间拓扑关系的矩阵。设网络节点数为n，则邻接矩阵为n 阶方阵，其中行与列对应于节点。矩阵元素定义如下：如果节点j 与节点i 相连接则矩阵元素为1，如果节点j 与节点i 不相连接则矩阵元素为0，即

据此将图1 简化等效，如图2 所示。则邻接矩阵为

11 × 11 阶邻接矩阵D 代表着图2 中的11 个节点，矩阵中为“1”的点可用变量kki（数值为0 或1）来代替，以改变网络结构。完整的邻接矩阵是对称阵，为了存储方便，在编程时用上三角形矩阵或下三角形矩阵来存储。根据邻接矩阵中的“0”“1”关系，用程序寻找出网络是环型还是辐射型，进而排除环型网络，使程序不进入粒子群寻优，减少运行时间及迭代次数，为微电网重构奠定基础。

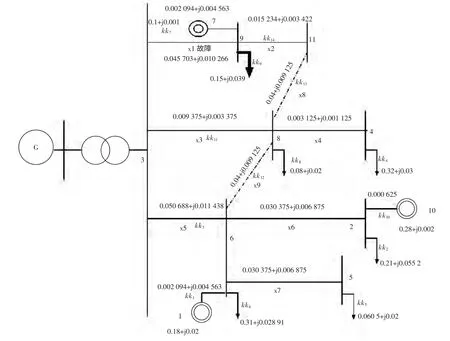
图2 微电网重构算例Fig.2 Micro-grid reconfiguration results figure

3.2 粒子群算法

粒子群算法是由Eberhart 和Kennedy 提出的一种生物群体智能演化算法。种群的每个粒子能够表示成某目标函数的可能解并有其适应值，并且个体粒子xid的位置状态用0 或1 表示，速度vid用来表示粒子位置状态变化的概率，迭代公式为

判断个体粒子xid位置状态的更新公式为

3.3 微电网重构求解

微电网重构算法步骤如下。

步骤1 设置种群大小Z、最大迭代次数count，粒子维数kk、惯性权重系数w 和加速系数c1、c2、vi等参数。

步骤2 建立带开关序列的微电网邻接矩阵，即将矩阵D 中为“1”的元素变为kki，同时将微电网中的负荷和微电源都乘以kkj。kki、kkj的状态位置0 和1 代表负荷或线路的“连接”和“断开”。

步骤3 随机初始化粒子群得到Z 个可行解kki，i=1，2，…，Z。利用邻接矩阵筛选掉不符合条件的解，然后将这些解代入前推回代潮流程序中计算，在前推回代计算时，要时刻注意切负荷后ΔP/kf（即Δf）的变化，将之作为进入前推回代的一个判断条件，同时算出每个可行解kki的适应度，将其作为个体粒子的历史最优适应度Pbest，j，而当前全局最优解Pbest，g为所有个体最优解中的最小值。

步骤4 根据式（8）、式（9）对粒子的位置状态kki和粒子的速度vi进行更新，算出更新开关位置状态后kki的适应度值。

步骤5 如果粒子kki的适应度优于当前个体最优解Pbest，j，则将其值赋给Pbest，j。若最佳Pbest，j优于全局最优Pbest，g则将Pbest，j赋给Pbest，g。

步骤6 判断迭代次数是否大于count。若大于则停止计算；否则转到步骤4。

根据以上步骤即可求出目标函数的最优解。

4 算例分析

将微电网原型[13]简化，如图2 所示，图中数字1、7、10 为微电源，线路上复数值为阻抗值，节点复数值为功率值。设线路3-7 故障，微电源模型的输出功率值可变，即为PQ 模型。设粒子群规模为100，最大迭代次数为100，常数c1、c2为2。Matlab编程，最终算出微网所保留的总负荷为0.19 +j0.120 1 p.u.，总经济赔偿为742.2 元。有无邻接矩阵的算法迭代曲线如图3 和图4 所示，所得出的潮流和开关序列如表1 和表2 所示。

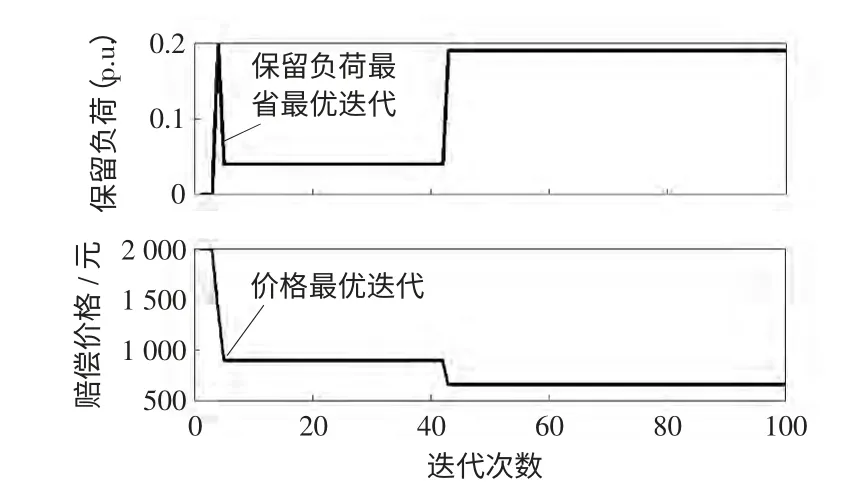
图3 算法迭代曲线（有邻接矩阵）Fig.3 Curves of iterative algorithm with adjacenay matrix

图4 算法迭代曲线（无邻接矩阵）Fig.4 Curves of iterative algorithm without adjacency matrix

表1 最优开关序列Tab.1 Optimal switch sequence value

表2 与最优开关序列值对应的潮流Tab.2 Power flow related to optimal switch p.u.

将表1 的开关序列结果同文献[13]相比较，可以看出两者的最优开关序列一致，即备用线路8-11 投入运行，节点4 和节点5 的负荷被切掉；由表2 的潮流可以看出，微网节点电压、线路功率损耗以及支路传输的功率都较好地满足了潮流要求，此算法是可行的；将图3 与图4 比较得知，有邻接矩阵算法迭代次数比没有邻接矩阵时迭代次数少100 多次，收敛速度快。

5 结语

微电网独有的运行特点决定了微电网重构不同于传统电网重构，本文利用邻接矩阵和粒子群优化混合算法较好地解决了微电网重构问题。算例结果表明，该算法具有很好的可行性和准确性，并且收敛速度较快，对提高微电网的可靠运行和经济性有积极作用。

[1]鲁宗相，王彩霞，闵勇，等（Lu Zongxiang，Wang Caixia，Min Yong，et al）.微电网研究综述（Overview on microgrid research）[J].电力系统自动化（Automation of Electric Power Systems），2007，31（19）：100-107.

[2]Phillips L R. Tasking and policy for distributed microgrid management[C]//IEEE Power Engineering Society General Meeting.Tampa，USA：2007.

[3]Lasseter R H. Microgrids[C]//IEEE Power Engineering Society Winter Meeting.New York，USA：2002.

[4]苏玲，张建华，王利，等（Su Ling，Zhang Jianhua，Wang Li，et al）.微电网相关问题及技术研究（Study on some key problems and technique related to microgrid）[J]. 电力系统保护与控制（Power System Protection and Control），2010，38（19）：235-239.

[5]马力（Ma Li）. 混合系统微网控制策略分析（Control strategy analysis of hybrid system in micro-grid）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（6）：104-108.

[6]靳晓凌，赵建国（Jin Xiaoling，Zhao Jianguo）. 基于改进二进制粒子群优化算法的负荷均衡化配电网重构（Distribution network reconfiguration for load balancing based on improved binary particle swarm optimization）[J].电网技术（Power System Technology），2005，29（23）：40-43.

[7]李越，王丰华，金之俭，等（Li Yue，Wang Fenghua，Jin Zhijian，et al）.基于粒子群和人工免疫融合算法的接地网优化设计（Optimization design of grounding system based on the particle swarm and artificial immune algorithm）[J].电力系统保护与控制（Power System Protection and Control），2011，39（15）：120-126.

[8]余贻鑫，段刚（Yu Yixin，Duan Gang）.基于最短路算法和遗传算法的配电网络重构（Shortest path algorithm and genetic algorithm based distribution system reconfiguration）[J].中国电机工程学报（Proceedings of the CSEE），2000，20（9）：44-49.

[9]刘蔚，韩祯祥（Liu Wei，Han Zhenxiang）.基于最优流法和遗传算法的配电网重构（Distribution network reconfiguration based on optimal flow pattern algorithm and genetic algorithm）[J]. 电网技术（Power System Technology），2004，28（19）：29-33.

[10]方向晖.中低压配电网规划与设计基础[M].北京：中国水利水电出版社，2007.

[11]颜伟，刘方，王官洁，等（Yan Wei，Liu Fang，Wang Guanjie，et al）.辐射型网络潮流的分层前推回代算法（Layer-by-layer back/forward sweep method for radial distribution load flow）[J].中国电机工程学报（Proceedings of the CSEE），2003，23（8）：76-80.

[12]王峥，从培杰（Wang Zheng，Cong Peijie）.基于改进前推回代法的辐射状配电网潮流计算（Power flow calculation for radial distribution network based on forward and backward substitution method）[J].东北电力技术（Northeast Electric Power Technology），2008，29（2）：7-10.

[13]乔颖，鲁宗相，毛延斌，等（Qiao Ying，Lu Zongxiang，Mao Yanbin，et al）. 微电网在灾难性事故中的系统重构（Reconfiguration of microgrid in the catastrophy）[C]//可靠性市供电专委会学术年会.北京，中国：2008.