立式低温储罐的实体模型简化分析

张 为，李 晶

(长春理工大学机电工程学院，吉林长春130022)

随着国内乙烯装置的不断扩大和增加，以及沿海地区液化石油气、天然气的储存规模和需求的增大，对于低温储罐的需求和大

型化的要求也日益增长［1］.从立式低温储罐的结构特点［2-3］上可以看出，横向地震载荷作用时，低温储罐主要承受载荷部件为径向拉带，由于径向拉带是沿着罐体中心轴环向布置，这就有可能使拉带产生压缩失稳，拉带失稳之后就会影响分析结果的真实可靠性.本文就是针对以上问题提出对两种结构进行对比分析，此两种结构分别为不考虑径向拉带压缩失稳结构和考虑径向拉带压缩失稳结构.同时本文采用实体建模［4］，达到了建模简单，修改容易的参数化效果.

1 立式低温储罐的整体结构

立式低温储罐的整体结构及实体模型如图1所示.

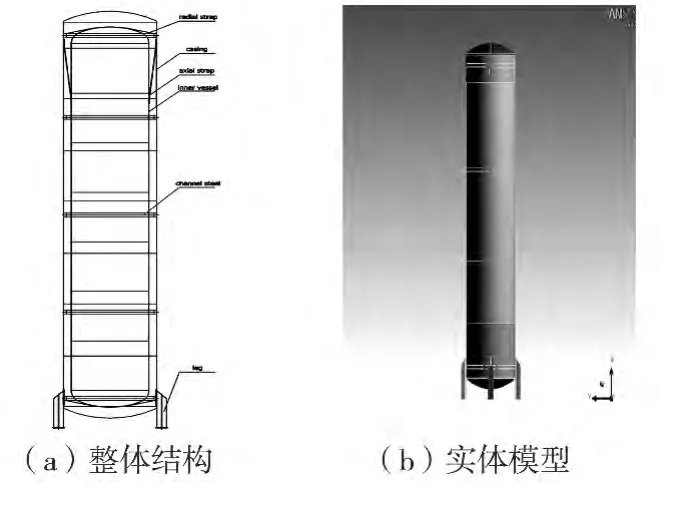
图1 立式低温储罐的整体结构及实体模型

储罐总高为13.818 m，外筒外径为3 m，厚度为9.4742 mm，材料为Q235-B;内筒体外径为2.5 m，厚度为9.35 mm，材料为 1.430 1(欧盟钢材牌号);内筒体和外筒体由16径向拉带(上下各8个均匀分布在内筒体封头上)和4个沿着内外筒夹套之间周向均匀分布的轴向拉带连接.

径向拉带的宽度为101.6 mm，厚度为12.7 mm，材料为0Cr18Ni9［5］;轴向拉带宽度为 120 mm，厚度为19 mm，材料为0Cr18Ni9;为保证外筒体的稳定性［6］，沿着外筒体轴向设有5个均匀分布的加强圈［7］;整体结构由四个支腿支撑.

2 有限元分析

2.1 有限元几何模型建立

本文采用三维实体模型软件［8］creo1.0建立立式低温储罐实体模型，应用有限元分析软件workbench进行有限元分析［9］.由于该总体结构用实体建模，同时还具有薄壳体征，因此采用solidshell单元进行网格划分和结构分析.

为了对比起见，文中分析了两种不同结构形式的立式低温储罐，分别为不考虑径向拉带压缩失稳结构和考虑径向拉带压缩失稳结构.

2.2 径向拉带压缩失稳实验

压缩失稳［10］即薄板在压缩变形过程，失去了保持其原来平面形状的能力而产生弯曲隆起的现象.压缩失稳的根本原因是压应力的存在和弯曲(有的伴随着扭转)的出现.压缩失稳的特征，以无限制的继续弯曲(或加上扭转)来说明.由此可以看出，当结构受地震载荷时有些径向拉带可能会产生失稳，失稳之后的径向拉带失去了原来的作用，严重时可能会影响软件分析结果，导致应力不真实性使结构失效.所以在考虑径向拉带压缩失稳结构中，要先进行拉压测试，经过测试结果，得出上下封头上各5个拉带受压，即去掉这10个径向拉带.

2.3 理论验证

对于细长受压杆件，当压力较小时，构件能保持原有的直线平衡状态;若压力增大到某一数值时，构件会突然变弯，使结构不能正常工作，这种现象称为丧失稳定［11］.

压杆类型判定依据见表1.

表1 压杆判定依据

其中:

E表示材料弹性模量(不锈钢为2×105MPa);λ表示压杆柔度;a，b表示直线经验公式系数;σs表示材料的屈服强度;σp表示材料的比例极限(不锈钢为30.1);μ表示压杆的长度因数(见表2);

表2 压杆的长度因数μ

在本文中，径向拉杆形状及与内外筒体连接位置如图2所示.

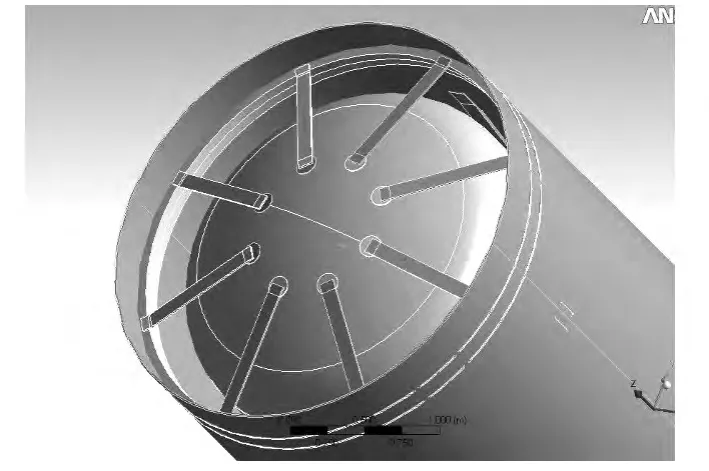
图2 径向拉杆形状及与内外筒体连接位置

其简化情况如图3所示，其中径向拉杆长l为 998.65 mm，宽 h 为 101.6 mm，厚度 s为12.7 mm.

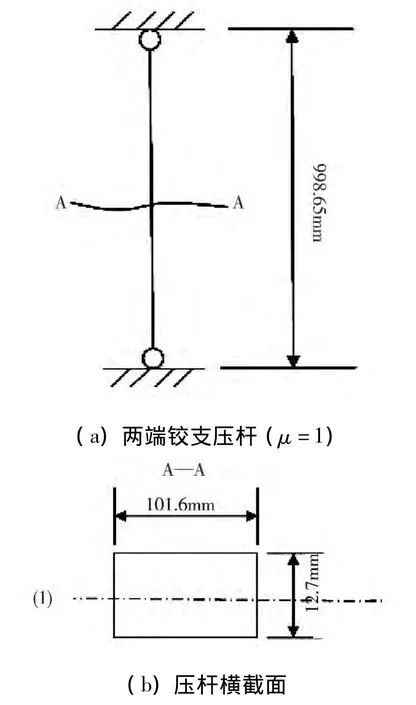
图3 径向拉杆简化图

通过计算得:

柔度极限:从保守的角度来看，本计算中选择第一种情况下的惯性矩，即选取I(1)来计算惯性半径.

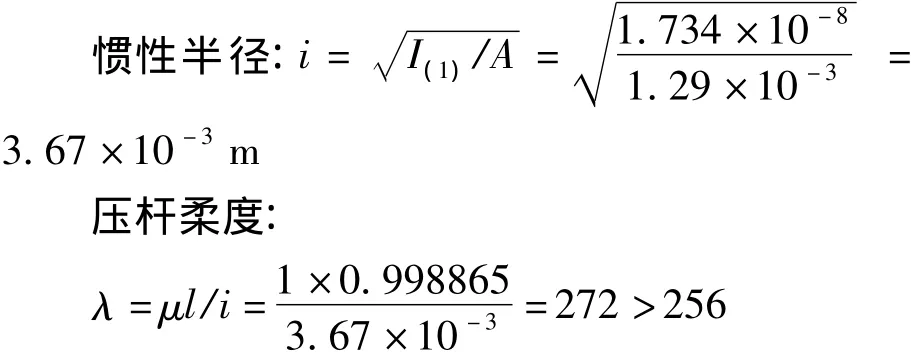
根据表1可知，该压杆为大柔度压杆，所以根据欧拉公式得:

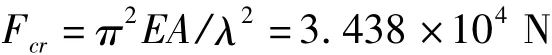
根据图2径向拉杆形状及与内外筒体连接位置将径向拉杆受力情况简化成如图4所示.已知内筒受力 F内=4.983×105N，外筒 F外=1.3282×105N，即合力.

图4 径向拉杆受力简图

由受力方向可知，受力为 F1，F2，F3，F4，F5的杆件为受压杆件，经给出的数据计算可得:

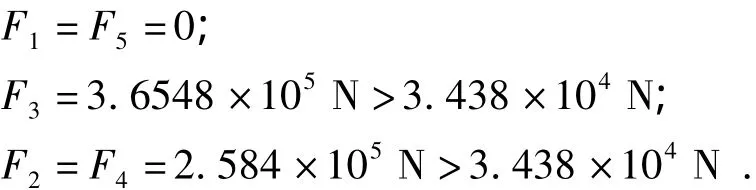
所以在计算过程中，考虑压杆失稳的影响，将受力为 F1，F2，F3，F4，F5的杆件去掉.通过该理论计算结果验证了上述拉压测试的正确性，可以用该简化方法进行下一步的模拟计算.

2.4 载荷与边界条件

外筒体加外压 0.1 MPa，垂直地震力［12］1 070 327.4 N，水平地震力631374.9 N.边界条件是在储罐的4个支腿处加全约束.加载形式如图5所示.

图5 两种结构加载方式

2.5 结果分析

由于图5的加载方式主要就是校核径向拉带与外筒体连接部位的应力，所以图6给出了两种结构外筒体的等效应力分布.

图6 两种结构的等效应力分布

不考虑径向拉带压缩失稳结构的等效应力为121.79 MPa，考虑径向拉带压缩失稳结构的等效应力为141.4 MPa，压缩失稳影响因素达到16%，此数值超过了允许范围(即5%以内).因此可以得出此种简化考虑的正确性，对于储罐实体结构分析考虑压缩失稳是十分重要的.

3 结 论

本文在分析储罐实体模型的基础上得出了一种新的简化分析方法，突出了压缩失稳在这类立式低温储罐结构分析中对其结果的影响，同时表明了三维实体软件中实体模型导入有限元分析软件的可行性，此种简化方法不仅使分析结果更趋于实际情况，也更能确定得出的等效应力能够满足结构的强度要求.

［1］ 阚红元.大型立式圆筒形低温储罐简介［J］.石油化工设备技术，2007，28(5):24-27.

［2］ 王旭，唐潇南.关于低温液体储罐设计有关问题的探讨［J］.石油和化工设备，2008，11(2):19-21.

［3］ 庞法拥，林树彦.浅淡大型低温储罐的设计［J］.化学工程与装备，2011(12):69-70.

［4］ 毛雪东，张杰.基于实体模型的低温液体储罐有限元结 构 分 析［J］.化 工 学 报，2010，61(5):1107-1111.

［5］ 王萌，巩建鸣.奥氏体不锈钢低温气体渗碳工艺研究现状［J］.压力容器，2012，29(6):45-48.

［6］ 张艳春，于国杰，杜国强，等.LNG大型低温储罐加强圈设计［J］.石油与天然气化工，2011，40(5):433-436.

［7］ 詹友刚.Creo1.0快速入门教程［M］.北京:机械工业出版社，2012.

［8］ YAN Yu，WANG Hai-bo.Prediction of stiffener buckling in press bend forming of integral panels［J］.Transactions of Nonferrous Metals Society of China，2011，21(11):2459-2465.

［9］ 冷纪桐，赵军.有限元技术基础［M］.北京:化学工业出版社，2010.

［10］李金科，张贤福.外压圆筒的计算及数值计算稳定性分析［J］.压力容器，2011，28(7):35-39.

［11］闫晓鹏，武瑛.材料力学［M］.北京:清华大学出版社，2012.

［12］杜英军，谢根栓.Ansys软件在化工设备抗震中的应用［J］.化工设备技术，2005，26(6):71-73.