具有马尔可夫性的HJM模型下的广义久期

薛冬梅，刘 巍

(吉林化工学院理学院，吉林吉林132022)

利率是金融市场上最重要的价格变量之一，它直接决定了相关金融产品的定价和利率风险的管理.HJM模型是描述利率随机行为的连续时间模型，由Heath，Jarrow，Morton于1992年在其发表的论文《债券定价及期限结构:一种新方法》［1］中所提出.它的新颖之处在于:直接从远期利率期限结构的跨期波动特征入手，设定债券和相关衍生品在有效期内的波动率函数结构，以整条收益率曲线作为状态变量，根据给定的初始远期利率曲线精确拟合当前的各种远期利率曲线，已成为嵌套所有利率期限结构模型的一致框架［2］.

由于久期作为利率风险管理的重要工具，可以准确、有效地衡量利率水平对债券价格的影响，因此为了更好地在利率风险管理中实施有效的风险控制策略，本文研究了具有马尔可夫性的HJM模型下的广义久期.

1 HJM模型概述

考虑市场行为在有限时间间隔［0，τ］内发生，市场信息的到达可由一个完备过滤概率空间(Ω，F，P)获得，其中Ω是状态空间，F是可测事件的σ－代数，P是概率测度，完备过滤结构{Ftt∈［0，τ］}由n≥1个初始值为0的独立标准布朗运动Wi(t)，1≤i≤n生成.

1.1 风险中性的单因素HJM模型

令r(t)表示t时刻当期的瞬时远期利率，对所有的t∈［0，τ］，有r(t)=f(t，t).

对每一个T≤τ，HJM(1992)利用代表远期利率运动的随机过程族描述了利率期限结构的动态，远期利率动态的积分形式为:

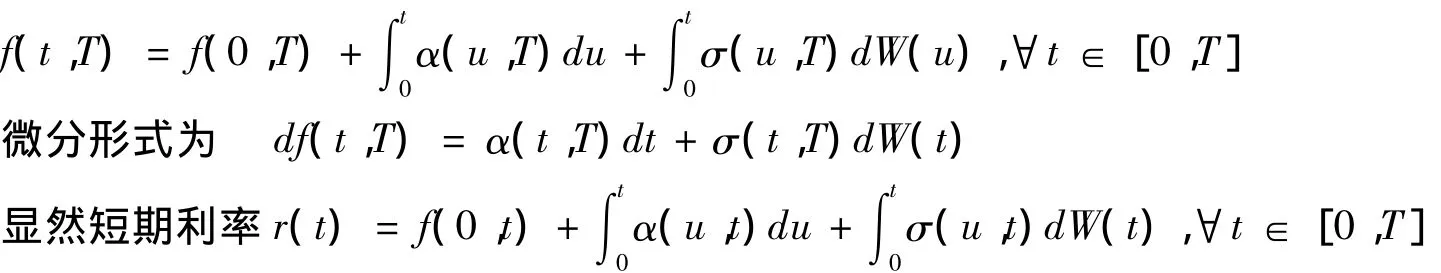
这里α:［0，t］×Ω→R是瞬时漂移率，σ:［0，t］×Ω→Rn是到期日为T的远期利率在时刻t时的

瞬时波动率.W是一个n维标准布朗运动，过程α与σ分别是R和Rn上的适应过程.引理1 在上面的条件下，无套利零息债券价格过程为

值得注意的是，整个模型估计的参数只有一个，即波动性，而且这个波动性不会随测度的变化而变化，它表明我们可以通过测量波动率并与短期利率相匹配，利用模型求出债券价格及远期利率等.

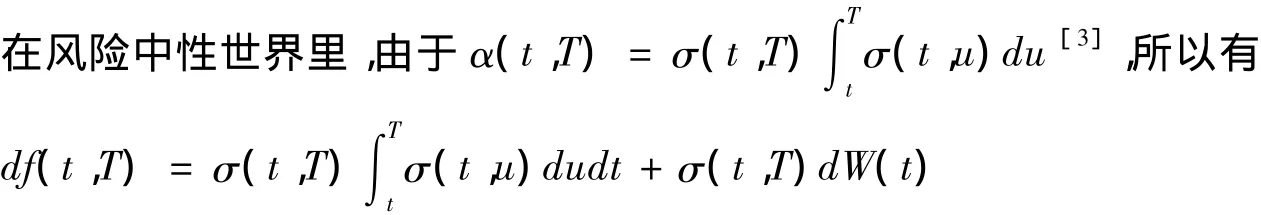
1.2 风险中性的n因素HJM模型

前提条件不变，此时瞬时远期利率过程假定满足随机积分方程满足:

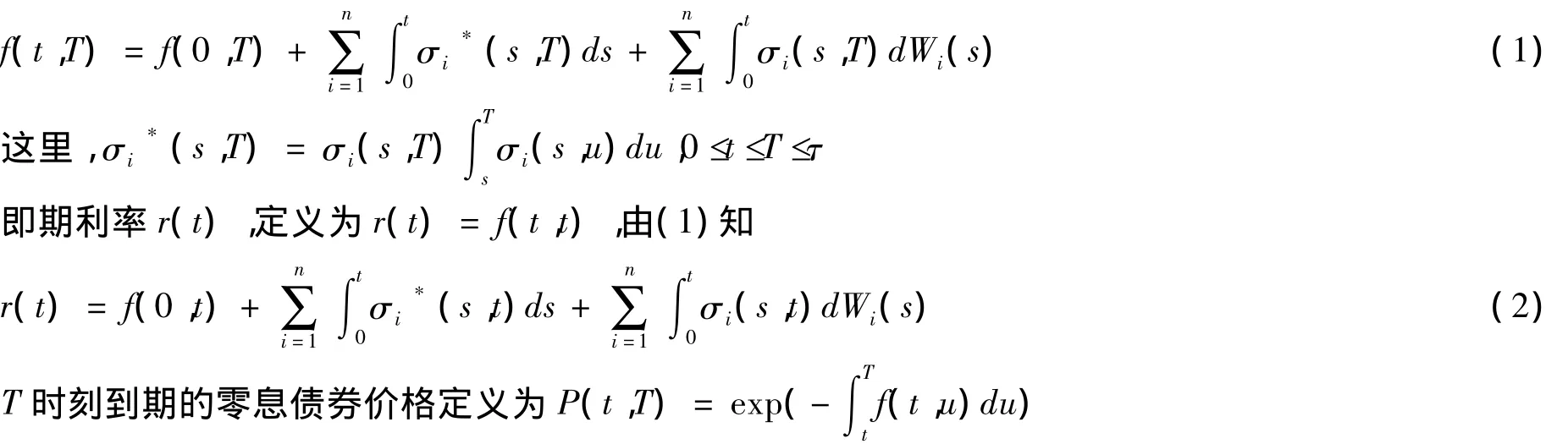
则(1)及(2)的微分形式为

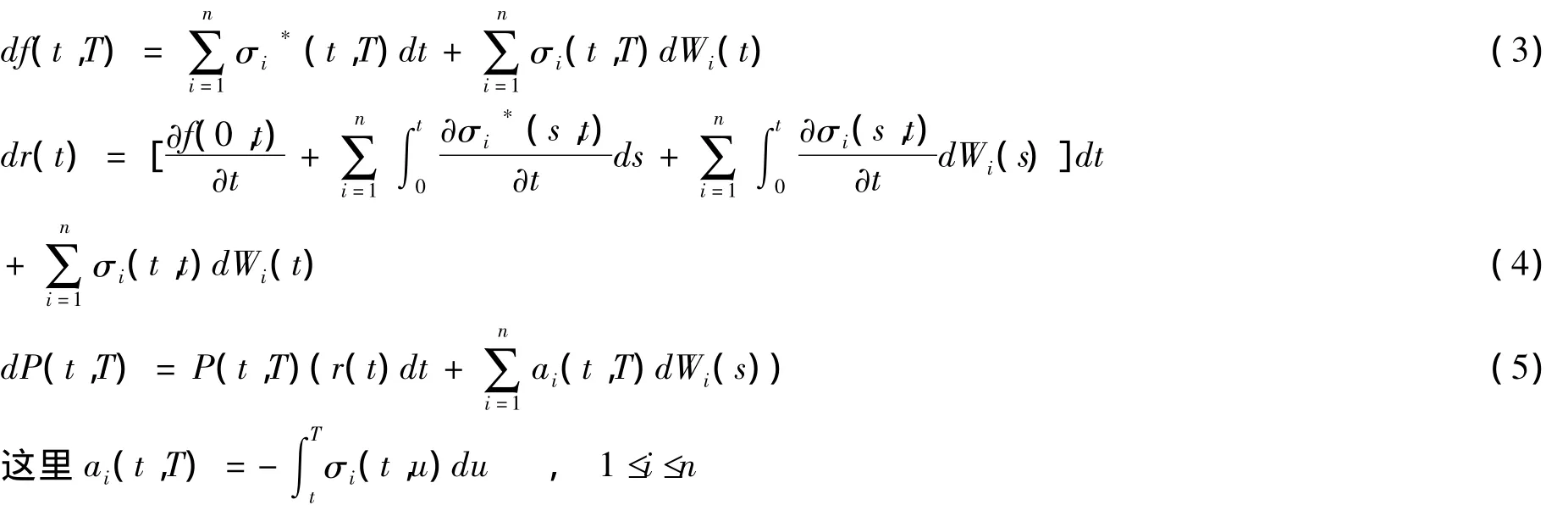
1.3 具有马尔可夫性的HJM模型

在一般意义上讲，HJM中蕴涵的r(t)不仅仅取决于t，而且还依赖于收益率曲线从0至t时刻的全部历史(the whole history of the yield curve up to that time)，也就是说，r(t)不具备马尔可夫性［4］.

2 具有马尔可夫性的HJM模型下的广义久期

2.1 久期

在1938年的一份研究报告中，弗里德里克﹒麦考利(Frederick Macaulay)创造性地提出了久期(Duration)的概念.它是债券风险度量中一个重要的特征参数.

久期可定义为债券的所有现金流量发生时间的加权平均值.权重根据各现金流对总体债券价值的重要性来确定.具体地讲，权重可以表示为某现金流量的现值与债券价格的比值.以CFt代表t时的现金流，Wt代表权重，则有

因为债券价格P是所有现金流量的现值的总和，所以Wt也可表示成，很显然，所有权重的总和为1.0.这样债券的久期D就可以用下式来表示:

2.2 广义久期测度

息票债券的久期测度被定义为与息票债券具有相同瞬时方差的零息债券的到期时间［8］.考虑一个在tj，(j=1，2，…，N，t＜t1＜… ＜tN)支付Cj单位账户的自由违约息票债券，在无套利机会的条件下，时刻t的债券价格为

对单因子模型可以简化为:

2.3 应用

3 结 论

本文介绍了具有马尔可夫性的HJM模型，在此框架下引入了广义久期测度，介绍了广义久期在波动结构确定的HJM模型中的应用，并给出了它们的解析解.

［1］ Heath D.，Jarrow R.，Morton A..Bond Pricing and The Term Structure of Interest Rates:A New Methodology for Contingent Claims Valuation［J］.Econometrica，1992，60(1):77-105.

［2］ 孙大鹏，汪波.HJM框架下利率风险测度的随机久期和凸度研究［J］.西安电子科技大学学报(社会科学版)，2007，17(5):45-49.

［3］ Carl Chiarella，Oh Kangkwon.Class of Interest Rate Models under the HJM Framework［J］.Asia-Pacific Financial Market，2001，8:1-22.

［4］ 徐景峰，于谨.利率与寿险产品定价研究［M］.北京:中国财政经济出版社，2004.

［5］ Carl Chiarella，Oh Kangkwon.A Complete Markovian Stochastic Volatility Model in the HJM Framework［J］.Asia-Pacific Financial Market，2000，7:293-304.

［6］ Carverhill，A.When is Short Rate Markovian［J］.Mathematical Finance4，1994，4:305-312.

［7］ Bhar R，Chiarella C.Transformation of Heath-Jarrow-Morton Models to Markovian Systems［J］.European Journal of Finance，1997，3:1-26.

［8］ Munk C.Stochastic Duration and Fast Coupon Bond Option Pricing in Multi-Factor Models［J］.Oden University，Working Paper，1998.

［9］ 龚光鲁.随机微分方程引论［M］.北京:北京大学出版社，1995.

［10］ Jian Zhihong，Li Chulin.Generalized Stochastic Duration in Markovian Heath-Jarrow-Morton Framework［J］.数学物理学报，2002，22B(1)，99-106.