基于持续期模型对高频金融数据分析

钱有程，王 暘

(1.吉林化工学院理学院，吉林吉林132022;2.商务部国际贸易经济合作研究院，北京100710)

高频金融数据是指在细小的时间间隔上抽取的金融交易观测值.数据的获得与处理方法的发展，使得高频数据的获取成为现实，并且受到微观市场研究者的广泛关注［1］.

Cho，Russell，Tiao，和 Tsay(2000)利用在台湾股市交易所中交易的340多只股票在一天中的每5分钟的收益率，研究设定日股价上下限的影响，发现了向股价上限趋近磁效应的显著证据［2］.

同时，高频数据还有一些低频数据不会出现的独特特征.本文中，我们主要研究这些特殊的特征，考虑分析高频数据的方法，并且讨论所得结果的应用.本文利用持续期模型对中国石油2014年6月9日至6月18日8个交易日1分钟高频交易数据进行分析及其应用.

1 高频数据及其模型

高频数据具有一些低频数据不会出现的独特特征，从而，对于这些数据的分析给金融经济学家统计学家提出了新的挑战.

1.1 非同步交易

不同的股票有着不同的交易频率，交易并不是同时发生的;即便是同一种股票，其交易强度也是一小时一小时地、一天一天的变化的.对于日序列，股价指的是其收盘价格.如果我们假定日收益率序列在24小时里是等间隔的往往是不正确的.实践证明，即使是在真实的收益率序列是前后独立的时候，这种假定可以导致股票收益率可预测性的错误的结论.

对于股票日收益率，非同步交易可以导致股票收益率之间的一步延迟交叉相关，组合收益率的1步延迟序列相关，以及在某些情形下，单只股票收益率序列的负序列相关.

1.2 买卖报价差

以标价Pb购买，以更高的叫价Pa卖出(对公众来说，Pb是卖出价格，Pa是买入价格).

1.3 交易数据的经验特征

不等间隔的时间区间:交易(如交易所里面的股票交易)不是在等间隔的时间区间上发生的.

日周期或者日模式的存在:在正常交易条件下，交易活动能够展示周期模式，交易之间的时间持续期亦呈现日循环模式.

此外高频数据还具有一秒钟多重交易的特性.

1.4 持续期模型

持续期模型是研究交易之间的间隔.较长的持续期预示着较少的交易活动，反过来表明了一个没有新消息的时期.日内交易展示了一些日模式.因此，我们集中讨论调整的时间持续期

我们运用简单的二次函数与示性变量来处理日交易活动中确定的组成部分.

1.5 ACD模型

自回归条件持续期(ACD)模型利用GARCH模型的实现来研究方程(1)中调整的时间持续期的动态结构.为了记号的简便，定义xi=.

2 对中国石油数据的实证分析

数据来源于证券之星网站的分钟行情，从2014年6月9日至2008年6月18日8个交易日内的中国石油股票的1 min高频交易数据，合计共1933个交易数据.如果每天中国石油的股票价格变动0.02元，即1 d内只要中国石油前后交易价格超过0.02元，我们就认为一次交易发生了.经过这样的截断后，得到511笔交易数据.然后利用Xi=ti－ti－1，对511笔计算交易之间交易的时间间隔，交易的时间间隔的均值是3.788 6 s，标准差3.953 4，最小值 1 min，最大值是 29 min.然后计算交易的时间间隔的自相关系数和偏相关系数:前二十阶自相关系数依次为1.0000，0.1275，－0.001 8，0.026 1，0.004 6，－ 0.020 7，0.075 2，0.093 9，0.023 3，－0.019 1，－0.032 9，－0.057 8，－ 0.022 8，0.002 8，－ 0.004 8，－ 0.063 3，－0.054 2，－0.042 2 0.082 7，0.041 0，－0.069 0，以及滞后15阶的Ljung-Box统计量为Ljung-Box(15)=630.696 6［3］.由 Engle 的 ACD 模型的定义，股票的交易持续期间的相互关系通过条件期望 ψi=E(xi|xi－1，…，x1)来完成刻化，其中 Ψi可表示为 Ψi－1和 xi－1的线性函数，通过检验“标准化”的持续期间εi=xi/Ψi的线性相关性，我们从模型的角度看数据是否具有聚集现象［4］.

由于自回归条件持续期(ACD)模型利用GARCH模型的思想，采用最简单的ACD(1，1)模型，因此利用 Matlab金融工具箱中的估计GARCH模型参数的方法估计式(1.21)中的参数ω，γ1，ω1.表1 是中国石油 ACD(1，1)模型的参数估计结果.

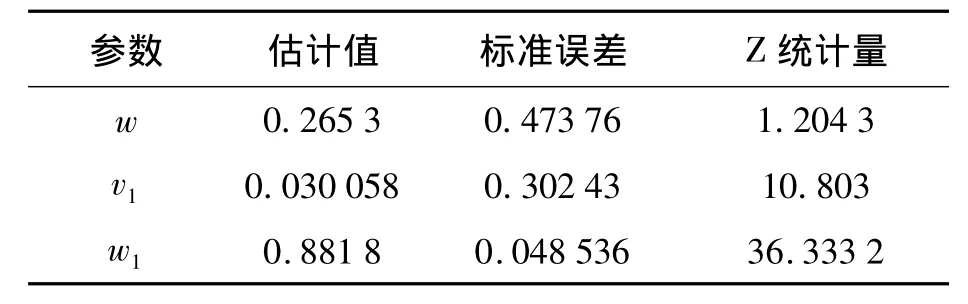
表1 中国石油ACD(1，1)模型的参数估计结果

因此，对(1.21)式的估计结果为 Ψi=0.265 3+0.03xi－1+0.881 8Ψi－1，之后，利用 ε′i=xi/Ψ′i求出标准持续期，图1和图2分别为调整持续期和标准持续期的时间图.图3和图4分别为调整持续期和标准持续期的自相关函数图.

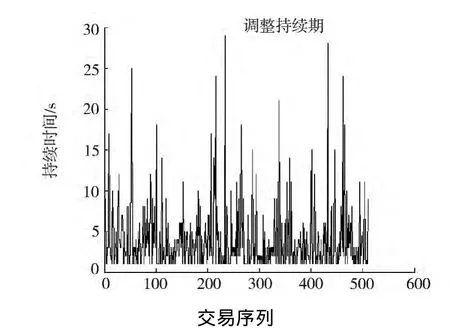
图1 调整持续期

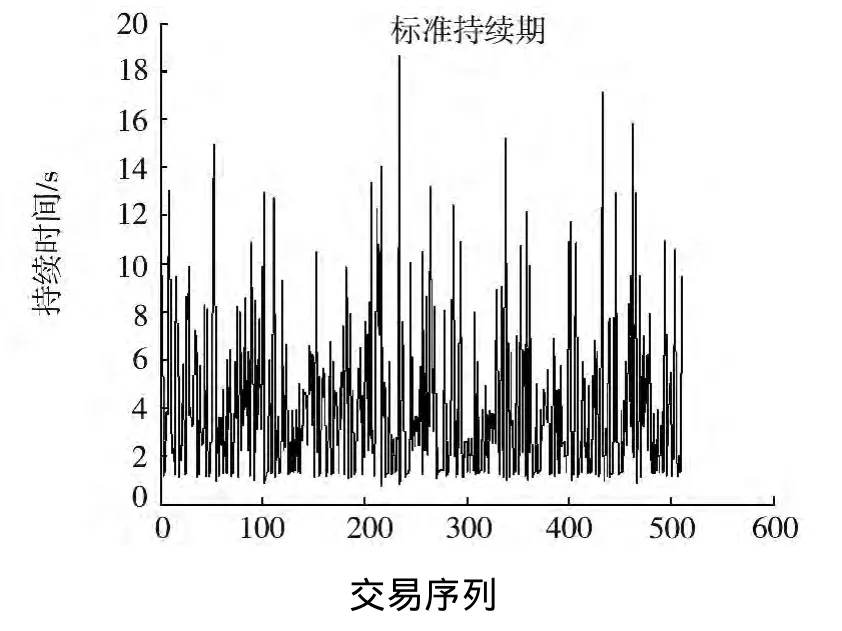
图2 标准持续期

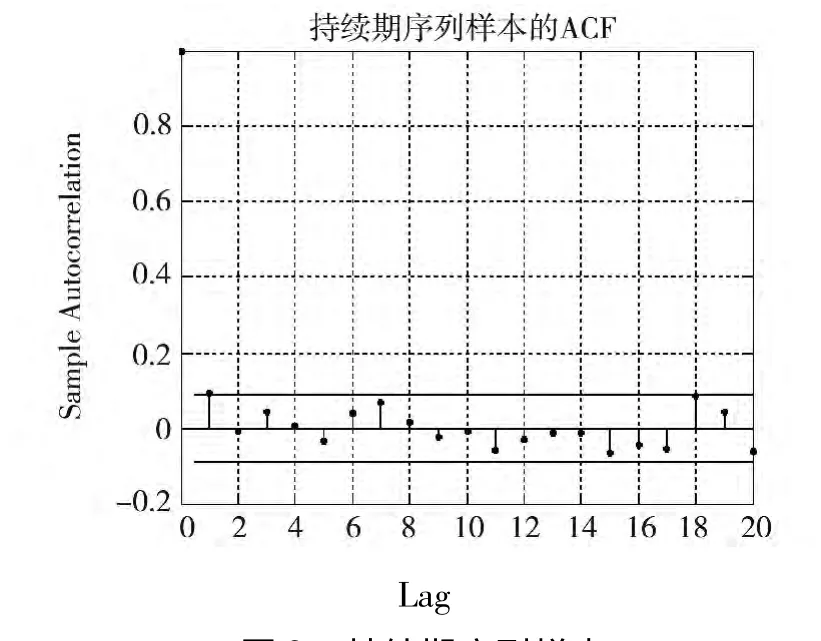
图3 持续期序列样本

图4 εi的样本ACF

通过检验“标准化”的持续期间 ε′i=xi/Ψ′i的自相关性，我们从模型的角度来看数据是否具有聚集现象.表2是中国石油波动率GARCH参数结果.

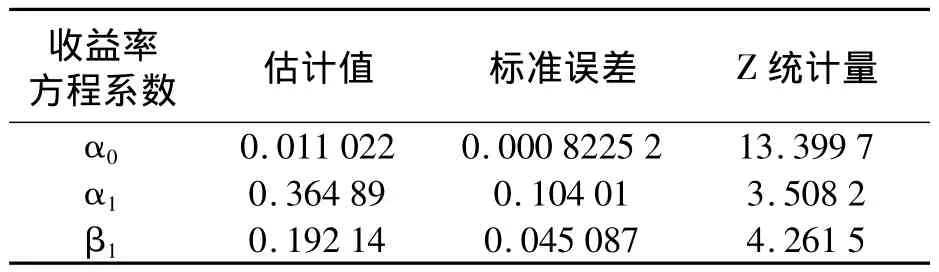
表2 中国石油的收益率GARCH(1，1)模型的参数估计结果

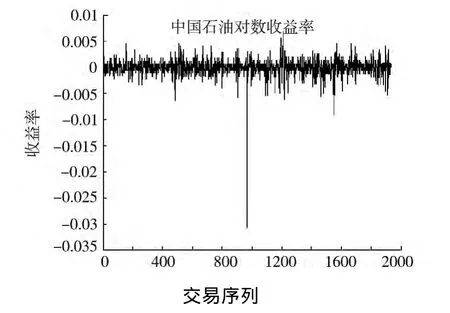
图5 对数收益率

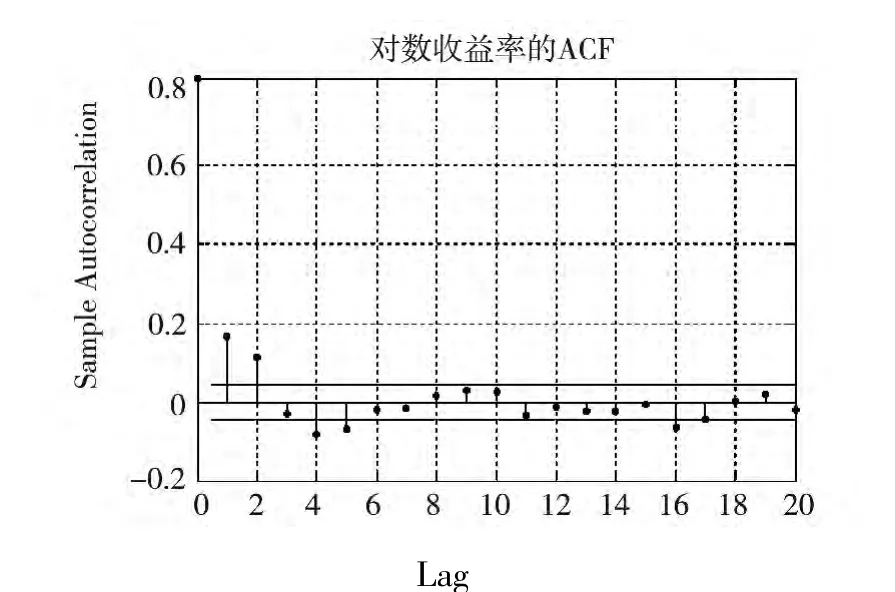
图6 对数收益率ACF

3 结 论

利用Ljung-Box统计量来检验与的相关性.在延迟l5阶的情况下，中石油持续期间 的相关性检验统计量的值为630.696 6，远远大于5%水平的临界值25，拒绝15阶自相关系数都为0的原假设，说明持续期间xi存在显著的自相关性.而在延迟15阶的情况下，中石油 的相关性检验统计量的值为573.614 7，同样大于5% 水平的临界值25，无法拒绝前15阶自相关系数都为0的原假设.这说明ACD模型很好地解释了交易持续期间的相互依赖现象［5］.说明我国股市中，明股票交易具有间歇性频繁、平淡，同时也验证了持续期模型在研究高频数据方面特性的合理性.

［1］ Ruey S.Tsay(著)，潘家柱(译).金融时间序列分析［M］.北京:机械工业出版社，2006.

［2］ 张小涛，祝涛.针对高频数据的中国股市磁吸效应研究［J］.重庆理工大学学报:自然科学，2014，28(1):123-127.

［3］ 屈博，魏平.基于高频数据的我国股票市场弱式有效性检验［J］.中国物价，2014(1):76-78.

［4］ 常宁，徐国祥.金融高频数据分析的现状与问题研究［J］.财经研究，2004，30(3):31-39.

［5］ 余臻，王苏生，李育补.基于高频数据的股指期货和ETF指数套利研究［J］.华北电力大学学报:社会科学版，2014(2):40-46.