基于GO 法和RCM 的惯性导航系统预测维修平台设计

江秀红，段富海，陈璞，金霞

(1.大连理工大学 传感测控研究所，辽宁 大连116024;2.沈阳航空航天大学 电子信息工程学院，辽宁 沈阳110136;3.中航工业西安飞行自动控制研究所，陕西 西安710065)

0 引言

在惯性导航系统(INS)的维护保障方面，目前我国仍以多、勤、细的传统维护方式为主，由此出现了“定时维修”的维修过剩和“事后维修”的巨大损失等问题。预测性维修通过多种手段对系统和部件进行监测、评估，预测系统失效时间，以便在故障发生前就开展适当的修复性维修活动。与被动维修和预防维修相比，主动的预测性维修可有效优化维修策略、降低维修时间、提高装备的可用度、降低系统的寿命周期费用［1］。

许多学者针对预测维修模型和预测维修策略进行了深入的研究。Jardine 等从故障诊断、故障预测的角度对基于状态的维修策略进行了分析［2］。李树广等利用粗糙集协调近似表示空间模型方法得出近似约简结果及预测与决策规则，为装备维修保障提供决策技术支持［3］。顾煜炯等结合运行参数、状态监测参数以及运行统计参数等实现了发电设备状态的“劣化度”模糊评估［4］。徐玉国等面向单部件电子系统，利用故障预测中的损伤标尺方法，在完美换件维修的假设下，以单位时间成本、平均使用可用度和平均效费比为目标，提出了一种预测维修决策优化模型［5］。Compare 等提出利用风险敏感粒子滤波器预测部件剩余寿命，以提高系统预测维修决策的精度和快速性［6］。Ivan 等则讨论了基于状态的预测维修一般流程，并提出根据系统和部件实时维修/更新效费比来制定维修策略［7］。

INS 是对可靠性有极高要求的复杂机电系统，各部件之间以及部件与系统之间相互作用、相互影响、关联性很强。系统的失效不仅与部件的逻辑组合有关，还与部件的失效顺序及系统先前的状态相关。但现有的预测维修决策大多集中于依靠单部件或系统总体的静态可靠性特征来决定维修时机。由于这些静态特征不受实际应用过程的影响，也不能区分不同部件特征变化对系统总体性能的影响，因而降低了维修策略的可信度。有些研究虽然基于复杂系统的多状态信息进行了维修决策的优化，但多数也没有考虑实时运行过程中单部件对系统或子系统可靠性的动态影响，或者仅按照简单的部件连接方式(如串联、并联、表决以及冷储备等)确定不同的维修策略，对具有强耦合关系的INS 来说，这些方法或模型在实际应用中都存在一定不足。

以可靠性为中心的维修(RCM)在当前可靠性工程领域中具有很高的认同度［8］，它根据设备的实际运行情况，采用先进的检测诊断技术、可靠性和寿命评估技术，运用逻辑决断分析法来确定所需的维修内容、类型和级别，达到维修优化的目的。

本文以RCM 思想为指导，提出基于GO 法的INS 预测维修综合分析平台设计方法。

1 预测维修平台的总体设计思路

损伤标尺是电子系统故障预测中的一种重要方法［9］。所谓损伤标尺是指针对一种或多种失效机理，以被监控产品相同的工艺过程制作出来，预期寿命比被监控对象短的产品。出于成本和失效机理复杂的考虑，目前的损伤标尺大多是针对系统中某些重要部件的特定失效机理，采用保险和预警装置来实现预测。但对复杂系统，不可能对系统的所有部件都建立损伤标尺，而且若被监控系统有了修复活动，则损伤标尺也失去了预警作用。

GO 法是美国军方为分析武器系统安全性和可靠性而提出并逐渐发展起来的一种可靠性分析与评估方法，对于有多状态、有时序、尤其是有实际物流(如气流、液流、电流)产生的复杂系统的可靠性分析尤其适合［10-11］。GO 法直接把系统流程图或原理图翻译成GO 图，通过操作符(代表具体的部件或逻辑关系)、信号流(代表具体的物流或逻辑上的进程)来描述具体部件的运行、相互关系和逻辑关系。

GO 图反映了系统的原貌并表达了系统各部件之间的物理关系和逻辑关系，操作符的状态值和状态概率对应了所代表部件的可靠性分布。若能通过部件的寿命分布模型，将系统寿命周期中受到的各种时间应力(部件在生产、运输、工作等过程中受到的各种环境应力和工作应力)融入到GO 图中，则相当于为系统建立了一个虚拟的“可靠性损伤标尺”。此标尺能自动计算出系统或部件实时的可靠度和残余寿命，当预测到系统可靠度低于设定阈值时，便可对相应部件提出维修或更新计划。图1是基于GO法和RCM 的惯导预测维修平台的工作流程。

图1 基于GO 法和RCM 的惯导预测维修平台工作流程Fig.1 Predictive maintenance workflow of INS based on GO methodology and RCM

部件的可靠度通过相应的寿命分布函数获得，而系统或子系统的可靠度则需运行GO 平台获得。时间应力每采样一次，GO 图中操作符的状态概率则更新一次。根据操作符的当前状态概率及操作符的概率计算公式，沿信号流方向，逐步计算各操作符的输出状态概率，即可获得系统的可靠性信息。两种情况下会根据维修大纲调整维修计划:一是某部件的残余寿命低于设定阈值，这时需将此部件列入维修计划;二是由于各部件的相互耦合作用，导致系统或子系统完成任务的成功概率低于设定阈值，这时应对引起这一失效事件的一系列相关部件进行综合评价，找出对失效影响最大的部件，列入维修计划。这样，随着时间应力的更新，预测维修平台对部件和系统的可靠性不断进行动态计算、评估，并根据设定的可靠性指标不断调整维修计划。

2 基于GO 法的可靠性分析模型

GO 法对系统复杂度不敏感，且能够解决一些故障树法无能为力的可靠性分析问题，目前已在核电、电网配电、轨道交通等高可靠性领域中得到成功应用［12-13］。GO 法的定量分析主要有状态组合算法和概率公式算法［14］。状态组合算法需列出操作符和输入信号的全部状态组合来计算联合概率，比较繁琐。概率公式算法通过引入信号流状态累积概率直接导出操作符的计算公式，大大简化了定量计算。基于概率公式的GO 法定量计算步骤如下:

步骤1 进行系统功能分析，确定系统中各部件的操作符类型，建立GO 图。

步骤2 确定GO 图中各操作符及输入信号的状态概率。

步骤3 按信号流序列对每个操作符，按其类型相应的计算公式进行计算，直至得到代表系统输出信号的状态概率。

步骤4 若系统中含有共有信号，则需对步骤3的结果进行修正，以获得更为精确的输出结果。

通过以上步骤即可实现系统可靠性的定量计算。下面利用GO 法进行INS 可靠性建模，图2是某捷联惯导系统(SINS)的简化逻辑框图。

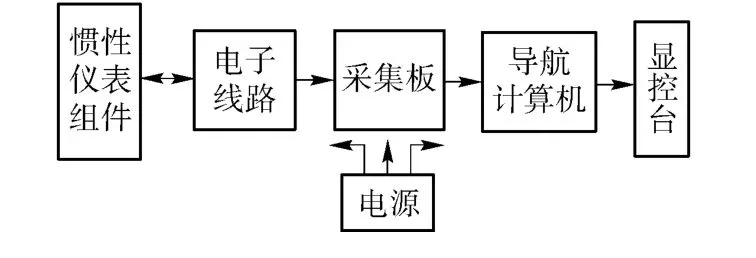
图2 某SINS 简化逻辑框图Fig.2 Simplified logical block diagram of some SINS

此SINS 包含如下部件:1)冗余配置的惯性仪表组件，包括4 个提供角速度的双轴陀螺和6 个提供比力的单轴加速度计;2)两套操纵惯性仪表的电子线路，每套内包含相同的底板、伺服板以及转位机构等;3)两套采集电路，用来采集惯性仪表输出数据，并按照导航计算机所需信号形式进行转换、传输;4)两台导航计算机，用来计算运载体的姿态、解算比力数据、求解导航方程式等;5)主备配置电源。根据系统的逻辑连接以及各部件的功能和GO 操作符的特点，将图2翻译成图3所示的GO 图，图中各操作符的数据如表1所示。

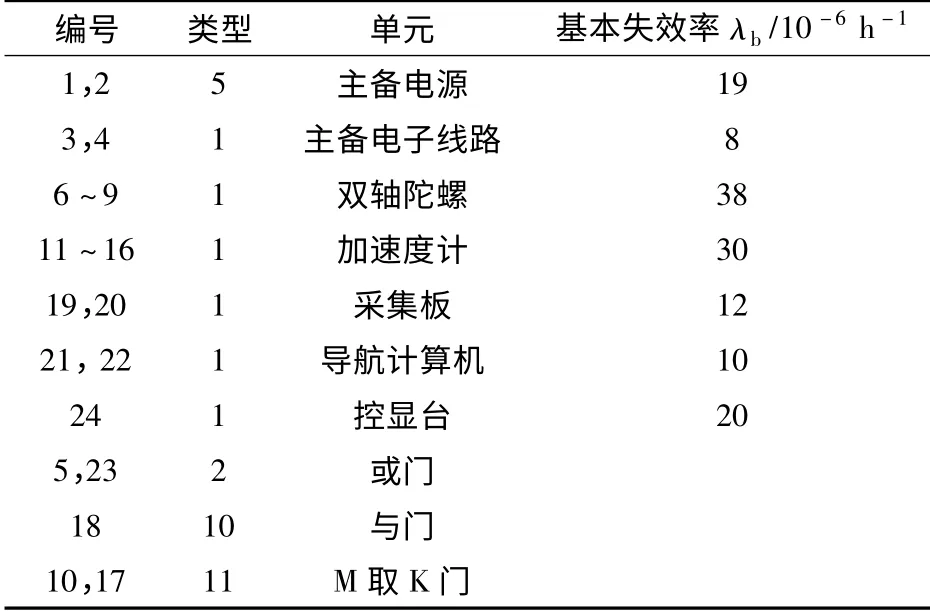
表1 SINS 操作符数据Tab.1 Operator data of SINS

图3 某SINS 的GO 图Fig.3 GO chart of some SINS

电源作为整个SINS 的驱动动力，是系统的唯一输入，因此用单信号发生器(类型5 操作符)代表。电子线路板、陀螺、加速度计、采集板以及导航计算机、控制显示台都设定为只有成功和故障两种状态的部件，用两状态单元(类型1 操作符)代表。只要正常工作的陀螺数不少于2 个，则陀螺组的输出信息就是完备的，所以用4 取2 门代表4个陀螺之间的关系，同样用6 取3 门模拟6 个加速度计之间的关系。陀螺和加速度计的输出均处于成功状态时，惯性仪表单元的输出才是有效的，因此用与门(类型10 操作符)代表之间的逻辑关系。电子线路板、导航计算机等都是冗余配置，所以用或门(类型2操作符)表示之间的逻辑连接。

状态值和状态概率是GO 图中操作符和信号流的两个属性。在两状态系统中，状态1 代表成功，状态2 代表故障，处于1 和2 的概率之和为1. 基于概率公式算法，下面给出图3中4 个主要信号流的计算公式，其中Pci、Psi分别表示操作符i 和信号流i 的成功概率，Fci、Fsi为对应的故障概率。

1)信号流5:Ps5=Pc1Pc3+Pc2Pc4-Pc1Pc2Pc3Pc4;2)信号流10:Ps10=［Pc6Pc7+Pc6Fc7(Pc8+Fc8Pc9)+Fc6Pc7(Pc8+Fc8Pc9)+Fc6Fc7Pc8Pc9］Ps5;3)信号流18:Ps18= Ps10+ Ps17- Ps10Ps17/Ps5;4)信号流24:Ps24=Ps18［Pc19Pc21+Pc20Pc22-Pc19Pc20Pc21Pc22］Pc24.

图3中信号流6 ～9，11 ～16 中均含有共有信号5. 对具有多个输入信号的某些操作符，如或门、与门、M 取K 门等，含有共有信号的多个输入之间不是完全独立的，直接计算可能带来较大误差，这时需对含共有信号的概率项进行修正［15］。本文采用降阶法，在输出信号的概率展开式中，直接将含共有信号的高次项用一次项替代，比如上面的信号流10、18 和24 的计算公式中都进行了降阶处理。

Ps24为控显台能成功输出飞行加速度及姿态角信息的概率。假设第k个采样时刻，部件i的可靠度为Ri(k)，则可令该部件对应操作符的成功和故障概率分别为Pkci=Ri(k)和Fkci=1 -Ri(k). 可见确定操作符状态概率的关键在于部件可靠度的计算。实际应用中，部件可靠度是由其内在特性和外部工作条件共同影响的，每个采样时刻对应的可靠度可能都不相同。下面根据部件的寿命分布函数以及概率论的基础知识，推导各个采样时刻对应的操作符状态概率。

3 操作符状态概率的迭代公式

3.1 操作符状态概率的确定

λ(t，x)表示部件失效率，x =(x1，x2，…，xk)，xi为第i 个时间应力。假设系统为均匀采样，初始运行时刻t =0，采样周期T0，则各采样时刻的失效率为

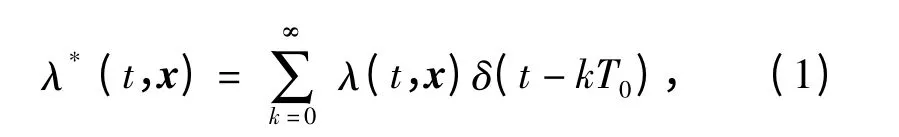
λ*(kT0，xk)为第k 个采样时刻部件的失效率。当t∈［kT0，(k+1)T0］时，假设部件失效率保持kT0时刻的值不变直到(k+1)T0时刻，则［kT0，(k+1)T0］区间部件的失效服从以λ*(kT0，xk)为参数的指数分布。当第k+1 个采样时刻到来时，新的时间应力采样值xk+1代入获得新的失效率，t∈［(k +1)T0，(k+2)T0］区间内，部件失效又开始服从以λ*((k+1)T0，xk+1)为参数的指数分布。随着工作时间t 的增长，部件的失效率不断更新，部件对应的可靠度也不断调整，到(k+1)T0时刻前部件的可靠度为

则(k+1)T0前部件不发生失效的概率可表示为

λ*(0，x0)可根据系统运行的历史记录给定，每进行一次采样则进行一次迭代，得到部件无故障工作到采样点前的可靠度，也即获得操作符的实时状态概率。

3.2 基于可靠度的残余寿命预测

假设某部件对应的安全可靠度阈值为R0，则部件可靠度降低为R0时对应的运行时间即为安全使用寿命。又失效率的高低可间接反映部件受到的累积损伤程度，则t∈［kT0，(k +1)T0］区间内，由于损伤造成的寿命变化量可表示为

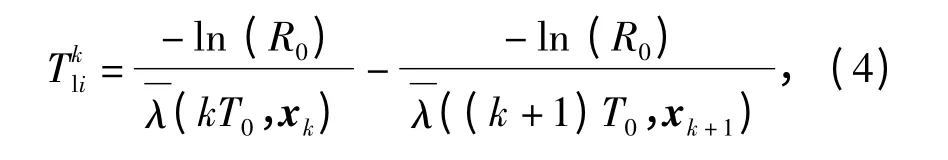
λ(kT0，xk)为kT0之前部件的平均失效率，(k+1)T0时刻部件i 的残余寿命Tk+1ri可表示为

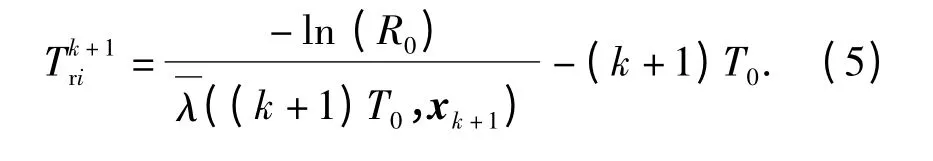
经采样后，部件失效近似服从分段指数分布，这样很容易估算出各个采样时刻前部件的可靠度以及各个采样时刻后部件的残余寿命。然后结合部件能够安全工作的可靠性指标，即可判断出哪些部件即将超过安全工作范围，以便及时给出维修或更新建议，调整维修计划。

4 系统可靠性的综合评价

当系统可靠度低于设定阈值时，需通过一定的评价方法将维修任务定位到具体的部件上。本文利用综合评价法，对可靠性不达标的系统进行评价，给出各个部件的维修优先度，以便为维修计划的调整提供支撑信息。

4.1 影响因素集

影响因素集合U ={u1，u2，…，un}表示影响维修定位的因素，C ={c1，c2，…，cm}表示系统所含部件对应操作符的集合，则U 与C 之间的评价矩阵V可表示为

式中:vij表示操作符ci在影响因素uj下的评估值。针对SINS，为简化评判过程，令U ={贡献度，失效频度，检测度}。贡献度表示部件对系统可靠度的影响程度。基于故障树分析中的概率重要度概念，将GO 图中的操作符看作“基本事件”，信号流看作具有不同成功准则的“顶事件”，也即用操作符状态概率变化引起系统可靠度变化的程度来衡量操作符对系统的重要度:

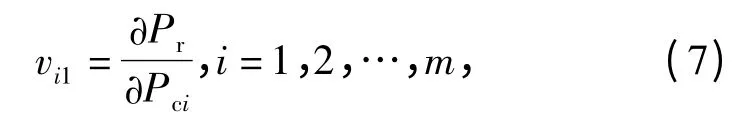
式中:Pr为系统的成功状态概率;Pci为操作符i 的成功状态概率。第k 个采样时刻的vki1可用如下公式近似估算:

式中:Pkr-1是系统在(k -1)T0时刻的成功概率;Pkri是从(k-1)T0到kT0，只考虑操作符i 状态概率变化时系统的成功概率(其余操作符保持kT0时刻的概率值不变);Pkci是操作符i 在kT0时刻的成功状态概率。

“失效频度”表明操作符自身发生失效的程度。kT0时刻操作符i 的可靠度为Pkci，部件的可靠度越低，发生失效的概率越高，则被选中进行维修的概率越高，所以可令vki2=1 -Pkci=Fkci.

“检测度”是部件的可检测性、维修费用以及维修难易度等影响因素的综合衡量值，可根据历史数据或专家经验模糊给定。最后对矩阵V 按列进行归一化处理，即可获得系统中所含操作符的评价矩阵。

4.2 综合评判矩阵

定义向量A=［a1，a2，…，an］，表示各影响因素在评估中所占的权重，则综合评判矩阵:

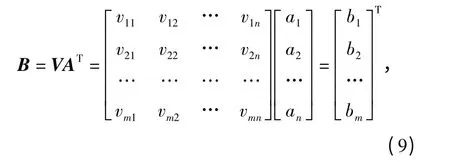
式中:bi表示综合考虑各影响因素U 后，操作符i 进行维修检查的优先度，bi越大，则操作符i 纳入维修的优先级越高，可根据bi的大小调整维修计划。

5 算例验证

为专注于验证所提预测维修平台的可行性和有效性，做如下假设和约束:1)前期工作已能提供高置信水平的部件寿命分布模型，且失效检测是完善的;2)以RCM 思想为指导提出预测维修计划，暂不考虑维修人员的可用性、维修部件的可用度以及可利用的维修地点和工具等因素;3)不区分工作时间和日历时间，忽略部件的维修和更新时间，将关注点聚焦于维修间隔。

通过Matlab 搭建SINS 的可靠性分析平台进行算法验证。分析前首先利用层次分析法确定U 中各影响因素在系统评估中所占的权重A. 参考专家意见构造3 个影响因素的判断矩阵:

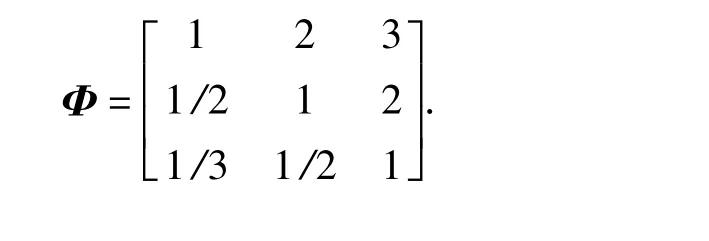
Φ 的最大实特征根及对应的特征向量分别为λmax=3.009，ξ=［0.847，0.466，0.256］T. 经一致性检验，一致性比率Rc≈0.008 ＜0.1，说明Φ 的一致性可以接受。最后对ξ 进行归一化处理，可得3 个影响因素的权重为A =［0.54，0.30，0.16］T. 下面分别按部件失效率恒定、失效率可变两种情况计算系统动态可靠度以及相应的维修决策制定。

5.1 失效率恒定

假定各部件安全使用范围均为Pc＞0.8，工作失效率与基本失效率λb(如表1)一致，采样时间T0=1 h，工作周期T =4 000 h，则部分部件和系统(以控显台输出有效为成功目标)的动态可靠度输出如图4所示。

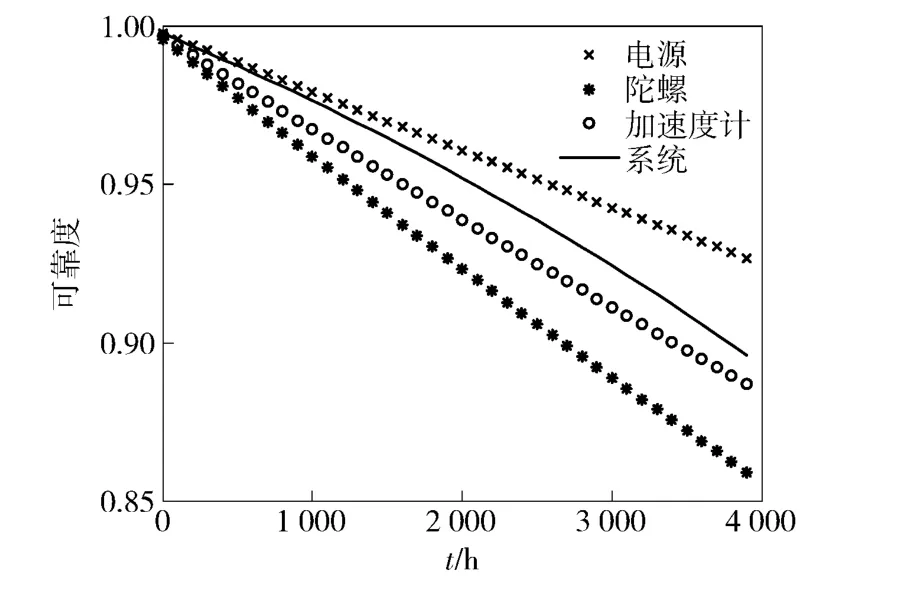
图4 部件和系统的动态可靠度(失效率恒定)Fig.4 Dynamic reliabilities of components and system(constant failure rate)

由图4可见，随着工作时间t 的增长，各部件以及系统的成功概率逐渐降低。当t≥488 h 时，系统可靠度Pr＜0.99;当t≥3 880 h 时，Pr则降低到0.90.

假设系统可靠度阈值为0.90，表2列出了t =3 880 h时各部件的影响因素评估值以及由(9)式计算出的部件维修优先度。

贡献度和失效频度是通过系统的动态仿真GO平台计算获得的，而检测度则是根据专家经验或历史统计数据人为给定的。表2最后一列给出了部件优先维修的量化结果，据此可对维修计划提出修改意见。假如按部件维修优先度的大小依次进行更新维修(维修后部件可靠度为1，且对于冗余部件只更换满足任务需求的最小数目部件，如4 个陀螺一次只更新2 个;6 个加速度计一次更新3 个)，则更新后系统的可靠度P'r如表3所示。维修人员可根据可靠性指标要求制定相应的维修计划，如为使维修后系统的可靠度不小于0.99，需将控显台、电源、陀螺、计算机均列入维修计划。

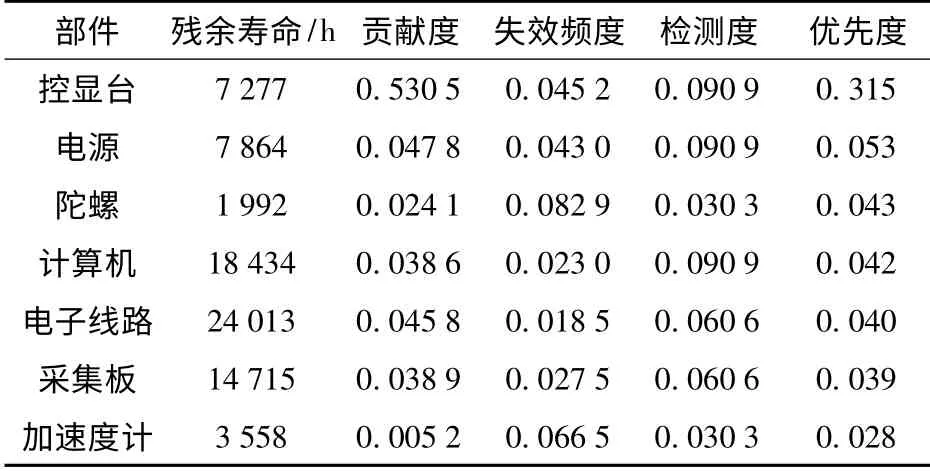
表2 部件维修优先度(t=3 880 h)Tab.2 Maintenance priorities of components (t=3 880 h)

也可基于部件维修优先度，通过建立维修的单位时间成本模型来优化维修计划。比如系统发生失效时，按部件维修优先度的大小依次扩大维修部件范围，若各部件的维修成本均为C0，系统每次维修的固定费用为2C0，维修后部件的可靠度为1(更新维修)，则预测维修评价结果如表3最后两列所示。

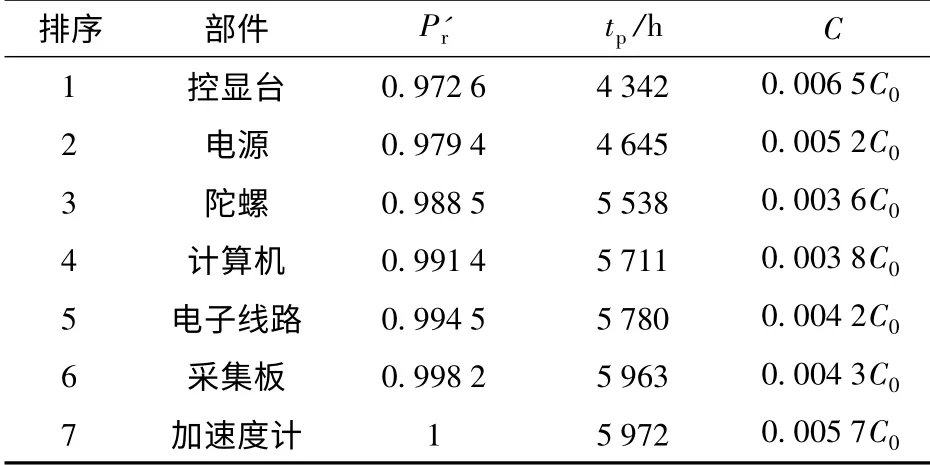
表3 t=3 880 h 时系统的预测维修评价结果Tab.3 Evaluation results of predictive maintenance(t=3 880 h)

表3中的tp为系统下一次维修时刻的预测值(系统可靠度低于0.90);C 为前后两次维修的单位时间成本。从表3可以看出，随着维修部件范围的扩大，维修所需的单位时间成本先降低后又逐渐升高，维修人员可以根据系统可靠性指标以及维修时间间隔灵活选定维修范围。比如若想获得最小的单位时间成本，可选择控显台、电源以及陀螺进行维修更换。

5.2 失效率可变

若各部件的失效率不是恒定的，如表4所示。表4中，πT为温度应力对电路失效率的调整系数，πV为电压应力对电路失效率的调整系数，πE为不同类别的环境应力(除温度应力外)对部件失效率影响的调整系数。某工作剖面中，各应力系数分布如图5所示。假设各部件承受的应力系数相同，则部件及系统的动态可靠性输出如图6所示。

表4 部件的失效分布Tab.4 Failure distribution of components

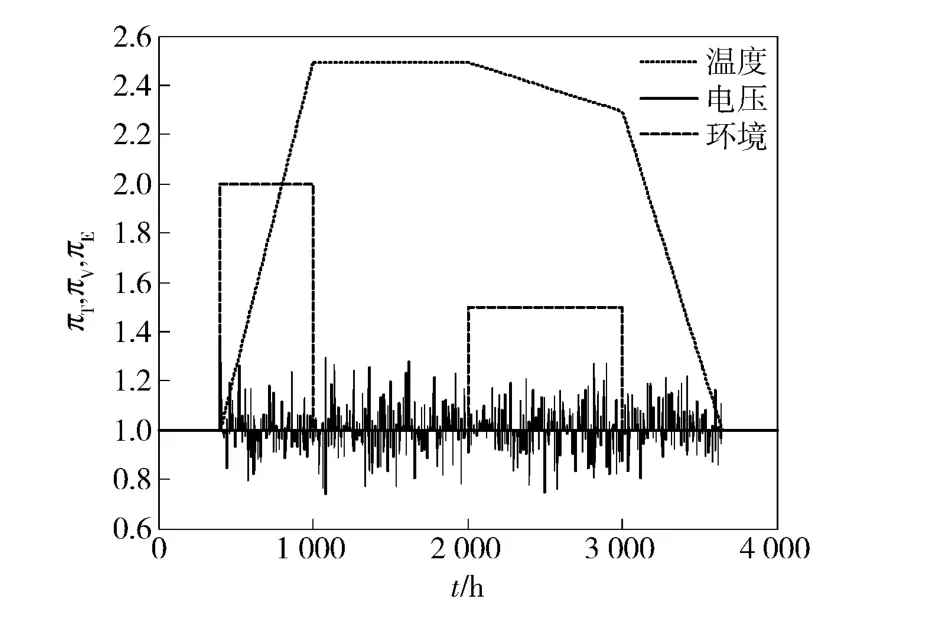
图5 应力系数的分布曲线Fig.5 Distribution curve of stress coefficient

当运行时间t≥2 753 h 时，系统可靠度Pr＜0.90. 表5给出了t=2 753 h 时部件的维修优先度。由于陀螺和加速计在工作时间t ＜2 754 h 之前就已超其安全工作范围，必须进行维修，所以优先度直接置为1，其余部件则仍按优先度的大小及系统维修后的可靠性指标进行选择性维修。

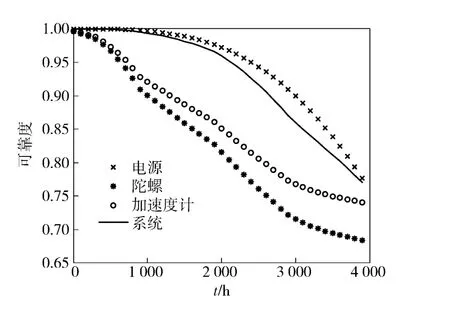
图6 部件和系统的动态可靠度(失效率可变)Fig.6 Dynamic reliabilities of components and system(variable failure rate)

5.3 故障部件隔离

一些突发性的状况可能会导致不符合统计规律的偶然故障发生，所以若预测维修平台能与基于状态监测的故障诊断系统配合使用，依据可靠性分析所得的宏观结论与状态监测系统所得的运行现状，就可对系统的健康状况做出更全面的评价。维修平台的评价结果可为故障的快速诊断提供支撑信息，反过来，故障诊断的结果又可用来调整部件的可靠度，提高预测维修平台的可信度。比如在运行过程中，若故障诊断系统判断出某部件出现故障，需进行隔离并退出工作状态，则只需在分析平台上将相应部件的可靠度置为0 即可(可根据故障的程度，将部件可靠度与一个［0 ～1］范围内的调整系数相乘)，图7是故障部件隔离后系统可靠度的动态输出曲线。

可见，由于预测维修平台是动态调整的，当某部件出现突发故障时，其可靠度的变化很容易在下一个采样时刻得到回应。因此维修平台仍能很好地反映系统的可靠性以及维修状况等。

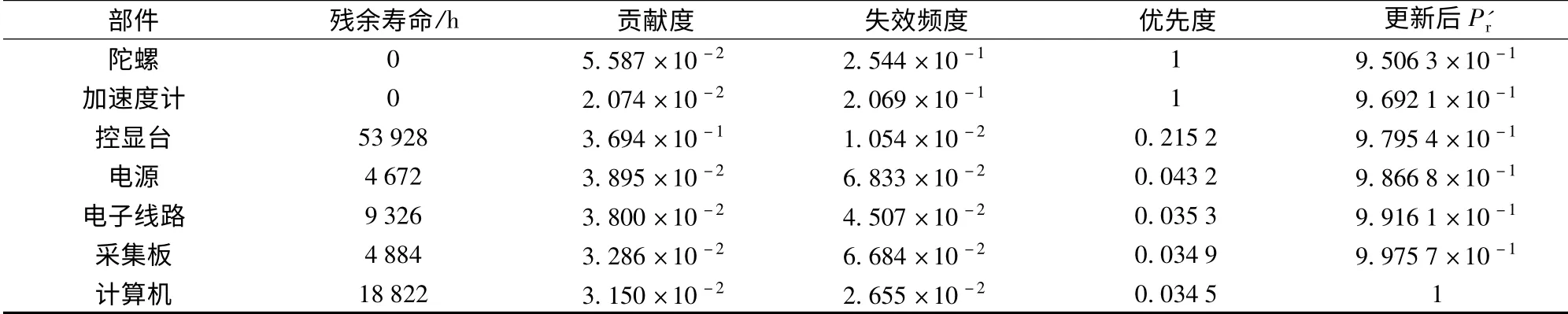
表5 部件维修优先度(t=2 753 h)Tab.5 Maintenance priorities of components (t=2 753 h)

6 结论

1)利用GO 法搭建了INS 的可靠性分析平台，并将寿命分布模型融入到可靠性平台中，形成了一个综合可靠性评估、残余寿命预测、维修预测为一体的管理平台。维修人员可根据部件的维修优先度、残余寿命以及部件更新后的系统可靠度，确定最佳的维修时机和维修项目。

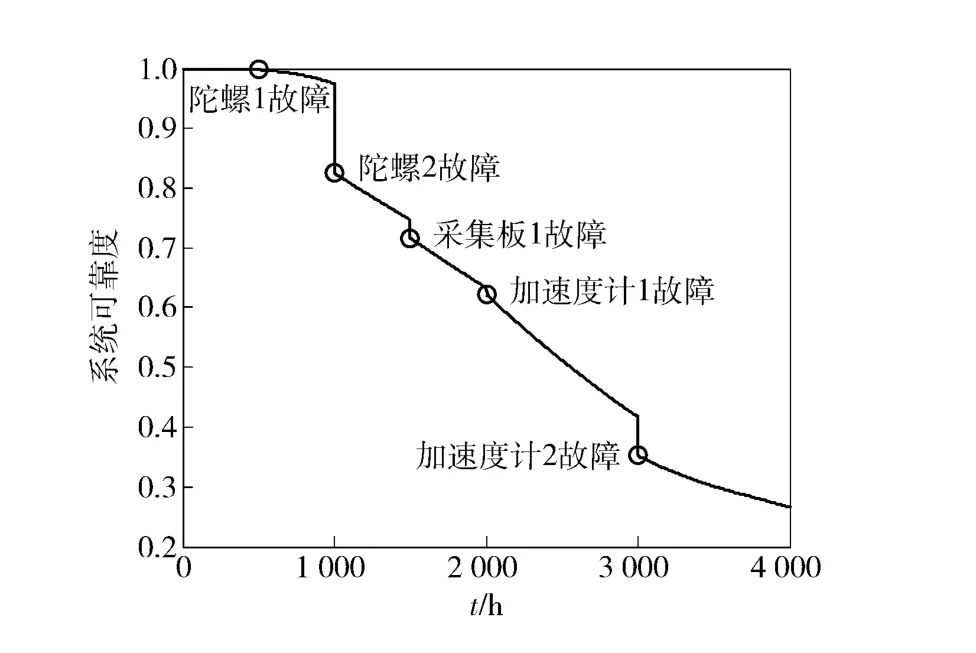
图7 故障部件隔离后系统的动态可靠度Fig.7 Dynamic reliability of system after isolating faulty components

2)随着时间的推移，系统的性能可能存在潜在变化。本文提出的虚拟“可靠性损伤标尺”，利用GO 操作符的灵活组合，与实际系统硬件配置和逻辑连接非常符合，并且通过数据的采样在运行方面保持与系统的同步，从而能连续准确地评估系统的性能，尽可能早地感知各种导致系统性能下降的故障，减少不必要的预防性维修，增加系统的运行时间和降低使用费用。

3)所得的维修评价结果既可为操作人员提供故障预警，也能在宏观上协助维修计划的制定。若与故障诊断、故障预测等平台相互配合使用，可实现INS 健康状况的全方位管理。

4)由于INS 可靠性评估所需相关数据的统计还不完善，在GO 法的分析过程中对INS 部分可靠性数据进行了经验假设，部件寿命分布模型的全面性和精确性也有待验证和提高。实际应用中，可通过可靠性试验或历史经验数据，建立部件的寿命分布模型，将可靠性与失效过程的环境、物理特点和使用剖面联系在一起，提高分析结果的可信度。

References)

［1］ Charles E E. 可靠性与维修性工程概论［M］. 康锐，李瑞莹，王乃超，等，译. 北京:清华大学出版社，2010:169 -190.Charles E Ebeling. An introduction to reliability and maintainability engineering［M］. KANG Rui，LI Rui-ying，WANG Nai-chao，et al，translated. Beijing:Tsinghua University Press，2010:169 -190. (in Chinese)

［2］ Jardine A K，Lin D，Banjevic D. A review on machinery diagnostics and prognostics implementing condition-based maintenance［J］. Mechanical Systems and Signal Processing，2006，20(7):1483 -1510.

［3］ 李树广，赵彦峻，徐诚，等. 装备维修备件需求预测与决策方法研究［J］. 兵工学报，2011，32(7):901 -905.LI Shu-guang，ZHAO Yan-jun，XU Cheng，et al. The study of requirement forecasting and decision-making methodology of equipment’s maintenance spares-parts［J］. Acta Armamentarii，2011，32(7):901 -905. (in Chinese)

［4］ 顾煜炯，董玉亮，杨昆. 基于模糊评判和RCM 分析的发电设备状态综合评价［J］. 中国电机工程学报，2004，24(6):189 -194.GU Yu-jiong，DONG Yu-liang，YANG Kun. Synthetic evaluation on conditions of equipment in power plant based on fuzzy judgment and RCM analysis［J］. Proceedings of the CSEE，2004，24(6):189 -194. (in Chinese)

［5］ 徐玉国，邱静，刘冠军，等. 基于损伤标尺的电子设备预测维修决策优化［J］. 航空学报，2012，33(11):2093 -2103.XU Yu-guo，QIU Jing，LIU Guan-jun，et al. Optimal predictive maintenance decision of electronics based on canaries［J］. Acts Aeronautics et Astronautics Sinica，2012，33(11):2093 -2103.(in Chinese)

［6］ Compare Michele，Zio Enrico. Risk sensitive particle filtering in support of predictive maintenance［J］. Chemical Engineering Transactions，2013，33:307 -312.

［7］ Ivan Mustakerov，Daniela Borissova. An intelligent approach to optimal predictive maintenance strategy defining［C］∥2013 IEEE International Symposium on Innovations in Intelligent Systems and Applications. Albena，Bulgaria:IEEE，2013.

［8］ William R W. Reliability engineering approach to achieve RCM for mechanical systems-2012［C］∥2012Annual Reliability and Maintainability Symposium. Reno，Nevada:Institute of Electrical and Electronics Engineers Inc，2012.

［9］ Vichare N M，Pecht M G. Prognostics and health management of electronics［J］. IEEE Transactions on Components and Packaging Technologies，2006，29(1):222 -229.

［10］ Chun B B. GO methodology:overview manual，EPRI NP-3123l［R］. Washington，DC，US:Electric Power Research Institute，1983.

［11］ 沈祖培，黄祥瑞. GO 法原理及应用——一种系统可靠性分析方法［M］. 北京:清华大学出版社，2004:169 -190.SHEN Zu-pei，HUANG Xiang-rui. Principle and application of GO methodology—a system reliability analysis methodology［M］. Beijing:Tsinghua University Press，2004:169-190. (in Chinese)

［12］ 李哲，鲁宗相，刘井泉. 基于GO 法的核电厂电气主接线系统可靠性分析［J］. 核动力工程，2010，31(3):69 -73.LI Zhe，LU Zong-xiang，LIU Jing-quan. Reliability analysis of nuclear power plant bus systems arrangement based on GO methodology［J］. Nuclear Power Engineering，2010，31(3):69 -73. (in Chinese)

［13］ 龚剑波，黄民翔，徐国锋. 基于改进GO 法的1 000 kV 电气主接线可靠性研究［J］. 机电工程，2012，29(2):215 -219.GONG Jian-bo，HUANG Min-xiang，XU Guo-feng. Reliability research of 1 000 kV main electrical connections based on improved GO methodology［J］. Journal Mechanical＆Electrical Engineering，2012，29(2):215 -219. (in Chinese)

［14］ Shen Z P，Gao J，Huang X R. A new quantification algorithm for the GO methodology［J］. Reliability Engineering and System Safety，2000，67(3):241 -247.

［15］ Shen Z P，Gao J，Huang X R. An exact algorithm dealing with shared signals in the GO methodology［J］. Reliability Engineering and System Safety，2001，73(2):177 -181.